Маслова Т.Н., Суходский А.М. Справочник школьника по математике. 5-11 кл
Подождите немного. Документ загружается.

ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
157156
Äëÿ ôóíêöèé
xy tg=
è
xy ctg=
ñïðàâåäëèâû
ðàâåíñòâà
.,ctg)ctg(,tg)tg( ZÎ=p+=p+ kxkxxkx
Òàêèì îáðàçîì, ëþáîå ÷èñëî âèäà
kp2
ÿâëÿåòñÿ
ïåðèîäîì ôóíêöèé
,cos,sin xx
à ÷èñëî âèäà
kp
ïåðèîäîì ôóíêöèé
.ctg,tg xx
Ïðè ýòîì
p2
îñ-
íîâíîé ïåðèîä
,cos,sin xx
à
p
îñíîâíîé ïåðèîä
xx ctg,tg
(ñì. ï. 96).
Èñïîëüçóÿ ñâîéñòâà ÷åòíîñòè, íå÷åòíîñòè, ïåðèî-
äè÷íîñòè, ìîæíî òðèãîíîìåòðè÷åñêóþ ôóíêöèþ èí-
òåðåñóþùåãî íàñ óãëà ñâåñòè ê òðèãîíîìåòðè÷åñêîé
ôóíêöèè óãëà, çàêëþ÷åííîãî â ïðåäåëàõ îò 0
° äî 180°.
Ï ð è ì å ð. Âû÷èñëèòü
.945sin °
q Èìååì sin 945
°
= sin (720
°
+ 225
°
) = sin (225
°
+
+ 360
°
· 2) = sin 225
°
= sin (225
°
360
°
) = sin (135
°
) =
= sin135
°
.
Äàëåå, sin 135
°
= sin (180
°
45
°
) = sin 45
°
(ñì. ï. 80), íî
2
2
45sin
=°
(ñì. ï. 118), çíà÷èò,
sin 945
°
= sin 135
°
= sin 45
°
= . n
122. Ñâîéñòâà è ãðàôèê ôóíêöèè
x.y sin=
1
0
. Îáëàñòü îïðåäåëåíèÿ ìíîæåñòâî R.
2
0
. Ìíîæåñòâî çíà÷åíèé îòðåçîê [1, 1].
3
0
. Ôóíêöèÿ ïåðèîäè÷åñêàÿ; îñíîâíîé ïåðèîä ðà-
âåí
p2 .
4
0
. Ôóíêöèÿ íå÷åòíàÿ.
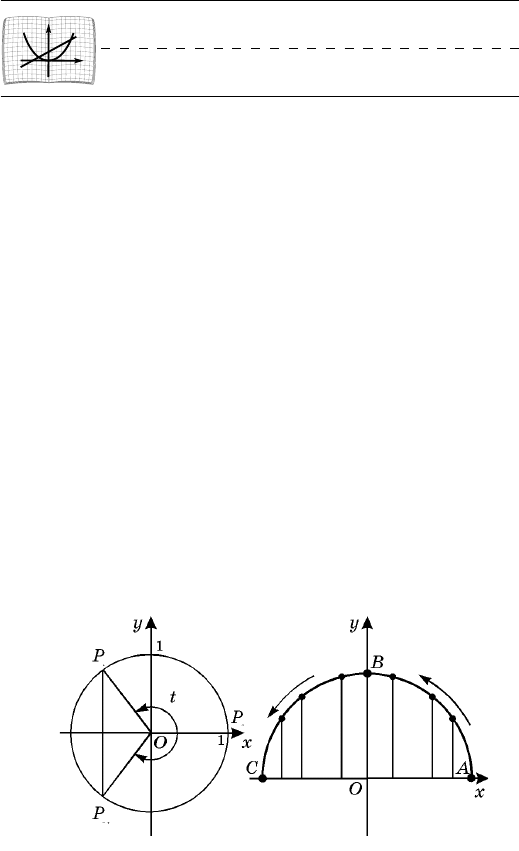
îêðóæíîñòè èìåþò îäèíàêîâóþ àáñöèññó è ïðîòèâî-
ïîëîæíûå (îòëè÷àþùèåñÿ äðóã îò äðóãà ëèøü çíà-
êîì) îðäèíàòû (ðèñ. 46). Ýòî çíà÷èò, ÷òî cos (t) =
,cos t=
sin (t) = sin t, ò. å.
xy
cos
=
÷åòíàÿ, à
y = sin x íå÷åòíàÿ ôóíêöèÿ. Ôóíêöèè y = tg x,
xy ctg=
íå÷åòíûå.
121. Ïåðèîäè÷íîñòü òðèãîíîìåòðè÷åñêèõ ôóíêöèé.
Òàê êàê Ð
t
è Ð
t + 360°
îäíà è òà æå òî÷êà åäèíè÷íîé
îêðóæíîñòè (ñì. ï. 118), òî ñèíóñû ñîîòâåòñòâóþùèõ
óãëîâ, à òàêæå èõ êîñèíóñû ðàâíû. Çíà÷èò,
sin (x + 360
°
) = sin x, cos (x + 360
°
) = cos x,
Áîëåå îáùèìè ÿâëÿþòñÿ ðàâåíñòâà
sin (x + 360
°
k) = sin x, cos (x + 360
°
k) = cos x,
ãäå k ëþáîå öåëîå ÷èñëî.
Åñëè àðãóìåíò õ âûðàæåí â ðàäèàíàõ, òî
sin (x + 2pk) = sin x, cos (x + 2pk) = cos x, k Î Z.
Ö2
2
t
0
t
Ðèñ. 47
Ðèñ. 46

ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
157156
Äëÿ ôóíêöèé
xy tg=
è
xy ctg=
ñïðàâåäëèâû
ðàâåíñòâà
.,ctg)ctg(,tg)tg( ZÎ=p+=p+ kxkxxkx
Òàêèì îáðàçîì, ëþáîå ÷èñëî âèäà
kp2
ÿâëÿåòñÿ
ïåðèîäîì ôóíêöèé
,cos,sin xx
à ÷èñëî âèäà
kp
ïåðèîäîì ôóíêöèé
.ctg,tg xx
Ïðè ýòîì
p2
îñ-
íîâíîé ïåðèîä
,cos,sin xx
à
p
îñíîâíîé ïåðèîä
xx ctg,tg
(ñì. ï. 96).
Èñïîëüçóÿ ñâîéñòâà ÷åòíîñòè, íå÷åòíîñòè, ïåðèî-
äè÷íîñòè, ìîæíî òðèãîíîìåòðè÷åñêóþ ôóíêöèþ èí-
òåðåñóþùåãî íàñ óãëà ñâåñòè ê òðèãîíîìåòðè÷åñêîé
ôóíêöèè óãëà, çàêëþ÷åííîãî â ïðåäåëàõ îò 0
° äî 180°.
Ï ð è ì å ð. Âû÷èñëèòü
.945sin °
q Èìååì sin 945
°
= sin (720
°
+ 225
°
) = sin (225
°
+
+ 360
°
· 2) = sin 225
°
= sin (225
°
360
°
) = sin (135
°
) =
= sin135
°
.
Äàëåå, sin 135
°
= sin (180
°
45
°
) = sin 45
°
(ñì. ï. 80), íî
2
2
45sin
=°
(ñì. ï. 118), çíà÷èò,
sin 945
°
= sin 135
°
= sin 45
°
= . n
122. Ñâîéñòâà è ãðàôèê ôóíêöèè
x.y sin=
1
0
. Îáëàñòü îïðåäåëåíèÿ ìíîæåñòâî R.
2
0
. Ìíîæåñòâî çíà÷åíèé îòðåçîê [1, 1].
3
0
. Ôóíêöèÿ ïåðèîäè÷åñêàÿ; îñíîâíîé ïåðèîä ðà-
âåí
p2 .
4
0
. Ôóíêöèÿ íå÷åòíàÿ.
îêðóæíîñòè èìåþò îäèíàêîâóþ àáñöèññó è ïðîòèâî-
ïîëîæíûå (îòëè÷àþùèåñÿ äðóã îò äðóãà ëèøü çíà-
êîì) îðäèíàòû (ðèñ. 46). Ýòî çíà÷èò, ÷òî cos (t) =
,cos t=
sin (t) = sin t, ò. å.
xy
cos
=
÷åòíàÿ, à
y = sin x íå÷åòíàÿ ôóíêöèÿ. Ôóíêöèè y = tg x,
xy ctg=
íå÷åòíûå.
121. Ïåðèîäè÷íîñòü òðèãîíîìåòðè÷åñêèõ ôóíêöèé.
Òàê êàê Ð
t
è Ð
t + 360°
îäíà è òà æå òî÷êà åäèíè÷íîé
îêðóæíîñòè (ñì. ï. 118), òî ñèíóñû ñîîòâåòñòâóþùèõ
óãëîâ, à òàêæå èõ êîñèíóñû ðàâíû. Çíà÷èò,
sin (x + 360
°
) = sin x, cos (x + 360
°
) = cos x,
Áîëåå îáùèìè ÿâëÿþòñÿ ðàâåíñòâà
sin (x + 360
°
k) = sin x, cos (x + 360
°
k) = cos x,
ãäå k ëþáîå öåëîå ÷èñëî.
Åñëè àðãóìåíò õ âûðàæåí â ðàäèàíàõ, òî
sin (x + 2pk) = sin x, cos (x + 2pk) = cos x, k Î Z.
Ö2
2
t
0
t
Ðèñ. 47
Ðèñ. 46
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
159158
íî èññëåäîâàíèþ ôóíêöèè
xy sin=
(ñì. ï. 122). Ïå-
ðå÷èñëèì ñâîéñòâà ôóíêöèè
:cos
xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ ìíîæåñòâî R.
2
0
. Ìíîæåñòâî çíà÷åíèé îòðåçîê [1, 1].
3
0
. Ôóíêöèÿ ïåðèîäè÷åñêàÿ ñ îñíîâíûì ïåðèî-
äîì
.2p
4
0
. Ôóíêöèÿ ÷åòíàÿ.
5
0
. Ôóíêöèÿ óáûâàåò íà ïðîìåæóòêàõ
+pp ,2[ n
]2 np+
è âîçðàñòàåò íà ïðîìåæóòêàõ
,]2,2[ nn pp+p-
.ZÎn
Ãðàôèê ôóíêöèè
xy
cos
=
èçîáðàæåí íà ðèñ. 49.
124. Ñâîéñòâà è ãðàôèê ôóíêöèè y = tg x.
1
0
. Îáëàñòü îïðåäåëåíèÿ:
.,
2
ZÎp+
p
¹ kkx
2
0
. Ìíîæåñòâî çíà÷åíèé âñÿ ÷èñëîâàÿ ïðÿ-
ìàÿ.
3
0
. Ôóíêöèÿ ïåðèîäè÷åñêàÿ ñ îñíîâíûì ïåðèî-
äîì
.
p
5
0
. Ôóíêöèÿ âîçðàñòàåò íà ïðîìåæóòêàõ
ú
û
ù
ê
ë
é
p+
p
p+
p
- nn 2
2
,2
2
è óáûâàåò íà ïðîìåæóòêàõ
ZÎ
ú
û
ù
ê
ë
é
p+
p
p+
p
nnn ,2
2
3
,2
2
(ðèñ. 47).
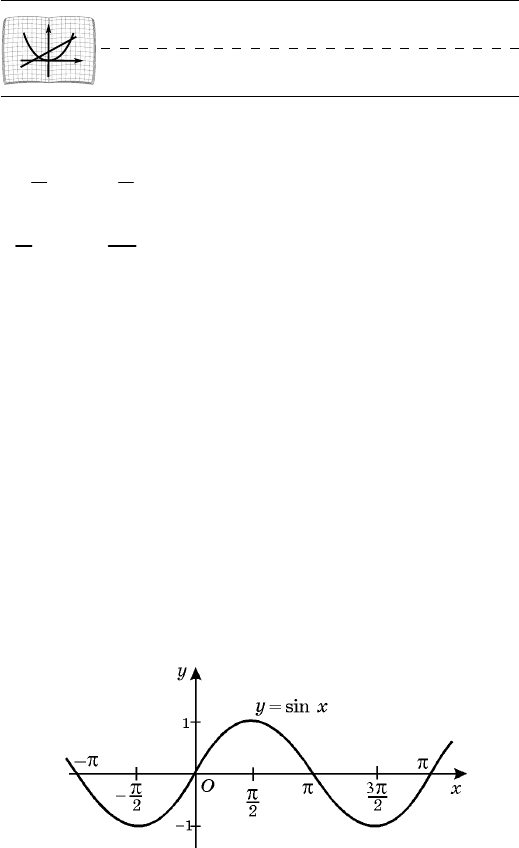
Âçÿâ êîíòðîëüíûå òî÷êè (0; 0),
),2/1;6/(p
),1;2/(p
),0;(p
ïîñòðîèì ãðàôèê ôóíêöèè
xy sin=
íà îòðåçêå
],0[ p
. Òàê êàê ôóíêöèÿ
xy sin=
íå÷åòíàÿ,
òî, îòîáðàçèâ ïîñòðîåííûé ãðàôèê ñèììåòðè÷íî îòíî-
ñèòåëüíî íà÷àëà êîîðäèíàò, ïîëó÷èì ãðàôèê ôóíê-
öèè íà îòðåçêå
],[ pp-
. Íàêîíåö, âîñïîëüçîâàâøèñü
ïåðèîäè÷íîñòüþ ôóíêöèè
xy sin=
, ìîæíî ïîñòðîèòü
ãðàôèê íà âñåé îáëàñòè îïðåäåëåíèÿ (ðèñ. 48).
123. Ñâîéñòâà è ãðàôèê ôóíêöèè
x.y cos=
Èñ-
ñëåäîâàíèå ôóíêöèè
xy cos=
ïðîâîäèòñÿ àíàëîãè÷-
Ðèñ. 49Ðèñ. 48

ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
159158
íî èññëåäîâàíèþ ôóíêöèè
xy sin=
(ñì. ï. 122). Ïå-
ðå÷èñëèì ñâîéñòâà ôóíêöèè
:cos
xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ ìíîæåñòâî R.
2
0
. Ìíîæåñòâî çíà÷åíèé îòðåçîê [1, 1].
3
0
. Ôóíêöèÿ ïåðèîäè÷åñêàÿ ñ îñíîâíûì ïåðèî-
äîì
.2p
4
0
. Ôóíêöèÿ ÷åòíàÿ.
5
0
. Ôóíêöèÿ óáûâàåò íà ïðîìåæóòêàõ
+pp ,2[ n
]2 np+
è âîçðàñòàåò íà ïðîìåæóòêàõ
,]2,2[ nn pp+p-
.ZÎn
Ãðàôèê ôóíêöèè
xy
cos
=
èçîáðàæåí íà ðèñ. 49.
124. Ñâîéñòâà è ãðàôèê ôóíêöèè y = tg x.
1
0
. Îáëàñòü îïðåäåëåíèÿ:
.,
2
ZÎp+
p
¹ kkx
2
0
. Ìíîæåñòâî çíà÷åíèé âñÿ ÷èñëîâàÿ ïðÿ-
ìàÿ.
3
0
. Ôóíêöèÿ ïåðèîäè÷åñêàÿ ñ îñíîâíûì ïåðèî-
äîì
.
p
5
0
. Ôóíêöèÿ âîçðàñòàåò íà ïðîìåæóòêàõ
ú
û
ù
ê
ë
é
p+
p
p+
p
- nn 2
2
,2
2
è óáûâàåò íà ïðîìåæóòêàõ
ZÎ
ú
û
ù
ê
ë
é
p+
p
p+
p
nnn ,2
2
3
,2
2
(ðèñ. 47).
Âçÿâ êîíòðîëüíûå òî÷êè (0; 0),
),2/1;6/(p
),1;2/(p
),0;(p
ïîñòðîèì ãðàôèê ôóíêöèè
xy sin=
íà îòðåçêå
],0[ p
. Òàê êàê ôóíêöèÿ
xy sin=
íå÷åòíàÿ,
òî, îòîáðàçèâ ïîñòðîåííûé ãðàôèê ñèììåòðè÷íî îòíî-
ñèòåëüíî íà÷àëà êîîðäèíàò, ïîëó÷èì ãðàôèê ôóíê-
öèè íà îòðåçêå
],[ pp-
. Íàêîíåö, âîñïîëüçîâàâøèñü
ïåðèîäè÷íîñòüþ ôóíêöèè
xy sin=
, ìîæíî ïîñòðîèòü
ãðàôèê íà âñåé îáëàñòè îïðåäåëåíèÿ (ðèñ. 48).
123. Ñâîéñòâà è ãðàôèê ôóíêöèè
x.y cos=
Èñ-
ñëåäîâàíèå ôóíêöèè
xy cos=
ïðîâîäèòñÿ àíàëîãè÷-
Ðèñ. 49Ðèñ. 48
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
161160
125. Ñâîéñòâà è ãðàôèê ôóíêöèè y = ctg x.
1
0
. Îáëàñòü îïðåäåëåíèÿ:
., ZÎp¹ kkx
2
0
. Ìíîæåñòâî çíà÷åíèé âñÿ ÷èñëîâàÿ ïðÿ-
ìàÿ.
3
0
. Ôóíêöèÿ ïåðèîäè÷åñêàÿ ñ îñíîâíûì ïåðèî-
äîì
.p
4
0
. Ôóíêöèÿ íå÷åòíàÿ.
5
0
. Ôóíêöèÿ óáûâàåò íà ïðîìåæóòêàõ
),,( kk p+pp
.ZÎk
6
0
. Ïðÿìûå
ZÎp= kkx ,
âåðòèêàëüíûå àñèìï-
òîòû.
Ãðàôèê ôóíêöèè
xy ctg=
èçîáðàæåí íà ðèñ. 51.
126. Ôóíêöèÿ y = arcsin x. Ôóíêöèÿ
xy sin=
âîçðàñòàåò íà îòðåçêå [p/2, p/2] ïðèíèìàåò íà íåì
4
0
. Ôóíêöèÿ íå÷åòíàÿ.
5
0
. Ôóíêöèÿ âîçðàñòàåò íà ïðîìåæóòêàõ
ç
è
æ
p+
p
- ,
2
k
.,
2
ZÎ
÷
ø
ö
p+
p
kk
6
0
. Ïðÿìûå
ZÎp+
p
= kkx ,
2
âåðòèêàëüíûå
àñèìïòîòû.
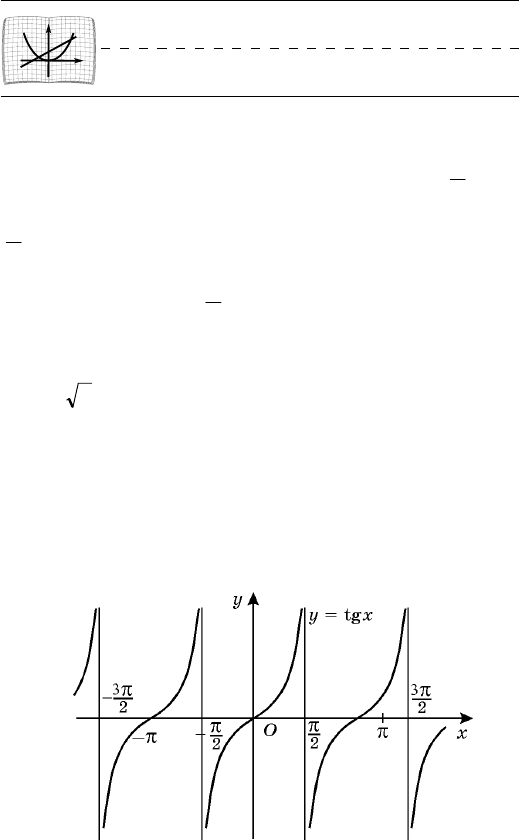
Âûáðàâ êîíòðîëüíûå òî÷êè (0; 0),
),1;4/(p
),3;3/(p
ñòðîèì ãðàôèê ôóíêöèè
xy tg=
íà ïðî-
ìåæóòêå
).2/,0[ p
Äàëåå, èñïîëüçóÿ íå÷åòíîñòü ôóí-
êöèè
xy tg=
, ïîñòðîèì ãðàôèê â èíòåðâàëå
).2/,2/( pp-
Íàêîíåö, âîñïîëüçîâàâøèñü ïåðèîäè÷-
íîñòüþ ôóíêöèè
xy tg=
, ïîñòðîèì ãðàôèê íà âñåé
îáëàñòè îïðåäåëåíèÿ (ðèñ. 50).
Ðèñ. 51Ðèñ. 50

ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
161160
125. Ñâîéñòâà è ãðàôèê ôóíêöèè y = ctg x.
1
0
. Îáëàñòü îïðåäåëåíèÿ:
., ZÎp¹ kkx
2
0
. Ìíîæåñòâî çíà÷åíèé âñÿ ÷èñëîâàÿ ïðÿ-
ìàÿ.
3
0
. Ôóíêöèÿ ïåðèîäè÷åñêàÿ ñ îñíîâíûì ïåðèî-
äîì
.p
4
0
. Ôóíêöèÿ íå÷åòíàÿ.
5
0
. Ôóíêöèÿ óáûâàåò íà ïðîìåæóòêàõ
),,( kk p+pp
.ZÎk
6
0
. Ïðÿìûå
ZÎp= kkx ,
âåðòèêàëüíûå àñèìï-
òîòû.
Ãðàôèê ôóíêöèè
xy ctg=
èçîáðàæåí íà ðèñ. 51.
126. Ôóíêöèÿ y = arcsin x. Ôóíêöèÿ
xy sin=
âîçðàñòàåò íà îòðåçêå [p/2, p/2] ïðèíèìàåò íà íåì
4
0
. Ôóíêöèÿ íå÷åòíàÿ.
5
0
. Ôóíêöèÿ âîçðàñòàåò íà ïðîìåæóòêàõ
ç
è
æ
p+
p
- ,
2
k
.,
2
ZÎ
÷
ø
ö
p+
p
kk
6
0
. Ïðÿìûå
ZÎp+
p
= kkx ,
2
âåðòèêàëüíûå
àñèìïòîòû.
Âûáðàâ êîíòðîëüíûå òî÷êè (0; 0),
),1;4/(p
),3;3/(p
ñòðîèì ãðàôèê ôóíêöèè
xy tg=
íà ïðî-
ìåæóòêå
).2/,0[ p
Äàëåå, èñïîëüçóÿ íå÷åòíîñòü ôóí-
êöèè
xy tg=
, ïîñòðîèì ãðàôèê â èíòåðâàëå
).2/,2/( pp-
Íàêîíåö, âîñïîëüçîâàâøèñü ïåðèîäè÷-
íîñòüþ ôóíêöèè
xy tg=
, ïîñòðîèì ãðàôèê íà âñåé
îáëàñòè îïðåäåëåíèÿ (ðèñ. 50).
Ðèñ. 51Ðèñ. 50
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
163162
Èç ñêàçàííîãî âûøå ñëåäóåò, ÷òî çàïèñè
xy arcsin=
è
yx sin=
,
,2/2/ p££p- y
ýêâèâàëåíò-
íû. Ïîäñòàâèâ â ðàâåíñòâî
yx sin=
âìåñòî ó åãî âû-
ðàæåíèå, ò. å.
,arcsin x
ïîëó÷èì
)(arcsinsin xx =
.
Ñëåäîâàòåëüíî, äëÿ ëþáîãî õ èç [1, 1] èìååì
.2/arcsin2/,)(arcsinsin p££p-= xxx
127. Ôóíêöèÿ y = arccos x. Ôóíêöèÿ
xy
cos
=
óáûâàåò íà îòðåçêå [0, p], ïðèíèìàåò íà íåì âñå çíà-
÷åíèÿ îò 1 äî 1 (ñì. ðèñ. 49). Çíà÷èò, äëÿ ôóíêöèè
xy
cos
=
, ðàññìàòðèâàåìîé íà îòðåçêå [0, p], ñóùåñòâó-
åò îáðàòíàÿ ôóíêöèÿ. Îíà îáîçíà÷àåòñÿ
xy
arccos
=
(÷èòàåòñÿ: «àðêêîñèíóñ õ»).
Ãðàôèê ôóíêöèè
xy
arccos
=
ïîëó÷àåòñÿ èç ãðà-
ôèêà ôóíêöèè
xy
cos
=
,
,0 p££ x
ñ ïîìîùüþ ïðå-
îáðàçîâàíèÿ ñèììåòðèè îòíîñèòåëüíî ïðÿìîé ó = õ
(ðèñ. 53).
Ïåðå÷èñëèì ñâîéñòâà ôóíêöèè
:arccos
xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ îòðåçîê [1, 1].
2
0
. Ìíîæåñòâî çíà÷åíèé îòðåçîê [0, p].
3
0
. Ôóíêöèÿ íå ÿâëÿåòñÿ íè ÷åòíîé, íè íå÷åòíîé.
4
0
. Ôóíêöèÿ óáûâàþùàÿ.
Èç ñêàçàííîãî âûøå ñëåäóåò, ÷òî çàïèñè
=y
xarccos=
è
,0,cos p££= yyx
ýêâèâàëåíòíû. Ïîä-
ñòàâèâ â ðàâåíñòâî
yx
cos
=
âìåñòî ó âûðàæåíèå
,arccos
x
ïîëó÷èì
xx =)(arccoscos
. Ñëåäîâàòåëüíî,
äëÿ ëþáîãî õ èç ïðîìåæóòêà [1, 1] èìååì
.arccos0,)(arccoscos p££= xxx
âñå çíà÷åíèÿ îò 1 äî 1 (ñì. ðèñ. 48). Çíà÷èò, äëÿ
ôóíêöèè
xy sin=
,
,2/2/ p££p- x
ñóùåñòâóåò îá-
ðàòíàÿ ôóíêöèÿ (ñì. ï. 115). Ýòó ôóíêöèþ îáîçíà-
÷àþò
xy arcsin=
(÷èòàåòñÿ: «àðêñèíóñ õ»).
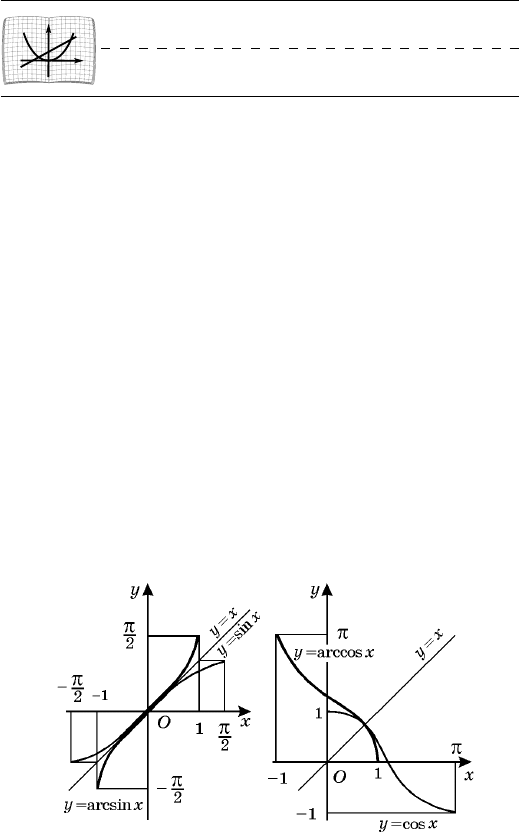
Ãðàôèê ôóíêöèè
xy arcsin=
ìîæíî ïîëó÷èòü èç
ãðàôèêà ôóíêöèè
xy sin=
,
,2/2/ p££p- x
ñ ïîìî-
ùüþ ïðåîáðàçîâàíèÿ ñèììåòðèè ïîñëåäíåãî îòíîñè-
òåëüíî ïðÿìîé ó = õ (ðèñ. 52).
Ïåðå÷èñëèì ñâîéñòâà ôóíêöèè
xy arcsin=
:
1
0
. Îáëàñòü îïðåäåëåíèÿ îòðåçîê [1, 1].
2
0
. Ìíîæåñòâî çíà÷åíèé îòðåçîê
].2/,2/[ pp-
3
0
. Ôóíêöèÿ íå÷åòíàÿ:
.arcsin)(arcsin xx -=-
4
0
. Ôóíêöèÿ âîçðàñòàþùàÿ.
Ðèñ. 52
Ðèñ. 53
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
163162
Èç ñêàçàííîãî âûøå ñëåäóåò, ÷òî çàïèñè
xy arcsin=
è
yx sin=
,
,2/2/ p££p- y
ýêâèâàëåíò-
íû. Ïîäñòàâèâ â ðàâåíñòâî
yx sin=
âìåñòî ó åãî âû-
ðàæåíèå, ò. å.
,arcsin x
ïîëó÷èì
)(arcsinsin xx =
.
Ñëåäîâàòåëüíî, äëÿ ëþáîãî õ èç [1, 1] èìååì
.2/arcsin2/,)(arcsinsin p££p-= xxx
127. Ôóíêöèÿ y = arccos x. Ôóíêöèÿ
xy
cos
=
óáûâàåò íà îòðåçêå [0, p], ïðèíèìàåò íà íåì âñå çíà-
÷åíèÿ îò 1 äî 1 (ñì. ðèñ. 49). Çíà÷èò, äëÿ ôóíêöèè
xy
cos
=
, ðàññìàòðèâàåìîé íà îòðåçêå [0, p], ñóùåñòâó-
åò îáðàòíàÿ ôóíêöèÿ. Îíà îáîçíà÷àåòñÿ
xy
arccos
=
(÷èòàåòñÿ: «àðêêîñèíóñ õ»).
Ãðàôèê ôóíêöèè
xy
arccos
=
ïîëó÷àåòñÿ èç ãðà-
ôèêà ôóíêöèè
xy
cos
=
,
,0 p££ x
ñ ïîìîùüþ ïðå-
îáðàçîâàíèÿ ñèììåòðèè îòíîñèòåëüíî ïðÿìîé ó = õ
(ðèñ. 53).
Ïåðå÷èñëèì ñâîéñòâà ôóíêöèè
:arccos
xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ îòðåçîê [1, 1].
2
0
. Ìíîæåñòâî çíà÷åíèé îòðåçîê [0, p].
3
0
. Ôóíêöèÿ íå ÿâëÿåòñÿ íè ÷åòíîé, íè íå÷åòíîé.
4
0
. Ôóíêöèÿ óáûâàþùàÿ.
Èç ñêàçàííîãî âûøå ñëåäóåò, ÷òî çàïèñè
=y
xarccos=
è
,0,cos p££= yyx
ýêâèâàëåíòíû. Ïîä-
ñòàâèâ â ðàâåíñòâî
yx
cos
=
âìåñòî ó âûðàæåíèå
,arccos
x
ïîëó÷èì
xx =)(arccoscos
. Ñëåäîâàòåëüíî,
äëÿ ëþáîãî õ èç ïðîìåæóòêà [1, 1] èìååì
.arccos0,)(arccoscos p££= xxx
âñå çíà÷åíèÿ îò 1 äî 1 (ñì. ðèñ. 48). Çíà÷èò, äëÿ
ôóíêöèè
xy sin=
,
,2/2/ p££p- x
ñóùåñòâóåò îá-
ðàòíàÿ ôóíêöèÿ (ñì. ï. 115). Ýòó ôóíêöèþ îáîçíà-
÷àþò
xy arcsin=
(÷èòàåòñÿ: «àðêñèíóñ õ»).
Ãðàôèê ôóíêöèè
xy arcsin=
ìîæíî ïîëó÷èòü èç
ãðàôèêà ôóíêöèè
xy sin=
,
,2/2/ p££p- x
ñ ïîìî-
ùüþ ïðåîáðàçîâàíèÿ ñèììåòðèè ïîñëåäíåãî îòíîñè-
òåëüíî ïðÿìîé ó = õ (ðèñ. 52).
Ïåðå÷èñëèì ñâîéñòâà ôóíêöèè
xy arcsin=
:
1
0
. Îáëàñòü îïðåäåëåíèÿ îòðåçîê [1, 1].
2
0
. Ìíîæåñòâî çíà÷åíèé îòðåçîê
].2/,2/[ pp-
3
0
. Ôóíêöèÿ íå÷åòíàÿ:
.arcsin)(arcsin xx -=-
4
0
. Ôóíêöèÿ âîçðàñòàþùàÿ.
Ðèñ. 52
Ðèñ. 53
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
165164
Èç ñêàçàííîãî âûøå ñëåäóåò, ÷òî çàïèñè
=y
xarctg=
è
,2/2/,tg p<<p-= xyx
ýêâèâàëåíòíû.
Äëÿ ëþáîãî õ èìååì
.2/arctg2/,)(arctgtg p<<p-= xxx
Ôóíêöèÿ
xy ctg=
óáûâàåò íà èíòåðâàëå (0, p),
ïðèíèìàåò íà íåì âñå çíà÷åíèÿ (ñì. ðèñ. 51). Ñëåäî-
âàòåëüíî, íà ýòîì èíòåðâàëå äëÿ ôóíêöèè
xy ctg=
ñóùåñòâóåò îáðàòíàÿ ôóíêöèÿ. Îíà îáîçíà÷àåòñÿ
xy arcctg=
(÷èòàåòñÿ: «àðêêîòàíãåíñ õ»).
Ãðàôèê ôóíêöèè
xy arcctg=
ïîëó÷àåòñÿ èç ãðà-
ôèêà ôóíêöèè
xy ctg=
,
,0 p<< x
ñ ïîìîùüþ ïðå-
îáðàçîâàíèÿ ñèììåòðèè îòíîñèòåëüíî ïðÿìîé ó = õ
(ðèñ. 55).
Ïåðå÷èñëèì ñâîéñòâà ôóíêöèè
:arcctg xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ ìíîæåñòâî R.
2
0
. Ìíîæåñòâî çíà÷åíèé èíòåðâàë (0, p).
3
0
. Ôóíêöèÿ íå ÿâëÿåòñÿ íè ÷åòíîé, íè íå÷åòíîé.
4
0
. Ôóíêöèÿ óáûâàþùàÿ.
5
0
. Ïðÿìûå y = 0 è y = p ãîðèçîíòàëüíûå àñèì-
ïòîòû ñîîòâåòñòâåííî ïðè õ º +× è õ º ×.
Èç ñêàçàííîãî âûøå ñëåäóåò, ÷òî çàïèñè
=y
xarcctg=
è
yx ctg=
,
,0 p<< x
ýêâèâàëåíòíû. Äëÿ
ëþáîãî õ èìååì
.arcctg0,)(arcctgctg p<<= xxx
Ôóíêöèè ó = arcsin x, y = arccos x, y = arctg x
è y = arcctg x íàçûâàþòñÿ îáðàòíûìè òðèãîíî-
ìåòðè÷åñêèìè ôóêíöèÿìè.
129. Àðêñèíóñ, àðêêîñèíóñ, àðêòàíãåíñ è àðêêî-
òàíãåíñ. Îïðåäåëåíèÿ è ñâîéñòâà îáðàòíûõ òðèãîíî-
ìåòðè÷åñêèõ ôóíêöèé (ñì. ïï. 126128) ïîçâîëÿþò
èñòîëêîâàòü èõ ñëåäóþùèì îáðàçîì:
128. Ôóíêöèè y = arctg x, y = arcctg x. Ôóíê-
öèÿ
xy tg=
âîçðàñòàåò íà èíòåðâàëå
),2/,2/( pp-
ïðèíèìàåò íà íåì âñå çíà÷åíèÿ (ñì. ðèñ. 50). Ïîýòî-
ìó íà óêàçàííîì èíòåðâàëå äëÿ ôóíêöèè
xy tg=
ñóùåñòâóåò îáðàòíàÿ ôóíêöèÿ. Îíà îáîçíà÷àåòñÿ
xy arctg=
(÷èòàåòñÿ: «àðêòàíãåíñ õ»).
Ãðàôèê ôóíêöèè
xy arctg=
ïîëó÷àåòñÿ èç ãðà-
ôèêà ôóíêöèè
,2/2/,tg p<<p-= xxy
ñ ïîìîùüþ
ïðåîáðàçîâàíèÿ ñèììåòðèè îòíîñèòåëüíî ïðÿìîé ó =
= õ (ðèñ. 54).
Ïåðå÷èñëèì ñâîéñòâà ôóíêöèè
:arctg xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ ìíîæåñòâî R.
2
0
. Ìíîæåñòâî çíà÷åíèé èíòåðâàë
).2/,2/( pp-
3
0
. Ôóíêöèÿ íå÷åòíàÿ:
.arctg)(arctg xx =
4
0
. Ôóíêöèÿ âîçðàñòàþùàÿ.
5
0
. Ïðÿìûå y = p/2 è y = p/2 ãîðèçîíòàëüíûå
àñèìïòîòû ñîîòâåòñòâåííî ïðè õ º +× è õ º ×.
Ðèñ. 55
Ðèñ. 54
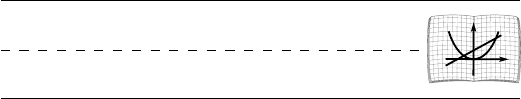
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
165164
Èç ñêàçàííîãî âûøå ñëåäóåò, ÷òî çàïèñè
=y
xarctg=
è
,2/2/,tg p<<p-= xyx
ýêâèâàëåíòíû.
Äëÿ ëþáîãî õ èìååì
.2/arctg2/,)(arctgtg p<<p-= xxx
Ôóíêöèÿ
xy ctg=
óáûâàåò íà èíòåðâàëå (0, p),
ïðèíèìàåò íà íåì âñå çíà÷åíèÿ (ñì. ðèñ. 51). Ñëåäî-
âàòåëüíî, íà ýòîì èíòåðâàëå äëÿ ôóíêöèè
xy ctg=
ñóùåñòâóåò îáðàòíàÿ ôóíêöèÿ. Îíà îáîçíà÷àåòñÿ
xy arcctg=
(÷èòàåòñÿ: «àðêêîòàíãåíñ õ»).
Ãðàôèê ôóíêöèè
xy arcctg=
ïîëó÷àåòñÿ èç ãðà-
ôèêà ôóíêöèè
xy ctg=
,
,0 p<< x
ñ ïîìîùüþ ïðå-
îáðàçîâàíèÿ ñèììåòðèè îòíîñèòåëüíî ïðÿìîé ó = õ
(ðèñ. 55).
Ïåðå÷èñëèì ñâîéñòâà ôóíêöèè
:arcctg xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ ìíîæåñòâî R.
2
0
. Ìíîæåñòâî çíà÷åíèé èíòåðâàë (0, p).
3
0
. Ôóíêöèÿ íå ÿâëÿåòñÿ íè ÷åòíîé, íè íå÷åòíîé.
4
0
. Ôóíêöèÿ óáûâàþùàÿ.
5
0
. Ïðÿìûå y = 0 è y = p ãîðèçîíòàëüíûå àñèì-
ïòîòû ñîîòâåòñòâåííî ïðè õ º +× è õ º ×.
Èç ñêàçàííîãî âûøå ñëåäóåò, ÷òî çàïèñè
=y
xarcctg=
è
yx ctg=
,
,0 p<< x
ýêâèâàëåíòíû. Äëÿ
ëþáîãî õ èìååì
.arcctg0,)(arcctgctg p<<= xxx
Ôóíêöèè ó = arcsin x, y = arccos x, y = arctg x
è y = arcctg x íàçûâàþòñÿ îáðàòíûìè òðèãîíî-
ìåòðè÷åñêèìè ôóêíöèÿìè.
129. Àðêñèíóñ, àðêêîñèíóñ, àðêòàíãåíñ è àðêêî-
òàíãåíñ. Îïðåäåëåíèÿ è ñâîéñòâà îáðàòíûõ òðèãîíî-
ìåòðè÷åñêèõ ôóíêöèé (ñì. ïï. 126128) ïîçâîëÿþò
èñòîëêîâàòü èõ ñëåäóþùèì îáðàçîì:
128. Ôóíêöèè y = arctg x, y = arcctg x. Ôóíê-
öèÿ
xy tg=
âîçðàñòàåò íà èíòåðâàëå
),2/,2/( pp-
ïðèíèìàåò íà íåì âñå çíà÷åíèÿ (ñì. ðèñ. 50). Ïîýòî-
ìó íà óêàçàííîì èíòåðâàëå äëÿ ôóíêöèè
xy tg=
ñóùåñòâóåò îáðàòíàÿ ôóíêöèÿ. Îíà îáîçíà÷àåòñÿ
xy arctg=
(÷èòàåòñÿ: «àðêòàíãåíñ õ»).
Ãðàôèê ôóíêöèè
xy arctg=
ïîëó÷àåòñÿ èç ãðà-
ôèêà ôóíêöèè
,2/2/,tg p<<p-= xxy
ñ ïîìîùüþ
ïðåîáðàçîâàíèÿ ñèììåòðèè îòíîñèòåëüíî ïðÿìîé ó =
= õ (ðèñ. 54).
Ïåðå÷èñëèì ñâîéñòâà ôóíêöèè
:arctg xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ ìíîæåñòâî R.
2
0
. Ìíîæåñòâî çíà÷åíèé èíòåðâàë
).2/,2/( pp-
3
0
. Ôóíêöèÿ íå÷åòíàÿ:
.arctg)(arctg xx =
4
0
. Ôóíêöèÿ âîçðàñòàþùàÿ.
5
0
. Ïðÿìûå y = p/2 è y = p/2 ãîðèçîíòàëüíûå
àñèìïòîòû ñîîòâåòñòâåííî ïðè õ º +× è õ º ×.
Ðèñ. 55
Ðèñ. 54
