Martin P.M. Handbook of Deposition Technologies for Films and Coatings, Third Edition: Science, Applications and Technology

Подождите немного. Документ загружается.

Thin Film Nucleation, Growth, and Microstructural Evolution 581

12.4.2 Two-Dimensional Island Coalescence

Continuing with the TiN results discussed above: at higher partial monolayer coverages,

signiﬁcant island coalescence is observed on TiN(001) as well as TiN(111) surfaces.

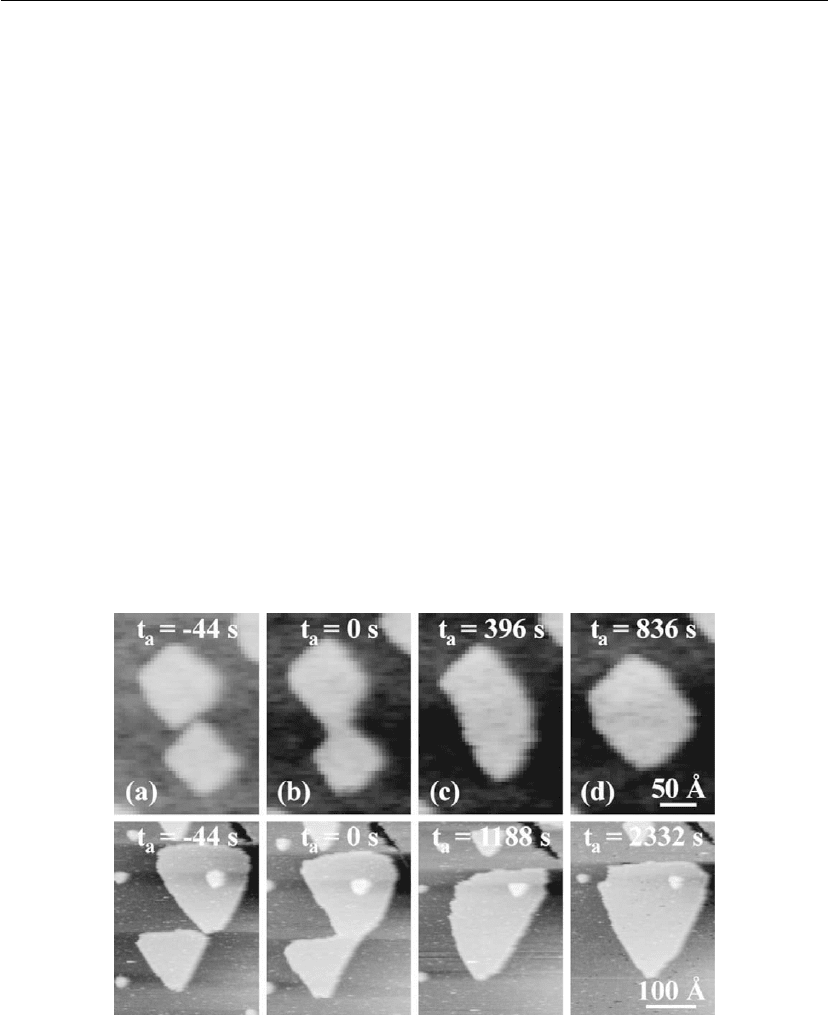
Figure 12.23 shows typical in situ high-temperature STM images, from one of a large number

of video ﬁles (200–400 images per movie acquired at a constant rate of 44 s/frame), of

equilibrium-shaped TiN island coalescence and relaxation on both orientations [69]. In these

experiments, the layers were grown by reactive evaporation in UHV. The upper panels

correspond to TiN(001) island coalescence during annealing under N

overpressure at

= 850

◦

C, while the lower panels correspond to truncated hexagonal TiN(111) islands

at T

= 873

◦

The square TiN(001) islands initiate coalescence at polar <100> corner facets which, from

quantitative island coarsening and shape ﬂuctuation analyses as a function of step orientation,

are known to have high step energies and low stiffnesses [61, 63, 65]. The edge energy

released upon contact results in rapid edge diffusion, driven by the system attempting to

minimize total edge length, leading to the formation of a ﬁgure-eight-shaped island which

relaxes to its equilibrium shape in ∼ 840 s. The TiN(111) islands in the lower panel are

truncated hexagons owing to the anisotropy in alternating <110> 2D island facets in which S

steps form <110>/{100} nanofacets with the TiN(111) substrate while S

steps form

Figure 12.23: (a)–(d): Representative STM images, acquired at 44 s/frame, showing coalescence

and subsequent reshaping of 2D TiN adatom islands during annealing in N

. Upper panel:

TiN(001), T

= 850



C, scan size = 220 × 320

; lower panel: TiN(111), T

= 873



C, scan

size = 290 × 330

. (From [69].)

582 Chapter 12

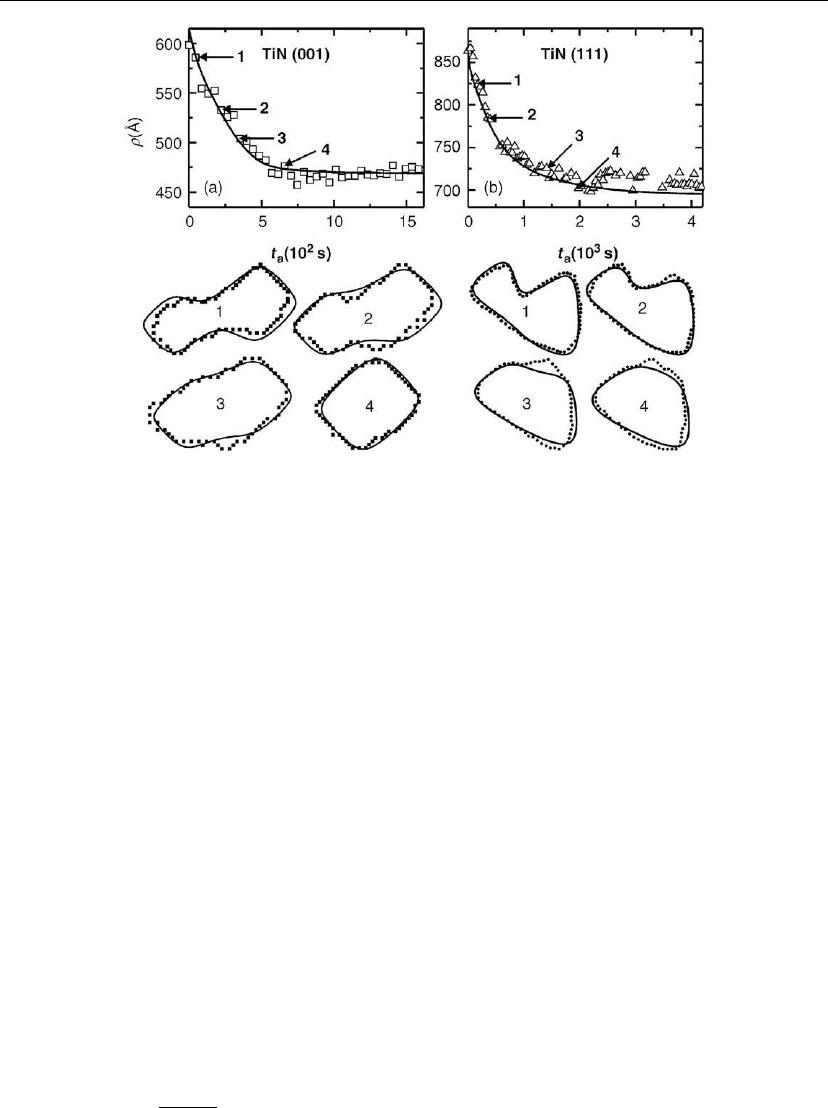
Figure 12.24: Upper panels: island perimeter ρ plotted as a function of annealing time t

for the

(a) TiN(001) and (b) TiN(111) adatom islands shown in Figure 12.23. Lower panels:

time-dependent shapes of the islands labeled 1, 2, 3, and 4 in the upper panels. Symbols are

experimental data while solid lines are calculated curves obtained using Eq. (12.23). (From [69].)

<110>/{110} nanofacets; the ratio of step energy densities (line tensions) is ␤

/␤

= 1.40

[70–72]. The TiN(111) islands initiate coalescence at corner <110> steps resulting in a

sawtooth-shape island which relaxes to its equilibrium shape in ∼ 2330 s.

Experimentally determined values for the total island perimeters ρ(t

) are plotted in

Figure 12.24(a, b) as a function of time (t

= 0 is deﬁned as the time at which the islands make

contact) during relaxation of the TiN(001) and TiN(111) coalesced islands in Figure 12.23.In

both cases, ρ decreases monotonically to a saturated value ρ

corresponding to the

equilibrium island shape. Previous island coarsening and decay measurements showed that

TiN islands on both 001 and 111 surfaces maintain their equilibrium shapes, with thermal

ﬂuctuations, at these temperatures [61, 63, 65, 70–72], indicating that adatom edge mobilities

are higher than surface mobilities and attachment/detachment rates at island edges, as shown

quantitatively below.

In a continuum model for 2D island shape evolution, the normal component v

of the step edge

velocity is related to the step chemical potential μ as [69]

(ϕ, t) =



σ

edge



∇

μ(ϕ, t) (12.23)

Thin Film Nucleation, Growth, and Microstructural Evolution 583

ϕ in Eq. (12.23) is the local step orientation, i.e. the angle of the local step normal,

∇

= (x

+ y

)

−1/2

∂/∂s in which x

and y

represent ﬁrst spatial derivatives of island boundary

coordinates x(s, t) and y(s, t) with respect to arc length element s along the island boundary,

 is the unit TiN molecular area, and σ

edge

is the edge-atom mobility. μ can be expressed in

terms of the step curvature κ(s, t) and the local-orientation-dependent step stiffness

β(ϕ)as

μ(ϕ, t) =

β(ϕ)κ(s, t) (12.24)

Using measured

β(ϕ) values from [63] and [65] (TiN(001)) and [70] and [71] (TiN(111)),

calculated shapes for the islands in Figure 12.23 are shown in the lower panels of Figure 12.24

superimposed on the STM images. Calculated and measured total TiN(001) and TiN(111)

island perimeters ρ, plotted in the upper panels of Figure 12.24, are in good agreement. From

these results, extracted edge mobilities are σ

001

edge

= 22 ± 3.6

A/sat850

◦

C and

111

edge

= 36 ± 7.6

A/sat873

◦

C. The corresponding rates for diffusion- and detachment-limited

island decay on 001 and 111 terraces are σ

001

diff

∼ 4.9×10

−2

A/s and σ

111

det

∼ 7.8×10

−2

A/s,

respectively, at the same temperatures, signiﬁcantly lower than the σ

edge

values. Thus, edge

diffusion is the energetically favored mechanism for mass transport on both TiN(001) and

TiN(111) surfaces under these conditions.

12.5 Stranski–Krastanow Nucleation and Growth

As noted in Section 12.2, the elastic strain energy during heteroepitaxial growth varies as

elas

∝ ε

h, with ε =(a

− a

)/a

. Thus, for a given ﬁlm/substrate system (i.e. a given lattice

parameter misﬁt ε), E

elas

increases linearly with ﬁlm thickness h. It has been known for more

than a half century that highly strained ﬁlms can partially relax via the punch-through of misﬁt

dislocations. Matthews and Blakeslee [73] predicted in the early 1970s, based on

thermodynamic arguments, that the critical ﬁlm thickness h

for obtaining dislocations in

heteroepitaxial systems is:

b(1 − ν

cos

β)n(4h

8πε(1 + ν

)cosλ

(12.25)

where

b is the dislocation Burgers’ vector, ν

is the Poisson ratio of the ﬁlm, β is the angle

between

b and the dislocation line vector, and λ is the angle between the slip direction and the

line in the ﬁlm/substrate interfacial plane which is normal to the line of intersection between

the slip plane and the interface. For growth on 001-oriented diamond and zincblende structure

semiconductors, the primary slip planes are {111} with the dislocation line and Burgers’

vectors along <110> such that β = λ =60

◦

and cosβ = cosλ = 0.5. The agreement between the

predictions of Eq. (12.25) and measurements from well-annealed ﬁlms is quite good; however,

584 Chapter 12

as-deposited layers often have critical thicknesses much higher than the thermodynamic

predictions of the Matthews–Blakeslee model, depending on the growth temperature and

deposition rate, due to kinetic constraints. That is, there is a relatively high activation energy

for nucleating misﬁt dislocations [74].

A competing relaxation mechanism to dislocation formation, multiplication, and glide is

strain-induced roughening or S-K growth. In Section 12.4, it was shown, based on a

consideration of surface energy terms in Eq. (12.9), that 2D growth is energetically favorable

when a

s−v

≥ a

f−v

+ a

s−f

. This is a trivial thermodynamic statement for

homoepitaxy in a clean environment. For heteroepitaxial growth, the equation predicts that

lower surface tension ﬁlms will grow in a 2D mode with smooth surfaces on higher surface

tension substrates, assuming relatively low interfacial energies (e.g. Ge/Si(001),

InSb/GaAs(001), Ag/Mo(001), YBa

7−␦

/SrTiO

(001), etc.). However, such an analysis

neglects another important thermodynamic factor, the elastic energy E

elas

. Including this term,

the equation becomes a

s−v

≥ a

f−v

+ a

s−f

elas

. Thus, for a given normalized

lattice parameter mismatch between the ﬁlm and substrate, even if the difference in surface

tensions favors 2D growth, the strain energy cost begins to dominate above a critical ﬁlm

thickness h

S−K

leading to a transition from initially 2D to 3D growth as originally predicted by

Stranski and Krastanow [16]. That is, the decrease in system strain energy associated with

island dilatational relaxation becomes larger than the energy cost to produce new surface area

(see Figure 12.2).

Strain-induced roughening is favored over dislocation formation by higher ﬁlm/substrate

lattice-parameter mismatch and higher growth temperatures [75, 76]. The requirement for

relatively high T

values to activate strain-induced roughening derives from kinetic

limitations to uphill diffusion (i.e. overcoming the step edge and formation energies) as

discussed in the following sections. Tersoff and LeGoues [74] showed that the activation

energy for strain-induced roughening decreases rapidly with increasing misﬁt strain ε, varying

as ε

−4

. In contrast, the activation energy for dislocation nucleation and multiplication varies

much more slowly with layer strain, yielding an ε

−1

dependence.

12.5.1 S-K Mechanism and Examples

A simple elastic stability analysis illustrates the basic physics, as well as the mechanism, of the

S-K 2D to 3D transition. The results show that a ﬂat surface under stress is unstable with

respect to the development of surface roughening with wavelengths λ greater than a critical

value λ

[18, 19].

Consider the growth of an additional monolayer of material B on one or more pseudomorphic

monolayers of B deposited on substrate material A, where a

> a

. Two limiting cases are

Thin Film Nucleation, Growth, and Microstructural Evolution 585

Figure 12.25: Schematic illustrations of two limiting cases in the deposition of an additional B

layer on a stack of pseudomorphic B layers on substrate A for which a

> a

. Left ﬁgure: the

upper B layer grows pseudomorphically. Right ﬁgure: the upper B layer forms an islanded

square-wave of amplitude 2h and wavelength λ.

illustrated schematically in Figure 12.25. In the ﬁrst case, the ﬁlm continues to grow

coherently at the expense of an increase in the system elastic energy per unit volume E

elas, V

In the second case, the ﬁlm breaks up into islands separated by λ at the expense of increasing

the total surface energy per unit area γ

. To further simplify the problem, the surface

morphology of the rough ‘one-dimensional’ (actually, 1 + 1 D) ﬁlm is a square wave of

peak-to-peak amplitude 2h and it is assumed that the roughening transition completely relaxes

the strain associated with deposition of the upper layer (in reality, strain-induced roughening

generally relaxes only a fraction of the strain).

The difference in total strain energy over one wavelength λ in the two limiting cases is

E =−E

elas,V

hλ + 2

γB

(2h) (12.26)

The elastic energy per unit volume in (1 + 1) dimensions is given by E

elas, V

= Y

/2, in which

is the Young’s modulus of material B. Substituting E

elas, V

into Eq. (12.26) and setting

E = 0 yields a critical roughening wavelength λ

=8γ

. Thus, the system will

spontaneously roughen (island) in the presence of surface morphological perturbations with

wavelengths greater than

> 8γ

(12.27)

As λ becomes larger than λ

, the cost in additional system surface energy, 4γ

h (which is not a

function of λ), to form 3D islands is less than the increase in elastic strain energy, E

elas,V

hλ,

associated with the growth of an additional 2D commensurate layer. Conversely, if λ < λ

, the

increase in surface energy is much larger than the small decrease in elastic strain energy (λ is

too small) and the surface roughening perturbation dissolves.

Note that in three dimensions, the S-K transition is just another stability problem, similar to

the thermodynamic formulation of cluster nucleation in Section 12.2. The energy cost to form

586 Chapter 12

an S-K island is proportional to its surface area (i.e. ∝ r

), while the energy cost to deposit an

additional coherent 2D layer is proportional to its volume (i.e. ∝ r

). Thus, there is a critical

S-K island size r* and a corresponding activation barrier G*. Strain relaxation due to S-K

island formation must overcome the increase in surface energy to allow continued island

growth.

An example of a system exhibiting S-K behavior is the growth of the tetragonal-structure

low-melting point (T

= 156.6

◦

C) metal In on Si(001)2×1 [20, 77]. This material system has a

very large lattice parameter misﬁt, −40% tensile (a

= 3.2523

A with c

= 1.52, and

= 4.5309

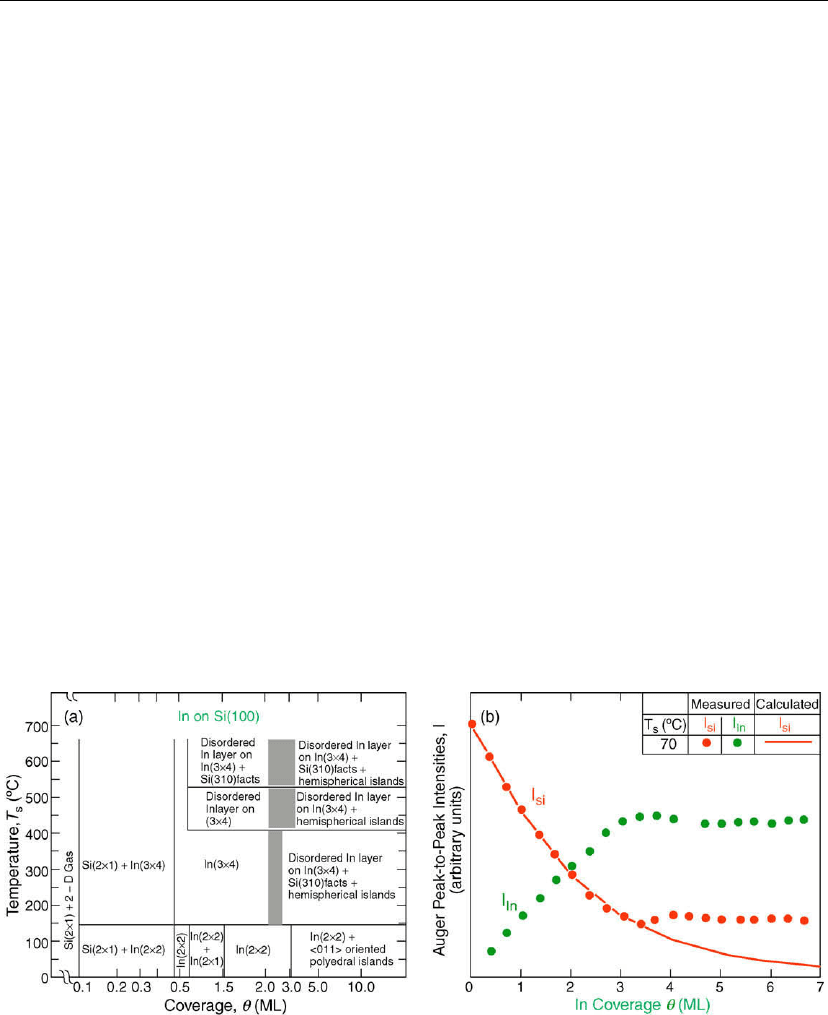
A). The surface phase diagram for In/Si(001)2×1 is shown in Figure 12.26(a). For

< 150

◦

C, In is a 2D gas (i.e. no signiﬁcant adatom–adatom interactions) on Si(001) at

coverages θ

up to 0.1 ML, above which 2D In(2×2) islands nucleate and grow. The (2×2)

phase is complete at θ

= 0.5 ML and further MBE In deposition leads to the layer-by-layer

growth of a psuedomorphic epitaxial In(2×1) phase. At In coverages slightly larger than 3 ML

(some supersaturation is required), 3D faceted polyhedral In islands nucleate and grow along

<011> directions orthogonal to the underlying two-domain (2×1) dimer rows.

The in situ Auger electron spectroscopy (AES) results in Figure 12.26(b) exemplify the

characteristic signature of a 2D to 3D S-K transition. For In deposition at T

=70

◦

C, the

intensity I

of the Si 92 eV LM

2, 3

peak decreases linearly with θ

in successive straight

line segments of length 1 ML, in agreement with theoretical predictions for 2D layer-by-layer

growth, up to θ

∼ 3 ML, above which I

remains approximately constant as In evolves to a

3D island growth mode which attenuates the Si AES signal very slowly with increasing In

Figure 12.26: (a) Surface phase diagram for In on Si(001)2×1; (b) peak-to-peak intensities I of

differentiated Si 92 eV LM

2,3

and In 404 eV MN

4,5

Auger lines as a function of In

coverage θ

on Si(001) at 70



C. A calculated I

curve, assuming 2D In growth, is also shown.

(Adapted from [20].)

Thin Film Nucleation, Growth, and Microstructural Evolution 587

Figure 12.27: Scanning electron micrographs of polyhedral In islands on Si(001)2×1-In. The In

layer was deposited by MBE with J

=1.1× 10

−2

−1

(0.016 ML/s) at T

=70



Ctoa

coverage θ

= 200 ML. The In islands are elongated along [011] and [011] directions and the

black background is the In wetting layer. (Adapted from [20].)

coverages. TPD measurements show that the In desorption energy E

decreases from 2.8 eV in

the 2D gas phase to 2.45 eV, approximately equal to the bulk In heat of vaporization, from 3D

In islands [77]. AES results also reveal that the S-K transition occurs at much lower coverages,

∼ 0.5 ML, at T

= 300

◦

C. A decrease in the transition layer thickness with increasing T

typical of S-K systems.

Figure 12.27 shows scanning electron micrographs of In/Si(001) after deposition of an

equivalent thickness corresponding to 200 ML [20]. The black region is the pseudomorphic,

∼ 3 ML thick, In wetting layer which has the Si substrate in-plane lattice parameter as

demonstrated by a combination of low-energy electron diffraction (LEED) and AES

measurements. The elongated In islands above the wetting layer are of the order 8–10 ␮m long

by 1–1.5 ␮m wide and cover only ∼ 7% of the substrate area. Thus, they are extremely tall,

indicating a very large difference in surface tension between bulk In and the pseudomorphic

588 Chapter 12

Figure 12.28: In situ STM image of a Ge {105}-faceted ‘hut’ pyramid, bounded by <100> edges,

grown by GS-MBE from Ge

on Si(001)2×1atT

= 650



C with R = 0.03 ML/s to a coverage

= 4 ML. (From [22].)

In(2×1) wetting layer. Mapping the orthogonal <011> directions of the 3D In islands provides

the layout of the underlying Si(001)2×1 terraces.

The archetypal system for S-K research, owing to the potential importance of quantum dot

(QD) electronics, is Ge/Si(001). A crude estimate of λ

for Ge on Si can be obtained by

substituting bulk properties into Eq. (12.27) (γ

= 0.085 eV-

, Y

= 0.644 eV-

[103 GPa],

and ε = 0.042). This yields λ

≥ 660

A which, based on atomic force microscopy (AFM) and

STM results, is of the correct order of magnitude [76, 78].

Comprehensive in situ STM investigations of Ge/Si(001) (with a lattice parameter mismatch

of 4.2% compressive, a

= 5.4309

A and a

= 5.6575

A) over more than 10 years have shown

that while the simple model presented above captures much of the physics driving the S-K

transition, the details are far richer and more complex. The wetting layer thickness in this

system, as for In/Si(001), is ∼ 3 ML. Figure 12.28 is an in situ image of a Ge QD grown on

Si(001) at T

= 650

◦

Ctoθ

= 4 ML by gas-source MBE (GS-MBE) using Ge

with

R = 0.03 ML/s. The Ge QD is pyramidal in shape, with <100> edges, faces composed of {105}

facets, and a height-to-width aspect ratio h/d = 0.1. This highly perfect QD image raises some

interesting questions. Why is the pyramid bounded by shallow {105} facets, 11.3

◦

to the (001)

substrate surface? The {105} facets are not low-energy planes in the diamond structure.

Moreover, in the absence of other constraints, maximum strain relaxation would favor much

steeper inclinations to allow more dilation and, hence, increased strain relaxation. Thus, there

must be an opposing reaction to result in such a shallow angle. Another question is: how does

the pyramid grow with a constant shape?

The underlying reason for the shallow {105} facets, and the explanation for why the pyramid

aspect ratio remains constant during growth, was ﬁrst provided by Jesson et al. [79]. The facet

Thin Film Nucleation, Growth, and Microstructural Evolution 589

Figure 12.29: A schematic cross-sectional illustration of the growth of {105} faceted Ge pyramids

on Si(001)2×1. (Adapted from [79].)

angle is limited to 11.3

◦

owing to repulsive step–step interactions arising primarily from

elastic monopole and electronic dipole interactions associated with step edge relaxation (the

1D equivalent of 2D surface relaxation) [80, 81]. The Ge {105} facet plane corresponds to

steps that are 1.4

A high and 7

A wide. Increasing the facet angle reduces the step width and is

therefore energetically unfavorable. Layer growth on {105} facets is illustrated in Figure 12.29

[79]. An atom stochastically deposited on step D, for example, decreases the step width and,

thus, increases the system energy due to step–step repulsion, thereby causing the adatom to

move downward in a cascade process to step A. This then allows the addition of another atom

on step B. Continuing in this fashion results in directed self-organized facet-by-facet pyramid

growth with a constant aspect ratio.

The size distribution of Si

1−x

QDs on Si(001) depends on layer composition x through the

lattice parameter misﬁt strain ε and the deposition conditions (T

, R, and θ

SiGe

). However, the

distribution is far smaller than would be expected purely on the basis of random nucleation and

growth of islands. This is due to the presence of a self-limiting mechanism associated with the

formation of {105} faceted Si

1−x

pyramids which causes the growth rate of larger

pyramids to be less than that of smaller ones and, hence, decreases the pyramid size

distribution. Thus, pyramids nucleated earlier are not necessarily larger than those nucleated

later, as demonstrated in Figure 12.30 showing frames from an STM video ﬁle obtained during

solid-source MBE Ge deposition on Si(001) at 300

◦

C with R = 0.001 ML/s [82]. The same

pyramids in subsequent frames are labeled with the same number. Note that the Ge coverages

listed here correspond to the excess Ge deposited above the nominal 3 ML thick wetting layer.

With increasing size, the pyramid growth rate slows. However, since the Ge ﬂux remains

constant, the ‘excess’ Ge adatoms give rise to higher terrace supersaturations and, hence,

additional pyramid nucleation. The latter effect offsets some of the decrease in size

distribution due to size-dependent self-limited growth.

The change in system free energy G due to pyramid formation on a wetting layer is:

G ∝ C

(γ

− γ

− C

elas

V (12.28)

590 Chapter 12

Figure 12.30: In situ STM images of MBE-grown Ge pyramids as a function of coverage (above

the wetting layer) on Si(001)2×1. Image size = 1000 × 1000

, T

= 300



C, and

R = 0.001 ML/s). (From [82].)

and C

elas

contain geometric factors and elastic constants, respectively; γ

and γ

are the Ge

facet and wetting layer surface energies per unit area; and A

and V are the facet area and

pyramid volume. The ﬁrst term in the above equation is the additional surface energy required

to form a {105} facet, while the second term corresponds to the elastic strain energy

released.

It is extremely rare to observe a partially ﬁlled {105} facet. This suggests that the completion

of a new facet involves kinetically-activated nucleation followed by rapid growth of a critically

sized nucleus. As noted above, the arbitrary inclusion of an adatom on an upper pyramid step

is energetically very costly owing to step–step repulsion. It is much more favorable to grow the

facet from the pyramid base upwards. (In addition, for small pyramids, most Ge adatoms

approach from the surrounding wetting layer rather than directly from the vapor). This is

equivalent to the nucleation and growth of a 2D island (here a {105} facet) as illustrated

below.

Consider a rectangular island of height h on a {105} facet of base length s consisting of n steps

(Figure 12.31). Initially, the energy cost to grow the island increases owing to a stress

concentration at the base of the island. However, for sufﬁciently large facet coverage (i.e.

above a critical nucleus size h*), the elastic energy released by pyramid dilation dominates and