Малыхин В.И. Математика в экономике
Подождите немного. Документ загружается.


Приложение
3
КОНТРОЛЬНАЯ
РАБОТА
№ 3
(к
темам
7—9)
В
работе приведены вариант
№ 1 с
указаниями
(и для
других
вариантов)
и
решениями
и еще
варианты
№
2—5.
Внимание!
Вычисления вести либо
в
обыкновенных
дробях,
либо
с
точностью
до
1-го знака
после
запятой.
1.
ТЕКСТ
ЗАДАНИЯ
ВАРИАНТА
№ 1
Вариант
№ 1
Задание
I. Для
функции
z -
(&У
+
I)
2
:
а)
постройте несколько линий уровня;
б)
найдите частные производные 1-го
и
2-го порядков
в
общем
виде
и в
точке
(I,
1)
(убедитесь
в
равенстве
смешанных
про-
изводных);
в)
найдите градиент
в
общем виде
и в
точке
(/,
^,
г)
найдите дифференциал
в
общем виде
и в
точке
(3,
5
К
д)
найдите
производную
в
точке
(0, 0) по
направлению
вектора
е)
пусть
х
=
2/,
у
«
/
2
- 1;
найдите
г/ в
общем виде
и
при t
=
1-
_—_
Задание
П. Для
функции полезности
и -
ух,х
2
.
а)
постройте несколько кривых безразличия;
вч
.
лшдаП
1V
б)
найдите предельные
полезности
в
общем
«ирнвгода
U,
•
проверьте
положительность предельных
полезностей
и
вы
полнение
1-го закона
Госсена
(убывание
предельных
полез
в)
найдите
эластичность полезности
по
товарам
в
общем
виде
и
г)
HaZxe
точ'к;
спроса
в
общем
виде
и при
доходе
40 и
ценах
(4,
1).
Задание
III.
Пусть
производственная
ФУ™""^*^
Кобба-Дугласа.
Чтобы увеличить выпуск
^«52^^
Р^
тов,
надо
увеличить
фонды
на Ь
процентов
или
таменискянР
на
i
процентов.
В
настоящее
время
один
Р*^£.£££
ф
Р
0
нды
водит
продукции
на
М
руб.,
а
всего
работников
L.
Основные
Ф
322

оцениваются
в
Я
руб. Напишите производственную функцию
и
най-
дите
среднюю
и
предельную
производительность
труда,
среднюю
и
предельную
фондоотдачу, среднюю
фондовооруженность,
эластич-
ность
выпуска
по
труду
и
эластичность выпуска
по
фондам.
Данные:
а
=
3, Ъ =
6,
с = 9, М-
10
б
,
L =
1000,
К =
10
ю
.
Задание
IV.
Найдите экстремум функции
z~x
2
+y
i
+
'2x
+
4yii
установите, максимум
это или
минимум.
Задание
V, Для
двухкритериальной
задачи:
Xj
+
Ьх
2
-»
max;
ях,
+
х
2
-»
max;
я,
+
ах
г
<
8;
8л,
+
Ьх
2
< 24;
*,,
Х
2
>
О
найдите
оптимальное решение
по
первому критерию,
при
уровне
притязаний
по
второму
в 0,7 от его
максимума
на
допустимом мно-
жестве,
Данные:
a~2
t
b
= 3.
2,
УКАЗАНИЯ,
РЕШЕНИЯ
И
ОТВЕТЫ
К
ВАРИАНТУ
№ 1
Задание
I.
Решение:
а) см. п. 2
раздела
7,1;
линия
уровня
с
функ-
ции
ДЛ)
— это
множество
точек
U
t
=
{X:
ДА)
=
с},
Найдем
для
функ-
ции
z -
(х
г
у
+
I)
2
линии уровня
0 и 1.
Имеем
^+1=0,
т.е.
У~-\/х
г
(график этой функции
см. на
рис.
1,
а).
Линия уровня
I
—
это
множество
(х*у
+
I)
2
= 1,
т.е. сумма двух множеств;
V(£y
=
0) и
№(&у
~
—2),
Множество
V—
это
объединение координатных осей
№и
OY\
множество
W—
это
график функции
у —
-2/х
2
(рис
1,
б);
,
б)
находим частные производные:
z'
x
~
2(я^
+
1)2*?
=
4*У
+
4хд
*-*
=
2(^
+
\)х
г
-
2xV
+
2Х
2
;
в
точке
(1,
1) они
равны
8 и 4
соответ-
323

ственно;
далее находим
2-е
частные производные;
z"
n
=
12л
2
/
+
4у,
z
»
=
g^Jy
+ 4х,
z"
=
SxV
+
4х,
z"
~
Ж
(смешанные
производ-
ные
z ,
^действительно
равны);
веточке
(1,
1) 2-е
производные:
z
"
=
|б
2"
=
\2,
z" — 2;
"
в) о
градиенте
см. п. 3
раздела
8.2;
градиент
Vz
«
(Э*/Эх,
Эг/Эу),
т.е.
(4ху(^
+ I),
2х
2
(х
2
у
+
1));
в
точке
(2, 3) он
равен
z =
(312, 104);
г)
дифференциал функции
dz
=
z'dx
+
г-,
^;
подставляя
част-
ные
производные, получаем
d?
=
(4^у
+
l))dx
+
(2х?(х»у
+
I))dfl
в
точке
(3,
5) он
равен
2760d*
+
828dy;
д) о
производной
по
направлению
см. п. 3
раздела
8.2;
имеем
х
=
о
+
/,
у
=
о +
4f,
г',
=
г'
Л
х;
+
^
/,,
подставляя
вычисленные
ранее
частные
производные
z',
z'
и
добавляя производные
х\
- 1,
у,
"4,
получаем
<
-
(4яу(х?у
+
1))
•
1 +
(2я?(^у
+ 0) •
4
=
4х(у
+
2эс)(^
+
1)1
в
точке
(0, 0)
производная
по
указанному направлению равна
нулю,
е) о
дифференцировании
по
параметру
см. п. 3
раздела 8.1; име-
ем
z'
=
z'
х'
+
z'
У
1
',
подставляя
вычисленные ранее частные
произ-
водные
L
z'
и
добавляя
производные
х\
-
2,
/,
==
2/,
получаем
z'
t
=
(4яу$у
-f
1))'
2 +
(Ж(х
2
у
+
1))
*
2^;
при
/*
1
х(1)
-
2,
XD
~
и
>
подставляя
все
это, получаем
z
==
8.
Задание
П.
Решение:
подп.
«а»~«б»
см.
пример
3
раздела
8.2;
в)
эластичность полезности
по
первому товару равна
W«V/
/(«А,)
-
1/2,
по
второму
товару
равна также 1/2,
т.е.
эластичности
постоянны;
г)
см.
пример
2
раздела
9.1.
„
в
„„«
У
™-
<Um:
х; =
Q/W,
х;
-
Q/W.
Для
конкретных
данных
за
дания
получаем:
*,'
=
40/8
-
5,
х
г
-
40/2
- 20.
Задание III.
См.
пример
б
раздела
8.1.
Задание
IV.
Решение. Находим частные производные
и
приравни-
ваем
их
к
нулю:
«;-
2,
+
2 - 0
^
х
--^и
-*
^°^
ти
„
Нашли
стационарную
точку
•(-!,
-^.
Для
тою
Ч1
""
в
'
„
s
2
экстремума
в
ней, находим
2-е
частные
производные,
л и
^
>
ft
Л
*
и"
=
О,
С =
и"
=»
2.
Так
как D = АС - В - 4
^
и
ил
то
точка
(-1,
-2)
ейь
точка
минимума
(см.
п. 2
раздела
9.1).
Задание
V.
Решение. Чтобы узнать
максимум
2-й
целевой
функ-
ции,
решаем задачу линейного программирования:
2х,
+
х
г
->
max;
х,
+
2х
2
<
8;
8х,
+
Зх
2
<
24;
х,,
х
2
> 0.
324
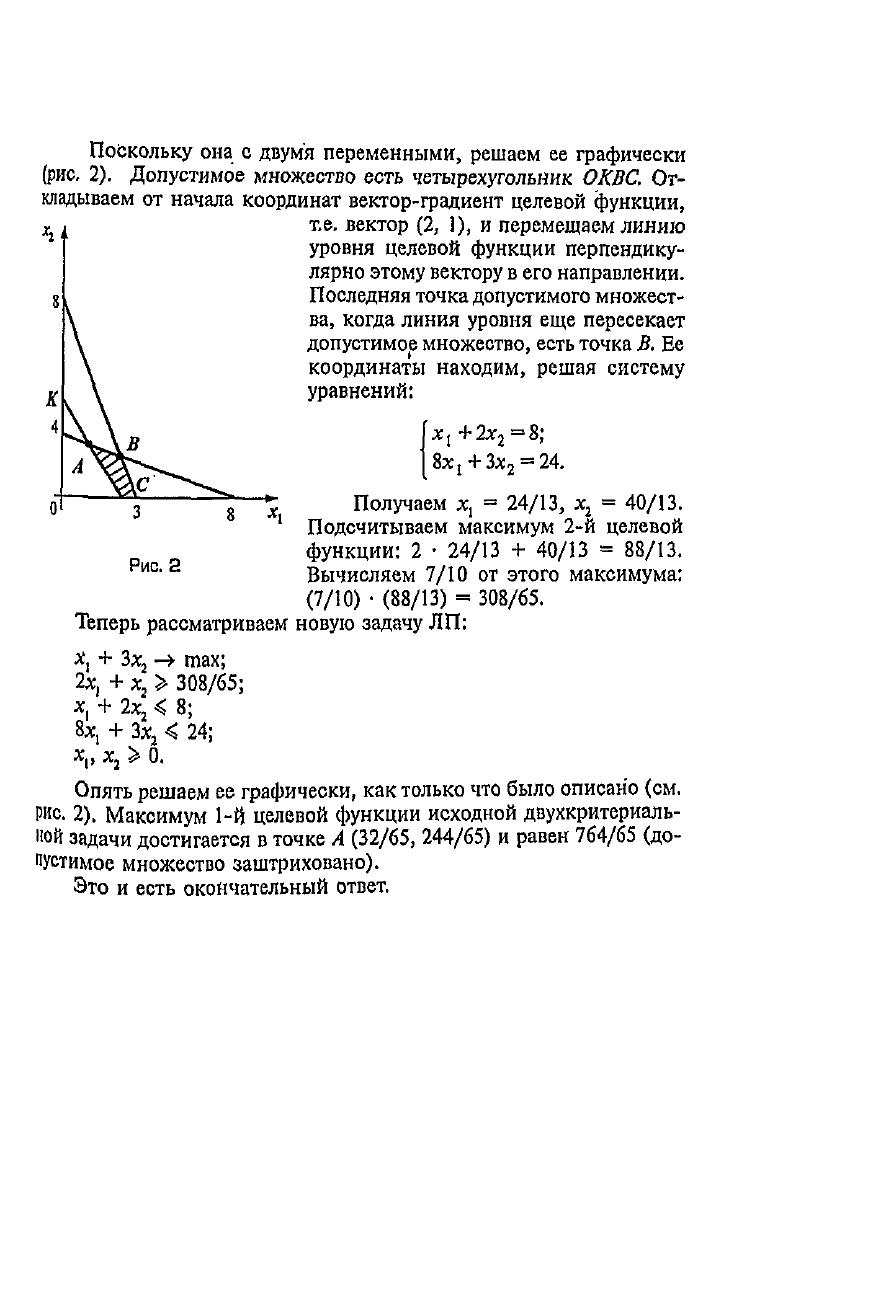
Поскольку
она
с
двумя
переменными, решаем
ее
графически
(рис.
2).
Допустимое
множество
есть
четырехугольник
ОКВС,
От-
кладываем
от
начала координат вектор-градиент целевой функции,
т.е.
вектор
(2,
1), и
перемещаем
линию
уровня
целевой функции перпендику-
лярно этому вектору
в его
направлении.
Последняя точка допустимого множест-
ва,
когда линия уровня
еще
пересекает
допустимор множество, есть точка
В. Бе
координаты находим, решая систему
уравнений:
Х\
т
2Хл
==
oj
8xi
+
3*
2
=
24.
Получаем
х
{
=
24/13,
х
2
=
40/13.
Подсчитываем максимум
2-й
целевой
функции:
2 •
24/13
+
40/13
=
88/13,
Рис-2
Вычисляем 7/10
от
этого максимума:
(7/10)
•
(88/13)
=
308/65.
Теперь
рассматриваем новую задачу
ЛП:
*,
+
Зх
г
-*
max;
2х,
+
х
2
>
308/65;
*,
+
2х
г
<
8;
Ц +
Ъх
г
<
24;
*,,
х
г
>
0.
Опять решаем
ее
графически,
как
только
что
было описано (см.
РИС.
2).
Максимум
1-й
целевой функции исходной
двухкритериаль-
ной
задачи достигается
в
точке
А
(32/65,
244/65)
и
равен
764/65
(до-
пустимое
множество заштриховано).
Это
и
есть окончательный ответ.
1л>
ю
0\
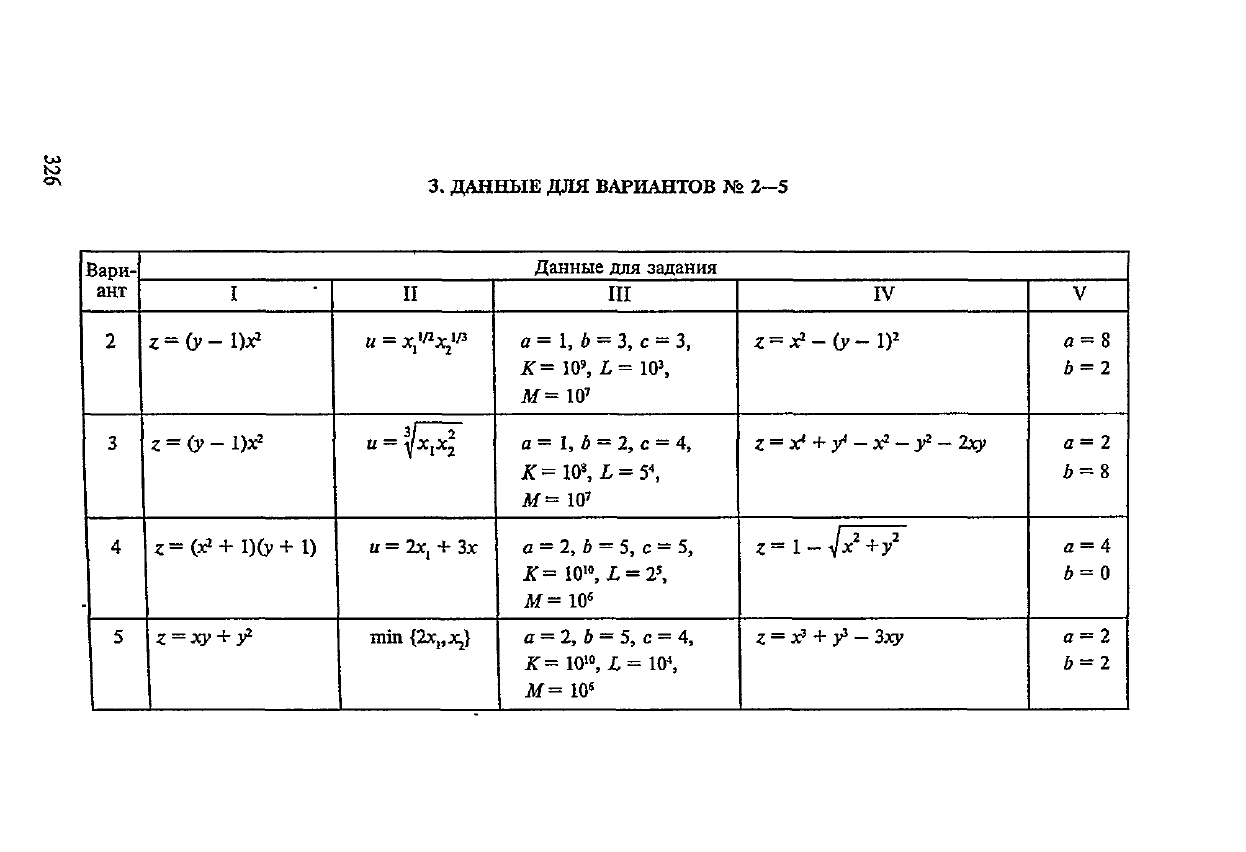
3.
ДАННЫЕ
ДЛЯ
ВАРИАНТОВ
JVi>
2—5
Japii-
ант
2
3
4
5
Данные
для
задания
I
««(у-!)*
г
=
<у-1)э?
z=Cx?+I)(y+l)
г-jp
+
y
1
II
и
=
хфх**
3
з/
Г
ы
—
Y*i*
2
u
=
2x
l
+
3x
min
{2x
!
,jc
1
}
III
а
=
1,
*
=
3, с - 3,
iT=
10
9
,
L=
10
3
,
M=10
7
a
-
1,
b = 2, с - 4,
K=ltf,L
=
S
4
,
M=10
7
a
— 2, 6 = 5, с
=
5,
J5T=
I0
10
,
i
=
2
5
,
M=10
S
u
-
2,
b - 5, с - 4,
ЛГ=
10
10
,
X =
10
4
,
M=
10
6
IV
2
=
^-(y»l)
2
г
-
x
4
+
У
-
л
1
-
j
2
-
2xy
z^l-V^+y
2
г
=
x^
+
3^
—
Зду
V
й
=
8
A
=
2
a
= 2
i
=
8
д
= 4
л
= о
а
= 2
6
= 2

Приложение
4
КОНТРОЛЬНАЯ
РАБОТА
№ 4
(к
темам
1*0—14)
В
работе
приведены вариант
№
I
с
указаниями
(и для
других
вариантов)
и
решениями
и еще
варианты
№
2—5
для
самостоятель-
ного
решения.
Внимание! Вычисления вести либо
в
обыкновенных
дробях,
либо
с
точностью
до
первого знака после запятой.
1.
ТЕКСТ
ЗАДАНИЯ
ВАРИАНТА
№ 1
Вариант
№ 1
Задание
I. А.
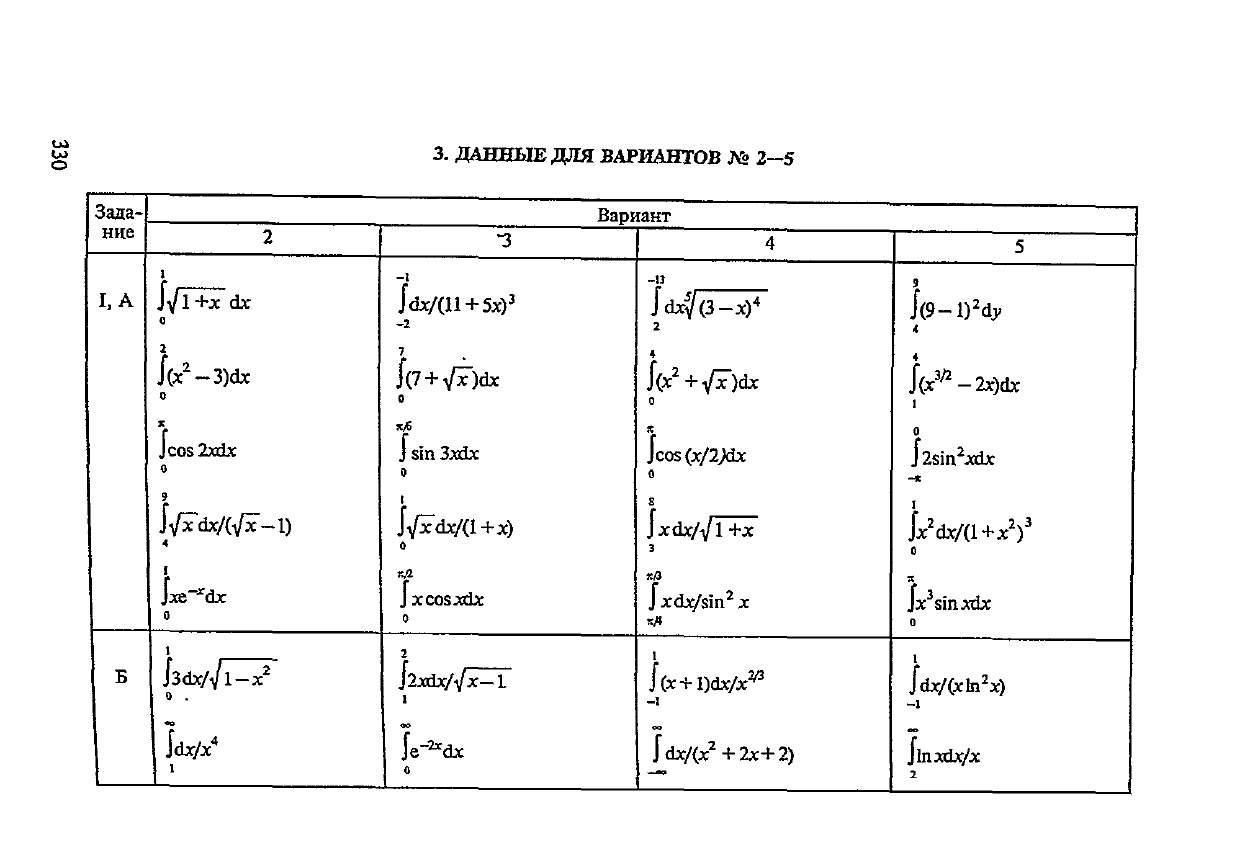
Вычислите определенные интегралы;
2 9
тс/10
тс 1
J(2x~3x
2
)dx,
j2dx/V**,
J
2sin5xdx,
Jjcsinxd*,
J
;cdx/V5-4x.
1
i о
o-i
Б.
Вычислите несобственные интегралы:
1
00
Jlnxdx,
Jdx/(l+*
2
).
0
-TO
В.
Вычислите кратные интегралы. Най-
ти
объем тела-цилиндра
над
плоской облас-
тью
(рис.
1) и
уравнением «крыши»
z-
2х
+
+у.
Найти массу тела-цилиндра
из
предыду-
щей
задачи
с
плотностью
f(M)
^
х + у
4-
2г.
Задание
П. А.
Найдите частное реше-
ние
уравнения,
которое
при
х - 0
принима-
ет
значение
у
=
1:
у'
~
2х +
х\
у'
=
е
41
,
/=
sin
я
cosx
р
иа
-j
Б,
Найдите общее решение уравнения
y'~3x-y
t
y'-y/x-tf.
Задание III.
А.
Установите сходимость
или
расходимость рядов:
оо
со
оо
**>
2
«/(2//
-
1),
I
1/(Я
А/^МГ).
Е (2 +
Н>")/2",
£
I/O'
2
-
4«
+ 5).
«=1
л=Ч
п=1
»=1
327

328
оо
Б.
Найдите радиус сходимости степенного ряда
£
nxf.
л
=
1
2.
УКАЗАНИЯ,
РЕШЕНИЯ
И
ОТВЕТЫ
К
ВАРИАНТУ
№
I
Задание
I.
Решения.
А.
Первые
три
интеграла вычисляются
не-
посредственно, дадим только ответы:
1) -4; 2) 8;
3)"2/5.
Четвертый интеграл вычисляется интегрированием
по
частям.
к
г
*
Имеем:
х
=
и,
sinxdx
=
dv и
потому
jxsmxdx**
(x •
-cosx)|
-
Л
It
-
J(-cos;e)d*
~
-тс • cos
тс
+
Jcosxd*
=
тс
+
smx
\
~
re.
о
о
°
Для
вычисления пятого интеграла используем подстановку
5
- 4х =
£,
после чего получаем
х = (5 -
4я
2
)/4,
ojc
-
~z •
dz/2
и
i i
i
потому
Jxdx//5^¥
=
J(5-?)/4(-^d^(22))=
JU
2
-5)d^8
=
-i
з з
i
=
W24
-
Sz/S)
| =
(1/24
-
5/8)
-
(27/24
-
15/8)
=*
1/6.
з
i
Б.
Несобственные интегралы есть пределы, поэтому
Jlnxdx-
о
i
-
lim
Jlnxdx.
Вычислим
Jlnxcbc
по
частям.
Он
равен
х(1п
х -
О-
е-^О
Е
1
Г
'
Значит,
Jin
xdx
«
х(1п
х - 1)|
=
-1 -
е(1п
е - 1).
Ясно,
что
при
е
~>
О
это
выражение стремится
к -I.
Поэтому исходный
несобственный
интеграл
равен
-1.
Для
второго интеграла дадим только ответ:
тс,
В,
См.
пример
3 из
раздела
П.1,
Ответ:
160/3,

По
поводу
вычисления
массы
тела
см.
пример
4 из
раздела
11.1.
Ответ: 1952/3
=
650,6.
Задание
П.
Решения.
А.
Уравнения решаются непосредственным
интегрированием
с
последующим нахождением произвольной
посто-
янной.
Приведём только ответы:
1) у = х
2
-Ь
хуз
-Ь
1; 2) у
=
е*У4
+
+
3/4;
3) у
=
-cos
2х/4
+
5/4.
Б. Оба
уравнения являются линейными
и
решаются методом
вариации
произвольной постоянной. Рассмотрим только решение
первого
уравнения. Сначала решаем однородное уравнение
у'
+у
= 0.
Его
общее решение
у -
се~*.
Теперь считаем
с
функцией
от
х,
дифференцируем
и
подставляем
в
исходное уравнение. Получаем
с'-
Зхе*,
откуда
с
=
)3х&
х
.
Этот
интеграл находим интегрированием
по
частям,
получаем
с
~
3(х
-
1)е*.
Окончательно,
у
=
3(х
- 1) +
+
с,е-*.
Задание III. Решения.
А. 1)
Поскольку общий член ряда стре-
мится
к
1/2,
а не к
нулю,
то ряд
расходится (см.
п. «В» из
разде-
ла
14.1);
2) см.
пример
3
раздела 14.1;
3)
сходится,
устанавливается
сравнением
с
геометрической убывающей прогрессией
со
знамена-
телем
1/2;
4)
сходится,
так
как
lim
(1/(п
2
~
4«
+
5))/(1/«
а
)
- 1
(
см
-
Те
~
Ч—\.ПЛ
„_>00
орему
2 из п. 3
раздела 14.1).
.
Б.
Используем
замечание
после
теоремы
5 из
раздела
14.1.
Для
исследуемого
ряда
s
n
=
'У/Г->
t;
значит,
радиус сходимости исследу-
емого
ряда равен единице.
329