Малыхин В.И. Математика в экономике
Подождите немного. Документ загружается.


Приложение
1
КОНТРОЛЬНАЯ
РАБОТА
№ 1
(к
темам
1—3)
Внимание!
Вычисления вести либо
в
обыкновенных
дробях,
либо
с
точностью
до
1-го знака
после
запятой.
1.
ТЕКСТ
ЗАДАНИЯ
И
ДАННЫЕ
ДЛЯ
ОДНОГО
ВАРИАНТА
Задание
I. В
пространстве трех товаров рассмотрите
бюджетное
множество
при
векторе
цен Р и
доходе
Q.
Опишите
его и его
границу
с
помощью обычных
и
векторных неравенств
и
равенств,
изобразите
бюджетное множество
и его
границу графически.
В
ответе дайте
чис-
ло —
объем
бюджетного
множества.
Данные:
Р = (2, 5, 6),
£>
=
30.
Задание
П.
Рассмотрите задачу оптимального
планирования
с
матрицей норм расхода
А,
векторами удельных прибылей
С и
запа-
сов
ресурсов
В,
Данные:
А
=
(*
\
],
С=
(2, 2),
5=
({?).
1.
Решите
эту
задачу графическим
методом,
найдите
оптималь-
ный
план, максимальную прибыль, остатки ресурсов.
Какие
ресурсы
являются
«узкими местами» производства?
2.
Составьте двойственную задачу
и
решите
ее,
используя
-но
теорему двойственности
и
зная
ответ
к
исходной задаче
из п.
I.
3.
Найдите следующие произведения векторов
и
матриц
(не
ищите
в
произведениях экономического смысла!) (символ
обозна-
чает
операцию транспонирования):
СА,
АВ,
СВ,
ВС,
АС
Г
,
В А, В >
СГ'Ж
Задание
III.
Даны
зависимости спроса
D и
предложения
S
от
цены^.
Найдите равновесную
цену,
выручку
при
равновесной
цен
•
Найдите
цену,
при
которой выручка максимальна,
и
саму
эту
мак^
мальную
выручку.
Данные:
D
=
400 -
Sp,
S
«
100
+
5р.
Задание
IV
(Модель
Леонтьева). Даны вектор
С
непроизвод-
ственного
потребления
и
матрица
А
межотраслевого
баланса,
ш
дите вектор валового
выпуска,
обеспечивающий
данный
вектор
треблсния,
312

Задание
V
(Модель Неймана). Даны матрицы
А,
Б
технологиче-
ских
процессов,
вектор
цен
Рп
вектор
S
начальных запасов. Найдите
интенсивности
г
р
^
технологических
процессов,
максимизирующие
стоимость выпуска продукции
за
один производственный
цикл,
и
эту
саму максимальную стоимость.
.
Данные:
А
=
(|
*,
),
J,.(*
£
),
Р
=
0
,
5))
j=
(").
i
2.
РЕШЕНИЕ
ЗАДАЧ
КОНТРОЛЬНОЙ РАБОТЫ
Задание
I,
Вектор
цен Р -
(/>,,
р
у
р
3
),
набор товаров
Х- Ц,
х
2
,
^),
Бюджетное
множество
5
— это
множество
всех
наборов
товаров
J,
которые
потребитель может купить
на данное
количество денег
Q
при
данных ценах
Р
(при этом
не
обязательно тратить
все
деньги).
Бюджетное множество можно описать
так
(набор товаров
— это
век-
тор-столбец,
но по
типографским соображениям записываем
его в
виде
вектора-строки);
а)
обычными неравенствами
р,*,
+
р
г
х
г
+
ад
<
Q,
Хр
*
2
,
х
3
>
0;
б)
векторными
неравенствами
Р •
X
<
Q,
Х>0.
Граница
бюджетного множества
— это его
часть,
это
множество
наборов
товаров,
которые стбят
в
точности
Q.
Граница
бюджетного
множества
описывается
так:
а)
обычными
равенствами
/>,«,
+
PJX,
+
р&
«
б,
х,,
Хр
X)
>
0;
б)
векторными
равенствами
/>•*«&
^Г>0.
Для
случая
трех
товаров
бюджетное
множество
представляет
собой
трехгранную пирамиду, одна вершина которой есть начало
ко-
ординат,
а три
другие
—
точки
(?//>„
Q/p
v
Q/p^
на
осях
ОХ
{
>
OX
V
ОХ
У
Граница
же
бюджетного множества
— это
основание этой
пирамиды,
если
ее
вершину считать началом
координат.
Объем бюджетного
множества
равен
(l/3}(Q/
Pl
)(\/2)(Q/p
2
)(Q/p^
При
наших данных
объем
равен
V- 75,
313
314
Задание
II.
1.
Решение этой задачи графическим методом
см. в
п.
З
г
раздел 3.1.
2.
Двойственную задачу составляем
по
правилам
из п. 2,
раз-
дел
3.2:
S(x
lt
х
2
)
=
2x
l
+
2х
2
-»
max,
N(y
lt
у
2
)
=
6у
}
+
6у
г
-»
min,
3x
l
+
х
2
<
б, |
у
{
>
0
Зу,
+
у
2
>
2,
х,
+
2х
2
<
б,
17
2
>
0
j»,
+
2^
2
>
2,
х,,
х
2
>
0,
y
lt
у
2
>
0.
Решение
двойственной
задачи
с
использованием
2-Й
теоремы
двойственности
и
ответа
к
исходной задаче
см. в п. 3,
раздел 3.2,
Приведем
только ответы:
у
}
~
2/5,
у
2
~
4/5,
#
min
=
36/5.
3.
Приведем только ответы:
04=
(8, 6),
АВ=
(jg
),
СВ°*
(24),
ВС=
(}^
Ц
},
&А**
(24,18),
(
я
\
/
ю
I
1
?
^
0
г^дт
_
1Z
1Z
б
j,
с
в
-^
12
12
j.
Задание
Ш.
Точка равновесия
характеризуется
равенством спро-
са и
предложения:
D(p)
—
б'Ср),
т.е.
400 -
5р
=
100 +
5р
-4
р
=
30.
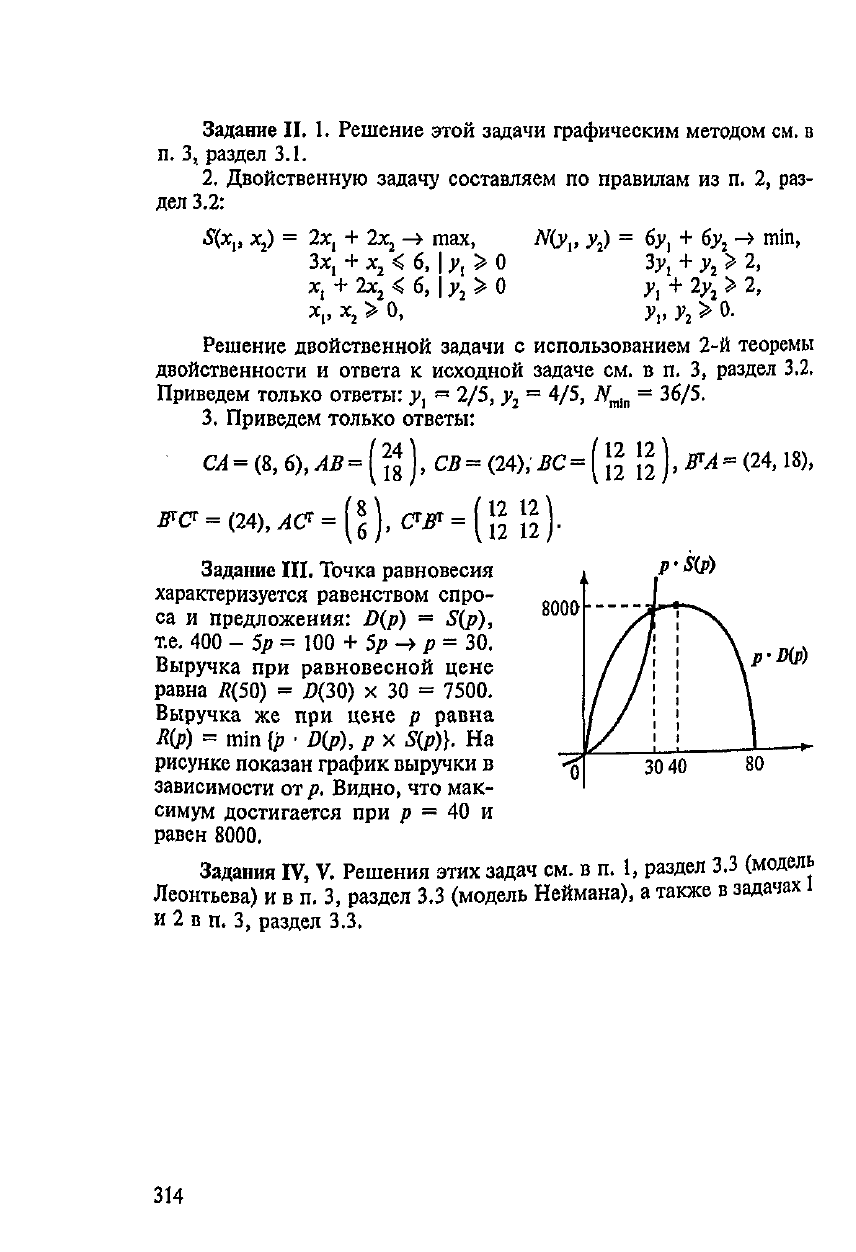
Выручка
при
равновесной цене
равна
Л(50)
=
ДЗО)
х 30
=
7500.
Выручка
же при
цене
р
равна
Л(р)
=
min
{р
•
D(p),
р х
S(p)}.
На
рисунке
показан график выручки
в
зависимости
от
р.
Видно,
что
мак-
симум
достигается
при р — 40 и
равен
8000.
Задания
IV, V.
Решения этих задач
см. в п. 1,
раздел
3.3
(модель
Леонтьева)
и в п. 3,
раздел
3.3
(модель
Неймана),
а
также
в
задачах
i
и
2 в п. 3,
раздел 3.3.
3.
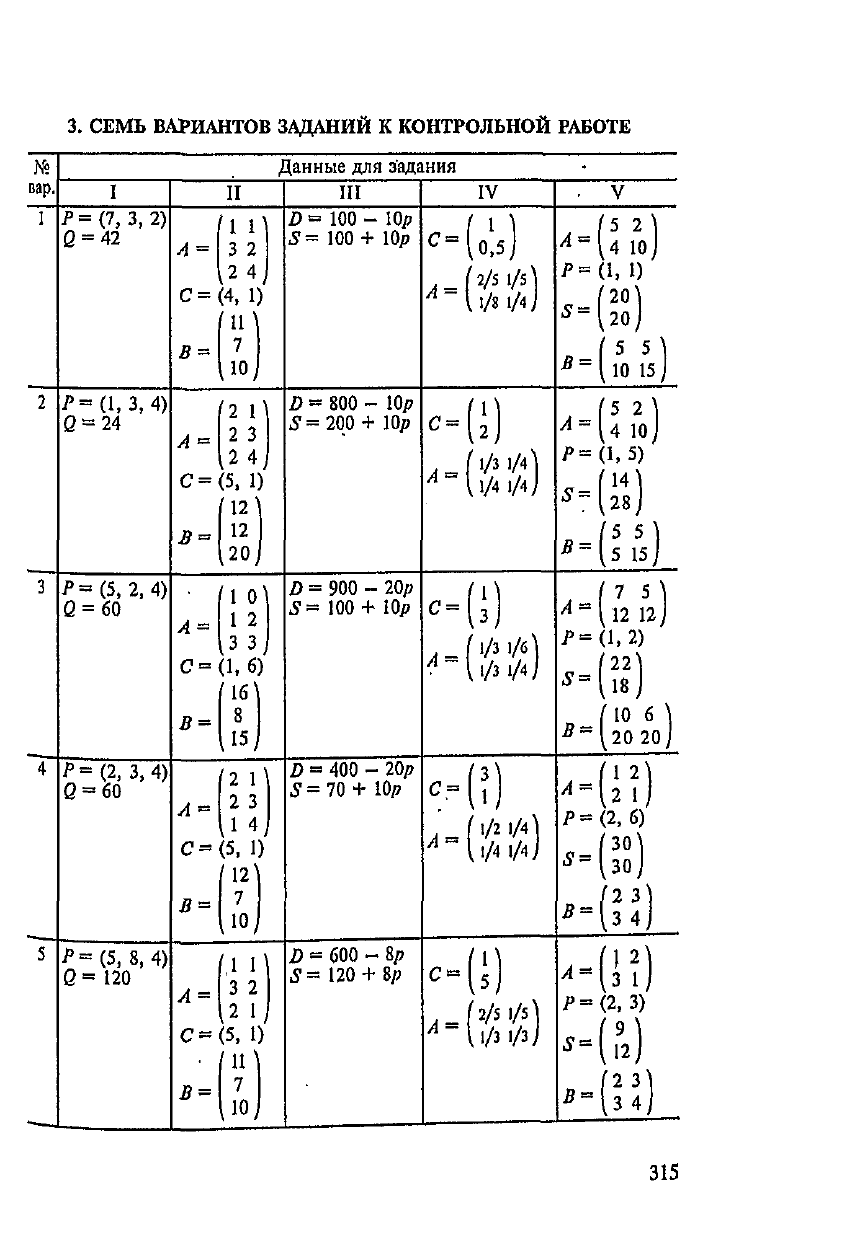
СЕМЬ ВАРИАНТОВ ЗАДАНИЙ
К
КОНТРОЛЬНОЙ РАБОТЕ
№
вар.
1
2
3
4
5
Данные
для
з'адания
I
?
=(7,3,2)
G
=
42
/»=<!,
3,4)
Q«24
Р-С5.2.4)
(3
=
60
Я
=(2,
3,4)
G
=
60
^=(5,8,4)
G=
120
II
А
=
С
=
В-
А~
С
=
в~
А
<--'
i
Л
"""
С
=
Е>
—
Л
—
Л
—
Л —
1
1
i
1
3 2
2 4
(4,1)
11
\
7
10
j
^2
1
£*
i
2
3
124
(5, 1)
'12
1
12
I
20
,
fl
0
1
V/
1
2
1*3
(1,6)
16
\
8
15
j
2 1
2
3
1
4
\
/
\
/
\
/
С
-(5,
1)
71
ь_л
jS
**
Х
^
=
с«
£
=
12'
7
10
f,l
I
3 2
i
2
I
(5,
1)
a
1
7
10
III
D
=
100
-
IQp
^=100+
Юр
D
«
800
-
10/7
J
=
200 +
\Qp
D
= 900 -
20/>
5
и 100 +
IQp
D
»
400
-
20/>
5
= 70 +
10/7
Д
=
600 -
8/7
5
~
120 +
8p
IV
f
1
}
C
=(o,5J
^-f
2
/
51
/
5
)
''-bMAJ
n\
C
=(2J
,
f
1/31/41
A
-(^>/<>
fO
с=
(з)
^•(SS)
".-(?)
,_f
1/21/41
^"li/iiAJ
«-(i)
,_f0i/s)
^"
I
1/3
1/3j
•
V
/5 2
\
Л
—
1
"V
4
10
J
p«(l,l)
5
-f
20
]
*~
\2QJ
0
I
5
5
\
B
-\IQ
is
J
f5
2
^
A
—
л
^4
10J
/»-(!,
5)
S-(
14
л
^28j
Д-f
5
M
*-(5lS)
(75}
A
~\12
12
j
P=(U2)
(22}
,V
=
.n
л
UH
(
10
б
^
5
"^2020/
fl*\
Am
(*i}
P
=(2,
6)
(
А
Я
\
30
30
)
(23}
д
=
I
-
.
B
\34j
-и?)
?=(2.3)
(
n
\
n]
(2
3}
'-134J
315
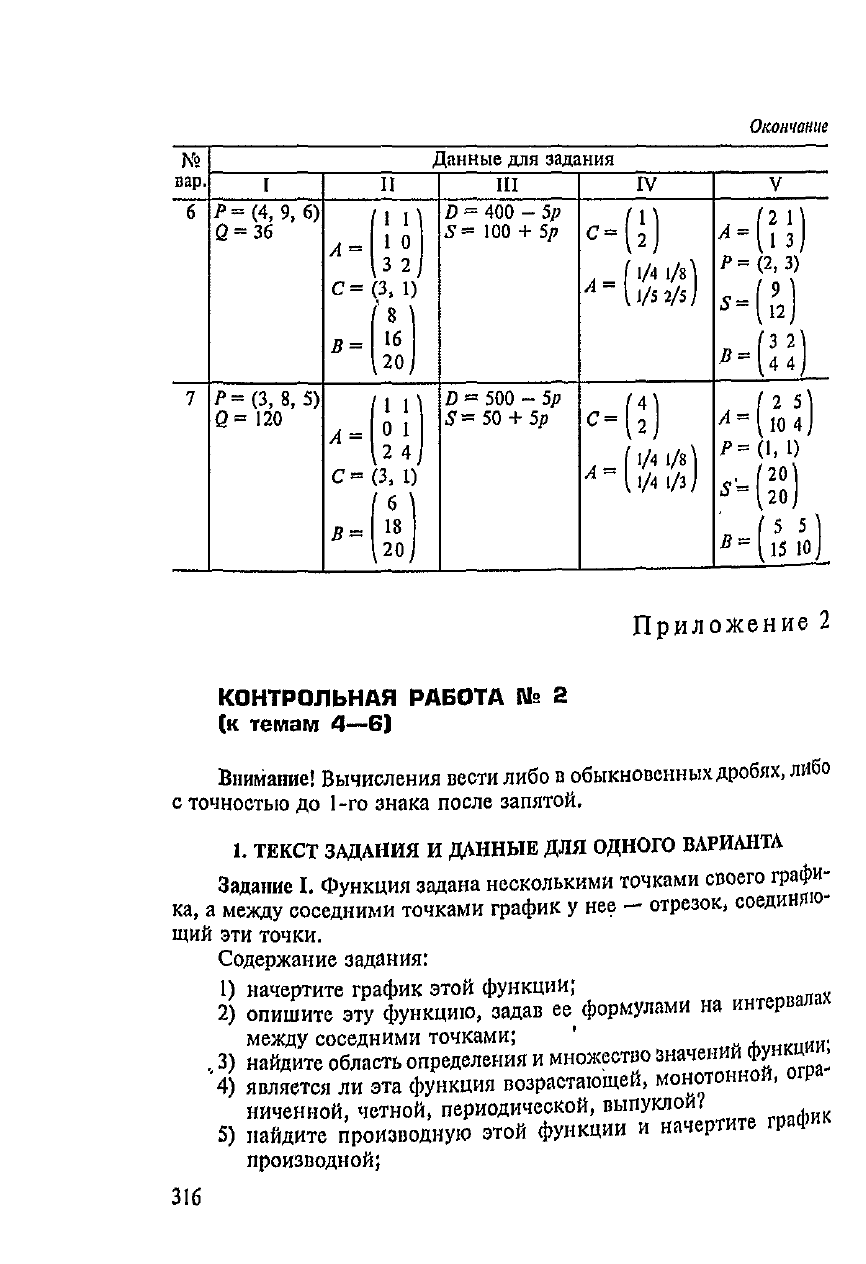
Окончание
№
Данные
для
задания
вар.
i
П
III IV V
б
?
=
(4,9,б)
i
i
Z>
=
400-5/7
fi\
(
2
\\
а
=
3б
j'
5=100
+
5/>
C-(
2
J
^
=
(
13
J
32
л
('/«А!
'"Р'?
С=СЗ,1)
H0
2
/J
Je
(9)
5=
16
/32)
М
M44J
7
*
«(3,8,5)
!
м
Л-500-5р
/
4
\
/
2
5)
Q=120
*|
.У=50
+
5р
C=(
2
j
^
=
[l04j
24
/
,
(*Ф\
?
"
/
°'\
)
C.(3.«
-(
I/41/3
J
,
и
(2в)
Д«
18
»
f
5
5
1
5
[20]
5!=
ll5!oJ
Приложение
2
КОНТРОЛЬНАЯ
РАБОТА
№
2
(к
темам
4—6)
Внимание!
Вычисления вести либо
в
обыкновенных
дробях,
либо
с
точностью
до
1-го знака после запятой.
1.
ТЕКСТ
ЗАДАНИЯ
И
ДАННЫЕ
ДЛЯ
ОДНОГО
ВАРИАНТА
Задание
I.
Функция задана несколькими точками своего
графи-
ка,
а
между соседними точками график
у нее
-
отрезок,
соединяю-
щий
эти
точки.
Содержание задания:
1)
начертите
график этой функции;
„„„тх
2)
опишите
эту
функцию, задав
ее
формулами
на
интервалах
между соседними точками;
'
^.„^„ни'
. 3)
найдите область
определения
и
множество
значений
№*«"£
4)
является
ли эта
функция
возрастающей,
монотонной,
огра
ничейной,
четной,
периодической,
выпуклой/
5)
найдите
производную
этой функции
и
начертите
график
производной;
316

6)
найдите
критические точки,
экстремумы,
нули,
наибольшее
и
наименьшее значения функции,
Данные:
(О, 0),
(2,
2),
(5,
-1),
(7, 1),
Задание
II.
Дана парабола
у
=
х
2
- х
Подберите новую параболу
с
ветвями
вниз справа
от
данной, чтобы данная парабола
в
точке
с
абсциссой
d
>
I
плавно
(т.е.
без
разрыва производной) переходила
в
новую.
Части Двух парабол образуют новую функцию. Найдите про-
изводную
этой новой функции
и
нарисуйте
ее
график. Найдите вто-
рую
производную этой функции
и
также нарисуйте
ее
график,
Данные:
d — 2.
Задание
III. Пусть производственная функция фирмы есть
У
*
Дх)
(объем
основных фондов
х и
выпуск продукции
у
даны
в
стоимостном
выражении). Сейчас объем основных фондов равен
Ъ.
Найдите
среднюю
и
предельную
фондоотдачу,
эластичность выпуска
по
фондам. Решите задачу фирмы
и
найдите оптимальный размер
фирмы,
функцию спроса
на
ресурсы
и
функцию предложения про-
дукции
(в
рассматриваемый момент цену продукции считать
в два
раза
больше
цены
ресурса).
1
"
Данные:
Д*)
«
50
У*
,
Ъ
=
64.
Задание
IV. На
склад
цемент
привозят
в
барже
по
Q
т.
Наклад-
ные
расходы равны
JK.
Издержки хранения
оцениваются
в А
центов
с
тонны
за
сутки. Каждые сутки склад отпускает
Ы
т
цемента.
Нари-
суйте
график изменения
во
времени величины
запаса
на
складе.
Найдите
средние
за
единицу времени
накладные
расходы,
издержки
хранения
и
суммарные издержки. Судя
по
первым двум
издержкам,
оптимален
ли
размер
партии
поставки?
Найдите
по
формуле
Уилсо-
на
оптимальный размер партии поставки.
Данные:
Q
=
2000,
К=
3000,
А
«
20,
М=
100,
Задание
V,
Придерживаясь плана исследования
функции,
по-
стройте
графики следующих функций;
у
-
/(л),
z
M
^(*).
Данные:
f(x)
«
-х
2
+
9х
- 8;
F(x)
=
6х/(\
-
*
2
).
2.
РЕШЕНИЕ
ЗАДАЧ
КОНТРОЛЬНОЙ РАБОТЫ
Задание
I.
Обозначим исследуемую функцию
у
«/(*).
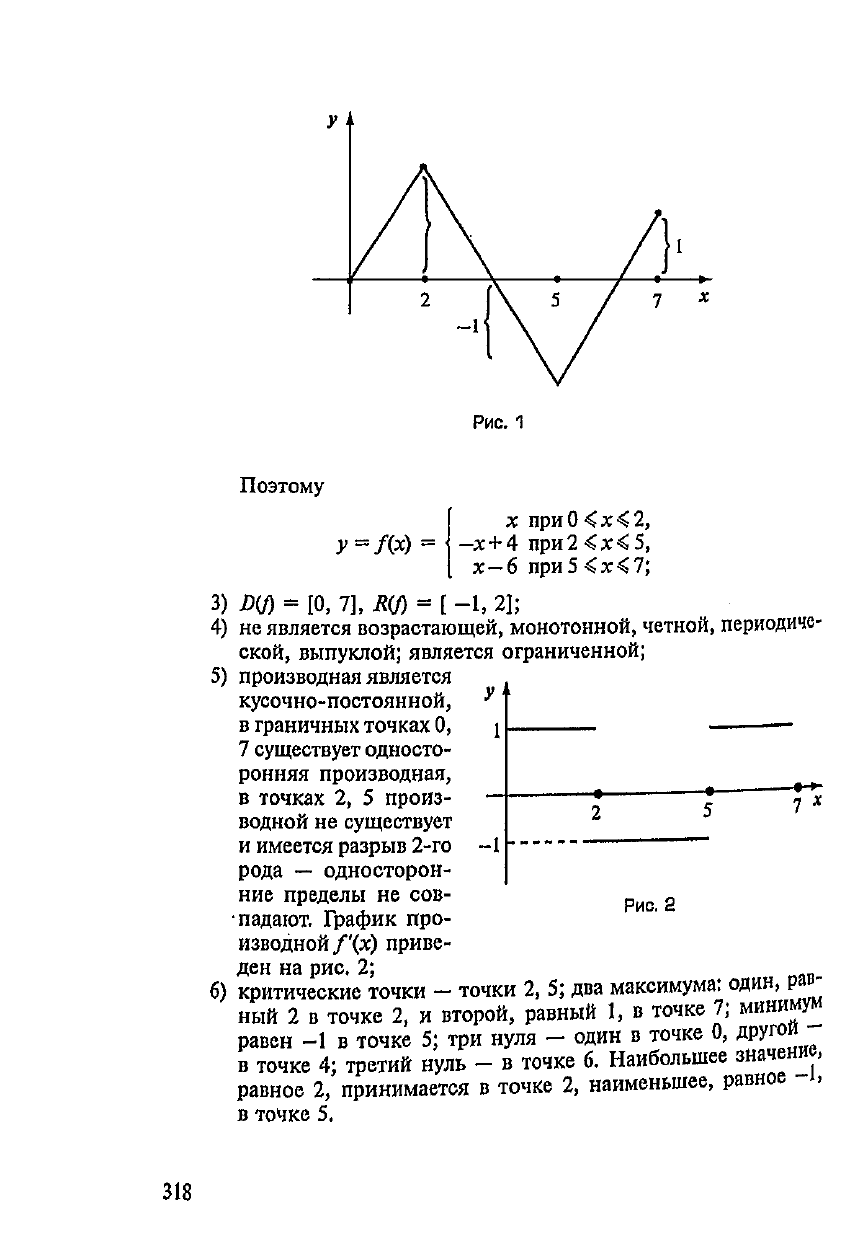
1)
график
Дх)
приведен
на
рис,
1;
2)
уравнение
пр/шой,
проходящей
через
точки
(х
0
,
^
0
)
и
(*,,
у,),
есть
(х
-
*„)/(*,
-
х
0
)
«
(у
-
у
й
)/(У
{
-
У<)
(см.
п.
1,
раздел
2.1).
317
318
Рис.
1
Поэтому
х
приО<х<2,
y=f(x)
=
-х+4
при2<#<5,
х—6
лри5<х<7;
3)
Щ
=
[0, 7],
Д/>
=
[
-1,
2];
4) не
является возрастающей,
монотонной,
четной,
периодиче-
ской, выпуклой; является ограниченной;
5)
производная является
кусочно-постоянной,
в
граничных
точках
О,
7
существует односто-
ронняя
производная,
в
точках
2,
5
произ-
водной
не
существует
и
имеется разрыв 2-го
рода
—
односторон-
ние
пределы
не
сов-
•
падают. График
про-
изводной/'(х)
приве-
ден
на
рис.
2;
6)
критические точки
-
точки
2, 5; два
максимума;
один,
р«
ный
2 в
точке
2,
и
второй,
равный
1,
в
точке
7;
минимум
равен
-1 в
точке
5; три
нуля
-
один
в
точке
0,
другой
-
в
точке
4;
третий
нуль
- в
точке
6.
Наибольшее
значение,
равное
2,
принимается
в
точке
2,
наименьшее, равное
-i,
в
точке
5.
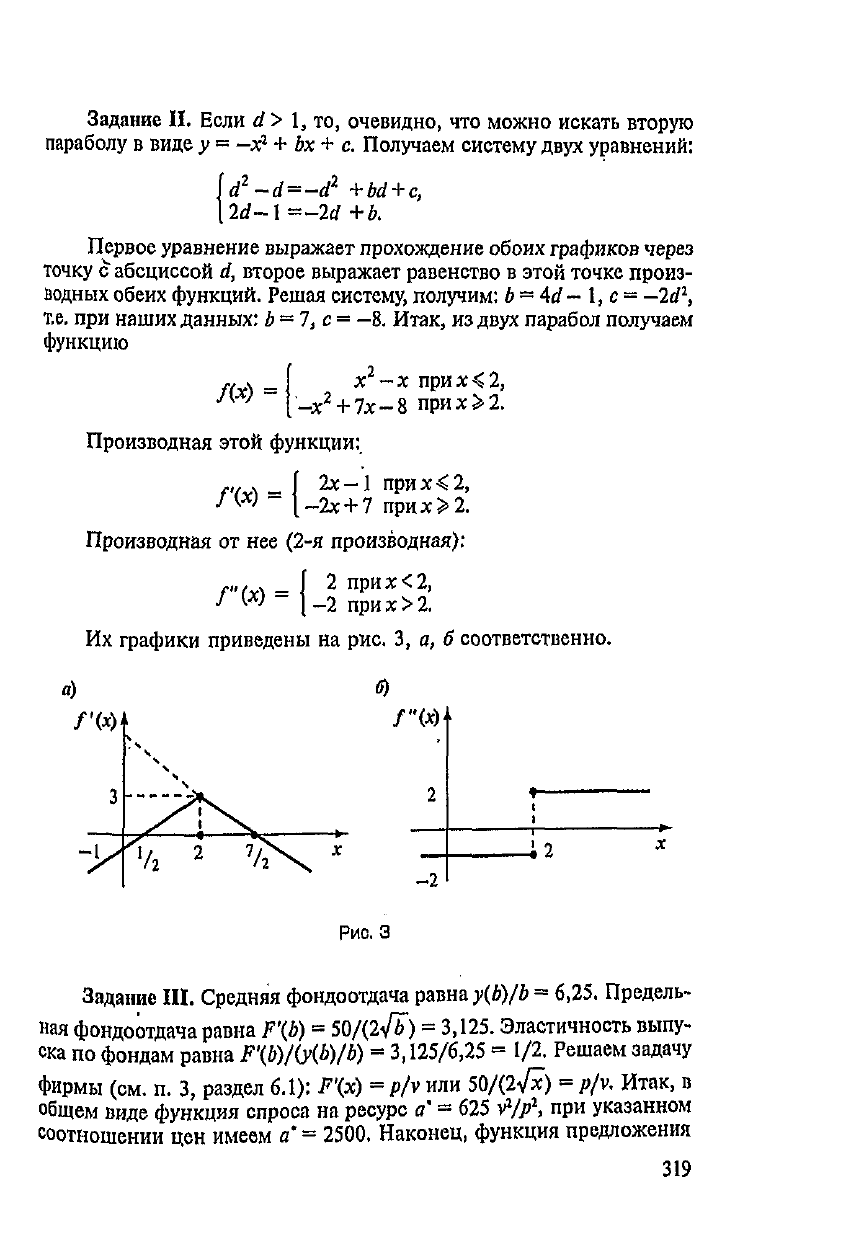
Задание
И.
Если
d > 1, то,
очевидно,
что
можно искать вторую
параболу
в
виде
у
~
—х
2
+
Ьх
+ с.
Получаем систему двух уравнений:
\4
г
-<1=-£
+
bd
+
c,
\2d-\~-2d
+b.
Первое
уравнение выражает прохождение обоих графиков через
точку
с
абсциссой
d,
второе выражает равенство
в
этой точке произ-
водных
обеих функций. Решая систему, получим;
b —
4d
—
1,
с —
—
2d
2
,
т.е.
при
наших
данных:
b
~
7, с = -8.
Итак,
из
двух парабол получаем
функцию
л-л
={
х
2
~х
прих<2,
/w
1-х
2
+
7х-8
прих>2.
Производная этой
функции:.
f
ч
\
_
J
2х
-1
при
х < 2,
'
w
-
|_2х
+
7
прил>2.
Производная
от нее
(2-я производная):
f
,,
M
- \ 2
при^<2,
/
w
|_2
прих>2.
Их
графики приведены
на
рис.
3, а,
б
соответственно.
Задание III. Средняя фондоотдача равна
у(Ь)/Ь
-
6,25.
Предель-
ная
фондоотдача
равна
РЩ
-
50/(2^)
-
3,125.
Эластичность выпу-
ска
по
фондам
равна
РЩ/(у(Ь)/Ъ)
-
3,125/6,25
-
1/2.
Решаем
задачу
Фирмы
(см.
п. 3,
раздел
6.1):
F'(x)
=
p/v или
50/(2i/x)
=
/»/v.
Итак,
в
общем виде функция спроса
на
ресурс
а'
=
625
v
2
//»
2
,
при
указанном
соотношении
цен
имеем
а'=
2500. Наконец, функция предложения
319

продукции
в
общем
виде
у'
=
50V
а'
-
1250
v/p;
для
указанного соот-
ношения
цен
у'
—
2500.
Задание
IV.
Подобная задача
достаточно
подробно
рассмотрена
в
п. 2,
раздел
6.1.
Задание
V.
Исследуем
и
построим график только
для
второй
функции
—
F(x):
1)
область определения функции:
х
я*
±1;
2)
функция
общего
вида;
3) две
точки разрыва:
х,
*=
-1,
х
2
— 1, в
обеих точках
разрывы
2-го рода;
4) две
вертикальные асимптоты:
х =
—1,
х
~
1, и две
горизон-
тальные
—
левосторонняя
у
=
0 и
правосторонняя
у
=
0;
5)
одна точка пересечения
с
осью абсцисс
— х - 0;
6)
производная
F'(x)
=
(6х
2
+
б)/(1
-
л
2
)
2
> 0, за
исключением
точек
х - ±1;
значит, есть
три
промежутка возрастания:
(-«о,
-1), (-1,
1),
(1,
оо);
экстремумов нет;
7)
поскольку
1-я
производная строго
положительна,
точек
пе-
региба нет; строим график функции (рис.
4),
320

3.
СЕМЬ
ВАРИАНТОВ ЗАДАНИЙ
К
КОНТРОЛЬНОЙ РАБОТЕ
№
вар.
1
2
3
4
5
б
7
Данные
для
задания
I
(0,
1),
(2,
-1)
(4,
6), (6, 0)
(0,0),
(1,2)
(3,-0,(5,
1)
(0,
-1),
(2, 0)
(4,
0),
(5, 2)
(0,
-2),
(2, 0)
(4,
3), (б, 0)
(0,
3),
(2,
4)
(4,
-1),
(6, -2)
(1;
4),
(2, 4)
(4,
б), (б,
0)
(0,
2),
(I,
4)
(3,
0),
(5,
-1)
II
2
3
4
5
б
7
8
III
\$х
27
5Qjx
100
3ot/;c~
81
40*
3
"
8
40*V<
16
64*
3
/'
32
9бх"
5
32
IV
Q
=
1000
л:
=1000
л
«ю
Л/=50
Q
-
2000
К
«
2000
л
=
ю
Л/=50
Q
=
4000
х=зооо
Л
«20
Л/
= 100
Q
=
4000
Я
=2000
Л-
10
Л/=40
Q«500
К
«500
Л
=10
Л/=50
0=500
К=
1000
Л
«20
Л/-
50
Q
=
1000
tf=
1200
Л
«15
Л/=
100
V
.Дл:)
=
2.x
2
—
х
Дл)
=
2/(л
+
I)
1
Дх)
= tf -
х
+
1
F(x)
=
4/(х
г
+
1)
f(x)
=
-tf
+
2x
Дх)
=
х/(£
+ 1)
Дх)
=
2^-5
Дх)
=
хУ(х
- 1)
Дх)
«
-х
1
+
х
+ б
ад
=
4/(Х*-1))
.Дх)
= -
х*
+
1х
+ 4
ад
=
2(;с*
-
1)Д
Дх)
«
л
2
-
2х
+
4
ад
=
2(1-л)/^
321
