Максимов А.И., Мошников В.А., Таиров Ю.М., Шилова О.А Основы золь-гель-технологии нанокомпозитов
Подождите немного. Документ загружается.

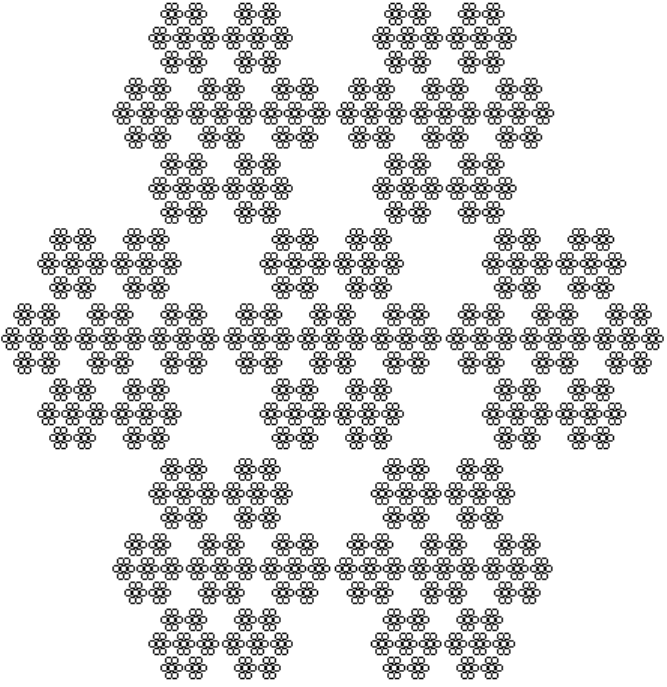
81
Рис. 3.9. Квазидвумерная проекция трехмерного
фрактального агрегата Жюльена
Очевидно, необходимо обратить особое внимание на полученную ве-
личину D. Величина D определяет, каким образом распределяется в про-
странстве масса сформированного агрегата. Для случая плотно располо-
женных сфер в трехмерном пространстве справедливым является соотно-
шение D = 3. Для плоскости, образуемой плотно уложенными сферами, D
= 2, а для сфер, выстроенных в одну линию, D = 1. Таким образом, выше-
приведенное определение D совпадает с обычным определением размер-
ности для сплошных структур. Естественным является то обстоятельство,
что плотность таких тел не зависит от их размера.
Если предположить, что каждая сфера имеет единичную массу, тогда
для плотности (r) фрактального агрегата в трехмерном пространстве по-
лучаем (r) = Br
D – 3
, где B = 3A/4.
Полученный результат свидетельствует о необычном поведении
плотности полученного трехмерного агрегата при изменении его размеров.
Плотность такого агрегата не остается постоянной при возрастании разме-
82
ров, а уменьшается. Для фрактала бесконечных размеров значение плотно-
сти стремится к нулю. Это – один из основных признаков массового фрак-
тала.
Физически это означает, что при рассмотрении все больших и боль-
ших частей фрактала мы учитываем пустоты все больших и больших раз-
меров. Как видим, для фрактала характерно наличие пустот всех размеров:
от пустоты с размерами порядка первичных частиц до пустоты размерами
порядка фрактального агрегата. Это также характерный признак массового
фрактала.
Отметим, что (r) представляет собой распределение плотности веще-
ства вокруг какой-либо одной случайно выбранной частицы. То есть это
так называемая двухчастичная корреляционная функция. Эта функция дает
для выбранной частицы вероятность найти другую частицу на расстоянии
r от первой (выбранной) частицы. Таким образом, для фрактала корреля-
ционная функция уменьшается с увеличением расстояния по степенному
закону r
D–3
. Заметим, что скорость такого уменьшения становится
меньшей с ростом D и при D = 3 величина (r) теряет зависимость от r.
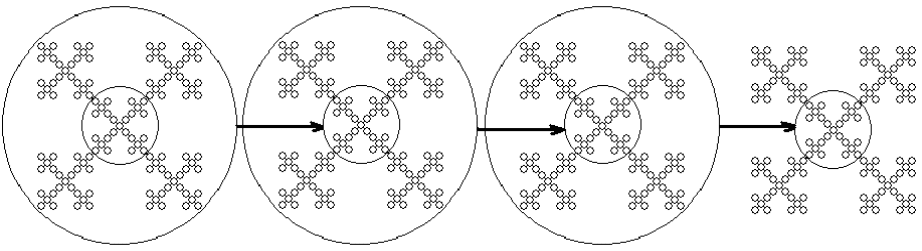
Рис. 3.10. Иллюстрация свойства самоподобия двухмерного неупорядоченного агрегата
Еще одним замечательным свойством рассмотренного фрактала явля-
ется свойство его самоподобия или самоповторяемости. Поскольку это
свойство легче наблюдать на двумерных объектах, рассмотрим такой же
вид фрактальной структуры, но построенной на плоскости из дисков (рис.
3.10). В данном случае внутри окружности радиуса
p
r 3
(p = 0; 1; 2…)
будет содержаться уже
p
rn 5)(
частиц, а фрактальная размерность будет
равна D = ln 5/ln 3 = 1.465. Такой агрегат, построенный при очень большом
числе итераций так, что отдельные частицы не различимы для невоору-
женного глаза, представлен в левой части рис. 3.10. Центральная часть аг-
83
регата, после увеличения в 3 раза, показана правее. Видно, что увеличен-
ная часть очень похожа на весь агрегат. Это происходит потому, что наш
глаз не может разрешить пространственное расстояние меньше некоторой
величины. В результате создается впечатление, что обе фигуры имеют
идентичную структуру, составленную из сфер радиуса l. На самом деле
каждая из таких видимых сфер содержит гораздо большее число частиц,
чем имеется в первоначальном агрегате (в 3
D
раз больше). Таким образом,
как отмечалось ранее, в малом фрагменте детерминированного фрактала
содержится информация обо всей его структуре.
Рассмотренные выше фрактальные объекты как чисто математические
представления являются бесконечными объектами. То есть фрактальные
агрегаты имели бесконечные размеры и были сделаны из бесконечно ма-
лых первичных частиц. Но на практике всегда имеется два естественных
(нижний и верхний) масштаба так называемого обрезания размеров (рис.
3.8). Первый (нижний) определяется тем, что размеры первичных частиц a
не бесконечно малы, а имеют какую-то конечную величину. В то же время,
второй (верхний) масштаб определяется тем обстоятельством, что размер
самого агрегата не является бесконечным, а ограничивается величиной L.
Обычно свойство n(r) ~ r
D
справедливо только в пределах изменения r, оп-
ределяемых неравенством a < r < L. Именно это неравенство и определяет
различие между математическими фракталами (бесконечной величины) и
физическими фракталами, величина которых конечна. Считается, что
можно говорить о том, что мы имеем дело с фрактальным агрегатом, в том
случае, если размер первичных частиц a и размер агрегата L различаются
хотя бы на порядок (должно быть L/a > 10).
Описанный способ построения фракталов далеко не всегда может
быть реализован в естественных процессах агрегации. Маловероятно, что-
бы полученные при этом агрегаты имели точно такую же макроскопиче-
скую симметрию, как на рис. 3.9 и 3.10, поскольку в процессах естествен-
ной агрегации всегда присутствует элемент случайности. Вводя такой эле-
мент в построение фракталов, можно получить случайные фракталы. При
этом основное их отличие от детерминированных фракталов будет состо-
ять в том, что для случайных фракталов вышеприведенные правила ока-
жутся справедливыми только после усреднения по всем статистически не-
зависимым реализациям объекта. Рисунок 3.8 иллюстрирует свойство са-
моподобия для случайного двумерного агрегата. Как видим, фрактальные
84
агрегаты не идентичны. Они реализуются в разных статистически эквива-
лентных конфигурациях. Подобным образом зависимость n(r) от r не стро-
го линейна в логарифмических координатах. Такая линейность получается
после усреднения n(r) по многим агрегатам, состоящим из одинакового
числа частиц и построенным по одинаковому правилу.
Необходимо отметить, что имеются обобщения концепции фракталов
на случай несамоповторяющихся структур. К последним относится, в ча-
стности, самоаффинный фрактал, который представляет структуру, инва-
риантную после одновременного, но количественно разного изменения
масштаба вдоль разных направлений в пространстве. Для полной характе-
ристики свойств самоаффинного фрактала необходимо использовать уже
не одну, а большее число экспонент (т. е. степенных показателей). Таким
образом, для самоаффинного фрактала существует столько фрактальных
размерностей, сколько независимых направлений в пространстве (в случае
трехмерного пространства – три).
Дальнейшим обобщением фрактала является мультифрактал, который
может характеризоваться бесконечным числом независимых фрактальных
размерностей [
92
].
Отметим, что мы будем ограничиваться в основном рассмотрением
"массовой" фрактальной размерности D, а именно той, которая описывает
изменение массы в зависимости от изменения размера, и поверхностной
фрактальной размерности D
s
. Однако это не единственные параметры, ис-
пользуемые для описания фрактальных структур. Имеются другие виды
фрактальных размерностей. К их числу относятся, в частности, следую-
щие: размерность распространения (характеризует свойства связанности в
агрегате) и специальная размерность, характеризующая динамические
свойства фрактала.
В пористых материалах, какими часто бывают продукты золь-гель-
синтеза, могут наблюдаться как массовые, так и поверхностные фракталы
[
93
]. Образование массовых фракталов возможно в двух случаях: при ма-
лой и большой степени пористости. В первом случае массовый фрактал
образуется пористой средой, а во втором – "скелетом" пористого материа-
ла. Подробнее к этому вопросу вернемся при рассмотрении элементов тео-
рии перколяции. Здесь же отметим, что при пористости, не соответствую-
щей этим предельным случаям, массовые фракталы не образуются. Однако
при этом материал может проявлять свойства поверхностного фрактала. В
85
частности, в случае пористой среды для числа пор радиуса R справедлива
скейлинговая (масштабная) зависимость типа N(ν) ν
–(Ds+1)
(ν = R/R
max
,
R
max
– максимальный радиус пор, D
s
– фрактальная размерность поверх-
ностного фрактала), а общая поверхность всех пор с радиусами в пределах
от R до R
max
изменяется в соответствии со степенным законом S(ν) ν
–
(Ds–2)
, т. е. при R 0 величина S(ν) при 2 < D
s
< 3 (условие фракталь-
ности поверхности). Таким образом, фрактальная размерность поверхно-
стного фрактала изменяется в пределах от 2 до 3. Чем выше D
s
, тем более
грубая поверхность фрактального объекта. D
s
= 2 соответствует фракталь-
ному объекту с гладкой поверхностью, а при D
s
→ 3 – объекту с наиболее
грубой (шероховатой) поверхностью.
Прежде чем перейти к рассмотрению фрактальных агрегатов, возни-
кающих в эксперименте еще раз вернемся к зависимости (r) = Br
D – d
, где
D – массовая фрактальная размерность, d – размерность пространства, в
котором существует фрактал. Отметим, что даже для регулярных (детер-
минированных) фракталов эта зависимость не соблюдается точно для лю-
бых непрерывно изменяющихся значений r. Иными словами, функция (r)
осциллирует, а значения (r) соответствуют приведенной зависимости при
переходе на новый уровень масштабирования (значения r, при которых на-
блюдается самоподобие).
3.5. Физические фракталы
Физические объекты со структурой, обладающей фрактальными свой-
ствами, получили название "физические фракталы". При изучении физиче-
ских фракталов важно не только установить характер этих структур, но и
понять внутренний механизм, обеспечивающей такое строение.
Большая группа физических фракталов связана с агрегационными яв-
лениями, такими как осаждение, фильтрация, электролиз, флоккуляция и
агрегация. Такие фракталы называют фрактальными агрегатами, или фрак-
тальными кластерами.
Продукты золь-гель-процессов, которые возникают благодаря агрега-
ционным явлениям, в результате подавления дальнодействующих сил от-
талкивания между частицами в локальной области, относятся к этой груп-
пе фракталов.
86
Взаимное сближение частиц зависит от характера движения каждой из
них и в значительной степени может определяться закономерностями бро-
уновского движения. Как было показано в 3.2, траектория частицы при
броуновском движении является фракталом. Это послужило предпосылкой
для создания компьютерных моделей роста фрактального агрегата. Первая
модель диффузионно-лимитируемой агрегации (DLA) была создана Вит-
теном и Сэндером в 1981 г. Хорошее согласие модели с рядом эксперимен-
тов стимулировало развитие компьютерного моделирования роста фрак-
тальных кластеров. Далее мы рассмотрим основные модели. Здесь же от-
метим, что модельные представления об образовании фрактальных агрега-
тов хорошо описывают и другие объекты, не относящиеся к продуктам аг-
регационных явлений (более того, не являющиеся физическими телами,
например явления диэлектрического пробоя, образования молнии, смеше-
ния жидкости). Природа этих фракталов совсем иная, но из-за близости
математических закономерностей эти физические фракталы также тради-
ционно относят к группе фрактальных агрегатов. Особенности физической
природы различных видов фрактальных агрегатов подробно рассматрива-
ются в [14].
Из вышеизложенного следует, что при соблюдении определенных ус-
ловий продуктами золь-гель-технологии могут быть физические объекты,
соответствующие фрактальным агрегатам. Но это не означает, что любой
несплошной физический объект, если он получен в золь-гель-процессе, яв-
ляется фракталом. С другой стороны, крайне важно понимание возмож-
ности реализации получения фрактальных структур и нахождения эффек-
тивных технологических приемов управления фрактальной размерностью
(как массовой D, так и поверхностной D
s
). Это позволяет целенаправленно
вводить комплекс приемов по созданию новых материалов с уникальными
свойствами для приборов нового поколения.
Исследования по установлению закономерностей изменения свойств
материалов от значения фрактальной размерности еще находятся на на-
чальной стадии. Но влияние фрактальной размерности (а следовательно,
развитости поверхности) на некоторые свойства (адсорбционную способ-
ность, каталитическую активность, селективную проницаемость и др.) на-
столько очевидны, что не требуют особых доказательств.
Продуктом золь-гель-технологии (при создании нанокомпозитов) мо-
гут быть и объекты с фрактальной структурой, но не относящиеся к группе
87
фрактальных агрегатов. Это так называемые перколяционные кластеры.
Возникновение перколяционных кластеров является предметом анализа в
теории перколяции. Теория перколяции (от англ. percolation – протекание,
просачивание) в русскоязычной литературе часто называется теорией про-
текания.
Физическую сущность явления перколяции можно качественно пояс-
нить, воспользовавшись схемой, изображенной на рис. 2.4. Представим,
что иммобилизованные частицы резко отличаются по физическим свойст-
вам от окружающей матрицы. Например, частицы обладают металличе-
ской или полупроводниковой проводимостью в диэлектрической матрице.
Тогда с увеличением их концентрации х при превышении некоторого зна-
чения х
с
образуется проводящий кластер (перколяционный), пронизываю-
щий весь объем физического объекта. Иными словами, существует так на-
зываемый порог протекания х
с
, при котором физические свойства объекта
резко изменяются. Установлено, что в неупорядоченных системах (суще-
ствующих в 3-мерном пространстве) со случайным распределением частиц
(например, проводящих и диэлектрических) перколяционный кластер име-
ет фрактальную структуру с размерностью D, равной 2.5.
Применение модельных представлений перколяционных кластеров
для создания высокоселективных газочувствительных адсорбционных сен-
соров на сероводород рассмотрено в [67]. Необходимо еще раз подчерк-
нуть принципиальные физические различия между фрактальными агрега-
тами и перколяционным кластером. Фрактальные агрегаты начинают обра-
зовываться при сколь угодно малых концентрациях частиц, в то время как
перколяционный (стягивающий) кластер возникает только при превыше-
нии концентрации, соответствующей порогу протекания.
3.6 Основные понятия теории перколяции
Первая научная работа по теории перколяции была опубликована в
1957 году (С. Бродбент и Дж. Хаммерсли). Теоретический подход был на-
мечен при решении узкой практической задачи для описания защитных
функций фильтров противогаза. Во время эксплуатации развитая поверх-
ность адсорбента связывает газовые молекулы, блокируются адсорбцион-
ные центры, и возникают "кластеры", которые уже не способны захваты-
вать молекулы газа. Эти кластеры увеличиваются в размерах, и в некото-
88
рый момент времени возникает стягивающий кластер. Другими словами
возникает путь, по которому молекулы газа способны просачиваться (per-
colation). Эту критическую ситуацию можно охарактеризовать долей бло-
кированных центров [
94
]. В настоящее время теория перколяции является
главным инструментом в теории неупорядоченных систем [
95
]. При этом в
[95] атомно-неупорядоченные твердые тела разделяют на три группы:
1. Системы, в которых атомы не образуют кристаллической решетки с
дальним порядком, но расположение ближайших соседей приблизительно
упорядочено (аморфные материалы)
2. Неупорядоченные сплавы и твердые растворы, в которых узлы об-
разуют упорядоченную решетку, а атомы различных компонентов распре-
делены по узлам случайным образом.
3. Кристаллы, в решетке которых имеются примесные атомы и точеч-
ные дефекты, нарушающие периодичность решетки.
Нанокомпозиты и пористые материалы также являются объектами,
изучаемыми методами теории перколяции. Часто образование перколяци-
онного стягивающего кластера называют геометрическим фазовым пере-
ходом. Смысл этого определения легко проиллюстрировать для композита,
состоящего из элементарных ячеек двух типов. Пусть ячейки первого типа
являются проводниками, а ячейки второго типа – идеальными диэлектри-
ками. Тогда увеличение доли ячеек 1-го типа в исходном материале из яче-
ек 2-го типа позволяет изменять электрические свойства системы от пол-
ностью изоляционных до полностью проводящих. Но этот переход не бу-
дет равномерно растянут во всем диапазоне изменения концентрации про-
водящих ячеек. При малых концентрациях проводящих ячеек они изоли-
рованы друг от друга и от электродов диэлектрическими ячейками. При
некоторой доле x
с
, называемой порогом протекания, возникает стягиваю-
щий кластер, т.е. появляется проводимость. Вблизи порога протекания x
c
тело разбивается на части, обладающее различными свойствами. Геомет-
рия этих разбиений каждый раз приобретает новые случайные формы, но
значения порога протекания для тел бесконечных размеров строго опреде-
лены и зависят от симметрии и размерности пространства.
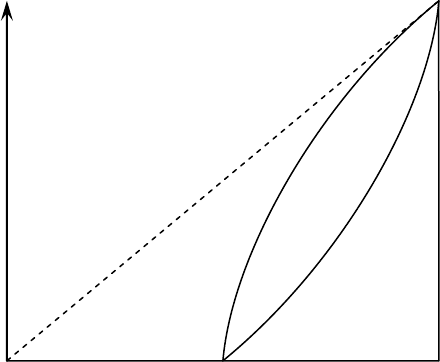
Если обозначить через P(x) – долю проводящих ячеек, входящих
только в стягивающий (бесконечный) кластер, по отношению к общему
количеству ячеек то зависимость P от общей доли проводящих ячеек, име-
ет вид, приведенный на рис. 3.11. Там же построена приведенная зависи-
89
мость проводимости бесконечного кластера (x)/(1) от доли проводящих
ячеек x.
Рис. 3.11. Зависимости мощности бесконечного кластера P(x) и приведенной
проводимости бесконечного кластера (x)/(1) от доли проводящих ячеек в системе
Бесконечный стягивающий кластер P(x) появляется (по определению)
при значении x = x
c
и приобретает максимальное значение, равное 1, при x
= 1.
Легко понять и пределы изменения значений (x)/(1). Проводимость
(x) возникает при x = x
c
и не может быть больше, чем проводимость (x)
системы, состоящей только из проводящих ячеек. Как видно из рис. 3.11
для значений x
c
< x < 1 не все проводящие ячейки, входящие в структуру
бесконечного кластера участвуют в увеличении проводимости (значение
P(x) выше, чем (x)/(1)). Для объяснения введем понятие ячеек, принад-
лежащих скелету бесконечного кластера и ячеек, лежащих на "мертвых
концах" (рис. 3.12) [95]. Для ячеек, находящихся на "мертвых концах" воз-
можно удаление в бесконечность только в одном направлении. Такие
ячейки, входя в состав бесконечного кластера, увеличивают значение P(x),
но не влияют на значение (x)/(1).
С материаловедческой точки зрения применения теории перколяции
представляет интерес для анализа свойств композитов, состоящих не толь-
ко из "проводящих" и "диэлектрических" ячеек, но и компонентов, состав-
ляющих пары "проводник-сверхпроводник", "парамагнетик-магнетик",
"параэлектрик-сегнетоэлектрик" и др.
P(x)
0
(x)/(1)
P(x)
1
x
c
(x)/(1)
1
90
Рис. 3.12. Иллюстрация мертвых концов бесконечного кластера
С теоретической точки зрения модели перколяции разбивают на "ре-
шеточные" и "непрерывные". Решеточные задачи в свою очередь разделя-
ются на задачи "узлов" (site problem) и "связей " (bond problem) и смешан-
ные задачи (site-bond-percolation) [
96
].
Задача узлов сводиться к нахождению порога протекания на решетке с
заданными параметрами (симметрия, размерность пространства). При этом
анализируются кластеры, образованные контактирующими узлами – сфе-
рами (например, "проводящими") при замещении исходных "непроводя-
щих" сфер.
В задаче связей все исходные узлы – сферы, расположенные в задан-
ной решетке, считаются проводящими, но контакт между ними зависит от
наличия связей. В задаче связи блокировка узла в целом осуществляется
при разрыве всех связей.
Разработаны принципы геометрии "покрывающих" решеток, демонст-
рирующих соотношение между значениями порогов протекания в задаче
связей x
c
(св) и задаче узлов x
c
(уз).
x
c
(св) x
c
(уз).
Для прекращения протекания необходимо полностью блокировать оп-
ределенную долю узлов, разорвав все связи, при этом остальная часть уз-
лов будет иметь некоторые разорванные связи. К настоящему времени
найдены значения порогов протекания для решеток в пространствах раз-
личной размерности d (d = 1, 2, 3 и др.), включая d = (решетки Бете). Ре-
шетки в пространствах d > 3, например d = 6, представляют интерес для
оценки перколяционных явлений тензорных физических величин.
В табл. 3.1 приведены значения порогов протекания и связанных с
ними величин для двумерных и трехмерных решеток [95].
Таблица 3.1.
Пороги протекания и связанные с ними значения для двумерных и трехмерных решеток
