Макаров Е.Г. Сопротивление материалов
Подождите немного. Документ загружается.


max
τ
max
τ
0=τ
b<h
h
b
Рис. 6.14. Распределение касательных напряжений в прямоугольном сечении
Максимальные касательные напряжения
max
τ
возникают в середине длинной
стороны прямоугольного сечения.
В середине короткой стороны
max
τ
γτ
=
⋅ .
Момент инерции и момент сопротивления при кручении рассчитываются по
формулам
3
к
J
hb
α
= и ,
2
к
Whb
β
=
где коэффициенты
α
,
β
и
γ
определяются из справочника в зависимости от
отношения сторон прямоугольника
h
b
, где — большая сторона прямоугольника.
Значения этих коэффициентов приведены в таблице 6.1.
h
Таблица . 6.1 Коэффициенты для расчета на кручение стержней прямоугольного сечения
h/b
α β γ
h/b
α β γ
1 0,141 0,208 1,000 4 0,281 0,282 0,745
1,5 0,196 0,231 0,859 6 0,299 0,299 0,743
2 0,229 0,246 0,795 8 0,307 0,307 0,743
2,5 0,249 0,256 0,766 10 0,313 0,313 0,743
3 0,263 0,267 0,753
∞
0,333 0,333 0,743
Тонкостенные сечения открытого профиля
К таким сечениям можно отнести прокатные профили: уголок, швеллер, двутавр,
которые можно представить в виде набора прямоугольников. Для них
Момент инерции
3
к
3
bh
J =η
∑
, момент сопротивления
к
к
max
J
W
b
= ,
где и — ширина и высота каждого прямоугольника, входящего в состав
сечения,
η — поправочный коэффициент.
b h
Для уголка , для швеллера
1η= 1, 12
η
= , для двутавра 1, 2
η
= .
61

открытый профиль
закрытый профиль
Рис. 6.15 Сечения стержней закрытого и открытого профиля
Тонкостенные сечения закрытого профиля
Примерами таких сечений являются кольцевое сечение и коробчатое сечение,
состоящее из набора прямоугольников. Для них
Момент инерции
2
сред
к
S
4
dS
A
J
δ⋅
=
δ
∫
v
, момент сопротивления
к min сред
2WA
=
δ⋅ ,
где — длина средней линии тонкостенного сечения, — площадь,
ограниченная средней линией сечения,
S
сред
A
δ
— толщина сечения.
Если толщина сечения постоянная, то
min сред
2
к
WA=δ , и
2
сред
к
4 A
J
S
δ⋅
=
.
Следует отметить, что жесткость и прочность тонкостенных сечений закрытого
профиля неизмеримо больше, чем сечений открытого профиля. Так при нанесении
прорези на трубу при
0.1
d
D
= жесткость трубы уменьшается почти в сто раз.
62
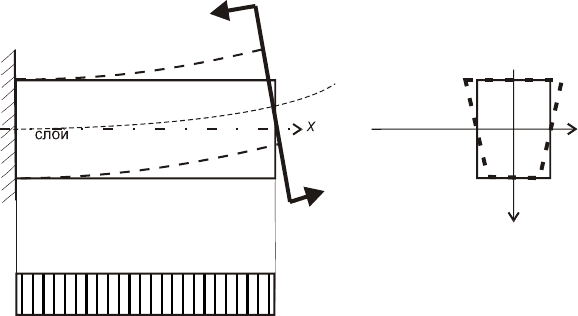
Глава 7. Плоский поперечный изгиб
Изгибом называется деформация, в процессе которой продольная ось бруса
искривляется.
Стержень (прямолинейный брус), работающий на изгиб, называется балкой
.
При упругой деформации продольную ось балки (линию, соединяющую центры
тяжести поперечных сечений,) называют
упругой линией балки.
Изгиб бывает
плоским и пространственным. При плоском изгибе упругая линия
балки — плоская кривая, при пространственном изгибе — пространственная кривая.
В этой главе рассмотрим лишь плоский поперечный изгиб. Пространственный изгиб
бруса будет рассмотрен в главе 10, как частный случай сложного сопротивления.
Поперечным называется изгиб балки, вызванный силами, перпендикулярными
продольной оси балки. Это условие необходимо, чтобы изгиб был поперечным, но
недостаточно. Дополнительное условие будет сформулировано в разделе 7.1.
При плоском поперечном изгибе в поперечных сечениях балки под действием
внешних (поперечных) сил возникают два внутренних усилия: поперечная сила
Q и
изгибающий момент
M
, которые определяются методом сечений. Определение
внутренних усилий при изгибе и построение эпюр и
Q
M
рассмотрено в главе 3
(разделы 3.3 и 3.4). В этой главе рассмотрим напряжения в поперечных сечениях
балки и перемещения балки при изгибе.
7.1 Нормальные напряжения при изгибе балки
Под действием изгибающего момента
M
в поперечных сечениях балки возникают
нормальные напряжения
σ
, под действием поперечной силы
Q
— касательные
напряжения
τ
. Чтобы упростить задачу определения напряжений, рассмотрим
чистый изгиб балки.
Чистым называется изгиб, при котором в поперечных сечениях балки отсутствует
поперечная сила.
с
ж
а
т
и
е
рас
т
я
ж
е
н
ие
М
0
М
0
М
0
y
z
нейтральный
нейтральная
ось
σ=0
Рис. 7.1. Чистый изгиб балки
Пример чистого изгиба балки приведен на рис.7.1. Сплошной линией показан вид
балки до деформации, пунктиром — после деформации. Под действием пары сил
M
балка изгибается. При этом верхние волокна сжимаются
ε
<
0, а нижние
растягиваются
ε
>0. В таком случае где-то в средней части балки есть волокна, где
деформация
ε
=
0 , а, следовательно, и напряжение
σ
=
0.
Слой волокон, в котором отсутствует нормальное напряжение, называется
нейтральным
.
След пересечения нейтрального слоя с плоскостью поперечного сечения называется
нейтральной осью
.
Форма поперечного сечения балки при изгибе также изменяется. В области сжатых
волокон сечение становится шире, в области растянутых — уже, так как продольная
и поперечная деформации связаны коэффициентом Пуассона
попер прод
ε
με
=
−⋅ .
При расчете балки на изгиб будем считать, что справедливы все гипотезы из
раздела 1.9. Из них выделим две гипотезы, которые будут использованы при выводе
формулы нормальных напряжений при изгибе.
Гипотеза отсутствия боковых давлений — волокна друг на друга не давят. В
силу этой гипотезы при чистом изгибе волокна балки испытывают растяжение-
сжатие
y
z
σ
στ
=
==0
x
σ
σ
=
, следовательно справедлив закон Гука при
растяжении-сжатии
E
σ
ε
=⋅
63
Гипотеза плоских сечений — сечения плоские до деформации остаются плоскими
после деформации.
Как и при кручении вывод конечной формулы состоит из трех частей.
Геометрический анализ
.
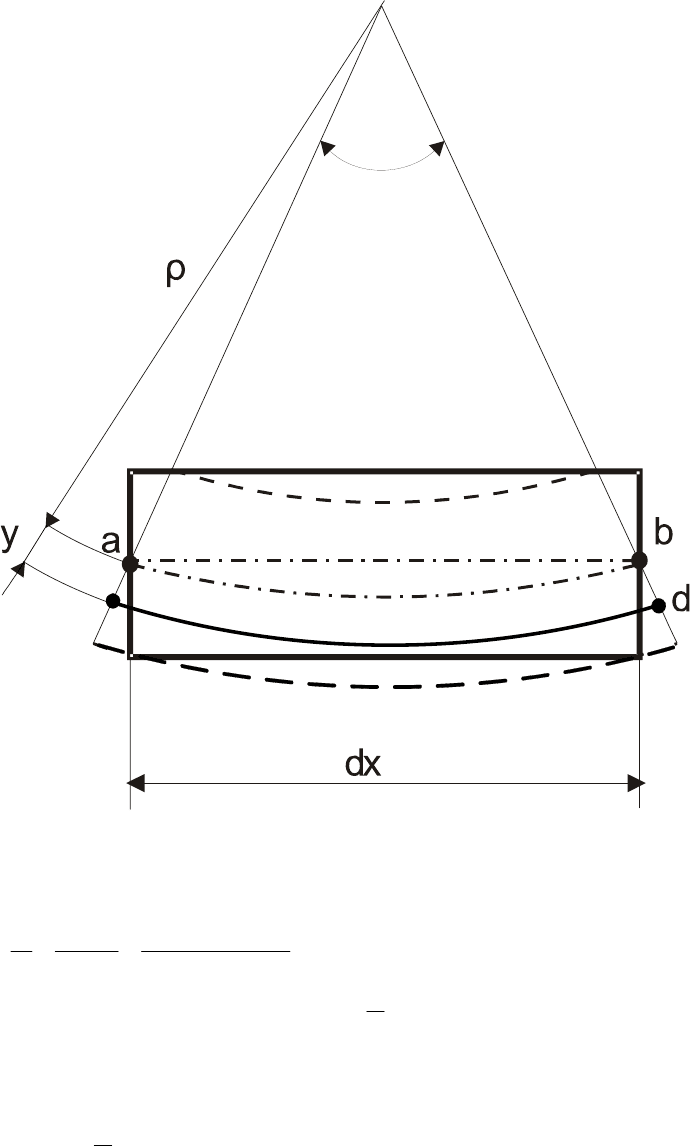
Вырежем из балки элемент длиной
dx и рассмотрим его деформацию (рис. 7.2).
Предположим, что волокно ab — след нейтрального слоя, его положение еще
предстоит определить. В нейтральном слое волокна не деформируются
ε
=0 и
σ
=0.
На некотором расстоянии y от ab возьмем волокно cd и рассмотрим его
деформацию
()
ab dx d
cd y d
ρ
θ
ρ
θ
==⋅
=+⋅
,
где
ρ
— радиус кривизны нейтрального слоя.
с
d
θ
Рис. 7.2. К определению деформации при изгибе
Деформация волокна cd на расстоянии от нейтрального слоя y
Δ−ρ+⋅θ−ρ
ε= = =
ρ⋅ θ
()lcdab
θ
y
dd
lab d
.
Откуда после упрощения получаем
y
ε
ρ
=
(7.1).
Физический анализ
Справедлив закон Гука. Следовательно, в силу гипотезы отсутствия боковых
давлений
y
E
E
σε
ρ
=⋅= . (7.2).
Формула есть, но пользоваться ею нельзя, так как не известен радиус кривизны
нейтрального слоя . Чем больше нагрузка, тем меньше радиус кривизны. Найдем
связь между ними.
ρ
64
Статический анализ. Изгибающий момент в сечении вызывает появление
нормальных напряжений. Связь между ними устанавливает условие эквивалентности
(1.3).
z
A
M
ydA
σ
=⋅
∫
.
С учетом (7.2)
2
z
A
Ey E
z
M
dA J
ρρ
==
∫
, (7.3),
где
2
z
A
Jy
dA=
∫
.
Из выражения (7.3) находим кривизну балки
1
z
z
M
E
J
=
ρ⋅
(7.4).
Подставляя (7.4) в (7.2) получаем
z
z
M
E
y
EJ
σ
=
⋅
⋅
или окончательно
z
z
M
y
J
σ
= (7.5).
Формула (7.5) выведена при чистом изгибе балки. При плоском поперечном изгибе
гипотеза плоских сечений несправедлива и полученная формула дает ошибку.
Однако при отношении длины балки к высоте поперечного сечения
10
l
h
>
погрешность расчета не превышает 5% , что позволяет использовать полученную
формулу при плоском поперечном изгибе длинных и тонких балок.
Завершая статический анализ задачи, рассмотрим еще два условия эквивалентности
(1.2) и (1.3).
A
N
dA
σ
=⋅
∫
(7.6).
Так как при изгибе нет продольных усилий, то
0N
=
. Подставим выражение (7.5) в
(7.6)
0
zz z
z
zz z
AA
MM M
NydAydAS
JJ J
=⋅=⋅==
∫∫
,
где — статический момент сечения относительно нейтральной оси.
Изгибающий момент
z
A
SydA=⋅
∫
z
M
и момент инерции
z
J
не могут быть равны нулю, поэтому
. Следовательно, нейтральная ось проходит через центр тяжести сечения
.
0S =
z
По условию эквивалентности (1.3)
M
y
A
zdA
σ
=⋅⋅
0
y
M =
∫
. (7.7).
Но , так как рассматриваем плоский изгиб балки. Тогда, подставляя в
условие (7.7) выражение (7.5), получаем
0
yy
zz z
AA
M yzdA yzdA J
JJ J
=⋅⋅=⋅⋅=
∫∫
zz z
z
MM M
=
yz
,
где
A
J
yzdA=⋅⋅
∫
0
yz
J = y z
— центробежный момент инерции сечения. Следовательно
, а оси и являются главными осями инерции сечения балки.
Теперь можно сформулировать дополнительное условие существования плоского
изгиба.
Изгиб является плоским
,
если все силы лежат в одной из главных плоскостей
инерции балки, то есть в плоскости, проходящей через одну из главных осей инерции
сечения и продольную ось балки.
7.1.1. Условие прочности при изгибе
Нормальные напряжения
σ
при изгибе в соответствии с формулой (7.5)
распределяются по линейному закону (рис. 7.3). На уровне нейтральной оси при
0y = 0
σ
= . В волокнах максимально удаленных от нейтральной оси, то есть на
поверхности балки возникают максимальные напряжения
max
σ
в области
растянутых волокон и минимальные напряжения
min
σ
в области сжатых волокон.
65

Y
Z
σ
=
0
min
σ
max
σ
Рис. 7.3. Нормальные напряжений в поперечном сечении балки при изгибе
Условие прочности в сопротивлении материалов имеет вид
[
]
max
σ
σ
≤ .
Запишем выражение для
max
σ
max max
max max
zz
MM
y
JW
σ
==,
где
max
z
z
J
W
y
= — момент сопротивления при изгибе.
Окончательный вид условия прочности
[]
max
max
z
M
W
σ
σ
=≤. (7.8).
Запишем моменты сопротивления для наиболее часто используемых сечений.
Для балки прямоугольного сечения
3
12
z
Jbh=
32
max
12 2 6
z
z
Jbhbh
W
yh
== =
,
Для балки круглого сечения
4
64
z
Jd
π
=
=
max
2
y
d
43
3
0,1
64 2 32
z
dd
Wd
d
ππ
==≈,
Для балки кольцевого сечения
dD
α
=
,
4
(
1
)
64
z
D
J
4
π
=
−α ,
43
1
(
1
)(
1
)
64 2 32
z
DD
W
D
4
4
ππ
=−α⋅=−α
.
Для стальных конструкций прочность материала на растяжение и на сжатие
одинакова. Однако у некоторых материалов она различна.
У чугуна предел прочности на сжатие в 4 раза больше, чем на растяжение.
У дерева, наоборот, прочность на растяжение в 2 раза больше, чем на сжатие.
В таких случаях иногда приходится проверять два условия прочности: на растяжение
и на сжатие.
y
m
a
x
Р
а
с
т
.
y
m
a
x
С
ж
а
т
.
F
Рис. 7.4. Изгиб чугунного рельса
Рассмотрим чугунный рельс, лежащий на двух опорах, нагруженный посередине
силой (рис. 7.4). Пример не очень корректный, так как в настоящее время используют
стальные рельсы. Кроме того, рельс, лежащий на шпалах, надо рассматривать как
балку на упругом основании, а это совсем другой расчет.
66
Под действием силы
F
рельс прогибается. Верхние волокна сжимаются, нижние
растягиваются. Так как на сжатие прочность чугуна выше, чем на растяжение,
желательно, чтобы сжимающие напряжения в балке были больше, чем
растягивающие. Это достигается формой поперечного сечения рельса. Центр тяжести
рельса смещен вниз в сторону массивного основания
Для чугунного рельса надо делать две проверки на прочность. Отдельно для сжатых и
для растянутых волокон. Для сжатых
[]
max в.сжат
сжат сжат сжат
n
z
M
y
J
σ
σσ
=≤=.
Для растянутых волокон
в.раст
max
раст раст раст
n
z
M
y
J
σ
σσ
⎡⎤
=≤=
⎣⎦
.
7.1.2. Рациональная форма поперечного сечения
Рассмотрим балку прямоугольного сечения. Нормальные напряжения
распределяются по сечению по линейному закону. Максимальные напряжения
действуют на поверхности балки. На нейтральной оси (на уровне центра тяжести)
σ
=0. Другими словами вблизи центра тяжести сечения материал балки всегда
недогружен.
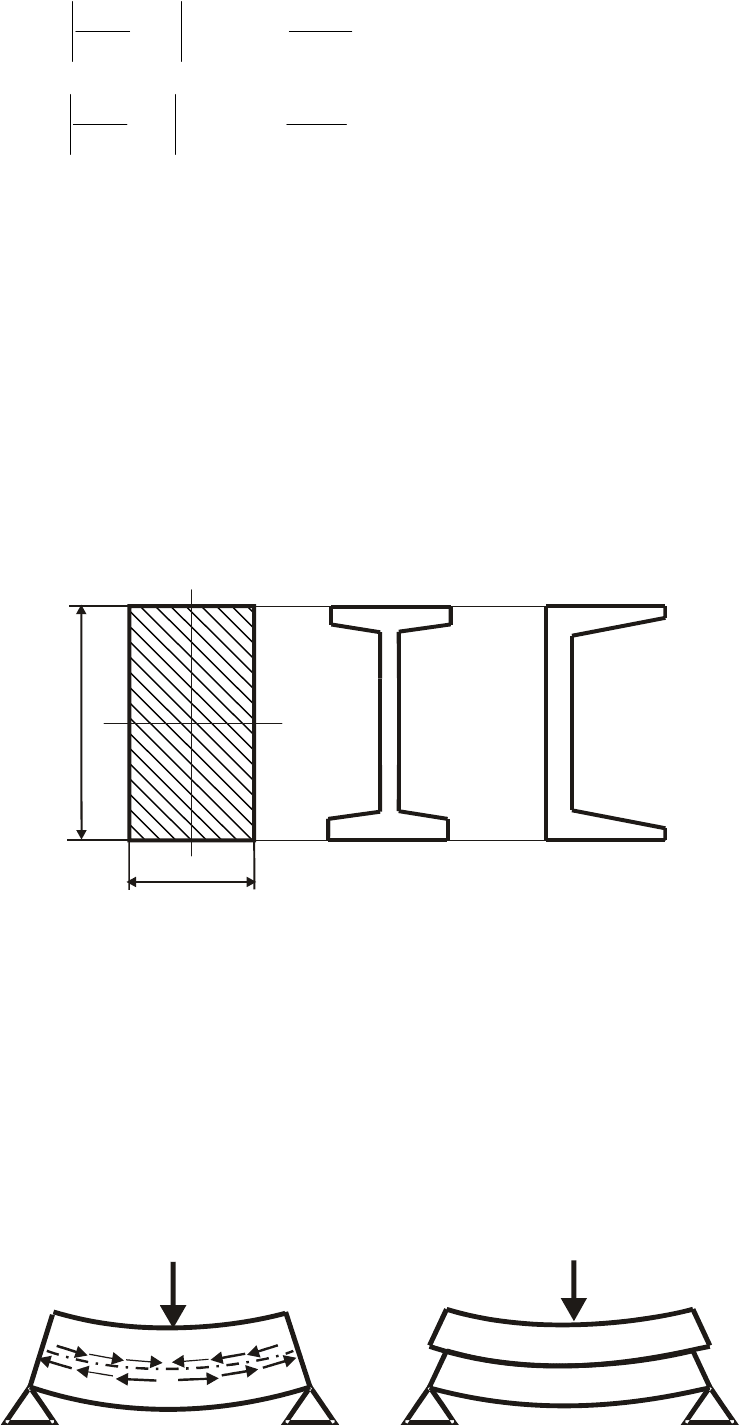
С точки зрения экономии металла рационально вырезать часть металла вблизи
нейтральной оси (рис. 7.5). Так прямоугольное сечение целесообразно заменить
двутавровым. При этом момент сопротивления сечения балки уменьшается
незначительно. а площадь уменьшается в несколько раз. Таким образом при тех
же нагрузках вес балки резко уменьшается.
z
W
A
Тот же эффект получается при замене прямоугольного сечения швеллером, но в этом
случае возможно скручивание балки, о чем будет сказано в следующем разделе.
Существенной экономии материала можно достигнуть также при замене
прямоугольного сечения коробчатым (для деревянных балок) или кольцевым
(балка — труба).
h
b
двутавр швеллер
Рис. 7.5. Рациональные формы сечения балки
7.2 Касательные напряжения при изгибе
При поперечном изгибе в сечениях балки действуют два внутренних усилия:
изгибающий момент, вызывающий появление нормальных напряжений
σ
и
поперечная сила, вызывающая появление касательных напряжений
τ
.
По закону парности касательных напряжений появление
τ
в поперечных сечениях
балки влечет за собой появление
τ
в продольных сечениях (вдоль волокон).
Рассмотрим две балки: одну сплошную (рис.7.6, а) и другую, составленную из двух
отдельных листов (рис. 7.6, б). Под действием поперечной нагрузки балки
изгибаются. В балке, составленной из листов, хорошо видны сдвиги между листами.
В сплошной балке таких сдвигов нет. Возникающие между слоями касательные
напряжения компенсируют сдвиги, сохраняя неразрывность балки.
F
F
t
t
)
a
)
б
Рис. 7.6. Касательные напряжения при изгибе балки
67
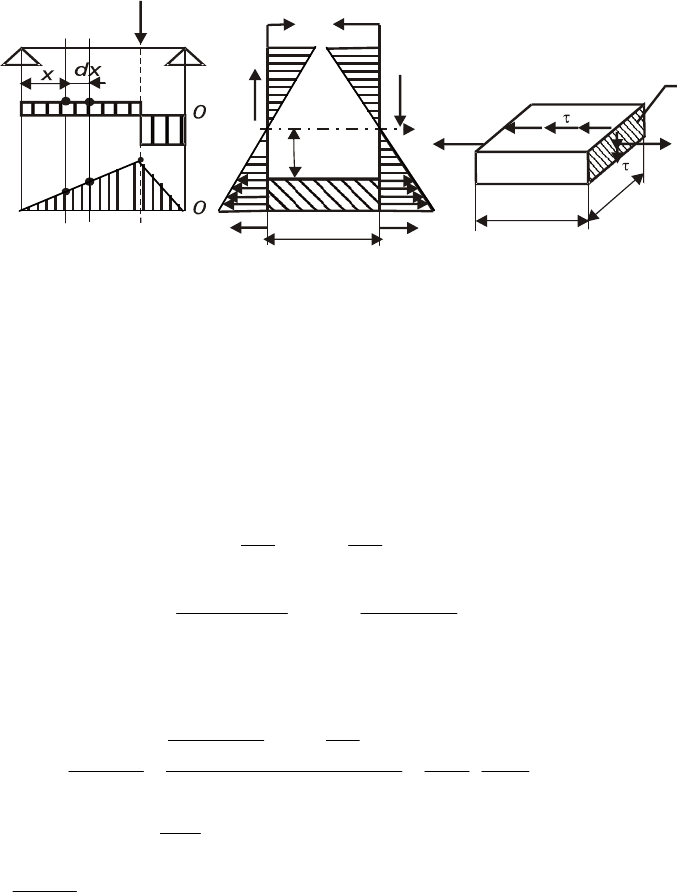
Распределение
τ
по ширине сечения балки неизвестно, поэтому для решения
поставленной задачи примем две гипотезы:
Касательные напряжения по ширине сечения распределены равномерно,
В поперечном сечении касательные напряжения параллельны линии действия
поперечной силы.
В действительности эти гипотезы справедливы лищь для прямоугольного
поперечного сечения. Однако выведенную с использованием этих гипотез формулу
используют и для некоторых других форм поперечного сечения.
Для вывода формулы касательных напряжений
τ
для балки, нагруженной силой
F
,
построим эпюры изгибающих моментов
z
M
и поперечных сил (рис. 7.7). Q
dx
y
x
N
2
dx
b
1
σ
2
σ
N
1
F
Q
Q
Q
zz
M
dM
+
zz
MdM+
z
M
z
M
z
M
отс
A
Рис. 7.7. К выводу формулы касательных напряжений при изгибе балки
Вырежем из сплошной балки элемент длиной . Внутренние усилия с левой и с
правой сторон элемента различны. Слева действуют
dx
z
M
и , справа Q
zz
M
dM+
и .
Q
От выбранного элемента на некотором расстоянии от нейтральной оси
продольным сечением отрежем нижнюю часть и рассмотрим ее равновесие.
y
12
0
x
FN bdxN
τ
=− − ⋅ ⋅ + =
∑
,
где
отс отс
отс
11
=⋅= ⋅=
∫∫
zz
z
zz
A А
MM
N
dA y dA S
JJ
σ
,
отс отс
отс
22
()
zz zz
z
zz
AA
MdM MdM
N
dA y dA S
JJ
σ
++
=⋅= ⋅=
∫∫
,
отс
отс
z
A
Sy=⋅
∫
dA.
Тогда
отс отс
отс
1
bdx
zz z
zz
zzz
z
MdM M
SS
NJ J dMS
bdx dx bJ
τ
2
+
−
Ν−
== =⋅
⋅⋅
z
⋅
.
С учетом
z
dM
Q
dx
=
отс
z
z
QS
b
J
⋅
τ=
⋅
(7.9).
Полученная формула (7.9) носит название — формула Журавского.
В этой формуле:
Q — поперечная сила в сечении,
— ширина сечения на том уровне, где определяются касатедьные
напряжения,
b
z
J
— момент инерции всего сечения относительно нейтральной оси,
— статический момент относительно нейтральной оси части сечения,
расположенной выше или ниже уровня, где определяются касательные
напряжения.
отс
z
S
7.2.1. Распределение касательных напряжений в сечениях
различной формы
Рассмотрим распределение касательных напряжений в сечениях различной формы.
68

Прямоугольное сечение
Дано: , , (рис. 7.8)
Q b h
h
y
c
отс
Z
y
в
А
отс
max
τ
Рис. 7.8. Касательные напряжения в прямоугольном сечении балки при изгибе
3
12
z
bh
J
⋅
=
2
отс отс отс 2
1
22 2 24
zc
hhbh
SAy b y y y
⎛⎞
⎛⎞⎛⎞
=⋅=⋅−⋅+=⋅−
⎜
⎜⎟⎜⎟
⎜
⎝⎠⎝⎠
⎝⎠
⎟
⎟
(7.10),
где
отс
2
h
Ab y
⎛
=⋅ −
⎜
⎝⎠
⎞
⎟
— площадь отсеченной части сечения,
отс
1
22
c
h
y
⎛
=+
⎜
⎝⎠
y
⎞
⎟
— расстояние от центра тяжести отсеченной части до нейтральной
оси.
Выражение (7.10) представляет собой уравнение параболы. На поверхности балки
при
2
h
y =±
=
отс
0
z
S
τ
=0. На нейтральной оси при 0y
=
отс
z
S достигает
максимума.
max
3
33
24
22
12
hh
Qb
QQ
bh A
bh
b
ττ
⋅⋅ ⋅
== =⋅=⋅
⋅
⋅
⋅
Круглое и кольцевое сечения
Дано: , .
Q d
Для круглого поперечного сечения несправедлива гипотеза о том, что касательные
напряжения
τ
параллельны поперечной силе Q (рис.7.9).
Z
y
d
d
D
max
τ
max
τ
69

Рис. 7.9. Касательные напряжения в круглом сечении балки при изгибе
Закон распределения
τ
не может быть определен по формуле Журавского. Однако
на уровне нейтральной оси , где все
τ
параллельны поперечной силе , можно по
формуле Журавского определить максимальные касательные напряжения
Q
(
)
отс
max
max
z
z
QS
bJ
τ
⋅
=
⋅
.
В этом выражении
bd=
4
64
z
d
J
π
=
23
отс
2
83 12
z
ddd
S
π
π
=⋅=
Тогда
3
max
4
64 4
3
12
Qd Q
A
dd
τ
π
⋅⋅
==
⋅⋅
⋅
.
Для кольцевого сечения, применяя формулу Журавского также можно найти
max
τ
на
уровне нейтральной оси, рассматривая кольцо как разность двух кругов. В
зависимости от толщины кольца
max
4
2
3
QQ
AA
τ
<<.
Для тонкостенных колец можно принять
max
2
Q
A
τ
≈ .
Двутавровое сечение
Двутавр приближенно можно рассматривать как сечение, состоящее из трех
прямоугольников (рис. 7.10). В прямоугольном сечении касательные напряжения
распределены по параболе.
τ
На поверхности
τ
=0. На нейтральной оси
max
τ
τ
=
. В месте перехода от полки к
стенке двутавра его ширина уменьшается примерно в 15 раз. Соответственно во
столько же раз скачкообразно увеличиваются касательные напряжения.
b
z
y
z
τ
y
τ
max
τ
x
y
τ
xz
τ
Рис. 7.10. Касательные напряжения в двутавровой балке при изгибе
Следует отметить, что в полках двутавра, кроме вертикальных касательных
напряжений
y
τ
действуют еще и горизонтальные
z
τ
, направленные, как показано на
рис. 7.10. Они образуют поток касательных напряжений, который для двутавра
является самоуравновешенным.
Швеллер
В швеллере касательные напряжения образуют неуравновешенный поток, который
может вызвать скручивание балки (рис. 7.11, а). Чтобы компенсировать
скручивающее действие касательных напряжений внешнюю силу рекомендуется
прикладывать не в центре тяжести швеллера, а сместить так, чтобы момент силы
относительно продольной оси уравновешивал поток касательных напряжений
(рис. 7.11, б).
Точка, в которую надо сместить силу, чтобы она уравновешивала скручивающее
действие потока касательных напряжений, называется центром изгиба
.
70
