Макаров Е.Г. Сопротивление материалов
Подождите немного. Документ загружается.


2
упр т т
6
bh
MW
σσ
== .
При дальнейшем увеличении нагрузки у поверхности балки появляется пластическая
зона
, которая увеличивается с ростом нагрузки. В центре балки сохраняется упругая
зона (рис
. 8.2).
При дальнейшем увеличении нагрузки зона упругопластической деформации растет
,
постепенно захватывая почти все сечение
.
Рассмотрим идеальный случай
, когда все сечение пластически деформируется.
Напряжения во всех точках сечения равны пределу текучести
. Такое предельное
состояние называется
пластический шарнир
.
При постоянной нагрузке части балки
слева и справа от сечения взаимно разворачиваются (балка представляет собой
пластический механизм)
. Практически при любых максимальных деформациях на
нейтральной оси деформация равна нулю и в центре сечения остается, пусть и
маленькая, упругая зона.
Найдем предельный изгибающий момент
, возникающий в пластическом шарнире.
Из условия эквивалентности напряжений и внутренних усилий (1
.3).
А
M
ydA
σ
=⋅⋅
∫
.
При изгибе напряжения в верхних и нижних волокнах балки имеют различный знак
.
Однако в функциях аппроксимации диаграммы напряжения не меняют знак
автоматически при перемене знака координаты
y
. Как следствие этого в
пластическом шарнире .
0=⋅⋅=
∫
Т
А
MydA
σ
Для возвращения к здравому смыслу возьмем сумму интегралов для сжатой и
растянутой частей сечения
раст сжат
пласт т т
АА
M
ydA ydA
σσ
=⋅⋅+⋅⋅
∫∫
.
С учетом выражение для предельно возможного изгибающего момента в
прямоугольном поперечном сечении примет вид
dA b dy=⋅
2
2
пласт т т
0
2
4
h
bh
Mybdy
σσ
=⋅⋅⋅=
∫
.
В условиях пластической деформации балка может выдержать в полтора раза
большую нагрузку
, чем при упругой деформации
пласт
упр
1, 5
M
M
= .
Найдем изгибающий момент при упругопластическом изгибе
упр-пласт
А
M
ydA
σ
=⋅⋅
∫
. (8.1).
Напряжения
σ по высоте сечения переменные.
E
σ
ε
=⋅, если деформация упругая
т
ε
ε
<
,
σ
ε
=Φ( ), если деформация упругопластическая
т
ε
ε
≥ . (8.2)
Здесь
ε
Φ( ) — уравнение диаграммы деформирования, зависящее от принятой
аппроксимации диаграммы
.
Mathcad позволяет записать зависимость
σ
от координаты выбранной точки в
виде одной функции с помощью условного оператора (см. примеры в электронной
книге
y
Для главы 8). Для этого надо знать координату границы упругой и
упругопластической зон
.
т
y
На эпюре деформаций
ε
(рис. 8.2) рассмотрим три подобных треугольника.Запишем
отношение их катетов
max
т
т
2hyy
ε
ε
ε
==.
Из этого выражения находим величины
ε
и в зависимости от
т
y
max
ε
.
т
т
max
2
h
y
ε
ε
=
max
2
y
h
ε
ε
= (8.3).
Здесь
тт
E
ε
σ
= — деформация, соответствующая пределу текучести.
Решить упругопластическую задачу легче, задаваясь деформацией, а не нагрузкой
.
Порядок расчета
Задаемся
max
ε
. По выражениям (8.3), затем (8.2) и (8.1) определяем изгибающий
момент
. Cтроим график
упр-пласт
M
M
от
ε
и уже по графику для заданного
81
момента определяем, соответствующую ему деформацию
max
ε
. Для найденного
значения
max
ε
находим зависимость
σ
от . y
8.3.1. Остаточные напряжения при упругопластической
деформации при изгибе
В пластически деформированной балке при разгрузке возникают остаточные
напряжения
. Определим величину остаточных напряжений.
При определении остаточных напряжений следует учесть
, что при нагрузке
распределение напряжений упругопластическое
,
при разгрузке — чисто упругое.
Пусть балку нагрузили моментом
. После разгрузки
нагр
M 0M
=
. Состояние
разгрузки можно представить как сумму моментов нагрузки и разгрузки
, равную
нулю
нагр разгр
0MM
+
= . Откуда
нагр пласт разгр max .разгр
A
M
ydA M W
σσ
−=− ⋅= =
∫
(8.4),
где
W — момент сопротивления сечения. Для прямоугольного сечения
2
6
bh
W
⋅
=
.
Из выражения (8
.4) находим максимальное упругое напряжение при разгрузке
. По высоте сечения упругие напряжения распределены по линейному
закону
. Тогда из подобия треугольников
max,разгр
σ
max.разгр
разгр
2
y
h
σ
σ= .
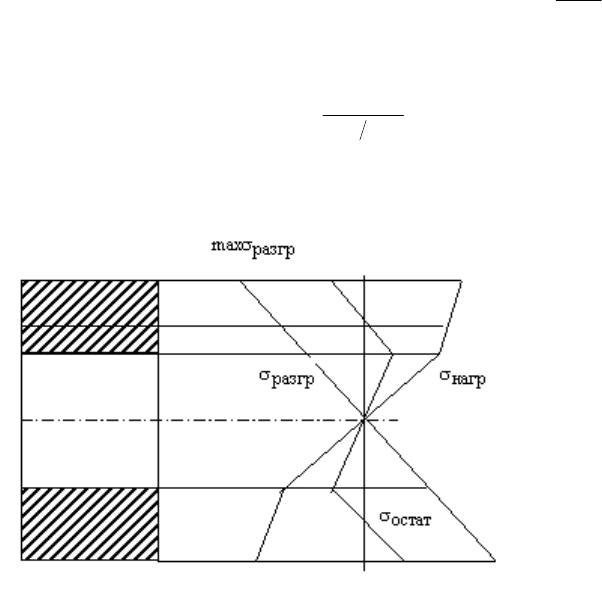
Остаточные напряжения определяются как сумма напряжений нагрузки и разгрузки
(рис. 8.3).
ост нагр разгр
σ
σσ
=+ .
Рис. 8.3 Определение остаточных напряжение при упругопластическом изгибе балки
Пример расчета напряжений при изгибе балки с учетом пластических деформаций
приведен в электронной книге в разделе
Для главы 8.
8.4 Учет пластических деформаций при
кручении
При кручении крутящий момент определяется методом сечений, как указано в
главе 2
, независимо от величины деформации. а вот характер распределения
напряжений в поперечных сечениях стержня оказывается различным при упругих и
упругопластических деформациях
.
Как и при изгибе для облегчения расчетов примем дополнительную гипотезу
,
аналогичную гипотезе плоских сечений
.
ГИПОТЕЗА
При кручении, прямолинейные радиусы остаются прямыми как при упругих, так и
упругопластических деформациях балки.
На основании этой гипотезы можно считать, что при кручении деформации в
круглом поперечном сечении распределены по линейному закону
, как при упругой,
так и при упругопластической деформации (рис
. 8.4).
82

d
0
r
Т
r
пластический
шарнир
max
т
τ
т
τ
т
γ
max
τ
Упругая
зона
Пластическая
зона
Рис. 8.4. Распределение деформаций и напряжений при упругопластическом кручении
стержня
Для определения напряжений при упругопластической деформации надо построить
диаграмму деформирования в координатах
γ
τ
−
и по этой диаграмме для заданного
значения деформации
γ
определить, соответствующее ей значение напряжения .
Величина напряжения
τ
τ
будет зависеть от выбранного вида аппроксимации
диаграммы деформирования
.
Будем постепенно увеличивать нагрузку на стержень и соответственно крутящий
момент.
Деформации и напряжения в сечении распределены по линейному закону до тех пор
,
пока на поверхности стержня напряжения не достигнут предела текучести
max т
τ
τ
= .
Найдем предельный крутящий момент при упругой деформации
3
к.упр т т
16
p
d
MW
π
ττ
== .
При дальнейшем увеличении нагрузки у поверхности стержня появляется
пластическая зона
, которая увеличивается с ростом нагрузки. В центре стержня
сохраняется упругая зона (рис
. 8.4).
При дальнейшем увеличении нагрузки зона упругопластической деформации растет
,
постепенно захватывая почти все сечение
.
Рассмотрим идеальный случай
, когда все сечение пластически деформируется.
Напряжения во всех точках сечения равны пределу текучести
. Как и при изгибе,
такое предельное состояние называется
пластический шарнир
.
Пластическим щарниром считается состояние, при котором крутящий момент
практически не растет и деформация происходит при постоянной нагрузке
.
При постоянной нагрузке части стержня слева и справа от сечения взаимно
разворачиваются (стержень превратился в пластический механизм)
.
Понятие пластический шарнир имеет смысл только при использовании диаграммы
Прандтля
.
Справедливости ради надо отметить
, что и при использовании диаграммы Прандтля
крутящий момент
, хоть и очень медленно, но растет за счет уменьшения упругого
ядра в центре сечения стержня
.
Найдем предельный крутящий момент
, возникающий в пластическом шарнире.
Из условия эквивалентности напряжений и внутренних усилий (1
.3).
к
А
M
rdA
τ
=⋅⋅
∫
.
С учетом
2dA r dr
π
=⋅ выражение для крутящего момента в круглом поперечном
сечении примет вид
3
2
к.пласт т т
2
12
d
d
Mrdr
π
πτ τ
2
0
=⋅=
∫
.
В условиях пластической деформации стержень может выдержать значительно
большую нагрузку
, чем при упругой деформации
к.пласт
к.упр
1, 33
M
M
=
.
Найдем крутящий момент при упругопластическом кручении
к.пласт
А
M
rdA
τ
=⋅⋅
∫
. (8.5).
Напряжения по высоте сечения переменные
. τ
G
τ
γ
=⋅, если деформация упругая
т
γ
γ
<
,
τ
γ
=Φ( ), если деформация упругопластическая
т
γ
γ
≥ . (8.6)
83
Здесь
γ
Φ( ) — уравнение диаграммы деформирования при кручении, зависящее от
принятой аппроксимации диаграммы
.
Mathcad позволяет записать зависимость
τ
от координаты выбранной точки в
виде одной функции с помощью панели программирования. Для этого надо знать
координату границы упругой и упругопластической зон
.
r
т
r
На эпюре деформаций
γ
(рис. 8.4) рассмотрим три подобных треугольника.
Запишем отношение их катетов
.
max
т
т
2rdr
γ
γ
γ
== .
Из этого выражения находим величины
γ
и в зависимости от
т
r
max
γ
т
т
max
2
d
r
γ
γ
=
max
2
r
d
γ
γ
= (8.7).
Здесь
тт
G
γ
τ
= — деформация, соответствующая пределу текучести.
Выберем переменную для расчета
. Как и при изгибе, можно задаваться величиной
деформации
max
γ
и по ней находить распределение напряжений по сечению стержня
и соответствующий ей крутящий момент
, но при кручении удобнее задаваться углом
поворота сечения
. φ
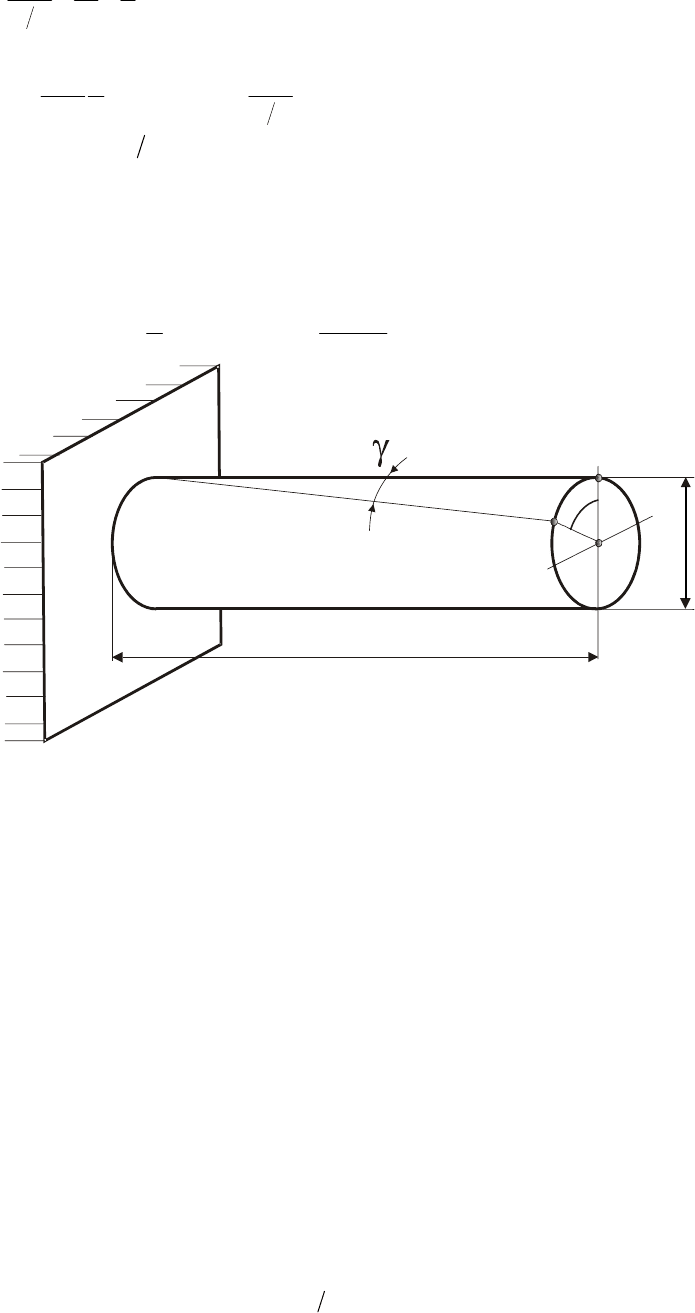
Запишем связь между углами
φ
и
γ
. Как видно из рисунка 8.5
1max
2
d
AA L
γ
φ
=⋅=⋅ откуда
max
2 L
d
γ
φ
= . (8.8).
А
А
1
L
d
ϕ
Рис. 8.5. Связь между углом закручивания
ϕ
и углом сдвига
γ
Порядок расчета: Задаемся
ϕ
. По выражениям (8.8), затем (8.7), (8.6) и (8.5)
определяем изгибающий момент
.
к.упр-пласт
M
Cтроим график зависимости
к
M
от
ϕ
и уже по графику для заданного момента
определяем
, соответствующий ему угол закручивания
ϕ
.
Для найденного значения
ϕ находим зависимость
τ
от . r
Пример расчета напряжений при кручении стержня с учетом пластических
деформаций приведен в электронной книге в разделе
Для главы 8.
8.5 Расчеты по предельной нагрузке
Рассмотрим приближенные методы оценки допускаемой нагрузки на
рассматриваемую конструкцию
.
Во всех предыдущих разделах в качестве условия выхода конструкции из строя
принималось
max пред
σ
σ
= . Где в качестве
пред
σ
принимался предел прочности для
материалов в хрупком состоянии или предел текучести для материалов в пластичном
состоянии
.
Другими словами
, конструкция из пластичного материала выходит из строя, если в
самой нагруженной точке напряжение достигает предела текучести
. А условие
прочности имеет вид
[
]
max т
n≤σσ=σ, где n —коэффициент запаса.
Такой расчет носит название
расчет по допускаемым напряжениям
.
Однако, как видно из предыдущих параграфов этой главы, появление пластических
деформаций в конструкции еще не означает выход конструкции из строя
.
Конструкция из пластичных материалов вполне может воспринимать нагрузку
,
гораздо большую
, чем найденная расчетом по допускаемым напряжениям.
84
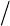
Был предложен другой метод расчета, названный расчетом по несущей способности
или расчетом по допускаемым нагрузкам
.
За выход из строя в этом методе принимается перемещение конструкции или части ее
при постоянной нагрузке
, то есть превращение системы в пластический механизм
при появлении в ней пластических шарниров
.
При этом условие выхода из строя .
пред
PP=
Условие прочности
[
]
пред
PPP n≤= , где — нагрузка, при которой система
превращается в пластический механизм
.
пред
P
В расчетах по допускаемым нагрузкам используется схематизированная диаграмма
деформирования идеального жесткопластического тела (рис. 8.1, а)
, представляющая
собой одну горизонтальную линию
т
σ
=σ (без учета упругих деформаций).
При деформация
, то есть материал считается абсолютно жестким
(недеформируемым)
. При деформация
т
σ<σ ε=0
т
σ=σ
ε
→∞.
Возможны два состояния конструкции при использовании такой диаграммы
:
пластический шарнир уже есть, но система еще не механизм — это статически
возможное состояние
.
В статически возможном состоянии выполняются уравнения равновесия.
система уже превратилась в пластический механизм — это кинематически
возможное состояние
.
В кинематически возможном состоянии выполняются уравнения неразрывности
деформаций
, так как разрушения конструкции не происходит.
В теории пластичности доказываются статическая и кинематическая теоремы [5],
[15]
. Приведем их формулировки без доказательств.
Статическая теорема.
Нагрузка, соответствующая статически возможному состоянию всегда меньше
предельной нагрузки
. Эта теорема — основа статического метода расчета (метода
нижней оценки)
.
Кинематическая теорема.
Нагрузка
, соответствующая кинематически возможному состоянию всегда больше
предельной нагрузки
. Эта теорема — основа кинематического метода (метода
верхней оценки)
.
Для определения предельной нагрузки расматриваются различные возможные
состояния и определяется нагрузка для каждого из них
Наибольшая из всех статически возможных нагрузок ближе всего к предельной
(метод нижней оценки)
.
В методе нижней оценки величина предельной нагрузки определяется из условий
равновесия системы
.
Наименьшая из всех кинематически возможных нагрузок ближе всего к предельной
(метод верхней оценки).
В методе верхней оценки величина предельной нагрузки определяется из условия
равенства работ внешних и внутренних сил при перемещении системы
.
Рассмотрим примеры определения предельной нагрузки
.
Пример 1
Рассмотрим балку
, защемленную двумя концами, нагруженную силой
F
(рис. 8.6, а).
В упругой постановке такая балка 2 раза статически неопределима
. Решение такой
задачи методом сил будет рассмотрено в главе 11
.
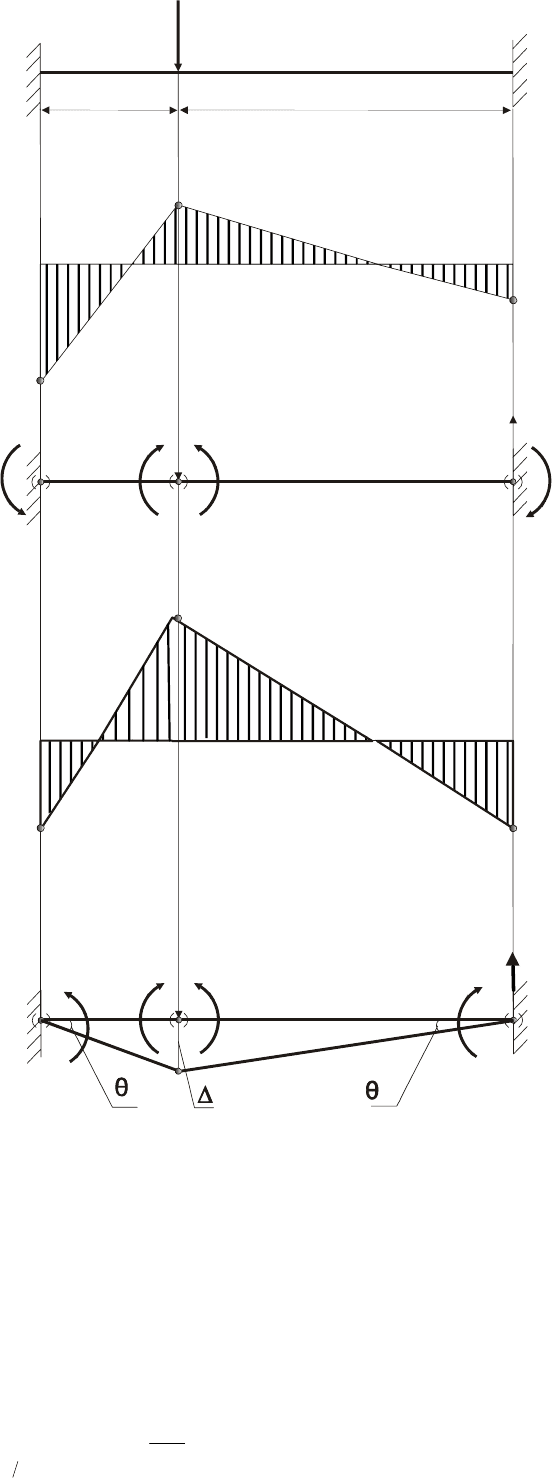
На рис. 8
.6, б приведена эпюра изгибающих моментов в сечениях балки, найденная
методом сил при упругой деформации (при
2ca
=
). Однако предельную нагрузку на
балку можно оценить методами верхней и нижней оценки (наличия упругого
решения не требуется)
.
Метод нижней оценки (статический метод)
При постепенном увеличении нагрузки пластические шарниры образуются сначала в
сечении D
, затем в сечении В, затем в сечении А. Это три статически возможных
состояния (с одним, двумя и тремя шарнирами). Предельным является состояние
,
когда в балке образуются 3 пластических шарнира
. После этого система
превращается в пластический механизм
.
Рассматриваем предельное состояние
, когда шарниры уже есть, но система еще не
превратилась в пластический механизм
. Схема нагружения балки в предельном
состоянии (с тремя шарнирами) показана на рис
. 8.6, в, эпюра изгибающих моментов
в предельном состоянии — на рис
. 8.6, г.
85
D
А
B
F
ас
0,296 F
a
-0,444 F
a
-0,222 F
a
а)
б)
D
А
B
F
пред
в)
М
пл
М
пл
М
пл
М
пл
R
a
М
пл
-М
пл
-М
пл
D
АB
F
пред
д)
М
пл
М
пл
М
пл
М
пл
R
a
D
А
г)
Рис. 8.6. Образование пластических шарниров в балке
В пластическом шарнире в каждой точке сечения
т
σ
σ
=
. Тогда изгибающий
момент в пластическом шарнире
пл т
0
A
MydA
σ
=⋅=
∫
, так как в этом выражении не учтен знак напряжения (плюс в
растянутых волокнах и минус в сжатых)
. Запишем изгибающий момент как сумму
моментов от напряжений в растянутых и сжатых волокнах
.
раст сжат
пл т т
AA
M
ydA ydA
σσ
=⋅+⋅
∫∫
.
Для балки прямоугольного сечения это выражение примет вид
2
пл т т
2
2
4
A
bh
M
ydA Const
σσ
=⋅==
∫
.
Запишем условия равновесия балки в шарнирах
А
,
В и D.
(1)
плA
M
M=− ,
(2)
пл плBA
M
MRcM=− + ⋅ = ,
(3)
пл пред пл
()
DA
M
MRacFaM=− + + − =− .
86

Из выражения (3)
предA
a
RF
ac
=
+
.
Из выражения (2)
пл пред
2
A
ac
MRcF
ac
⋅
=⋅=
+
,
пред пл
2
ac
FM
ac
+
=
⋅
.
При
2ca=
2
пл
пред пл т
23
23
2a44
M
aa bh
FM
aa
σ
+
===
⋅
(8.10).
Метод верхней оценки (кинематический метод)
Есть три пластических шарнира. Система уже пластический механизм. Происходит
перемещение при постоянной нагрузке (предельной)
. Шарнир В перемещается при
постоянной нагрузке
, его перемещение
Δ
в некоторый момент времени (рис. 8.6, д)
Работа внешних сил (силы
F
)
внеш
=⋅ΔAF.
Участки АВ и ВD прямолинейные, так как используется диаграмма
жесткопластического тела и при
т
σ
σ
<
деформаций нет. Участок АВ
поворачивается на угол
A
θ
, участок ВD поворачивается на угол
θ
D
.
Работа внутренних сил складывается из работ моментов в пластических шарнирах
А
, В, D. В среднем шарнире В взаимный угол поворота двух частей балки равен
сумме углов
A
θ
и
D
θ
.
внутр
пл пл пл
()=++ +
A
DA
AMMM
D
θ
θθθ
.
Найдем связь между углами
A
θ
и
D
θ
()
A
tg
c
θ
Δ
=
()
D
tg
a
θ
Δ
=
. Углы малы, так как рассматривается начальный момент
образования пластического механизма, и
()
tg
θ
≈θ.
тогда
A
D
ca
θ
θ
Δ= ⋅ = ⋅ , откуда
DA
c
a
θθ
= .
Приравняв работу внешних и внутренних сил
, находим предельную силу
пред пл
22
AAA
c
Fc M
a
θθθ
⎛⎞
⎛⎞
⋅= +
⎜⎟
⎜⎟
⎝⎠
⎝⎠
.
Откуда
пред пл
2FM
ac
⎛⎞
=
⎜⎟
⋅
⎝⎠
ac+
.
При
2ca=
2
пл
пред т
3
3
a4
M
bh
F
a
σ
== .
Значения предельной нагрузки
, найденные кинематическим и статическим
методами (верхней и нижней оценки) совпали
, следовательно решение верное и
полное
.
пред
F
Если решения не совпадают
, следовательно рассмотрены не все возможные
состояния системы и правильное решение находится как раз среди нерассмотренных
состояний
.
Следует отметить
, что определение предельной нагрузки кинематическим методом
(верхней оценки)
, как правило, значительно проще, чем статическим методом
(нижней оценки)
.
Рассмотрим еще один пример
, где для определения предельной нагрузки надо
рассмотреть несколько возможных состояний
.
Пример 2
Рассмотрим раму
, нагруженную двумя силами (рис. 8. 7, а). Определим предельную
нагрузку
F
кинематическим методом (верхней оценки).
87

1
2
3
4
5
F
2F
L
1,5L
1
2
3
4
5
L
1,5L
1
2
3
4
5
L
1,5L
1
2
3
4
5
L
1,5L
1
2
3
4
5
L
1,5L
М
пл
θ
М
пл
θ
М
пл
1
2
3
4
5
L
1,5L
М
пл
М
пл
М
пл
F
2F
М
пл
θ
θ
гор
Δ
1
2
3
4
5
L
1,5L
М
пл
М
пл
F
2F
М
пл
θ
θ
М
пл
2
θ
θ
гор
Δ
верт
Δ
а) б)
в)
г)
Рис. 8.7. Кинематически возможные состояния рамы
Обозначим места возможного образования пластических шарниров цифрами 1 – 5.
Есть несколько вариантов превращения системы в пластический механизм
.
Система превращается в механизм при образовании пластических шарниров в
сечениях 2
, 3, 4 (рис. 8. 7, б). При этом верхняя часть рамы начинает перемещаться
без увеличения нагрузки (балочный механизм)
.
Система превращается в механизм при образовании пластических шарниров в
сечениях 1
,2, 4, 5 (рис. 8.7, в). Рама складывается как параллелограмм (механизм
бокового смещения)
.
Система превращается в механизм при образовании пластических шарниров в
сечениях 1
, 3, 4, 5 (рис. 8. 7, г). Это комбинированный механизм из двух
предыдущих
.
Определим предельную нагрузку в каждом из трех указанных возможных состояний
системы
.
Балочный механизм
внеш пред верт пред внутр пл
22 4AF FlA M
θ
θ
=Δ= ⋅== .
пред пл
2
F
Ml= .
Вертикальная сила
2
F
совершает работу на вертикальном перемещении .
Горизонтальная сила
верт
Δ
F
работу не совершает.
В пластических шарнирах 2 и 4 момент
пл
M
совершает работу на угле поворота
сечения
θ
. В шарнире 3 на взаимном угле поворота двух частей рамы 2
θ
.
Механизм бокового смещения
внеш пред гор пред внутр пл
1, 5 4AF F lA M
θ
θ
=Δ= ⋅= = .
пред пл
2,67
F
Ml= .
Горизонтальная сила
F
совершает работу на горизонтальном перемещении .
Вертикальная сила
гор
Δ
2
F
работу не совершает.
В пластических шарнирах 1
, 2, 4, 5 момент
пл
M
совершает работу на угле поворота
сечения
θ
.
Комбинированный механизм
внеш верт гор пред пред внутр пл
221,5AF F FlF lAM6
θ
θθ
=⋅Δ+⋅Δ= ⋅+ ⋅ = = ⋅
пред пл
1, 71
F
Ml= .
Вертикальная сила
2
F
совершает работу на вертикальном перемещении .
Горизонтальная сила
верт
Δ
F
совершает работу на горизонтальном перемещении
гор
Δ
В пластических шарнирах 1 и 5 момент
пл
M
совершает работу на угле поворота
сечения
θ
. В шарнирах 3 и 4 на взаимном угле поворота двух частей рамы 2
θ
.
Для трех кинематически возможных состояний рамы найдено предельное значение
силы
F
. Наименьшее из них
пред пл
1, 71
F
Ml
=
ближе всего к действительному
предельному значению
.
88
По статическому методу (нижней оценки) решение задачи сводится к составлению
уравнений равновесия и решению системы этих уравнений для каждого статически
возможного состояния
. Такое решение значительно более сложное, чем
кинематический метод (верхней оценки)
, и здесь не рассматривается.
Пример 3
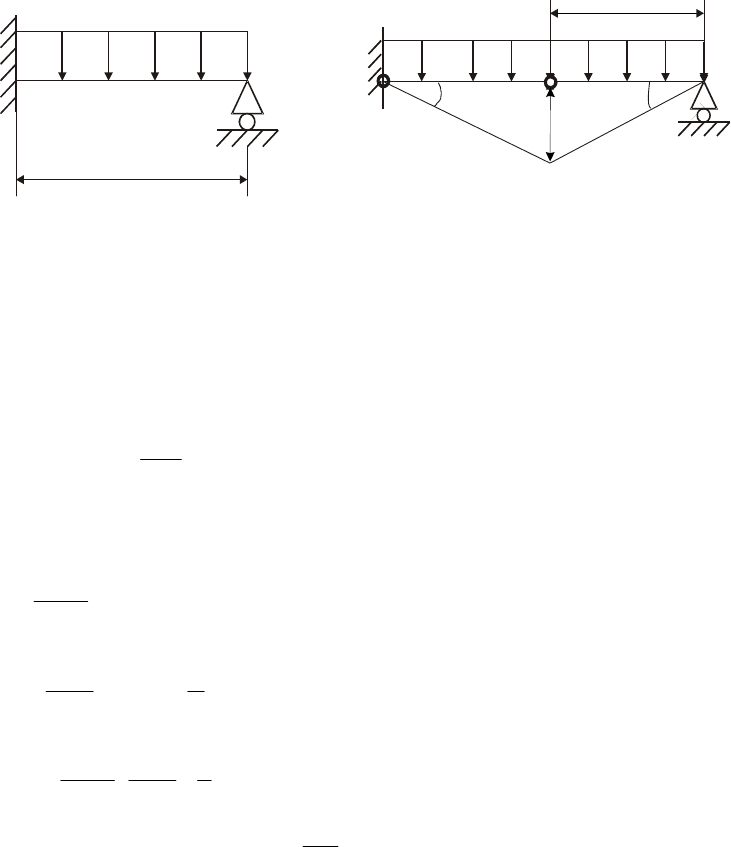
Статически неопределимая балка (рис. 8.8, а) нагружена распределенной нагрузкой.
Требуется определить предельную величину интенсивности распределенной
нагрузки. Найдем решение кинематическим методом (верхней оценки).
q
L
а) б)
q
пред
х
А
В
A
B
D
θ
θ
Δ
Рис. 8.8. Кинематически возможное состояние балки
Для различных кинематически возможных состояний переменными могут быть не
только число пластических шарниров, но и их положение.
В нашей задаче система превращается в пластический механизм при образовании
двух пластических шарниров: в точках А, и D (рис. 8.8, б). Положение шарнира D
может быть различным. Обозначим его положение координатой
x
. Найти положение
шарнира D, при котором предельная нагрузка на балку будет минимальной.
Подсчитаем работы внешних и внутренних сил.
внеш
2
Δ⋅
=Ω=
L
Aqq
, где — площадь, ограниченная положениями балки до и
после деформации.
Ω
(
)
внутр
пл
=++
A
AB
AM
θ
θθ
.
Из равенства работ внешних и внутренних сил найдем
()
пл
2
A
AB
M
q
L
θ
θθ
=++
Δ⋅
.
Величина углов
A
θ
и
B
θ
зависит от
x
A
Lx
θ
Δ
=
−
B
x
θ
Δ
=
.
С учетом выражений для углов выражение для нагрузки
q
пл
2
21
()
M
qx
LLxx
⎛⎞
=+
⎜⎟
−
⎝⎠
.
Для нашего примера
2
пл т
4
bh
M
σ
= — предельный пластический момент в
прямоугольном сечении балки.
Далее надо построить график зависимости q(x) по длине балки. Минимальное
значение q(x) на графике ближе всего к предельной нагрузке.
Решение этой задачи в Mathcad приведено в электронной книге в разделе
Для главы 8.
8.6. Понятие о приспособляемости конструкций
В этой главе говорилось о возможности и условиях возникновения пластических
деформаций в конструкциях при статическом однократном нагружении. Однако
практически любая конструкция испытывает многократное нагружение.
Так статически нагруженные здания и сооружения испытывают многократное
температурное нагружение (зима – лето, ночь – день). Для трубопроводов повторной
нагрузкой является периодическое изменение давления, для самолета — взлет –
посадка и так далее.
При многократном нагружении пластическая деформация приводит к сравнительно
быстрому разрушению конструкции.
Работа конструкций при повторных пластических деформациях недопустима.
В зависимости от условий эксплуатации возможны два варианта поведения
конструкции при повторных нагружениях [8].
Накопление пластических деформаций, ведущее к разрушению конструкции;
89
Приспособление конструкции, когда после одного или нескольких циклов
повторного нагружения пластические деформации исчезают и конструкция
испытывает чисто упругое нагружение.
Важнейшим фактором приспособляемости является наличие остаточных сжимающих
напряжений в опасных местах конструкции. Остаточные напряжения сжатия
складываются с рабочими растягивающими напряжениями. Их сумма должна
оставаться меньше предела текучести материала.
Создание остаточных напряжений сжатия широко используется в промышленности.
О технологических приемах создания остаточных напряжений сжатия говорится в
главе 17.
В главе 5 при рассмотрении диаграммы деформирования мягкой стали говорилось о
явлении наклепа. Нагружение образца выше предела текучести, разгрузка и
повторное нагружение приводят к повышению пределов пропорциональности и
текучести.
Предварительная пластическая деформация используется, в частности, для
увеличения рабочего диапазона нагрузок пружин (заневоливание пружин).
Опрессовка труб и сосудов давлением, вызывающим в них появление пластической
деформации, ведет к повышению допустимого рабочего давления.
Но не все так просто. Оптимальное давление опрессовки или нагрузка
предварительной пластической деформации требуют тщательного, чаще всего
экспериментального, определения оптимальной величины остаточных напряжений,
дающей наибольший эффект упрочнения.
Для приспособляемости конструкции необходимо, чтобы рабочая нагрузка была
меньше предельной, определяемой как описано в предыдущем разделе.
Есть и другие условия, ограничивающие приспособляемость конструкций, но они
выходят за рамки курса сопротивления материалов.
90
