Макаров Е.Г. Сопротивление материалов
Подождите немного. Документ загружается.


D
центр
изгиба
С
F
F
)б)а
)в
Рис. 7.11. Поток касательных напряжений в швеллере при изгибе
Теоретически положение центра изгиба определяется в теории расчета тонкостенных
стержней открытого профиля. На практике не рекомендуется использовать один
швеллер. Желательно, чтобы сечение балки было симметричным и, если нужно
использовать швеллер, сделайте симметричное сечение из двух швеллеров
(рис. 7.11, в).
7.2.2. Проверка прочности по касательным напряжениям
Для длинных балок максимальные касательные напряжения, как правило,
значительно меньше максимальных нормальных напряжений. Так для балки круглого
поперечного сечения, размеры которого подобраны из условия прочности по
нормальным напряжениям, при
max
100
σ
=
Мпа величина
max
2
τ
≈
МПа, то есть
пренебрежимо мала.
Необходимо также учесть, что нормальные напряжения максимальны на поверхности
балки и равны нулю на уровне нейтральной оси, а касательные напряжения равны
нулю на поверхности и максимальны на уровне нейтральной оси. Нет точки, в
которой одновременно действовали бы максимальные нормальные и максимальные
касательные напряжения.
Как правило, проверка прочности балки по касательным напряжениям не
производится. Однако в некоторых случаях все-таки приходится делать такую
проверку.
Проверка прочности балки по касательным напряжениям производится в следующих
случаях:
Для коротких балок,
Если силы приложены вблизи опор балки
Объяснение для обоих случаев одно. Рассмотрим две балки (рис. 7.12). Одна
нагружена силой
F
посередине (рис. 7.12, а), другая двумя силами 2
F
,
приложенными на сравнительно малом расстоянии от опор (рис. 7.12, б).
Для первой балки значительно больше, чем для второй.
Максимальная поперечная сила для обеих балок одинакова. Размеры
поперечного сечения подбираются по условию прочности
a
max
M
max
Q
[]
max
max
z
M
W
σ
σ
=≤.
2Р
Р
-Р
Q
M
d
1
Р
Р
-Р
Q
M
d
2
Р
а)
б)
12
dd
>
12
QQ
=
12
MM
>
max1 max 2
ττ<
Рис. 7.12. Зависимость внутренних усилий от положения сил на балке
Следовательно для первой балки размеры сечения будут больше. При
71
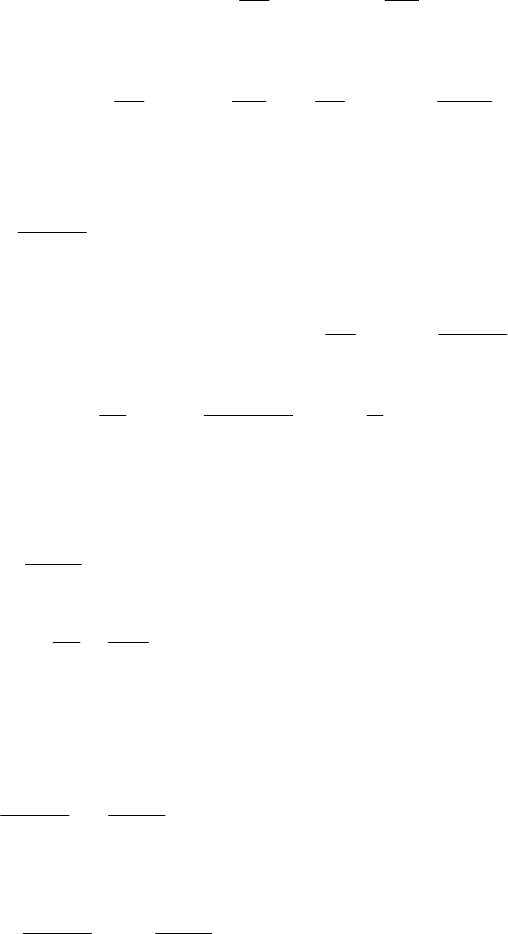
равенстве поперечных сил максимальные касательные напряжения будут
больше в балки меньшего поперечного сечения, то есть во второй (правой)
балке.
Если сечение имеет вырез вблизи нейтральной оси.
Например, для двутавровой балки или балки коробчатого сечения, так как,
согласно формуле Журавского, при уменьшении ширины поперечного
сечения в несколько раз во столько же раз увеличиваются касательные
напряжения и могут стать сопоставимы с нормальными напряжениями. Так
для двутавровой балки, если
max
100
σ
=
МПа, то
max
25
τ
≈
МПа.
Для материалов с пониженной сдвиговой жесткостью.
Например, для балок из пластмассы, дерева, композиционных материалов,
где волокна с высоким модулем сдвига скреплены между собой связующим
материалом с гораздо меньшим модулем сдвига.
7.3 Потенциальная энергия упругой деформации
при изгибе
Потенциальная энергия упругой деформации
П
при изгибе численно равна работе
внутренних сил, которая складывается из суммы работ (и соответственно суммы
потенциальных энергий) изгибающего момента
M
П
и поперечной силы
Q
П
=
M
Q
П
ПП+ .
Потенциальную энергию
M
П
, накопленную в теле, найдем как интеграл по объему
от удельной потенциальной энергии
0
П
, которая вызывается нормальными
напряжениями и равна
2
0
2
П
E
σ
= , где
z
z
M
y
J
σ
= , а элементарный объем
dV dA dx=⋅. Тогда
2
2
2
2
0
2
1
22
2
zz
M
z
VV lA lA
z
MM
П
П dV dV y dA dx y dA dx
EJE
JE
σ
σ
⎛⎞
⎛⎞
=== ⋅⋅=
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∫∫∫∫ ∫∫
где
2
z
A
ydA J
=
∫
. Окончательно получаем
2
2
z
M
z
l
M
dx
П
E
J
⋅
=
⋅
∫
.
Удельная потенциальная энергия от действия поперечной силы вызывается
касательными напряжениями и равна
Q
0
2
П
G
τ
τ
2
= , где
отс
z
z
QS
bJ
τ
⋅
=
⋅
. Тогда
(
)
2
2 отс
0
22
2
2
z
Q
z
VV lA
QS
A
ППdV dV dA dx
GA
bJ G
2
τ
τ
== = ⋅
∫∫ ∫∫
⋅
.
Для сохранения единообразия формул потенциальной энергии упругой деформации
выражение
Q
П
умножили и разделили на площадь поперечного сечения . Тогда
окончательно
A
2
2
Q
l
Qdx
П k
GA
=
⋅
∫
,
где
2
отс
2
z
A
z
SA
k
b
J
⎛⎞
=
⎜⎟
⎜⎟
⎝⎠
∫
dA
— коэффициент неравномерности распределения
касательных напряжений по сечению. Величина, в большинстве случаев, близкая к
единице .
11,2k =−
Выражение полной потенциальной энергии упругой деформации при изгибе имеет
вид
2
2
22
z
z
ll
Mdx
Qdx
П k
E
JG
⋅
=+
⋅⋅
∫∫
A
.
В случае наличия на балке нескольких участков с различной нагрузкой
подсчитывается сумма интегралов по количеству участков
2
2
22
z
z
ll
Mdx
Qdx
П k
E
JG
⋅
=+
⋅⋅
∑∑
∫∫
A
(7.11).
72
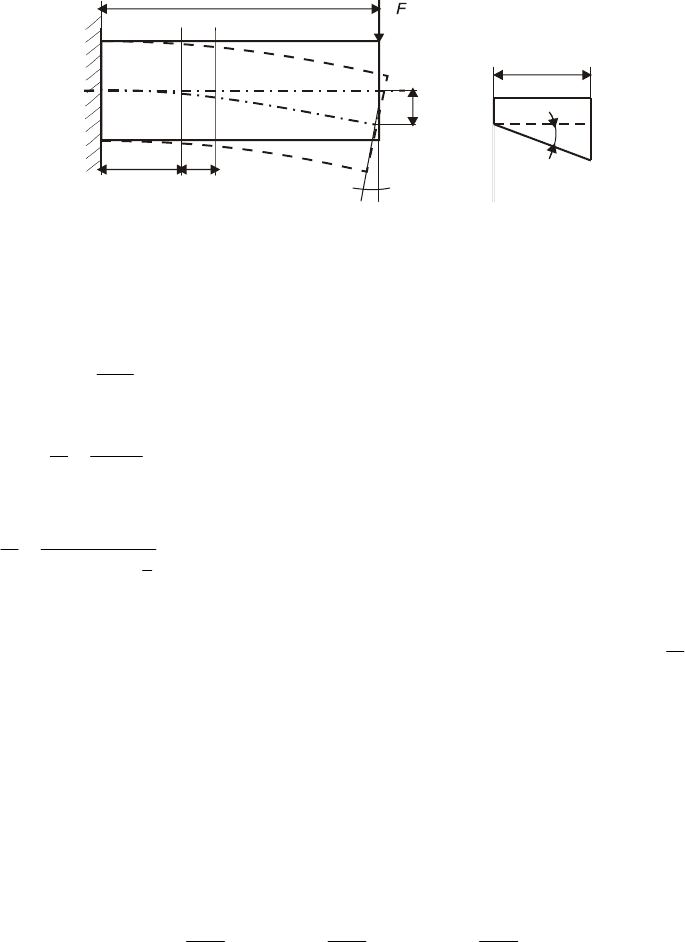
7.4 Перемещения при изгибе
Балка при изгибе искривляется. При этом каждое сечение получает два перемещения:
линейное — прогиб и угловое — угол поворота сечения (рис. 7.13).
Θ
L
u
L
L
dx
Θ
dx
x
u
y
u+du
yy
7.13. Перемещения балки при изгибе
Пусть в сечении
x
прогиб балки . В сечении
y
u
x
dx
+
прогиб балки .
Тогда ввиду малости перемещений по сравнению с длиной балки угол наклона
касательной к упругой линии балки
yy
udu+
tg( )=
y
du
dx
θθ
≈ (7.12),
Запишем уравнение упругой линии балки. По выражению (7.4) кривизна
балки
1
z
z
M
E
J
ρ
=
⋅
.
С другой стороны, из аналитической геометрии
()
3
2
2
1
1
y
y
u
u
ρ
′′
=
⎛⎞
′
+
⎜⎟
⎝⎠
.
Угол поворота сечения
0
y
u
θ
′
=≈
по сравнению с 1. Тогда кривизна балки
1
y
u
ρ
′′
≈
.
Приравнивая два выражения для кривизны балки получаем уравнение упругой линии
балки
zy z
E
Ju M
′′
= (7.13).
Для определения прогиба балки необходимо дважды проинтегрировать уравнение
упругой линии балки. Угол поворота сечения балки — это первая производная от
прогиба (7.12).
С учетом дифференциальных зависимостей между изгибающим моментом,
поперечной силой и интенсивностью распределенной нагрузки (3.12) можно
составить систему дифференциальных уравнений упругой линии балки
y
u
θ
′
=
z
y
z
M
u
E
J
′′
=
y
z
Q
u
E
J
′′′
=
IV
y
z
q
u
E
J
=
(7.14).
Перемещения при изгибе балок можно определить тремя способами:
1. Путем непосредственного интегрирования уравнения упругой линии балки;
2. Методом начальных параметров;
3. С помощью интеграла Мора.
7.4.1. Непосредственное интегрирование уравнения упругой
линии балки
Это самый простой способ определения перемещений балки при изгибе. Необходимо
составить уравнение изгибающего момента для заданной балки и, записав уравнение
(7.13), проинтегрировать его — получим уравнение углов поворота сечений балки.
После второго интегрирования получим уравнение прогибов балки.
zy z
E
Ju M
′′
=
zzyz
E
JEJuMdx
θ
′
== +
∫
C
zy z
E
Ju Mdxdx Cx D=+
∫∫
+.
Произвольные постоянные интегрирования определяются из граничных условий
закрепления балки. Если на балке участков с различной нагрузкой, для каждого
участка составляется свое уравнение упругой линии, дающее после интегрирования
две произвольные постоянные.
n
73
Всего — 2 постоянных, для определения которых надо составить систему из
уравнений и решить ее. Это создает большие трудности при определении
перемещений вручную с помощью микрокалькулятора.
n 2n
При использовании Mathcad таких трудностей нет. Уравнение изгибающего момента
единое для всех участков записывается с использованием операторов условия. А
встроенная функция
Odesolve легко решает любое дифференциальное уравнение.
7.4.2. Метод начальных параметров
Метод начальных параметров — это способ решения дифференциальных уравнений,
при котором неизвестными параметрами являются значение функции и ее
производных в начале координат. Для уравнения упругой линии — это будут прогиб
и угол поворота в начале координат на левом конце балки.
Для балки с несколькими участками, для того чтобы произвольные постоянные
интегрирования на всех участках были равны, надо, чтобы слагаемые уравнения
изгибающих моментов не менялись при переходе от одного участка к другому. Для
этого используются два приема:
Момент пары сил умножается на фиктивное плечо в нулевой степени
0
0
()
m
MMxa=−;
Распределенная нагрузка принимается действующей до конца балки. А
чтобы не нарушить условия нагружения, в сечении, где заканчивается
реальная нагрузка, прикладывается равная по величине распределенная
нагрузка противоположного направления, также действующая до конца
балки
22
()()
22
qq
xa xb
Mq q
−−
=−
.
y
М
0
F
q
-q
x
x
L
M
a
F
a
q
a
q
b
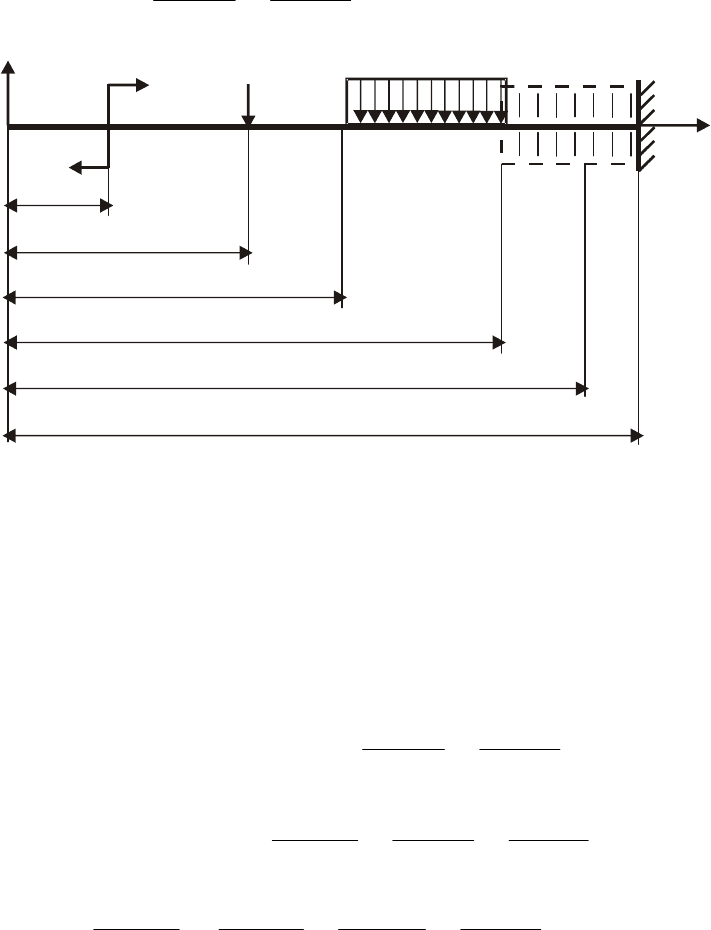
Рис. 7.14. Условная схема нагружения балки при изгибе
Рассмотрим балку длиной , нагруженную парой сил l
0
M
, силой и
распределенной нагрузкой интенсивностью (рис. 7.14). Расстояния от левого
конца балки до нагрузок
F
q
0
M
,
F
, обозначим соответственно , q
m
a
F
a , — до
начала распределенной нагрузки, — до конца распределенной нагрузки. Начало
координат возьмем на левом конце балки.
q
a
q
b
Для сечения, взятого на последнем участке балки, уравнение изгибающего момента
имеет вид
22
0
0
()(
() ( ) ( )
22
−−
′′
==−−−− +
qq
zy m F
)
x
axb
EJ u M x M x a F x a q q
.
Интегрируя это уравнение, получаем уравнение углов поворота сечений
33
2
0
()()
()
() ( )
266
−−
−
′
==−− − + +
qq
F
zy z m
xa xb
xa
E
Ju EJ x M x a F q q C
θ
.
Интегрируя еще раз, получаем уравнение прогибов балки
44
23
0
()()
()()
()
2 6 24 24
−−
−−
=−−++
qi q
mF
zy
xa xb
xa xa
+
E
Ju x M F q q Cx D.
Уравнения для других участков, согласно определению изгибающего момента,
должны включать только слагаемые от нагрузок, находящихся по одну сторону
(слева) от рассматриваемого сечения.
Определим смысл произвольных постоянных.
74
При 0x =
0z
E
JC
θ
=
0zy
E
Ju D
=
.
Откуда
0
z
C
E
J
θ
=
0y
z
D
u
E
J
=
,
где и
0y
u
0
θ
— прогиб и угол поворота сечения балки в начале координат.
В общем виде для случая действия любого количества нагрузок уравнение упругой
линии балки принимает вид
23
00 0
44
() ()
26
() ()
24 24
−−
=++ +
−−
+−
∑∑
∑∑
mF
zy zy z
qi q
xa xa
EJ u EJ u EJ x M F
xa xb
qq
θ
+
(7.15).
Это уравнение называется универсальным уравнением упругой линии балки или
уравнением Крылова.
Данное уравнение составлено с учетом распределенной нагрузки постоянной
интенсивности . Если используется распределенная нагрузка переменной
интенсивности надо добавить слагаемые, содержащие первую, а если надо, то и
вторую производную от .
q
()qx
()qx
Правила пользования уравнением Крылова
1. Начало координат всегда на левом конце балки. В этом случае знаки прогиба и
угла поворота сечения совпадают, в противном случае знаки противоположны.
2. Составить уравнение Крылова для последнего участка балки. Уравнение для
произвольного сечения балки должно включать в себя только слагаемые от
нагрузок, находящихся слева от рассматриваемого сечения. Желательно
записывать нагрузки в том порядке, в каком они стоят на балке, соблюдая форму
записи, приведенную в уравнении (7.15).
3. Уравнение углов поворота сечений получается из уравнения прогибов путем
дифференцирования.
4. Знак перед каждым слагаемым соответствует знаку изгибающего момента от
данной нагрузки.
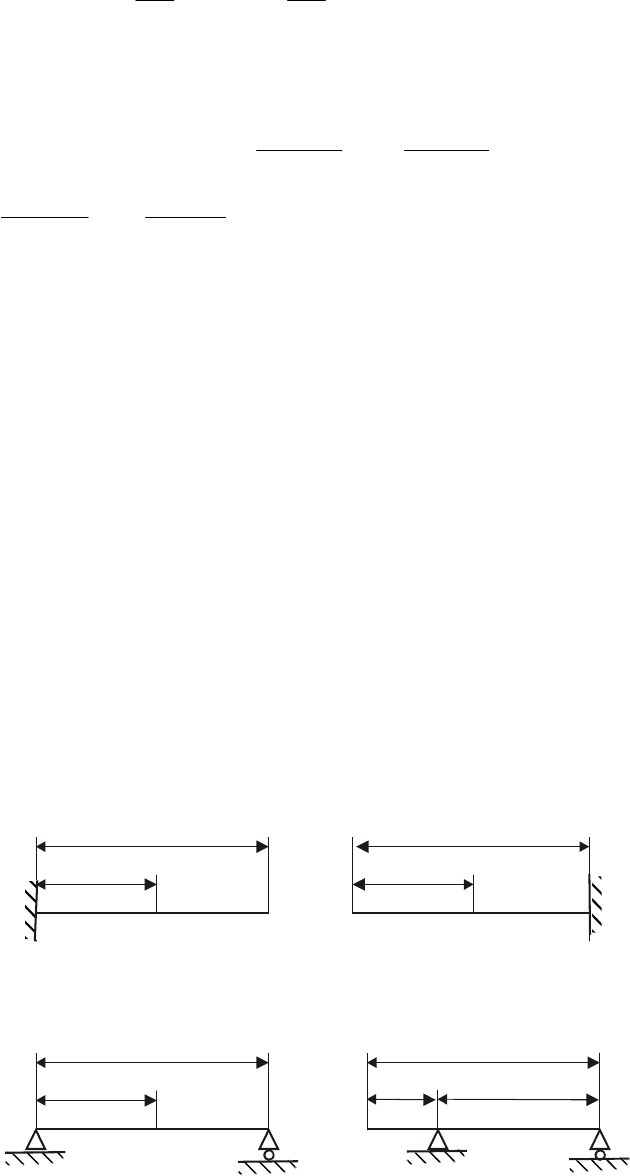
5. Начальные параметры и
0y
u
0
θ
определяются из граничных условий
(рис. 7.15).
x
L
u(0)=0
u(0)=0
/
x
L
u(L)=0
u(L)=0
/
x
L
u(0)=0
u
(
L
)
=0
x
L
u(a)=0
u
(
a+L
)
=0
а
Рис. 7.15. Граничные условия для определения перемещений балки при изгибе
7.5 Изгиб кривых брусьев
Нормальные напряжения в кривых брусьях
В кривых брусьях нормальные напряжения изменяются по гиперболическому закону
(рис. 7.16), а нейтральная ось смещена в сторону центра кривизны на малую
величину . По мере увеличения радиуса кривизны бруса гипербола распрямляется,
приближаясь к прямой линии, а нейтральная ось приближается к центру тяжести.
e
Различают кривые брусья большой и малой кривизны.
75
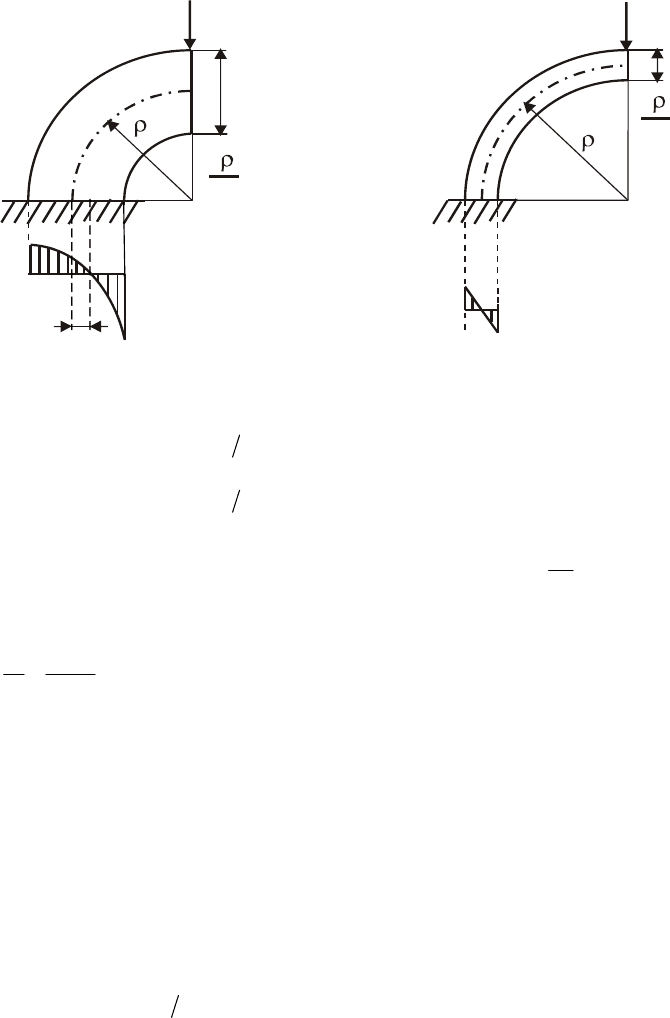
е
F
h
гипербола
F
h
прямая
а)
б)
h
<5
h
>5
min
σ
max
σ
min
σ
max
σ
Рис. 7.16. Брусья большой и малой кривизны
Брусом большой кривизны считается брус, у которого отношение радиуса кривизны к
высоте поперечного сечения
5h
ρ
<
(рис. 7.16, а).
Брусом малой кривизны считается брус, у которого отношение радиуса кривизны к
высоте поперечного сечения
5h
ρ
> (рис. 7.16, б).
При расчете на прочность брусьев малой кривизны можно использовать формулу
нормальных напряжений, выведенную для прямых балок
M
y
J
σ
= . При этом
погрешность расчета менее 5%.
У брусьев большой кривизны нормальные напряжения определяются по формуле
N
MS
Ary
σ
⋅
=+
+
, где — статический момент площади сечения относительно
нейтральной оси, — радиус кривизны нейтральной оси, — расстояние от
нейтральной оси до точки, где определяются напряжения.
S
r y
В некоторых случаях, например, для диска с отверстием, максимальные напряжения
могут примерно вдвое превышать напряжения, найденные по формуле, используемой
для прямых брусьев.
На практике брусья большой кривизны встречаются довольно редко. В качестве
примера брусьев большой кривизны можно привести крюк подъемного крана или
звено якорной цепи. Расчет напряжений в брусьях большой кривизны не
представляет большого практического интереса.
В курсе сопротивления материалов рассматривается прочность и жесткость в
основном длинных и тонких стержней. Напомним, что формула для нормальных
напряжений в прямых брусьях справедлива лишь при отношении длины к высоте
поперечного сечения
10hb> . В дальнейшем для расчета кривых брусьев малой
кривизны будем использовать формулу нормальных напряжений, выведенную для
прямых брусьев.
Внутренние усилия в кривых брусьях
Рассмотрим определение внутренних усилий в кривых брусьях. Внутренние усилия
определяются методом сечений из условия равновесия отсеченной части стержня.
При плоском изгибе кривого бруса в поперечных сечениях возникают три
внутренних усилия: продольное усилие
N
, поперечная сила и изгибающий
момент
Q
M
. Найдем внутренние усилия в брусе, геометрическая ось которого
представляет собой четверть круга (рис. 7. 17).
Мысленно разрежем стержень произвольным сечением, полярные координаты
которого и
ρ
ϕ
. Действие отброшенной правой части в выбранном сечении заменим
силой
F
и парой сил
M
. Силу
F
раскладываем на две составляющие: вдоль оси
бруса
N
и по касательной к сечению Q ()NFSin
ϕ
=
⋅ и (QFCos)
ϕ
=
⋅ .
76

F
F
F
Q
N
F
F
N
F
Q
М
φ
(
Sin
ρφ)
F
ρ
М
Рис. 7.17. Внутренние усилия в кривом брусе
Пара сил
M
является изгибающим моментом в сечении и определяется как
произведение силы на плечо
()MF Sin
ϕ
ρ
ϕ
=
⋅⋅ , где плечо есть перпендикуляр,
опущенный из центра тяжести рассматриваемого сечения на линию действия силы.
Эпюры
,,
N
QM показаны на рис. 7.17 .
Для брусьев малой кривизны влиянием продольного усилия и поперечной силы
обычно пренебрегают и эпюры
N
и Q не строят.
Если на кривой брус действует распределенная нагрузка, то ее обычно представляют
в виде суммы двух проекций нагрузки интенсивностью на две оси (в нашем случае
и ).
q
y z
x
а
q
x
q
q
q
(Sinρφ)
φ
φ
Рис. 7.18. Кривой брус, нагруженный распределенной нагрузкой
На рисунке 7.18 представлен брус, криволинейная часть которого нагружена
нагрузкой
, равномерно распределенной по радиусу.
На криволинейном участке бруса 0
π
ϕ
<
<
2
222 2
() (1 ())
(1 ( ))
22
qx qy
Sin Cos
MM M q q q Cos
ϕ
ρϕρ ϕ
ρ
ϕ
2
⋅⋅−
=+= + = −
.
На прямолинейном участке бруса
0
x
a
<
<
)
2
xqxqy
M
MMq q x
ρρ
ρ
2
=+= +(+
2
.
77
7.6 Расчет балок на упругом основании
В инженерной практике часто встречаются балки, лежащие на упругом основании. К
таким балкам относятся шпалы железнодорожного пути, ленточные фундаменты
зданий, фундаменты плотин и так далее.
Сюда же можно отнести и рельсы, у которых число опор велико, а расстояние между
ними мало по сравнению с длиной рельсов. расчет балки на упругом основании не
может быть выполнен с помощью уравнений равновесия.
Эта задача является статически-неопределимой. Величина реакции в каждой точке
зависит от прогиба балки, а прогиб балки в свою очередь зависит от реакции со
стороны основания.
Для решения задачи примем гипотезу о пропорциональной зависимости между
реакцией и осадкой основания, впервые предложенную академиком Н.И.Фуссом и
использованной Е. Винклером для расчета балок на упругом основании.
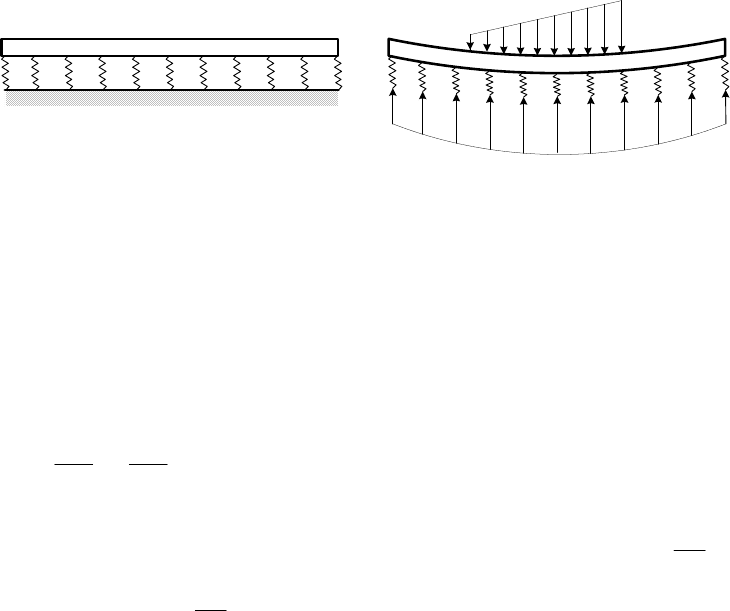
Согласно модели Винклера реальное основание как бы заменяется бесконечным
числом упругих, не связанных между собой пружин (рис. 7.19). Реакция
R
в каждой
точке основания балки будет пропорциональна прогибу в этой точке, равному
осадке основания
u
R
kbu=⋅⋅,
где — ширина балки, — коэффициент жесткости упругого основания,
называемый также коэффициент постели. Экспериментально он определяется путем
вдавливания в грунт жесткого штампа. Так для песчаного грунта
b k
15k =− МН/м
3
— песок рыхлый,
10 100k =− МН/м
3
— песок утрамбованный,
250k < — песок слежавшийся.
q(x)
R(x)=kbu
Рис. 7.19. Балка на упругом основании (модель Винклера)
С учетом внешней нагрузки и реакции упругого основания суммарная интенсивность
распределенной нагрузки в некоторой точке балки
p
qRqkbu=−=− .
Для получения дифференциального уравнения балки на упругом основании
используем последнее из уравнений (7.14)
IV
z
E
Ju p q kbu==− . Откуда
IV
z
E
Ju kbu q+= или
IV
zz
kb q
uu
E
JEJ
+=
(7.16).
Решая уравнение (7.16), находим перемещения балки , по перемещениям
определяем угол поворота сечения
u
u
′
θ
= , изгибающий момент
z
u
M
E
J
′′
=
и
поперечную силу
z
u
Q
E
J
′′′
=
.
Вот, собственно говоря, и вся теория расчета балок на упругом основании.
Все, что имеется в литературе по этому вопросу, относится к способам решения
дифференциального уравнения четвертого порядка. Но ведь Mathcad сам в состоянии
решить такое уравнение. Примеры расчета балок на упругом основании приведены в
электронной книге в разделе
для главы 7.
78
Глава 8. Учет пластических деформаций
В предыдущих главах расчеты на прочность велись с учетом только упругих
деформаций. В этой главе будет рассмотрено влияние пластических деформаций на
прочность конструкций. Вначале рассмотрим распределение напряжений в сечении
стержня при упругопластической деформации растяжения-сжатия, изгиба, кручения.
Затем рассмотрим приближенные методы оценки предельной нагрузки на стержень.
8.1 Связь напряжений и деформаций
В разделе 5.4 рассматривалось построение диаграммы истинных напряжений при
растяжении. Для расчетов конструкций на прочность необходимо получить
уравнение этой диаграммы. С этой целью используют четыре вида аппроксимации
диаграммы деформирования.
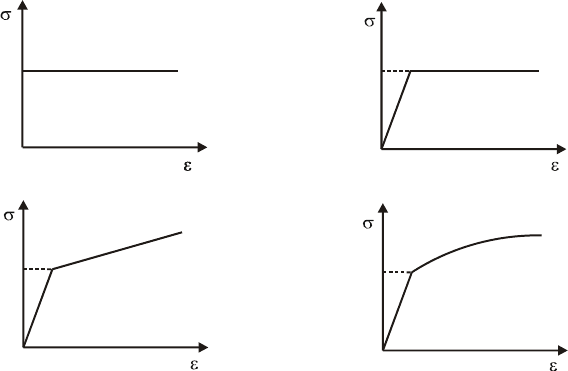
Диаграмма идеального упругопластического тела (диаграмма Прандтля)
(рис. 8.1б) с бесконечно длинной площадкой текучести. Используется для
материалов с площадкой текучести на диаграмме.
При
т
ε
ε
<
E
σ
ε
=⋅,
При
т
ε
ε
≥
т
σ
σ
=
Диаграмма упругопластического тела с линейным упрочнением (рис. 8.1в).
Используется для материалов, не имеющих площадки текучести на диаграмме.
При
т
ε
ε
<
E
σ
ε
=⋅,
При
т
ε
ε
≥
т 1 т
()E
σ
σεε
=+⋅− ,
Где
1
0,01≈
E
E — модуль упрочнения;
Диаграмма упругопластического тела со степенным упрочнением (рис. 8.1г). В
расчетах конструкций используется редко, так как не вносит существенных
изменений в распределение напряжений в конструкции, но усложняет
проведение расчетов.
При
т
ε
ε
< , Eσ= ⋅ε
При
т
ε
ε
≥
т
m
A
σ
σε
=+⋅,
Где и — эмпирические коэффициенты. A m
Получение уравнений для линейной и степенной аппроксимаций показано в примере
к главе 5
Построение диаграммы деформирования в электронной книге.
Линейная апроксимация заменяет рассматриваемый участок диаграммы прямой
линией. Степенная апроксимация — кривой.
В добавление к трем указанным видам аппроксимации введем еще один:
Диаграмма деформирования идеального жесткопластического тела,
представляющая собой одну горизонтальную линию
т
σ
σ
=
(рис.8.1а). При
т
σ
σ
< деформация
ε
=0, то есть материал считается абсолютно жестким
(недеформируемым). При
т
σ
σ
=
деформация
ε
→∞.
Последний вид аппроксимации используется в расчетах технологических процессов
обработки металлов давлением и в расчетах конструкций по предельным нагрузкам.
0
а
)
0
б)
0
в)
0
г)
т
σ
т
σ
т
σ
т
σ
79

Рис. 8.1. Виды аппроксимации диаграммы деформирования
8.2 Учет пластических деформаций при
растяжении-сжатии
При растяжении-сжатии распределение деформаций и напряжений по сечению
стержня равномерное, то есть
Const
σ
=
и Const
ε
=
.
При растяжении-сжатии, как упругом, так и упругопластическом, нормальные
напряжения во всех точках сечения одинаковы. Справедлива формула для
напряжения
N
A
σ
= .
В статически определимых задачах из условий равновесия определяются продольные
усилия
N
, а по ним напряжения
σ
. Определить удлинения стержней по старой
формуле
N
L
L
E
A
Δ=
, основанной на законе Гука, уже нельзя. Надо по диаграмме
деформирования, зная напряжения, найти деформацию
L
L
ε
Δ
= и по ней определить
удлинение .
LΔ
В статически неопределимых задачах под действием пластических деформаций
происходит перераспределение напряжений, что ведет к изменению условий
равновесия системы. Пример расчета напряжений с учетом пластических
деформаций в статически неопределимой шарнирно-стержневой системе приведен в
электронной книге в разделе
Для главы 8.
8.3 Учет пластических деформаций при изгибе
При изгибе статически определимых балок изгибающий момент определяется
методом сечений, как указано в главе 2, независимо от величины деформации.
Характер распределения напряжений в поперечных сечениях балки оказывается
различным при упругих и упругопластических деформациях.
ВАЖНАЯ ГИПОТЕЗА
В теории пластичности принято, что
гипотеза плоских сечений справедлива
как при упругих, так и упругопластических деформациях балки.
Это положение является основным при расчетах балок в упругопластической
области, без принятия гипотезы о распределении деформаций расчет оказывается
невозможным.
На основании этой гипотезы можно считать, что при изгибе по высоте сечения
деформации распределены по линейному закону, как при упругой, так и при
упругопластической деформации (рис. 8.2).
Для определения напряжений при упругопластической деформации надо по
диаграмме деформирования для заданного значения деформации
ε
определить,
соответствующее ей значение напряжения
σ
. Величина этого напряжения будет
зависеть от выбранного вида аппроксимации диаграммы деформирования (рис. 8.2).
пластическая
зона
h
y
пластический
шарнир
т
ε
max
ε
т
σ
max
σ
т
σ
т
σ
b
упругая
зона
y
Т
Рис. 8.2 Распределение деформаций и напряжений при упругопластическом изгибе балки
Будем постепенно увеличивать нагрузку на балку и соответственно изгибающий
момент
.
При чисто упругой деформации напряжения в сечении распределены по линейному
закону
, пока на поверхности балки они не достигнут предела текучести
max т
σ
σ
= .
Найдем предельный изгибающий момент при упругой деформации
80
