Макаров Е.Г. Сопротивление материалов
Подождите немного. Документ загружается.

Q
A
τ
=
()
arct
g
G
0
П
S
l
Δ
γ=
S
Δ
Q
внеш
W
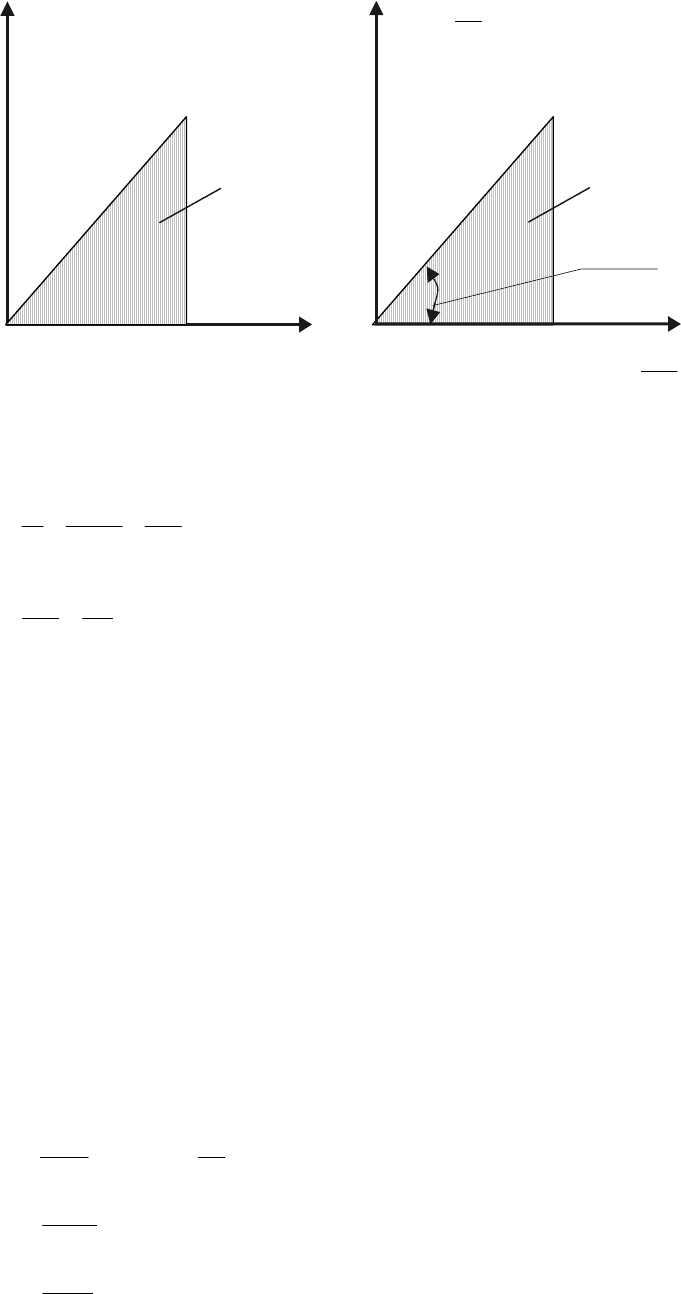
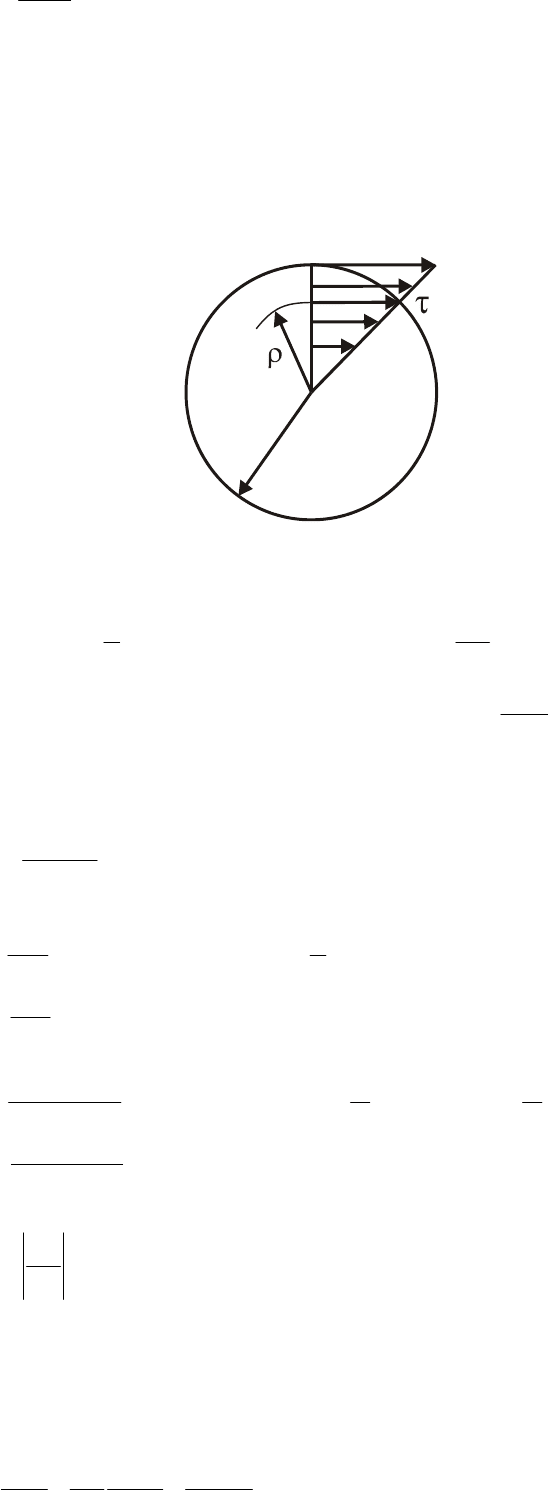
Рис. 6.2. Работа внешних сил при сдвиге
Удельная потенциальная энергия
0
П
, накопленная в единице объема V ,
0
2
П QS
П
VAl
τ
γ
⋅Δ ⋅
== =
2
.
Или, с учетом,
G
τ
γ
=⋅
0
2
2
⋅
==
2
П
G
τ
γτ
(6.4).
Величина
0
П
численно равна площади диаграммы деформирования при сдвиге в
координатах
τ
γ
−
(рис. 6.2).
ПРИМЕЧАНИЕ
Сдвиг — это деформация без разрушения материала. Разрушение при сдвиге носит
название срез.
В заключение ведем понятие чистого сдвига.
Чистым называется сдвиг, при котором в поперечных сечениях отсутствуют
нормальные напряжения. При сдвиге, вызванном двумя силами, направленными
навстречу друг другу, материал в промежутке между силами, кроме сдвига, еще
испытывает изгиб, вызывающий появление нормальных напряжений. Примером
чистого сдвига является кручение.
6.2 Расчет простейших соединений
Приведенных сведений о расчетах на растяжение-сжатие и на сдвиг достаточно для
расчета на прочность простейших соединений, таких как болты, штифты, заклепки,
сварные швы и другие.
В основе расчета лежат условия прочности на растяжение, срез и смятие.
т
раст раст
раст
n
F
A
σ
σσ
⎡⎤
=≤ =
⎣⎦
среза среза раст
среза
(0,5 0,6)
F
A
ττ
⎡⎤ ⎡
=≤ ≈−
⎣⎦ ⎣
σ
⎤
⎦
[]
смят смят раст
смят
2
F
A
σσ
⎡
=≤ ≈
⎣
σ
⎤
⎦
Здесь
F
— сила, вызывающая деформацию тела, , , —площади
поперечных сечений, испытывающих деформацию соответственно растяжения,
среза, смятия. Выбор этих площадей будет далее пояснен на конкретных примерах.
раст
A
среза
A
смят
A
Допускаемые напряжения на растяжение, срез, смятие выбираются с учетом
опытных данных, позволяющих получить достаточно достоверные результаты.
В основе всех трех условий прочности лежит предположение о равномерности
распределения напряжений по всему сечению. Если при растяжении подобная
гипотеза справедлива (вдали от места приложения нагрузки), то в случае расчета на
срез и смятие это не верно, но … удобно и, учитывая приближенный характер
расчетов, возможно.
Расчеты простейших соединений слишком просты, чтобы использовать Mathcad, и
выполняются с использованием микрокалькулятора. Однако при наличии готовой
программы можно ею воспользоваться. В электронной книге в разделе
Для главы 6
51
приведена программа расчета простейших соединений. Обратите внимание на форму
записи условия прочности в Mathcad.
6.2.1. Расчет тяги
Схема соединения показана на рис. 6.3. Требуется определить из условия прочности
диаметр тяги , диаметр
d
D
и высоту головки тяги при заданной силе h
F
,
растягивающей тягу.
d
h
D
F
d
d
h
раст
A
смят
A
среза
A
D
d
Рис. 6.3. Схема тяги
Примером тяги может служить болтовое соединение. Но болт имеет резьбу, в
которой возникает концентрация напряжений. Как указано в разделе 1.14.1 при
статическом нагружении влиянием концентрации напряжений можно пренебречь.
При расчете болтовых соединений в курсе Деталей машин влияние резьбы
учитывается поправочным коэффициентом.
Растяжение тяги
Диаметр тяги найдем из условия прочности на растяжение
т
раст раст
раст
n
F
A
σ
⎡⎤
σ= ≤σ =
⎣⎦
.
Площадь сечения, где возможен разрыв тяги
2
раст
4
d
A
π
= .
Из условия прочности
раст
раст
F
A ≥
⎡
⎤
σ
⎣
⎦
.
Приравнивая два выражения для , находим диаметр тяги
раст
A
раст
раст
4
4
A
F
d ≥=
π
⎡⎤
πσ
⎣⎦
.
Найденный результат округляем в большую сторону, как правило, до целых
миллиметров.
Смятие головки тяги
Диаметр головки тяги найдем из условия смятия
[]
смят смят раст
смят
2
F
A
σσ
⎡⎤
=≤ ≈
⎣⎦
σ
.
В качестве площади смятия берем площадь опирания головки на лист металла
()
22
смят
ADd
π
=−
4
.
Из условия прочности
[]
смят
смят
F
A
σ
= .
Приравнивая два выражения для , находим диаметр
смят
A
D
.
Срез головки тяги
Высоту головки тяги
h найдем из условия прочности на срез
среза среза раст
среза
(0,5 0,6)
F
A
ττ
⎡⎤ ⎡
=≤ ≈−
⎣⎦ ⎣
σ
⎤
⎦
В качестве площади среза берем цилиндрическую поверхность диаметром и
высотой , которая образовалась бы при протаскивании головки тяги через
отверстие в листе металла
d
h
среза
=
Adh
π
.
Из условия прочности
среза
среза
F
A
τ
≥
⎡
⎤
⎣
⎦
.
Приравнивая два выражения для , находим высоту головки .
среза
A h
52

6.2.2. Расчет штифта (заклепки)
Условия нагружения заклепок при заклепочном соединении двух листов металла и
штифтов, соединяющих, например, обод зубчатого колеса с корпусом в планетарном
редукторе, практически одинаковы. Схема штифтового соединения показана на
рис. 6.4.
d
h
d
d
h
F
F
смят
А
среза
А
Рис. 6.4. Схема штифтового соединения
Расчет штифта на срез
Из условия прочности на срез
среза
среза
F
A
τ
≥
⎡
⎤
⎣
⎦
.
.Штифт может срезаться по круглому поперечному сечению.
Площадь среза
2
среза
4
d
A
π
.
Приравнивая два выражения , определяем диаметр штифта .
среза
A d
Расчет на смятие
Из условия смятия находим допускаемую площадь смятия
[]
смят
смят
F
A
σ
≥ .
Реальная площадь смятия определяется толщиной скрепляемых штифтом деталей.
Истинная поверхность смятия —это зона контакта листа металла и штифта на
поверхности цилиндра, но размер ее и распределение напряжений на ней неизвестно.
Напряжения на поверхности контакта распределяются по сложному степенному
закону.
Удовлетворительные результаты расчета получаются, если взять в качестве площади
смятия проекцию криволинейной поверхности цилиндра на диаметральную
плоскость , где
h — наименьшая из толщин соединяемых деталей.
смят
Adh=⋅
Если детали разной прочности, то возможно потребуется проверка прочности на
смятие обеих деталей.
Приравнивая два выражения , находим допустимую толщину детали .
смят
A h
Обычно толщина листов задана, тогда диаметр штифта или заклепки определяется
дважды (из условий прочности на срез и на смятие). Окончательно принимают
диаметр , удовлетворяющий обоим условиям прочности.
Расчет заклепочного соединения абсолютно аналогичен расчету штифтового
соединения.
6.2.3. Расчет сварного соединения
Рассмотрим приварку пластины к листу угловым швом с обваркой по всему контуру
(рис.6.5).
b
F
?
F
F
45
0
l
Рис. 6.5. Схема сварного соединения
Расчет пластины на растяжение
Сначала найдем необходимую ширину пластины . Из условия прочности на
растяжение
b
раст
раст
F
A
σ
≥
⎡⎤
⎣⎦
.
53

Реальная толщина пластины
раст
Ahb
=
⋅ .
Приравнивая два выражения для , находим ширину пластины .
раст
A b
Расчет длины сварного шва
Из условия среза сварного шва найдем допускаемую площадь среза
среза
среза
F
A
τ
≥
⎡⎤
⎣⎦
.
Считается, что срез сварного шва происходит по наименьшей площади среза
, где — длина перпендикуляра, опущенного из вершины шва на его
поверхность,
среза
At=⋅Lt
2Llb
=
+ — полная длина контура обварки пластины,
Для равнобокого шва поверхность среза наклонена под углом 45° к плоскости листа.
Тогда площадь среза шва
среза
cos 45°AL
δ
=
⋅ , где
δ
— высота катета сварного
шва, обычно равная толщине листа.
Приравнивая два выражения для , находим длину накладки пластины на
лист.
среза
A l
Учитывая, что при подобных расчетах простейших соединений погрешность расчета
велика, в реальных расчетах обычно вводится ряд поправочных коэффициентов,
учитывающих специфику работы соединения.
6.3 Кручение стержней круглого поперечного
сечения
Кручение — один из 4-х видов простых деформаций. При кручении стержень
нагружен только парами сил, вращающими стержень вокруг продольной оси
x
. При
этом в поперечных сечениях стержня действует только одно внутреннее усилие —
крутящий момент,
к
x
M
M= , численно равный сумме моментов всех сил,
расположенных по одну сторону от рассматриваемого сечения.
Знак крутящего момента обычно безразличен, так как прочность стержня при
кручении зависит только от величины крутящего момента и не зависит от его
направления. Тем не менее, для упорядочения расчетов в ряде учебников
рекомендуется считать крутящий момент положительным, если при взгляде со
стороны любого конца стержня мы видим внешний закручивающий момент,
действующим против часовой стрелки.
В технике наиболее часто используются стержни круглого или кольцевого
поперечного сечения. Оказывается и расчет таких стержней на кручение значительно
проще, чем стержней с другой формой поперечного сечения. С этого случая и начнем
изучение деформации кручения стержней.
до де
ф
о
р
мации
М
после деформации
Рис. 6.6. Деформация прямоугольной сетки при кручении стержня
Рассмотрим результат следующего эксперимента. На поверхность резинового
стержня круглого поперечного сечения нанесем прямоугольную сетку (рис. 6.6).
Нагрузим стержень парой сил, закручивающей стержень вокруг продольной оси.
При этом поперечные сечения стержня поворачиваются относительно друг друга, и
нанесенная сетка линий искажается. Первоначально прямоугольные элементы сетки
становятся параллелограммами.
Изменение формы элемента сетки свидетельствует о деформации сдвига,
происходящей при кручении стержня круглого поперечного сечения.
6.3.1. Касательные напряжения и угол закручивания
Основные гипотезы
Вывод формул для напряжений и перемещений при кручении начнем с гипотез,
принимаемых для упрощения расчетов.
ЗАМЕЧАНИЕ
Справедливы все гипотезы из раздела 1.9. Далее рассмотрим только гипотезы,
непосредственно используемые при выводе указанных формул.
54
Расстояние между поперечными сечениями при кручении не меняется.
Следовательно, деформация волокон стержня вдоль продольной оси
x
равна
нулю
x
ε
=0 и по закону Гука
x
x
E
σ
ε
=
нормальные напряжения в поперечных
сечениях стержня отсутствуют
x
σ
=
0.
При кручении прямолинейные радиусы не искривляются, а только
поворачиваются.
Круглое сечение остается круглым. Касательные напряжения
перпендикулярны радиусам вращения.
τ
Это аналог гипотезы плоских сечений. Стержень рассматриваем как набор
жестких дисков, поворачивающихся друг относительно друга.
Волокна друг на друга не давят.
Следовательно, нормальные напряжения в поперечном направлении
отсутствуют
0
yz
σ
σ
==.
у
z
х
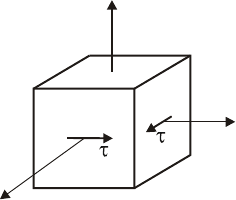
Рис. 6.7. Напряжения на гранях элемента при кручении
Итак на гранях элемента стержня, вырезанного плоскостями, перпендикулярными
осям
x
, , , отсутствуют нормальные напряжения y z
σ
и действуют только
касательные
τ
(рис. 6.7). Такой случай нагружения называется чистым сдвигом.
Следовательно, кручение — частный случай чистого сдвига и все зависимости,
полученные при рассмотрении деформации сдвига, могут быть использованы при
кручении стержней.
Порядок вывода расчетных формул в сопротивлении материалов
При выводе любых аналитических зависимостей в сопротивлении материалов
рассматриваются условия существования малого элемента тела с целью
последовательного определения его перемещений, деформаций и напряжений в нем.
Далее проинтегрировав установленные зависимости по объему тела, находят связь
напряжений с внешними силами.
Всякий расчет состоит из 4-х этапов.
1. Геометрический анализ. На этом этапе устанавливается связь между
перемещениями и деформациями малого элемента тела.
2. Физический анализ — устанавливает связь между деформациями элемента и
напряжениями в нем. При упругой деформации используется закон Гука.
3. Статический анализ — устанавливает связь напряжений с внешними
нагрузками путем интегрирования уравнений равновесия элемента по всему
объему тела с учетом граничных условий на поверхности. В сопротивлении
материалов в роли таких интегралов выступают условия эквивалентности
напряжений и внутренних усилий, установленные в разделе 1.4.
4. Синтез установленных зависимостей. Подставляя одно в другое выражения,
найденных на трех предыдущих этапах, и упрощая их, получают окончательные
расчетные формулы.
Вывод расчетных формул для напряжений и угла закручивания стержня
Геометрический анализ.
Вырежем из стержня, испытывающего деформацию кручения (рис. 6.8) элемент
длиной . В этом элемента на некотором расстоянии
dx
ρ
от центра кручения
выделим волокно и рассмотрим его перемещение.
ab
55
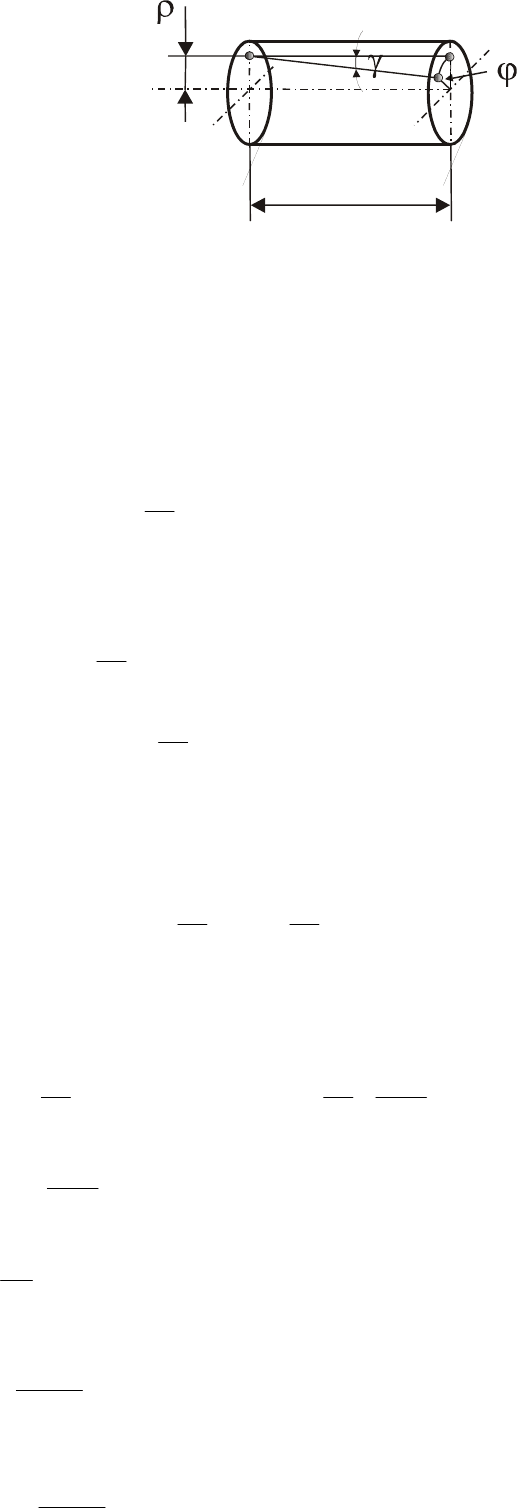
dx
а
b
b
1
о
Рис.6.8. Элемент стержня, работающего на кручение
В процессе деформации крайние поперечные сечения элемента поворачиваются
относительно друг друга. Мысленно остановим левое сечение. Тогда правое сечение
повернется относительно него на угол
dx
d
ϕ
. При этом волокно поворачивается на
угол сдвига
ab
γ
и приходит в положение .
1
ab
Найдем связь между углом поворота сечения
d
ϕ
и углом сдвига волокна
γ
.
Перемещение правого конца волокна (точки )
b
1
bb d dx
ρ
ϕγ
=⋅ = ⋅.
Откуда
d
dx
ϕ
γ
ρ
= (6.5).
Физический анализ
Так как кручение — это частный случай чистого сдвига, при упругой деформации
для связи деформаций и напряжений используем закон Гука при сдвиге с учетом
выражения (6.5)
d
GG
dx
ϕ
τγρ
=⋅= (6.6).
Формула для касательных напряжений получена, но пользоваться ею нельзя, так как
неизвестна величина
d
dx
ϕ
. Однако логика подсказывает, что чем больше крутящий
момент
к
M
, тем больше угол закручивания стержня
ϕ
.
Статический анализ
Воспользуемся условием эквивалентности напряжений и внутренних усилий для
связи касательных напряжений с крутящим моментом. Крутящий момент есть
результат действия касательных напряжений в поперечном сечении стержня
2
к
AA A
dd
M
dA G dA G dA
dx dx
ϕϕ
τρ ρ ρ ρ
=⋅⋅= =
∫∫ ∫
(6.7).
В выражении (6.7) за знак интеграла вынесены величины постоянные, независящие
от выбора площадки . Выражение под интегралом представляет собой полярный
момент инерции поперечного сечения
dA
2
p
A
J
dA
ρ
=
∫
. Тогда
к
p
d
M
GJ
dx
ϕ
= . Откуда
к
p
GJ
M
d
dx
ϕ
=
⋅
(6.8).
Подставив выражение (6.8) в выражение (6.6), находим
p
к
GJ
M
G
τρ
=⋅
⋅
.
Сократив это выражение на модуль сдвига , окончательно получаем
G
к
p
J
M
τ= ρ
(6.9).
Формулу для угла закручивания стержня получаем путем интегрирования выражения
(6.8)
p
к dx
GJ
l
M
ϕ
⋅
=
⋅
∫
,
где — длина стержня. l
Если на стержень действуют несколько внешних нагрузок, то
p
к dx
GJ
l
M
ϕ
⋅
=
⋅
∑
∫
(6.10),
где сумма берется по числу участков на стержне. Границами участков являются
сечения, где либо приложены нагрузки, либо изменяются форма и размеры
поперечного сечения.
Если крутящий момент по длине участка не меняется, то интеграл принимает вид
суммы
56
к
p
GJ
M
l
ϕ
⋅
=
⋅
∑
(6.11),
где — длина соответствующего участка, сумма берется по количеству участков.
l
Условие прочности при кручении
Построим эпюру распределения касательных напряжений по сечению круглого
стержня при кручении. В соответствии с формулой (6.9) касательные напряжения
распределены по сечению по линейному закону и пропорциональны радиусу
ρ
(рис. 6.9).
max
τ
max
ρ
Рис. 6.9. Касательные напряжения в круглом сечении при кручении
При
ρ
=0 (в центре круга) —
τ
=
0 .
При
max
2
d
ρρ
== (на поверхности круга) —
к
max max
p
M
J
ττ ρ
==
Введем новую геометрическую характеристику сечения
max
p
p
J
W
ρ
= ,
Где
p
W — момент сопротивления при кручении или полярный момент
сопротивления.
Тогда на поверхности стержня
к
max
max
p
M
W
τ
= (6.12).
Для круглого поперечного сечения
4
4
0,1
32
p
d
J
d
π
=≈
max
2
d
ρ
=
3
3
0, 2
16
p
d
W
π
=≈
d
(6.13).
Для кольца
4
4
(1 )
0,1 (1 )
32
4
4
−
=≈
p
D
J
πα
−
D
α
d
D
α
=
max
2
D
ρ
=
3
3
(1 )
0, 2 (1 )
16
4
4
−
=≈
p
D
WD
πα
−
α
(6.14).
Условие прочности при кручении
[
]
max
τ
τ
≤ или с учетом (6.12)
[] [ ]
к
max
p
(0,5 0,6)
W
=≤≈−
M
τ
τσ
(6.15).
6.3.2 Потенциальная энергия при кручении стержня
Потенциальная энергия упругой деформации, численно равная работе внешних сил,
может быть определена как площадь диаграммы деформирования. При упругой
деформации — это площадь треугольника (рис. 6.10). Если стержень нагружен одной
парой сил, то с учетом выражения (6.11)
2
ккк к
22 2
p
p
M
MMl Ml
П
GJ GJ
ϕ
== =
⋅⋅
.
57

M
k
W
внеш
=П
Рис.6.10. Диаграмма деформирования при кручении
В общем случае действия произвольной нагрузки, если
к
M
Const
≠
2
к
2
p
l
M
dx
П
GJ
=
⋅
∫
(6.16).
Рассмотрим второй (более общий) способ определения потенциальной энергии
упругой деформации
П
. Найдем ее как интеграл по объему от удельной
потенциальной энергии
V
0
П
0
V
П
П dV=
∫
.
С учетом ,
dV dA dx=⋅
2
0
2
П
G
τ
γτ
⋅
==
2
и
к
p
J
τ
ρ
Μ
=
22
кк
22
1
22
2
lA lA l A
pp
MM
П
dA dx dA dx dA dx
GG
JGJ
τ
ρρ
2
22
=⋅=⋅=⋅
⋅
∫∫ ∫∫ ∫ ∫
.
Так как
2
p
A
J
dA
ρ
=
∫
, то
2
к
2
p
l
M
П
dx
GJ
=
⋅
∫
,
что совпадает с выражением (6.16).
В случае действия нескольких нагрузок
2
к
2
p
l
M
П
dx
GJ
=
⋅
∑
∫
(6.17).
Здесь сумма берется по количеству участков.
6.4. Связь между крутящим моментом,
мощностью и скоростью вращения вала
При расчете электропривода различных устройств, исходя из нагрузки на
исполнительный орган, например, станок, требуется определить мощность
электродвигателя.
ред
у
ктор
электродвигатель
станок
Рис. 6.11. Схема электропривода
На рисунке 6.13 изображена схема электропривода, где вращение электродвигателя
через муфту и редуктор передается на станок.
Найдем связь между крутящим моментом на валу исполнительного органа и
мощностью двигателя. Зная необходимый крутящий момент на валу станка и
передаточное отношение редуктора, определяем момент на входном валу редуктора,
а затем мощность электродвигателя.
Мощность
N
— это работа внешних сил в единицу времени
внеш
W t
внеш
=
W
N
t
.
58
Работа пары сил
к
M
на угле поворота вала
ϕ
внеш
к
=
⋅WM
ϕ
.
Откуда
внеш
кк
===
WMM
N
tt
ϕ
ω
,
Где
t
ϕ
ω
= — угловая скорость вращения вала
Угловая скорость
ω
связана с числом оборотов вала в минуту зависимостью n
2
60
n
π
ω
= . Тогда мощность
к
2
60
n
NM
π
= , откуда
к
60
9,65
2
N
N
M
nn
π
=≈ Нм, если мощность
N
введена в ваттах, то есть Нм/с.
При вводе
N
в квт и n в об/мин
к
9650
N
M
n
= Нм.
6.5. Кручение стержней некруглого поперечного
сечения
При кручении стержней некруглого поперечного сечения оказывается
несправедливой гипотеза плоских сечений. Происходит так называемая депланация
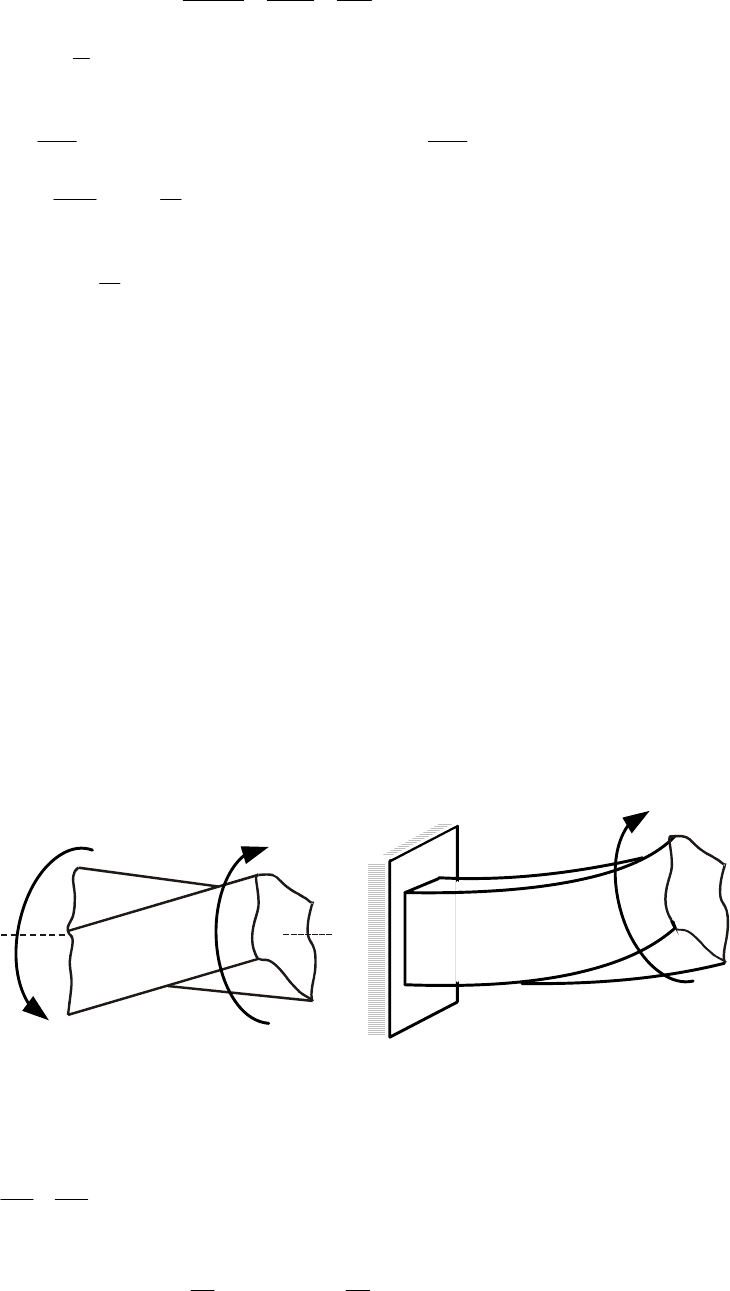
(искривление) сечений (рис. 6.12).
В связи с развитием депланаций различают два вида кручения стержней некруглого
поперечного сечения: свободное и стесненное.
Кручение называется свободным, если депланации всех поперечных сечений
одинаковы по длине стержня. При переменных депланациях кручение называется
стесненным.
При свободном кручении осевые смещения всех точек всех сечений одинаковы,
следовательно, в поперечных сечениях действуют только касательные напряжения ,
а (рис. 6.12, а).
τ
0σ=
При стесненном кручении осевые смещения точек сечений различны, появляется
осевые деформации и, следовательно, в поперечных сечениях действуют и
касательные напряжения , и нормальные напряжения
τ
σ
(рис. 6.12, б).
Приведенные далее в этом разделе расчетные формулы относятся к свободному
кручению стержней.
свободноеѝ кр
у
чение
стесненное
ѝ
кр
у
чение
Рис. 6.12. Депланация прямоугольного сечения при кручении
Точное решение задачи кручения для некоторых типов поперечного сечения дается в
теории упругости. Расчет стержня произвольного поперечного сечения на кручение
сводится к решению уравнения Пуассона (формула 23.5 из раздела 23.6.1).
22
22
20G
zy
∂ϕ ∂ϕ
++θ=
∂∂
где
ϕ
— функция напряжений, связанная с касательными напряжениями
соотношениями
xy
z
∂ϕ
τ=
∂
xz
y
∂
ϕ
τ=−
∂
.
Решение уравнения Пуассона методом конечных элементов рассматривается в
разделе 23.6.3. Такому уравнению подчиняются многие явления природы и техники,
что послужило поводом для проведения аналогий между различными явлениями.
Рассматривая кручение стержней некруглого сечения, можно использовать в
частности мембранную и гидродинамическую аналогии.
В мембранной аналогии касательные напряжения при кручении стержня
пропорциональны углу наклона касательной к резиновой мембране, натянутой на
отверстие, имеющее форму поперечного сечения стержня, и надутой внутренним
давлением.
В гидродинамической аналогии распределение касательных напряжений при
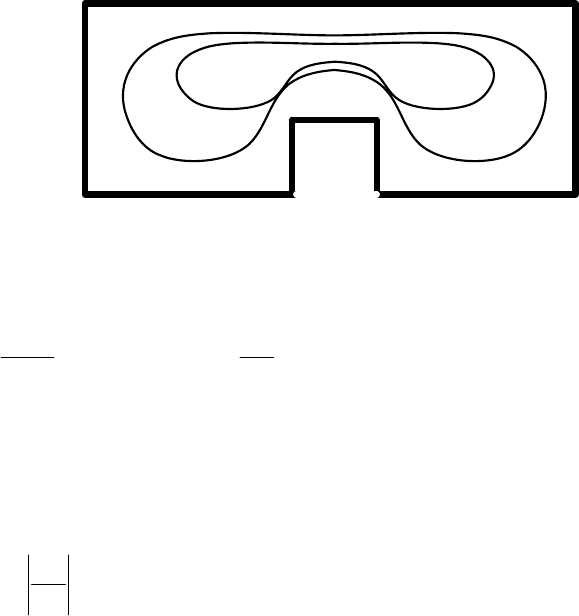
кручении стержня пропорционально распределению скоростей движения жидкости в
бассейне, имеющем форму поперечного сечения стержня (рис. 6.13).
59
Методы аналогий лучше использовать для выбора опасных точек в поперечном
сечении, а не для расчета напряжений. Определять же напряжения и перемещения
лучше всего методом конечных элементов с использованием вычислительных
комплексов.
Рис. 6.13. Движение жидкости в бассейне
Для удобства использования результаты расчета стержней любого поперечного
сечения принято представлять в той же форме, что и для стержней круглого
поперечного сечения, а именно:
к
к
M
l
GJ
ϕ
⋅
=
⋅
к
max
к
W
M
τ
= (6.18),
где
к
J
и — эмпирические или расчетные коэффициенты, называемые
соответственно момент инерции при кручении и момент сопротивления при
кручении. Для стержней круглого или кольцевого сечения
к
W
к
p
J
J
=
и
к
p
WW= . Для
стержней некруглого поперечного сечения чаще всего эти коэффициенты берутся из
справочников.
Условие прочности при кручении
[] [ ]
к
max
к
(0,5 0,6)
W
=≤≈−
M
τ
τσ
к
(6.19).
Приведем, имеющиеся в справочниках формулы для расчета
J
и W для наиболее
часто применяемых форм поперечного сечения.
к
Прямоугольное сечение
На рисунке 6.14 приведены эпюры касательных напряжений по осям симметрии
прямоугольного сечения и по диагонали.
60
