Ляско В.И. Стратегическое планирование развития предприятия

Подождите немного. Документ загружается.

Рыночные

риски

могут

быть вызваны следующими факторами:

• конкурентов больше, чем может выдержать рынок;

• каналы сбыта не

могут

обслуживать все предприятия и фирмы;

• ограниченность ресурсов;

• обманчивый рост рынка (или степени его ненасыщенности);

• покупательские предпочтения (покупатели, например, пред-

почитают импортный товар).

Проведение анализа риска направлено на то, чтобы предоста-

вить потенциальным партнерам необходимые данные для

приня-

тия

решений о целесообразности участия в проекте и предусмот-

реть меры по защите от возможных финансовых потерь.

При

управлении проектами рассмотрение вопросов

учета

иска,

как

правило, осуществляется применительно к основным его

участ-

никам:

заказчику, инвестору и исполнителю или продавцу, инвес-

тору

и покупателю, а также страховой компании.

При

анализе риска любого проекта можно рекомендовать кри-

терии, предложенные известным американским экспертом Б. Бер-

лимером, а именно:

• потери от риска независимы

друг

от

друга;

• потери по одному из направлений «портфеля рисков» не обяза-

тельно увеличивают вероятность потери по

другому

направле-

нию

(за исключением форсмажорных обстоятельств);

• максимально возможный

ущерб

не должен превышать

финан-

совых возможностей участника.

14.3. Методы определения величины

(степени) риска

Риск

— категория вероятностная. Поэтому его измеряют как

вероятность определенного уровня потерь, и каждый предприни-

матель или каждое предприятие устанавливает для себя приемле-

мую степень риска.

Для определения степени риска используют статистические,

экспертные,

комбинированные методы, а также математическое

программирование и теоретико-игровые методы.

261

Статистические методы основаны на сборе, обработке и анали-

зе статистических материалов и включают в себя методы последо-

вательного анализа и статистических испытаний.

Суть статистического метода заключается в том, что изучается

статистика потерь и прибылей, имеющих место в данном (или ана-

логичном) производстве, устанавливается величина и частота по-

лучения той или иной экономической отдачи, и на этой основе

составляется наиболее вероятный прогноз на

будущее.

Под

«отда-

чей»

понимается экономическая рентабельность (или эффектив-

ность затрат), которая рассчитывается как отношение прибыли

затратам (или инвестициям), необходимым для получения этой

прибыли.

Экспертный метод м©жет быть реализован путем обработки

мнения

опытных предпринимателей или специалистов. Желатель-

но,

чтобы эксперты сопровождали свои оценки данными о вероят-

ности возникновения различных значений потерь в натуральном

или

относительном измерении.

Поскольку при подборе группы экспертов очень трудно пред-

ставить их как группу

«идеальных»

экспертов, т.е. способных ин-

туитивно делать абсолютно верные заключения, обладающих не-

зависимостью суждений и умеющих оценивать проблему с различ-

ных точек зрения, то при оценке риска этим методом можно

ограничиться значениями вероятности допустимого и критиче-

ского риска, полученными по экспертным оценкам, или же просто

оценить сумму наиболее вероятных потерь.

Наиболее часто используемым в практике является метод, осно-

ванный

на совместном использовании статистического и эксперт-

ного способа оценки риска. Этот метод получил название комби-

наторного.

Математическое программирование подразделяется на ли-

нейное,

нелинейное, динамическое, а также сотовое планиро-

вание.

Линейное и нелинейное — отличаются функциями. Динамиче-

ское программирование служит для выбора наилучшего плана

выполнения

многоэтапных действий, когда результат каждого

последующего этапа зависит от предыдущего.

262

Сотовое планирование предназначено для составления рацио-

нального плана ведения действий, предусматривающего решение

задачи в кратчайший срок с наилучшими результатами.

Теоретико-игровые методы предназначены для обоснования

решений в условиях неопределенности, неполноты информации.

позиций математического программирования выбор наилуч-

шего (оптимального) решения в самом общем виде можно предста-

вить как отыскание максимума (минимума) целевой функции:

W = f(a

,...,

а; Ь,,

,...,

b; x,,

,...,

\),

где а — заданные параметры, например количество и качество

ресурсов;

b — управляемые параметры;

— неизвестные, неуправляемые параметры (погода и т.д.).

Задача выбора наилучшего решения может быть сформули-

рована следующим образом: найти такие значения управляемых

параметров..., которые при заданных параметрах... с

учетом

неиз-

вестных параметров ... обеспечивают получение max (min) целе-

вой функции...

Наличие неизвестных (неуправляемых) параметров ставит воп-

рос о принятии решения в условиях неопределенности, т.е. неизве-

стности состояния неуправляемых параметров. Конечно, задав-

шись тем или иным значением неизвестных параметров, можно

рассчитать значение..., но

тогда

получаем набор возможных опти-

мальных значений, и задача

будет

сведена к решимости выбора из

множества одного лучшего. Принятие такого решения связано

с неизбежным риском.

Необходимо, конечно, сделать все, чтобы свести возможный

риск

к минимуму, но, как правило, в реальной жизни принятие ре-

шений,

сопряженных с риском, оказывается неизбежным, и нужно

научиться расчетливо рисковать, т.е. овладеть искусством риска.

Существует

разумный, обоснованный риск, который признает-

ся

неотъемлемой частью искусства руководителя.

Существует

и риск необоснованный, безрассудный, присущий

авантюрным действиям.

263

Итак,

«риск»

представляет из себя совокупность:

1) характера действий в неясной, неопределенной обстановке

(наудачу);

2) потребности рисковать, когда возможен

успех

(вероятность

больше);

3) ожидаемый результат носит случайный характер (случай-

ный

исход).

Во всех случаях риск — это действие наудачу в надежде на

счастливый исход. Идти на риск вынуждает неопределенность,

неясность обстановки, т.е. такая ситуация, когда необходимо дейст-

вовать, а как — неизвестно. Причем чем больше неопределенность

при

принятии решений, тем больше и риск.

Основные причины неопределенности:

° незнание;

° случайность;

° противодействие (некто злонамеренно путает наши карты, ме-

шает нашим начинаниям).

Для определения величины риска используем следующий под-

ход. Представим ситуацию, в которой требуется отгадать, как упа-

дет монета: кверху «решкой» или «орлом». Падение монеты той

или

иной стороной — явление случайное. Вместе с тем в этом слу-

чайном явлении просматривается определенная закономерность:

интуиция подсказывает, что в половине всех случаев наш прогноз

подтвердится.

Число,

характеризующее степень возможности появления слу-

чайного события, называется вероятностью.

Таким

образом, вероятность появления «решки» или «

орла»

равна

составляет половину (0,5 или 50%). А мерой риска

будет

вероят-

ность ошибиться при названии той или иной стороны монеты.

Для определения вероятности риска необходимо вычесть веро-

ятность выхода предсказанного события из вероятности появле-

ния

любого возможного события, т.о. в нашей ситуации:

риска = 1 - 0,5 - 0,5 или 50%,

т.е. из 100 предсказаний риск ошибиться — в среднем 50%.

264

Сложнее обстоит дело, если представить ситуацию, в которой

монета

упадет

«орлом»

кверху два раза подряд. В этом

случае

пер-

вое появление

«орла»

соответствует половине всех возможных

шансов,

повторное — также половине, но уже тех шансов, которые

благоприятствовали этому появлению. Речь, следовательно, идет

уже о 50% от половины, т.е. о вероятности, равной 0,25 или 25%.

В этой ситуации значение риска определяется следующим обра-

зом:

риск = 1,0 - 0,25 = 0,75 или 75%.

Следует отметить, что риск в этой ситуации вырос не в два,

а только в полтора раза. Продолжая аналогичные расчеты, можно

установить, что риск предсказания появления

«орла»

в различных

ситуациях составит следующие значения:

° три раза подряд — 87,5%;

° четыре раза подряд — 93,8%;

° пять раз подряд — 96,9% и т.д.

Анализ показывает, что основное нарастание степени риска

происходит уже при предсказании первых повторений выпадения

«орла».

Так, при переходе от предсказания однократного появле-

ния

«орла»

к двухкратному риск ошибки увеличивается в 1,5 раза,

а при переходе от четырехкратного к пятикратному его появле-

нию

риск возрастает всего на 3%.

В практической деятельности, как правило, интересуются не

появлением какого-либо события определенное число раз, а тем,

что такое событие может случиться не менее определенного числа

раз.

Например, каков риск предсказания, что монета

уиадет

не ме-

нее одного раза (т.е. хотя бы один раз)

«орлом»

вверх при четырех

подбрасываниях? Очевидно, риск этот

будет

меньше, чем при уга-

дывании точного числа появления цифры. Для ответа на этот во-

прос обратимся к табл. 14.2.

Величина риска предсказания появления

«орла»

не менее опре-

деленного числа раз при нескольких подбрасываниях монеты (в %).

Из

табл. 14.2 видно, что риск предсказывания выпадения

«орла»

хотя бы один ра'з уже при четырех подбрасываниях доста-

точно невелик (равен 6,2%).

265

Таблица

14.2

Предсказанное

количество

появлений

«орла»

Количество

подбрасываний монеты

100

12,5

87,5

100

6,2

31,2

68,8

93,8

100

ЗД

18,8

81,2

96,9

Оценка

возможного риска полезна при принятии любого реше-

нии.

Так,

примеру, перед предпринимателем стоит задача оценки

риска

при

пяти некоторых событиях, которые

равной степени

могут

как

произойти,

так и нет

(завоевание большей доли рынка,

потеря

на

рынке определенной

его

доли, потеря прибыли

т.п.).

Риск

предсказания того,

что

произойдет

не

менее

трех

из

этих

со-

бытий, невелик (50%). Еще

большей уверенностью можно

ожи-

дать

не

менее

двух

событий (риск равен 18,8%),

а уж

одно-то прои-

зойдет наверняка (риск ничтожен

равен

3,1%).

Предприниматель должен своевременно оценить степень риска

при

производстве

той или

иной сделки

или

при подписании конт-

ракта.

расчетах

для

надежности принимается,

что для

обеспече-

ния

своевременности поставок может быть одновременно задейство-

ван не один,

несколько равноценных

независимо действующих

поставщиков. Причем заключение сделки

хотя

бы с

одним

из

этих

поставщиков достаточно

для

обеспечения потребностей

постав-

ках. Опытным

путем

может быть определена эффективность

каж-

дого

поставщика

—

вероятность поставки

установленные сроки

должном объеме. Поскольку, однако,

нет

гарантии,

что

такая

поставка произойдет, возникает риск

ее

срыва. Причем, естествен-

но,

чем

больше поставщиков задействовано

и чем

выше вероят-

ность поставок каждого

из

них,

тем

риск меньше.

Эту

зависимость

266

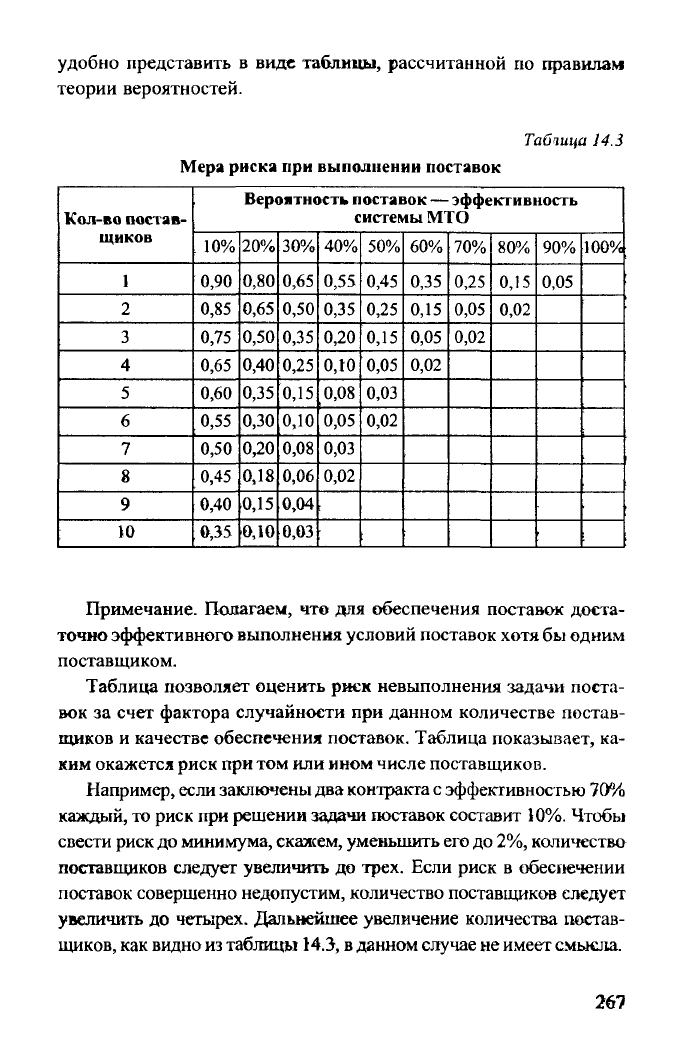
удобно представить в виде таблицы, рассчитанной по правилам

теории вероятностей.

Табчица

14.3

Мера риска

Кол-во постав-

щиков

при выполнении поставок

Вероятность поставок

—

эффективность

системы МТО

10%

0,90

0,85

0,75

0,65

0,60

0,55

0,50

0,45

0,40

0,35

20%

0,80

0,50

0,40

0,35

0,30

0,20

0,18

0,15

0,10

30%

0,65

0,35

0,25

0,15

0,10

0,08

0,06

0,04

0,03

40%

0,55

035

0,20

0,10

0,08

0,05

0,03

0,02

50%

0,45

0?5

0,15

0,05

0,03

0,02

60%

0,35

015

0,05

0,02

70%

0,25

0,02

80%

0,15

90%

0,05

100%

Примечание.

Полагаем, что для обеспечения поставок доста-

точно эффективного выполнения условий поставок

хотя

бы одним

поставщиком.

Таблица позволяет оценить риск невыполнения задачи поста-

вок

за

счет

фактора случайности при данном количестве постав-

щиков

и качестве обеспечения поставок. Таблица показывает, ка-

ким

окажется риск при том или ином числе поставщиков.

Например,

если заключены два контракта с эффективностью 70%

каждый, то риск при решении задачи поставок составит 10%. Чтобы

свести риск до минимума, скажем, уменьшить его до 2%, количество

поставщиков

следует

увеличить до

трех.

Если риск в обеспечении

поставок совершенно недопустим, количество поставщиков

следует

увеличить до

четырех.

Дальнейшее увеличение количества постав-

щиков,

как видно из таблицы 14.3, в данном

случае

не имеет смысла.

26?

14.4. Методы оценки финансового риска

Риск

в хозяйственной и коммерческой деятельности

всегда

по-

рождает вероятность возникновения денежных потерь, вытекаю-

щую из особенностей операций.

Коммерческие риски бывают

«чистые»

и «спекулятивные».

«Чистые»

риски — это возможность получения убытка или ну-

левого

результата.

«Спекулятивные» риски — это возможность

получения как положительного, так и отрицательного

результата.

Эти риски получили название «финансовые риски».

Финансовый

риск имеет математически выраженную вероят-

ность наступления потери, которая опирается на статистические

данные и может быть рассчитана с достаточно высокой точностью.

Чтобы количественно определить величину финансового рис-

ка,

необходимо знать все возможные последствия какого-нибудь

отдельного действия и вероятность самих последствий. Поскольку

вероятность означает возможность получения определенного ре-

зультата,

то применительно к экономическим задачам методы тео-

рии

вероятности сводятся к определению значений вероятности

наступления событий и к выбору из возможных событий самого

предпочтительног о исходя из наибольшей величины математиче-

ского ожидания. Иначе говоря, математическое ожидание какого-

либо события равно абсолютной величине этого события, умно-

женной

на вероятность его наступления.

примеру, имеются два варианта вложения капитала. Установ-

лено,

что при вложении капитала в мероприятие А1 возможно по-

лучение прибыли в

сумме

15 млн руб. с вероятностью 0,6, а при

вложении капитала в мероприятие А2 сумма прибыли составит

20 млн руб., но с вероятностью 0,4. Тогда ожидаемое получение

прибыли (т.е. математическое ожидание) составит по мероприя-

тию А1 = 15 х 0,6 = 9 млн руб., А2 = 20 х 0,4 = 8 млн руб.

Таким

образом, наиболее предпочтительно вложение капитала

мероприятие А1.

Вероятность наступления события может быть определена

объективным или субъективным методами.

268

Объективный метод определения вероятности основан на вы-

числении частоты, с которой происходит данное событие.

Напри-

мер,

если известно, что при вложении капитала в какое-либо меро-

приятие прибыль в

сумме

15 млн руб. была получена в 120

случаях

из

200, то вероятность получения такой прибыли составляет:

Р=

120/200

= 0,6.

В субъективном методе используются субъективные критерии,

которые основываются на различных предположениях. К таким пред-

положениям

могут

относиться суждение оценивающего, его личный

опыт, оценка эксперта, мнение финансового консультанта и т.п.

Величина (степень) риска измеряется

двумя

критериями:

1) среднее ожидаемое значение;

2) колеблемость (изменчивость) возможного

результата.

Среднее ожидаемое значение — это знание такой величины собы-

тия,

которая связана с неопределенной ситуацией. Это средневзвешен-

ная

величина, где вероятность величин каждого

результата

использует-

ся

в качестве частоты или веса соответствующего значения. Среднее

ожидаемое значение измеряет ожидаемый в среднем

результат.

примеру, если известно, что при вложении капитала в меро-

приятие А из 120

случаев

прибыль в размере 1 млн руб. была получе-

на

в 48

случаях

(р = 0,4), прибыль в 2 млн руб. в — 42

случаях

(р =

0,35) и прибыль в 0,8 млн руб. — в 30

случаях

(р =

0,25),

то среднее

ожидаемое значение выразится в следующей сумме:

S = 1 х 0,4 + 2 х 0,35 + 0,8 х 0,25 = 1,3 млн руб.

Допустим также, что при вложении капитала в мероприятие А2

средняя прибыль составила:

S = 1,5 х 0,3 + 2 х 0,5 + 1,6 х 0,2 = 1,77 млн руб.

Сравнивая

две суммы ожидаемой прибыли при вложении капита-

ла в мероприятия, можно сделать вывод, что при вложении в меро-

приятие А1 величина ожидаемой прибыли колеблется от 0,8 до

2 млн руб., и средняя величина составляет 1,3 млн руб. При вложе-

нии

капитала в мероприятие А2 величина получаемой прибьши колеб-

лется от 1,5 до 2,0 млн руб., и средняя величина составляет 1,77 млн руб.

269

Средняя

величина представляет собой обобщенную количест-

венную характеристику и не позволяет принять решение в пользу

какого-либо варианта вложения капитала без определения меры

изменчивости

возможного результата, т.е. без определения дис-

персии

и среднего квадратического отклонения.

Дисперсия

— это среднее взвешенное из квадратов отклонений

действительных результатов от средних ожидаемых.

Среднее квадратическое отклонение является именованной ве-

личиной

и указывается в тех же единицах, в каких измеряется

варьирующий признак.

Дисперсия

и среднее квадратическое отклонение

служат

мера-

ми

абсолютной колеблемости, для анализа же обычно используют

коэффициент

вариации, т.е. отношение среднего квадратического

отклонения

к средней арифметической.

Коэффициент

вариации изменяется от 0 до 100%. В экономиче-

ской

статистике установлена следующая оценка этого

коэффициента:

• до 10% — слабая колеблемость;

• 10-25% — умеренная колеблемость;

• свыше 25% — высокая колеблемость.

Управление риском

Каждый

участник любого проекта, сделки, контракта заинтере-

сован

в том, чтобы исключить возможность неудачи при реализа-

ции

решения или хотя бы свести к минимуму убытки.

Бедственно,

что полной уверенности в благополучном исходе

ни

KOI

о быть не может, потому фактор риска

существует

и при-

знается

всеми. Теория и практика разработали достаточное коли-

чество средств и путей, способствующих снижению потерь от воз-

можных просчетов и провалов при участии в различных проектах.

Управление проектом должно осуществляться с обязательным

учетом риска участия в нем. Так как последствия неучтенного рис-

ка

(даже неучет риска возможности частичных неудач проекта)

могут

обернуться перерасходом времени и средств на его выпол-

нение,

а для крупных проектов, как правило, почти всегда увеличе-

нием

прямых финансовых затрат и дополнительного времени для

завершения

работ, то готовность идти на риск в немалой степени

270