Лунин Л.С., Благин А.В., Баранник А.А. Лекции по физике. Часть I. Механика, молекулярная физика и термодинамика

Подождите немного. Документ загружается.

161

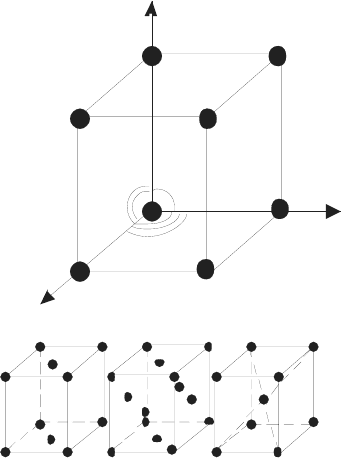
ленная ячейка, не имеющая дополнительных узлов кроме вершин ни

внутри, ни на гранях и ребрах, называется примитивной или Р-ячейкой.

Как правило, целесообразно в качестве элементарной выбирать не прими-

тивную, а сложную ячейку с дополнительными атомами – узлами (распо-

ложение атомов в решетке называется узлом): в центре оснований

(базоцентрированная) или граней (бокоцентрированная) – С-ячейка; в цен-

тре всех 6 граней (гранецентрированная) – F-ячейка; на пересечении внут-

ренних диагоналей (объемно-центрированная) – I-ячейка.

Рис. 14.1

Условия выбора ячеек: ячейка должна содержать все элементы сим-

метрии, присущие данному веществу; число равных сторон и прямых уг-

лов должно быть максимальным; при этом объем ячейки должен быть ми-

нимальным.

Оказалось, что все многообразие существующих кристаллических

структур может быть описано с помощью 14 типов трансляционных реше-

ток (показано математически в 1848г.), называемых решетками О. Бравэ

(1811–1863), распределенных по семи кристаллографическим системам

или

сингониям (табл. 14.1).

162

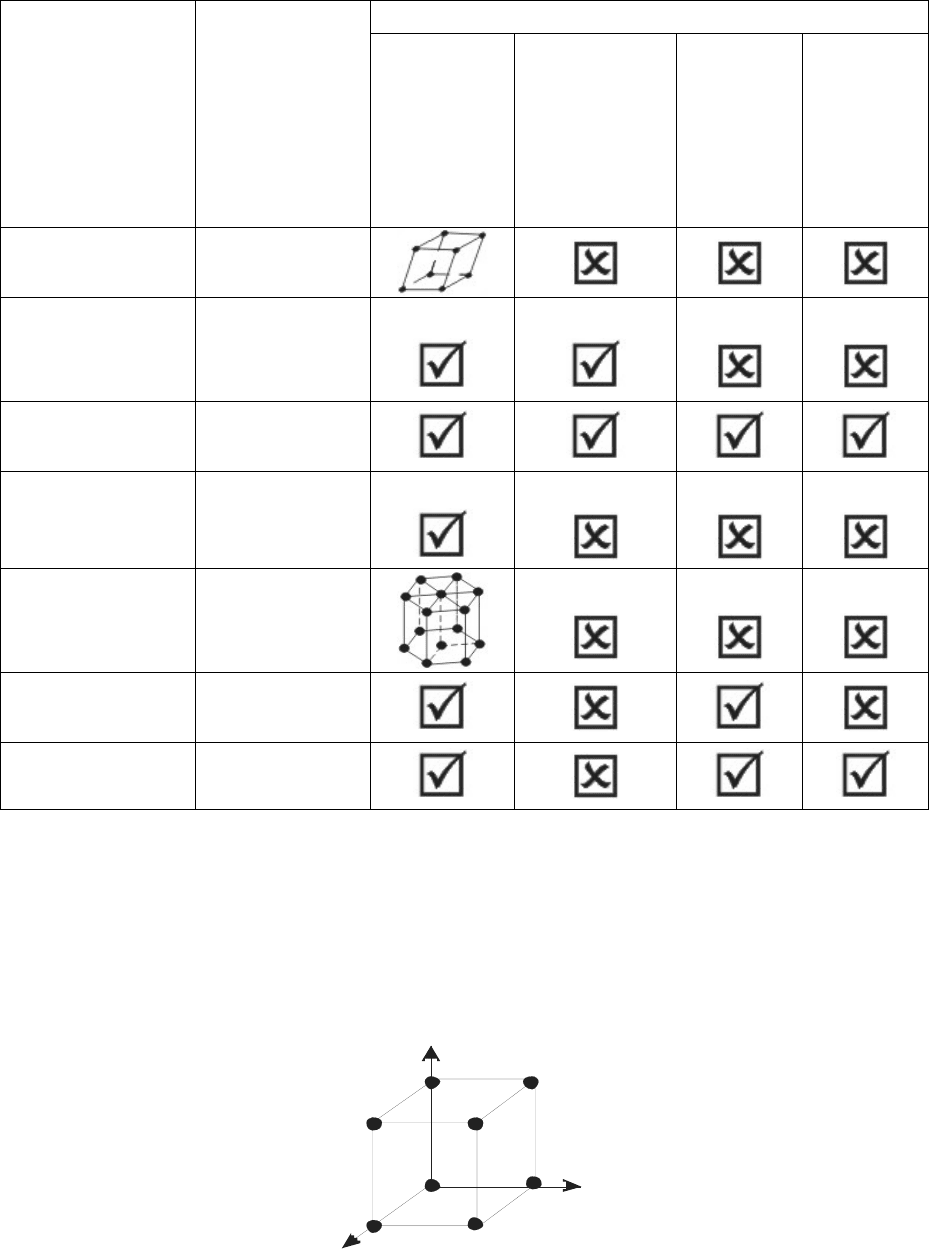
Таблица 14.1

Ячейки

Сингония

Параметры

ячейки

Прими-

тивная

(Р-ячейка)

Базоцен-

трирован-

ная

(С-ячейка)

Объем-

ноцен-

триро-

ванная

(I-ячейка)

Гране-

центри-

рован-

ная

(F-

ячейка)

Триклинная

≠

α≠β≠γ

Моноклинная

≠

=90°,

≠90°

Ромбическая

≠

=90°

Тригональная

(ромбоэдри-

ческая)

a=b=c,

γ≠

90°

Гексагональ-

ная

a=b

≠

=90°,

=60°

Тетрагональ-

ная

a=b

≠

=90°

Кубическая

a=b=c,

=90°

Следует отметить, что обычно под

кристаллической решеткой по-

нимают физическую реальность, а под

кристаллической структурой –

(математическую) абстракцию. Месторасположение атомов в узлах струк-

туры обозначают с помощью целых чисел – кристаллографических

индек-

ов Миллера (англ. У. Миллер (1801–1880)), например, [[110]] (рис. 14.2).

Рис. 14.2

163

Эти индексы связаны с длиной отрезков, отсекаемых соответствую-

щей плоскостью на трёх осях кристаллографической системы координат.

Длины отрезков, отсекаемых любой атомной плоскостью кристалла на

осях координат, выраженные в постоянных решётки а, b, с, всегда являют-

ся целыми числами S

, S

. Если обратные им величины привести к об-

щему знаменателю, а затем отбросить его, то полученные 3 целых числа

h=S

, k=S

, l=S

и есть индексы Миллера. Впрочем, иногда для до-

полнительных узлов в сложных ячейках используют обозначения [1/2 1/2 0] и

т.д. Обозначения прямых записываются в одинарных скобках [hkl], а плос-

костей – в круглых скобках. Например, [110] обозначают прямую, прохо-

дящую через начало координат [[000]] и узел [[110]], а (110) обозначают

плоскость, перпендикулярную направлению [110]. Отрицательные индек-

сы

)011(

−−

(минус 1, минус 1, нуль) обозначают плоскость, пересекающую-

ся с отрицательным направлением













−−

011 осей координат. Совокупности

плоскостей, симметрично равных друг другу, записывают в фигурных

скобках {h k l}.

Помимо кристаллографии, индексы Миллера используются также в

рентгенографии, электронографии и нейтронографии для обозначения

пучков, рассеянных соответствующими атомными плоскостями кристалла.

В реальных кристаллах, в отличие от идеальных, как правило, на-

блюдаются

дефекты структуры. Под дефектами понимают всякое откло-

нение от идеального строения кристалла. Дефекты подразделяются на:

–

точечные – протяженность не более межатомного размера в лю-

бую сторону: чужеродные атомы в узлах и междоузлиях (примесь), отсут-

ствие собственных атомов в узлах решетки (вакансия);

–

линейные – протяженность в одном из направлений больше меж-

атомного, в двух остальных порядка межатомного: краевые, винтовые и

смешанные (нарушение правильного чередования атомных плоскостей),

микротрещины;

–

двухмерные – границы зерен и двойников, межфазные границы,

стенки доменов, поверхность любого кристалла;

–

объемные – пустоты, включения иной фазы (в процессе кристал-

лизации).

Остановимся подробнее на дислокациях, так как механические свой-

ства ТТ во многом определяются наличием и плотностью N

– их числом на

единицу площади. В наиболее совершенных монокристаллах N

∼10

-10

см

-2

в сильно деформированных кристаллах N

∼10

-10

см

-2

Краевой дислокацией (рис. 14.3) называется отсутствие полу-

плоскости в кристалле (или лишняя полуплоскость)

. Линия, отделяю-

щая дефектную область кристалла от «нормальной», называется линией

164

дислокации (OO

на рис.(14.3), стрелкой указано направление сдвиговой

деформации).

Рис. 14.3

Признаком краевой дислокации является условие ОО'⊥

. Для вин-

товой

дислокации ОО'||

(рис. 14.4), для смешанной дислокации в одних

точках ОО'⊥

, а в других ОО'||

(рис.14.5).

В настоящее время считается, что

границы зерен (кристаллитов)

представляют собой стенки из дислокаций (рис. 14.6).

Рис. 14.4 Рис. 14.5 Рис. 14.6

ТТ можно классифицировать и по ряду различных признаков. Ино-

гда основой классификации ТТ является характер межатомных сил. Со-

гласно этой классификации все ТТ подразделяют на металлические, кова-

лентные, ионные и молекулярные кристаллы. ТТ можно классифицировать

и по электропроводности: полупроводники, проводники (металлы) и ди-

электрики, а также по типу ячейки Бравэ, по прочности и т.д.

14.2. Механические свойства ТТ. Коэффициент термического

расширения (КТР)

Под механическими свойствами ТТ понимают их механическую ре-

акцию (деформация) на

внешнее воздействие: растяжение–сжатие, из-

гиб, кручение, удар

и т.п. В результате внешнего силового воздействия в

ТТ

появляются напряженные состояния. Обычно оно появляется под

действием поверхностных сил

, действующих на выделенный элемент

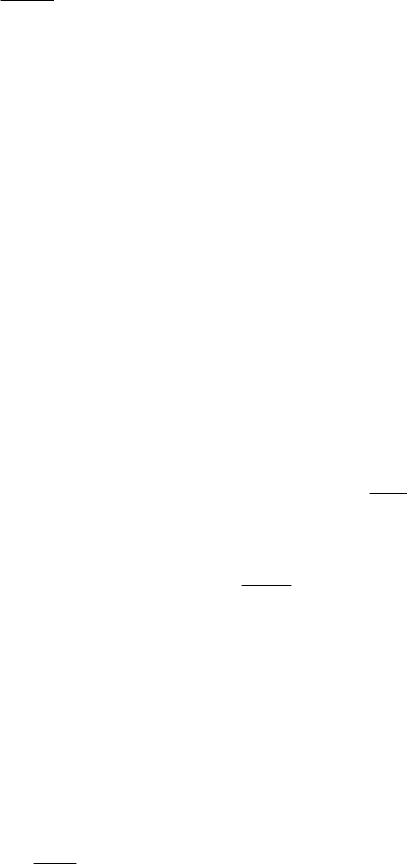
165

площади поверхности со стороны других тел, например, реакция опоры.

Объемные силы, например, сила тяжести деформации, обычно деформа-

ций и

напряженных состояний не вызывают.

Отношение модуля поверхностной силы dF к площади воздействия

dS называется

напряжением:

. (14.1)

Различают истинные и условные напряжения. Для определения ис-

тинного напряжения необходимо учитывать изменение площади воздейст-

вия и, следовательно, приложенной внешней поверхностной силы. В об-

щем случае напряженное состояние ТТ описывают с помощью тензора

(матрицы) напряжений

для учета анизотропности кристаллов (при этом

учитываются элементы симметрии и различия механических свойств вдоль

разных направлений).

Под действием напряжений ТТ может изменять свою форму, либо

объем, но, как правило, и то, и другое меняется одновременно – ТТ дефор-

мируется.

Основными видами деформации являются растяжение–

сжатие и сдвиг

, все остальные случаи могут быть получены посредством

их комбинаций. Количественной мерой деформации является в простей-

шем случае так называемая

относительная деформация

∆

или

относительное поперечное растяжение (сжатие)

∆

, где l – длина

стержня, d – его диаметр, ∆

l – абсолютное удлинение (абсолютная де-

формация

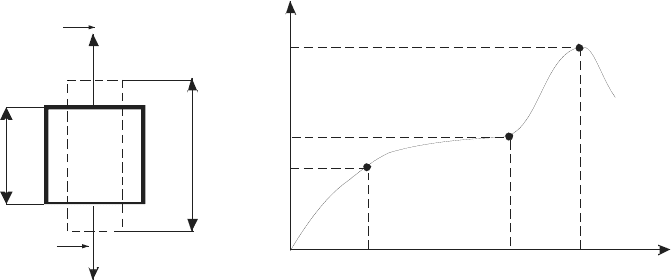
Экспериментально установлено, что, как правило, при деформации в

одном направлении тело деформируется и в других направлениях (рис. 14.7).

Поэтому величины

взаимосвязаны соотношением

−=

, (14.2)

где

– коэффициент Пуассона, зависящий от природы (свойств) мате-

риала.

166

l+ l∆

пр

Рис. 14.7 Рис. 14.8

Общий вид зависимости

(

) напряжения от величины деформации

представлен на рис. 14.8. В зависимости от природы тел вид участков

кривой различается углами наклона и протяженностью. Участок 01 –

об-

ласть упругой деформации

: тело при снятии внешнего воздействия прак-

тически полностью восстанавливает свою форму и объем. Наибольшее

значение

, соответствующее этому, называется пределом упругости.

При дальнейшем (

) незначительном росте напряжений вплоть до не-

которого значения

– предела текучести – деформация значительно

увеличивается (

область пластических деформаций – тело не восстанав-

ливает свои размеры и форму). Пластические деформации не приводят к

нарушению сплошности тела. Следует отметить интересное явление: если

тело подвергнуть пластической деформации, а затем, сняв нагрузку, соз-

дать напряжение еще раз, то предел упругости увеличится. Это явление на-

зывается

деформационным упрочнением. Если участок 12 значителен, то

материал называют

вязким, если мал – хрупким. Дальнейшее увеличение

напряжений при значениях больших

предела прочности

пр

вызывает

необратимое разрушение тела.

В достаточно узкой области, в которой величина деформации про-

порциональна приложенному напряжению вплоть до некоторого значения

напряжения, называемого пределом пропорциональности,

выполняется

(1660г.) закон Р. Гука (1635–1703):

в случае деформации растяжения–сжатия

, (14.3)

где Е – модуль (1807г.) Т. Юнга (1773–1829) – численно равен напряже-

нию, требуемому для единичного удлинения стержня из данного материала;

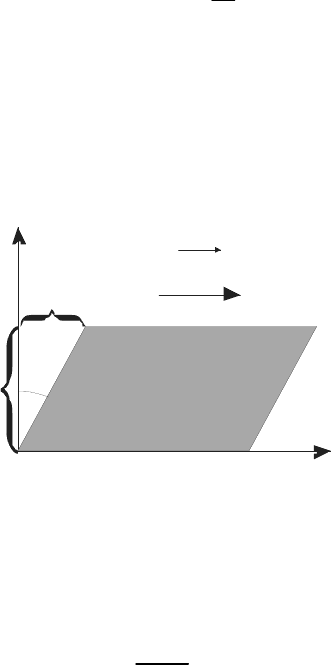
в случае сдвиговой деформации (рис.14.9)

167

γατ

GGtg ===

, (14.4)

где

– касательное напряжение;

G – модуль вектора сдвига;

– угол сдвига;

– относительный сдвиг;

Рис. 14.9

- в случае объемной деформации

Ω=

∆

χχ

, (14.5)

где P – давление, напряжение всестороннего сжатия;

Ω – относительная объемная деформация;

– модуль всестороннего сжатия.

Формулы (14.3)–(14.5) называются элементарными формами за-

писи закона Гука для изотропных ТТ

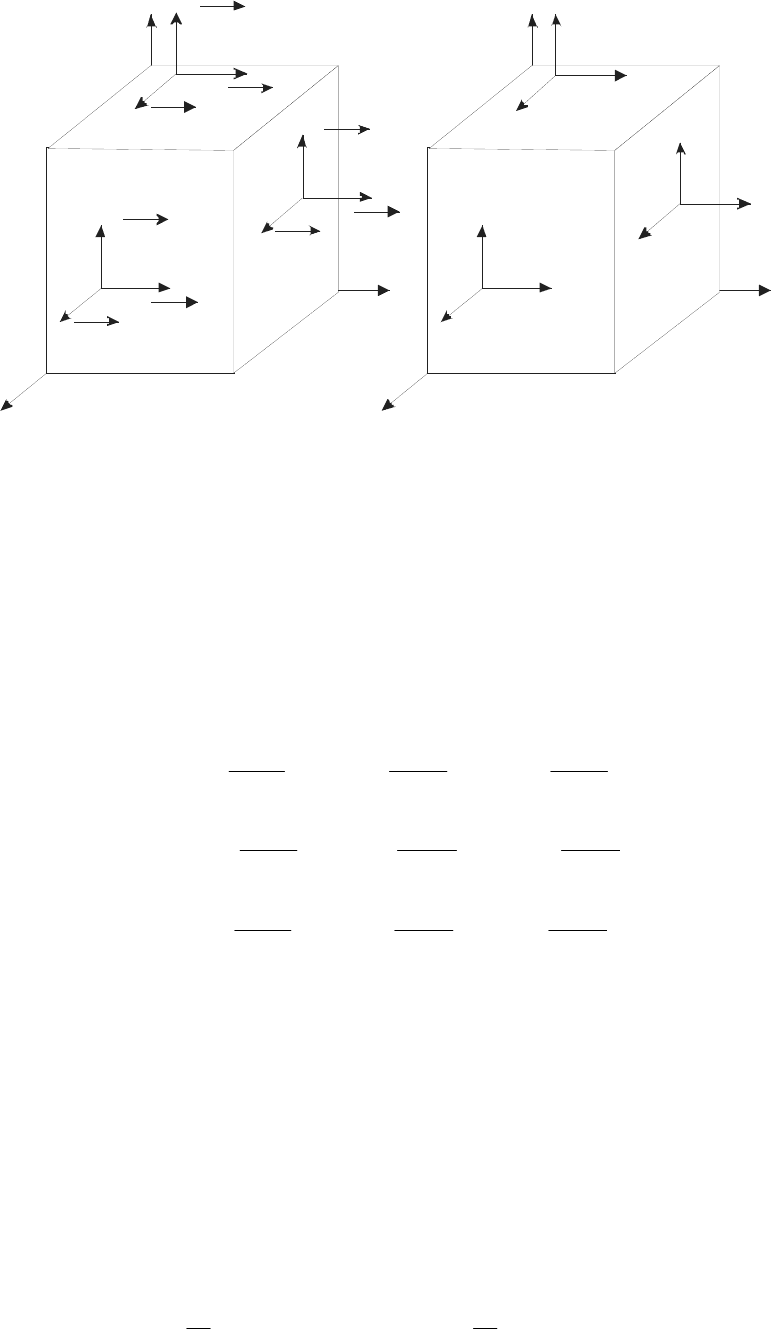
Выделим бесконечно малый объем вещества в виде куба (рис. 14.10).

Если на ТТ действуют силы, то в отличие от жидкости и газа эти силы

ориентированы произвольно. Обозначим направление Ох за 1, Оy – за 2, Oz

– за 3.

Если вещество находится в статическом равновесии, то:

силы, действующие на противоположные грани куба, равны по

модулю и противоположны по направлению;

полный момент всех сил, действующих на куб, равен нулю, т.е.

достаточно рассмотреть силы, приложенные к трем граням с одной общей

вершиной, например, к граням, обращенным на рис. 14.10 к зрителю.

168

а) б)

Рис. 14.10

На рис. 14.10, а указаны компоненты, действующих сил. Например,

сила

→

dF – это составляющая силы

→

dF , приложенная в направлении 1

(Ох). Относя обозначенные составляющие к площади грани dS и проецируя

полученные векторы на оси координат, получаем:

xzxyx

2111

; ; ===

ττσ

;

yzyyx

2212

; ; ===

τστ

; (14.6)

zzyzx

332313

; ; ===

σττ

Величины, определяемые по формуле (14.6), называются механиче-

скими напряжениями (см. (14.3) и (14.4)), они полностью характеризуют

силы, приложенные к ТТ и образуют так называемые тензор второго ранга

(матрицу) –

тензор напряжений, где dF

=dF

(см. условия статического

равновесия).

Элементарные законы Гука не учитывают явления (14.2) и (14.6), что

учитывается

νε

для трех направлений в обобщенном законе Гука:

- для удлинения изотропных ТТ:

()

[]

(

)

[

]

zyxx

σνσσσνσεε

+−=+−==

33221111

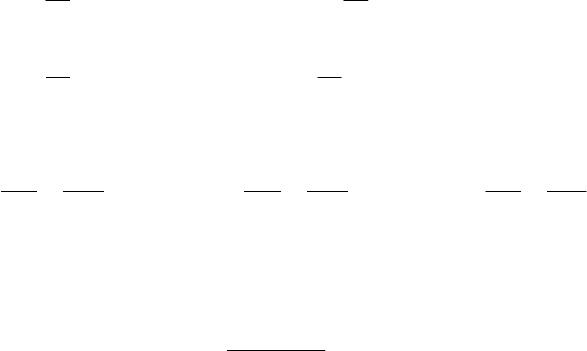
169

()

[]

()

[

]

zxyy

σσνσσσνσεε

+−=+−==

33112222

, (14.7)

(

)

[]

(

)

[

]

yxzyxz

σσνσσσνσεε

+−=+−==

3333

- для сдвигов

εε

===

εε

===

εε

===

Все константы связаны между собой соотношением

)1(2

. (14.8)

Закон Гука для анизотропных (практически всех реальных) ТТ имеет

вид (14.3), но все входящие в него величины являются тензорами (матрицами).

Атомы в кристалле могут совершать колебания в узлах кристалличе-

ской решетки (около) положения равновесия. При сообщении им энергии,

например, при разогреве тела, амплитуда колебаний атомов возрастает. В

квантовой теории показано, что при температуре выше некоторой критиче-

ской колебания атомов в узлах решетки становятся ангармоническими (не-

гармоническими – отклонение в одну сторону больше, чем в другую). Ли-

нейные размеры тела увеличиваются, в связи с этим говорят о тепловом рас-

ширении тел и его характеристике – коэффициенте теплового расширения

(КТР). Материалы соприкасающихся деталей, покрытий должны иметь оди-

наковые или близкие КТР во избежание разрушения изделий и конструкций.

170

ЛЕКЦИЯ 15. ТЕПЛОЕМКОСТЬ И ФАЗОВЫЕ ПЕРЕХОДЫ

1. Классическая теория теплоемкости вещества, границы ее

применимости.

2. Фаза. Метастабильные состояния. Диаграммы состояния.

Тройные точки. Фазовые переходы (ФП) I и II рода. Явление сверхте-

кучести (ФП II рода).

15.1. Классическая теория теплоемкости вещества,

границы ее применимости

(перед изучением данного вопроса следует ознакомиться с

лекцией

11, вопросы 1 и 2)

Простейшей моделью кристалла (ТТ) является правильная (без де-

фектов) кристаллическая решетка, в узлах которой располагаются атомы –

материальные точки, совершающие колебания около положения равнове-

сия. Если колебания малы, то их можно считать гармоническими (проис-

ходящими по закону синуса или косинуса

(

)

sin

tAx ). Так как

средняя кинетическая энергия гармонических колебаний примерно равна

потенциальной энергии, то на каждую колебательную степень свободы в

среднем приходится энергия

kTkT =⋅

2 . Каждый атом обладает тремя

степенями свободы, поэтому его средняя энергия

3kT. Тогда внутренняя

энергия 1 моля ТТ будет

RTkTNU

⋅

, откуда молярная теплоем-

кость ТТ равна

3== . (15.1)

Формула (15.1) выражает эмпирически установленный в 1819г. за-

кон Дюлонга–Пти

(П.Л.Дюлонг (1785–1838), А.Т.Пти (1791–1820)).

Для применимости теоремы о равномерном распределении энергии

по степеням свободы не имеет значения, сколько атомов содержится в мо-

лекуле, т.е., если на один атом в среднем приходится энергия

3kT, то на n-

атомную молекулу придется в среднем

3nkT=3nRT, откуда молярная теп-

лоемкость соединения равна сумме молярных теплоемкостей элементов, из

которых оно состоит:

nRС

. (15.2)

Формула (15.2) – эмпирически установленное в

1864 г. правило

Джоуля–Коппа

, хотя иногда его называют правилом Неймана–Коппа

(1844 г. Д.П.Джоуль (1818–1889), 1864г. Г.Ф.М. Копп (1817–1892), Ф.Э.

Нейман (1798–1895)). Формулы (15.1) и (15.2) ограниченно справедливы.