Лукоянычев В.Г. Электротехника
Подождите немного. Документ загружается.

41
Решая это уравнение относительно угловой частоты ω, величину которой для этого
случая обозначим
0
ω
, находим:
LC
1
0
=
ω
. Так как ,2
00
f
π
ω
=
то .
2
1
0
LC
f
π
=
Соотношение между
L,C и
0
f является условием резонанса напряжений. В этом
случае ток, определяющийся одним лишь активным сопротивлением, может достичь при
незначительности последнего очень большой величины. Одновременно напряжения
IωL и
C
I
ω
на индуктивности и конденсаторе могут стать весьма значительными и превысить
приложенное ко всей цепи напряжение
U. Частоты
0
ω
и
0
f называются резонансными
частотами.
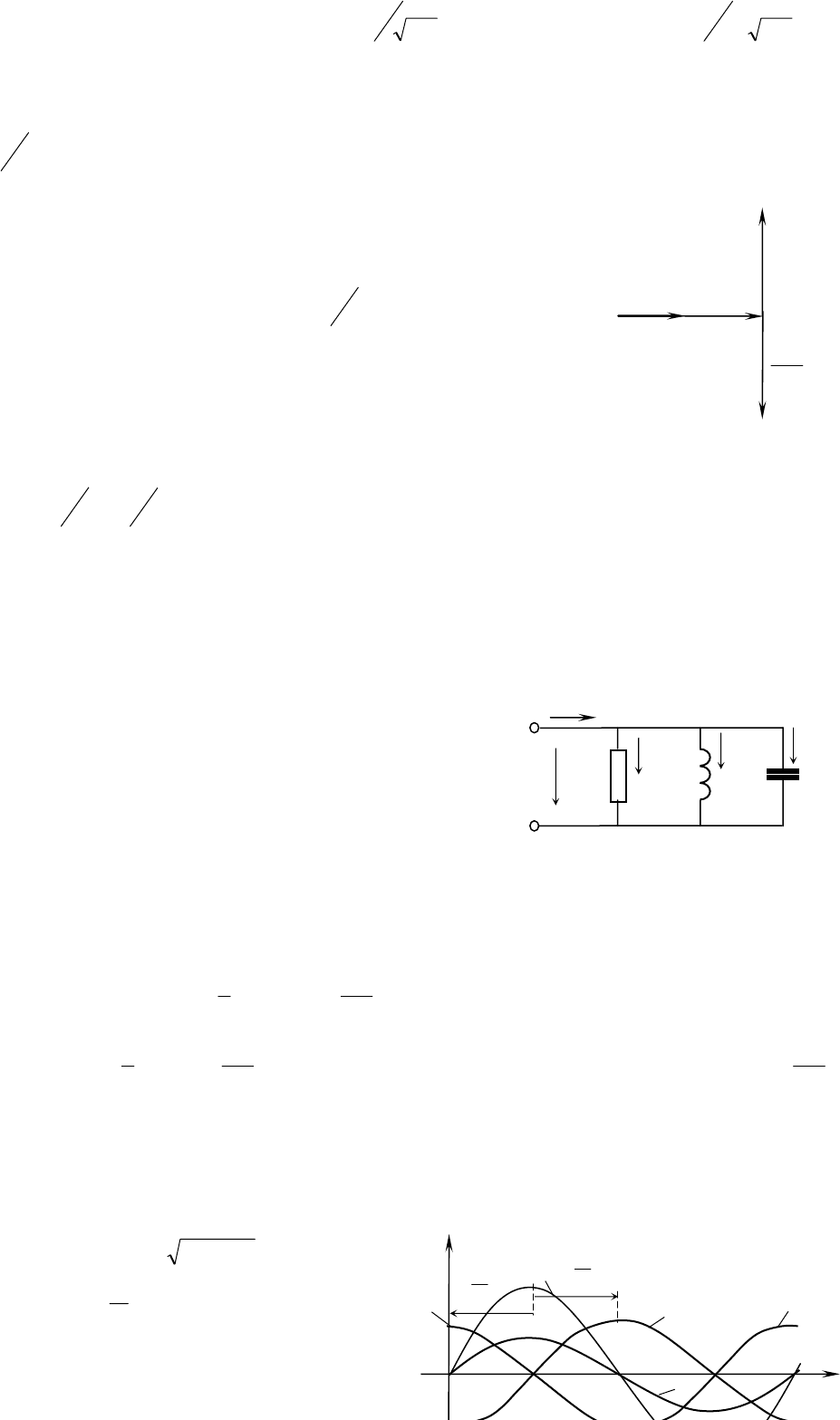
Векторная диаграмма напряжений при
резонансе представляется в виде прямой линии 0b
(рис.3.11в), так как векторы
IωL и
C
I
ω
равны между
собой, как это следует из условия резонанса. Полное
сопротивление цепи в этом случае имеет наименьшую
величину и равно активному ее сопротивлению. Угол
сдвига фаз
φ
между напряжением и током равен нулю.
Рис.3.11в
Для характеристики индуктивных катушек, представляемых цепью с
последовательным соединением элементов
r,L
, пользуются понятием добротности катушки
,
r
L
r
x
Q
L
L
ω
== которое равнозначно тангенсу угла сдвига фаз
φ
для катушки. Чем
меньше сопротивление
r
, тем выше при прочих равных условиях добротность контура.
Добротность индуктивных катушек, применяемых в электрических цепях, обычно не
превышает .300200
÷
=
L
Q
Для достижения более высокой добротности применяются чаще
всего пьезоэлектрические резонаторы.
3.8 ЦЕПИ С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
Если к зажимам электрической цепи, состоящей из
параллельно соединенных элементов
r,L,C
(рис.3.12), приложено синусоидальное напряжение
,sin
tUu
m
ω
= то синусоидальный ток, проходящий
через эту цепь, равен алгебраической сумме
синусоидальных токов в параллельных ветвях
(первый закон Кирхгофа): .
CLr
iiii
+
+=
Рис.1.12
Ток
r
i
в сопротивлении
r
совпадает по фазе с напряжением u, ток
L
i
в индуктивности
L
отстает, а ток
C
i
в емкости
C
опережает напряжение на
π/2
(рис.3.13).
Следовательно, суммарный ток i в цепи равен:
()
.
1
где ,cossincos
1
sin
1
coscos
1
sin
1
)sin(
C
L
bbbtbtgUtC
L
t
r
U
tCUtU
L
tU
r
tI
CLmm
mmmm
ω
ω
ωωωω
ω
ω
ωωω
ω
ωϕω
−=−=−=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−=
=+−=−
Величина
b
называется реактивной проводимостью цепи, которая в зависимости от
знака может иметь индуктивный
(b>0)
или емкостной
(b<0)
характер. В отличие от
реактивной проводимости
b
величина
g=1/r
, которая в данном случае называется активной
проводимостью, всегда положительна.
Для нахождения
m
I
и
φ
воспользуемся тригонометрическим соотношением
.
);sin(cossin
22
m
n
arctg
nmnm
=
±+=±
ϕ
ϕααα
i
r
i
C
u
L
r
L
i
C
i
Ir
b
0
0=
ϕ
I
LI
ω
C
I
ω
C
i
2
π
−
C
i
CLr
iii ,,
0
t
ω
r
i
L
i
u
2
π
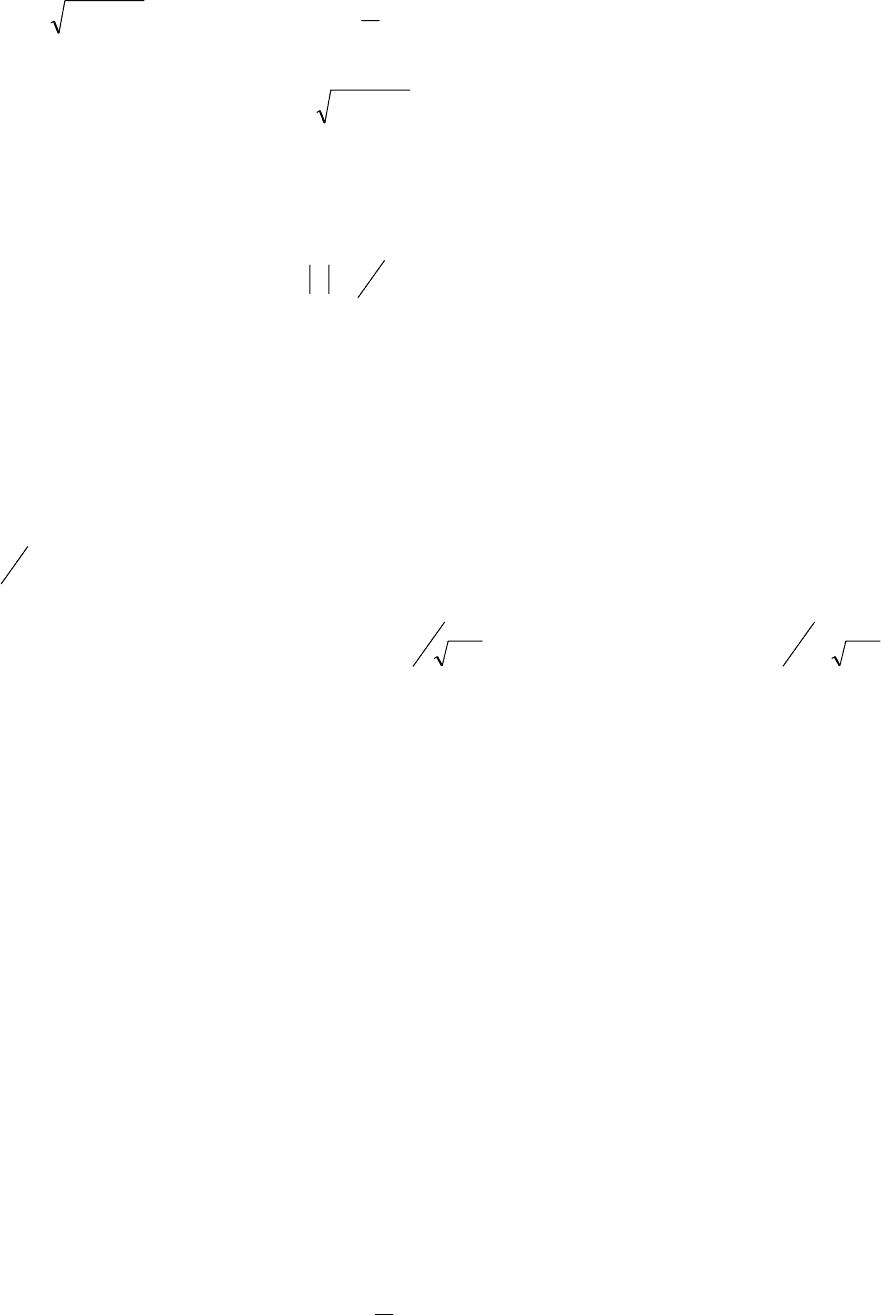
42
Тогда
.;
22
g
b
tgyUUbgI
mmm
==+=
ϕ
Откуда следует, что
−+===
22
где , или bgyyUIyUI
mm
полная проводимость рассматриваемой цепи.
Рис.3.13
Если задано напряжение )sin(
ψ
ω
+
=
tUu
m
на зажимах цепи с параллельным
соединением
r,L,C
, то ток определяется по формуле ).sin(
ϕ
ψ
ω
−+
=
tyUi
m
Угол φ, как и в
предыдущем случае, отсчитывается по оси углов
ωt
в направлении от напряжения к току и
является острым или прямым
.
2
π
ϕ
≤
Угол φ положителен при индуктивном характере цепи, то есть при
b>0
; при этом ток
отстает по фазе от напряжения. Угол
φ
отрицателен при емкостном характере цепи, то есть
при
b<0
; при этом ток опережает по фазе напряжение.
Ток совпадает с напряжением по фазе при ,0
=
−
=
CL
bbb
то есть при равенстве
индуктивной и емкостной проводимостей. Такой режим работы электрической цепи
называется резонансом токов.
Для нахождения угловой частоты, при которой может быть достигнуто совпадение по
фазе вектора тока с вектором напряжения, необходимо приравнять
C
b и
L
b
, то есть
.
1
C
L
ω
ω
=
Решая это уравнение относительно угловой частоты
ω,
величину которой для этого
случая обозначим
0
ω
, находим:
LC
1
0
=
ω
. Так как, ,2
00
f
π
ω
=
то .
2
1
0
LC
f
π
=
Получилась уже известная формула, определяющая собой частоту, при которой
наступает резонанс напряжений.
При малой величине активного сопротивления индуктивности и конденсатора, токи в
параллельных ветвях могут быть очень значительные, в то время как ток в неразветвленной
части цепи очень мал (определяется сопротивлением
r
для схемы на рис.3.12).
Для характеристики конденсаторов, представляемых цепью с параллельным
соединением элементов
r
и
C
, применяется понятие добротности конденсатора
,/
CrgbQ
CC
ω
== которое равнозначно тангенсу угла
|φ|
конденсатора. Чем больше
сопротивление
r
, тем больше (при прочих равных условиях) добротность конденсатора и тем
меньше потери. Добротность конденсаторов, применяемых в электрических цепях, обычно
определяется сотнями и тысячами.
3.9 МОЩНОСТЬ В ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Рассмотрим общий случай участка электрической цепи, напряжение на котором равно
).sin( ттоа ,sin
ϕ
ω
ω
−
=
=
tIitUu
mm
Мгновенная мощность, поступающая в цепь, состоит из двух слагающих:
[
]
,)2cos(cos)sin(sin
ϕ
ω
ϕ
ϕ
ω
ω
−
−
=−=
tUIttIUp
mm
постоянной величины
UIcosφ
и синусоидальной, имеющей удвоенную частоту по
сравнению с частотой напряжения и тока.
Среднее значение второй слагающей за время
T
, в течение которого она совершает
два цикла изменений, равно нулю. Поэтому активная мощность, поступающая в
рассматриваемый участок цепи,
.cos
1
0
ϕ
UIuidt
T
P
T
==
∫
Множитель
cosφ
носит название коэффициента мощности. Как видно из последней
формулы, активная мощность равна произведению действующих значений напряжения и
тока, умноженному на коэффициент мощности. Чем ближе угол
φ
к нулю, тем ближе
cosφ
к

43
единице и, следовательно, тем больше при заданных значениях
U
и
I
активная мощность
передается источником приемнику.
Произведение действующих значений тока и напряжения на зажимах цепи:
S=UI
,
называется полной мощностью цепи и измеряется в вольт-амперах (
ва
). Коэффициент
мощности равен отношению активной мощности к полной:
.cos
S
P
=
ϕ
При расчетах электрических цепей и на практике в эксплуатации пользуются
понятием реактивная мощность, которая вычисляется по формуле
Q=UIsinφ
и является
мерой потребления (или выработки) реактивного тока. Эта мощность измеряется в
реактивных вольт-амперах (
вар
).
3.10 КОМПЛЕКСНЫЙ МЕТОД РАСЧЕТА ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
Тригонометрическая форма расчета электрических цепей синусоидального тока
практически применяется только для простейших случаев. Более удобным расчетным
методом служит метод комплексных амплитуд (комплексный метод), основанный на замене
рассмотрения синусоидальных функций рассмотрением вращающихся векторов на
комплексной плоскости.
Ранее было показано, что законы Кирхгофа справедливы, если суммирование
действующих токов или напряжений вести в векторной
форме. Однако геометрическое
сложение векторов неудобно. В комплексном методе положение векторов на комплексной
плоскости определяется посредством комплексных чисел. Геометрическое суммирование
векторов заменяется алгебраическими операциями над комплексными числами, что
значительно проще и быстрее. После выполнения всех расчетов в комплексной форме, в
случае необходимости, можно вернуться к исходным синусоидальным функциям времени
путем
обратного перехода.
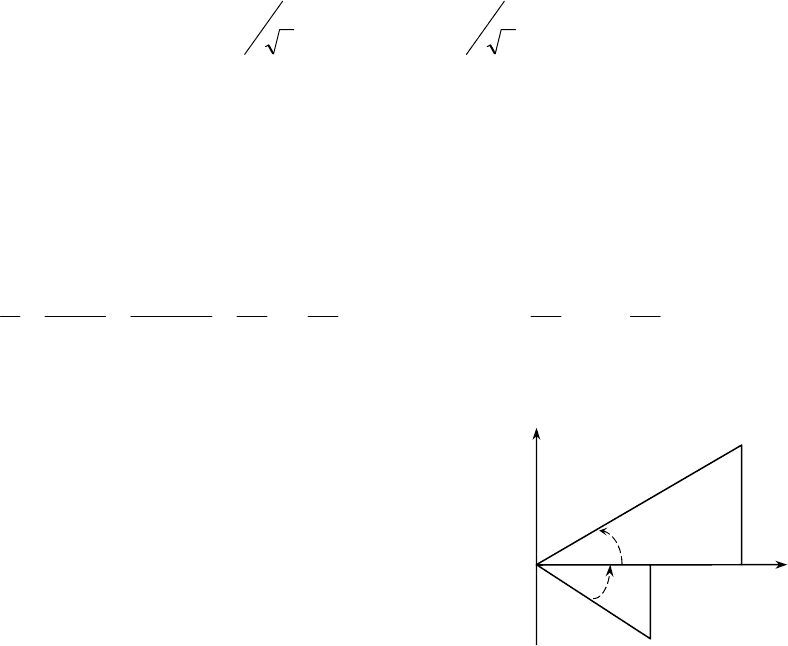
Построим вращающийся вектор на комплексной
плоскости и представим его показательной формой
комплексного числа. В этом случае модуль комплексного
числа должен быть постоянным, а аргумент – линейной
функцией времени. Вращающийся вектор, например, ток
(рис.3.14) в показательной форме комплексного числа
имеет вид:
1-j где ,
)(
==
+
i
tj
m
eIi
ψω
(
в электротехнике не пользуются обозначением i, так
как буква i обозначает ток
).
Рис.3.14
Комплексная величина
i
, зависящая от времени, модуль и аргумент которой равны,
соответственно, амплитуде и аргументу данного синусоидального тока, называется
комплексным мгновенным синусоидальным током. Аналогично можно представить
вращающийся вектор напряжения (рис.3.14)
.
)(
u
tj
m
eUu
ψω
+
=
Комплексная
величина
u
называется комплексным мгновенным синусоидальным напряжением.
Запись тока и напряжения в комплексном виде следует рассматривать как условное
(то есть символическое) изображение тока )sin(
im
tIi
ψ
ω
+
=
и напряжения
)sin(
um
tUu
ψ
ω
+= . Черточка над мгновенными значениями тока и напряжения отличает
комплексную форму мгновенных значений вращающихся векторов от обычной формы
мгновенных значений токов и напряжений.
Комплексные ток и напряжение можно представить иначе:
.; где ,;
uiui
j
mm
j
mm
tj
m
tj
j
m
tj
m
tj
j
m
eUUeIIeUeeUueIeeIi
ψψ
ωω
ψ
ωω
ψ
======
&&&&
Величины
mm
UI
&&
,
называются комплексными амплитудами.
Разделив комплексные амплитуды тока и напряжения на
2, получим,
соответственно, комплексный ток
I
&
и комплексное напряжение U
&
:
0
u
j
UeU
ψ
=
&
i
j
IeI
ψ
=
&
u
ψ
i
ψ
j
+
44
.
2
;
2
ui
j
m
j
m
Ue
U
UIe
I
I
ψψ
====
&
&
&
&
Точка над действующим или амплитудным значением напряжения или тока отличает
комплексную форму записи этих величин от обычной.
Закон Ома в комплексной форме можно записать в следующем виде:
ZIU
&&
=
.
Комплексная величина
Z
, равная отношению комплексного напряжения на зажимах
электрической цепи к комплексному току в этой цепи, называется комплексным
сопротивлением. Комплексное сопротивление можно представить в тригонометрической и
алгебраической формах:
Z=zcosφ+jzsinφ=r+jx
. Величина обратная
Z,
называется
комплексной проводимостью и равна:
., где,
11
222222
z
x
b
z
r
gjbg
z
x
j
z
r
xr
jxr
jxrZ
Y ==−=−=
+
−
=
+
==
g — активная проводимость цепи, b — реактивная проводимость цепи.
На рис.3.15 показан пример расположения на
комплексной плоскости комплексных сопротивления и
проводимости для цепи индуктивного характера. Для
индуктивной цепи комплексная проводимость имеет
отрицательную мнимую часть.
Законы Кирхгофа также могут быть
представлены в комплексной форме.
Первый и второй
законы Кирхгофа для переменного тока должны быть
написаны в виде:
∑∑∑
===
==
m
k
p
k
kk
n
k
k
UEI
111
.;0
&&&
Рис.3.15
3.11 ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ РЕАКТИВНЫХ
ДВУХПОЛЮСНИКОВ
Как отмечалось в разделе 2.4, двухполюсником называется любая электрическая цепь или
часть электрической цепи, имеющая два вывода. Различают двухполюсники активные и
пассивные. Здесь рассматриваются только пассивные двухполюсники. По числу элементов,
входящих в двухполюсник, различают одноэлементный, двухэлементный и
многоэлементный двухполюсники. По характеру этих элементов двухполюсники делятся на
реактивные, то есть состоящие из индуктивностей
и емкостей, и двухполюсники с потерями,
содержащие активные сопротивления. Реактивные двухполюсники представляют собой
идеализированные электрические схемы, приближающиеся пор своим свойствам к
физически существующим цепям с малыми потерями.
Частотные характеристики сопротивлений или проводимостей двухполюсников,
образующих электрическую цепь, предопределяют частотные и резонансные свойства цепи,
то есть зависимости амплитуд и фаз токов и
напряжений от частоты.
3.11.1 Одноэлементные реактивные двухполюсники
Индуктивность и емкость представляют собой простейшие одноэлементные
реактивные двухполюсники. Знак комплексного сопротивления и комплексной
проводимости каждого из этих двухполюсников не зависит от частоты; этим они
существенно отличаются от других, более сложных реактивных двухполюсников,
содержащих неоднородные реактивные элементы, то есть индуктивность и емкость в разных
сочетаниях.
z
j
x
ϕ
ϕ
y
b
r
1
+
0
g
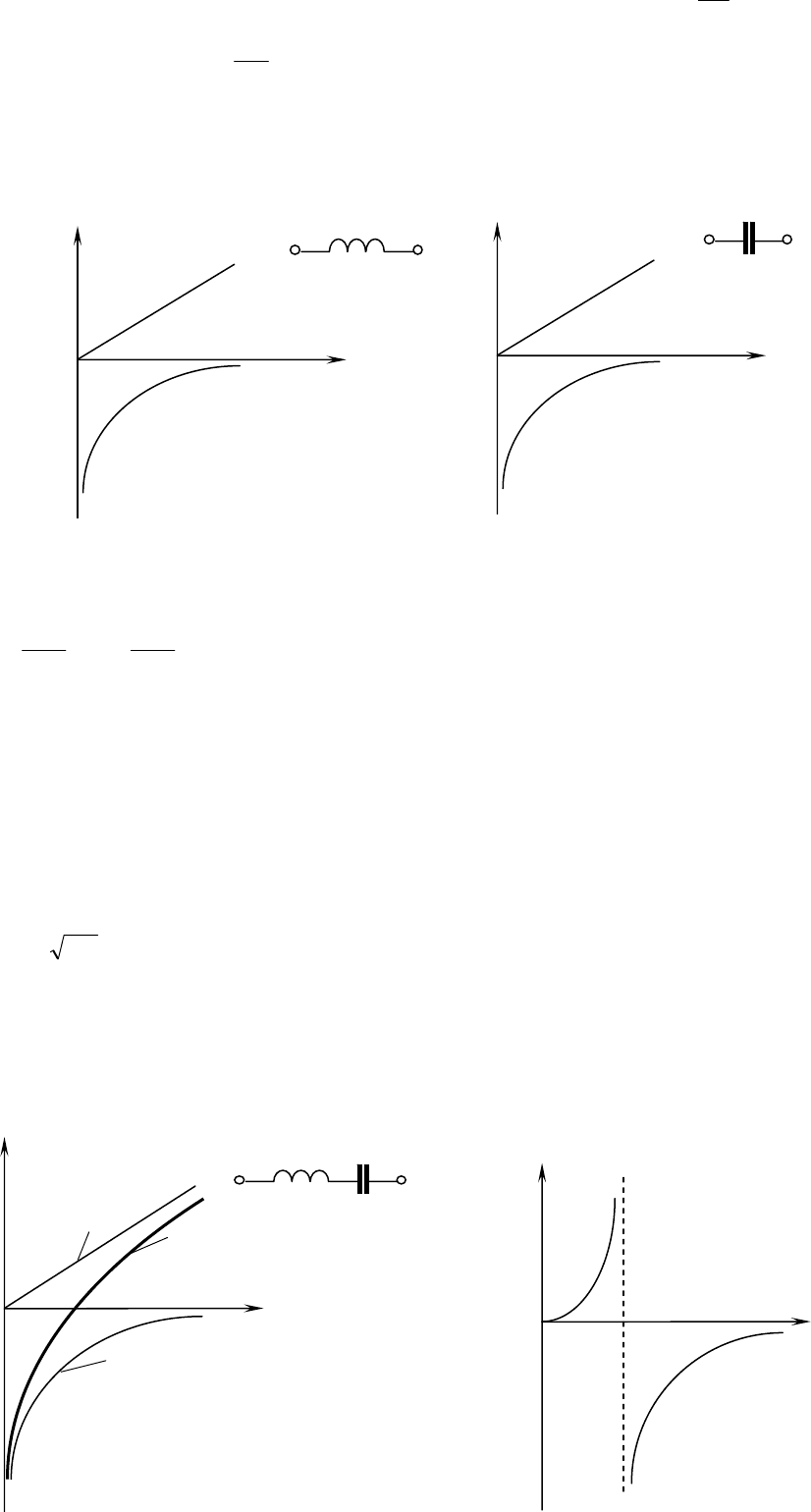
45
Во всем спектре частот комплексные сопротивление и проводимость для
индуктивного элемента имеют вид
;
1
;
L
jjbYLjjxZ
LLLL
ω
ω
−=−===
для емкостного
элемента
.;
1
CjjbY
C
jjxZ
CCCC
ω
ω
==−=−=
Частотные характеристики
CL
YZ
и
, построенные в прямоугольной системе
координат, представляют собой прямые линии, а частотные характеристики
LC
YZ
и -
равнобочные гиперболы (рис.3.16).
Рис.3.16
Следует заметить, что как сопротивления, так и проводимости одноэлементных
реактивных двухполюсников возрастают (с учетом знака) по мере повышения частоты, то
есть
.0;0 >>
ωω
jd
dY
jd
dZ
Это является общим свойством всех реактивных двухполюсников, а не только
одноэлементных.
3.11.2 Двухэлементные реактивные двухполюсники
Двухэлементные двухполюсники, составленные из индуктивности и емкости,
представляют собой простейшие резонансные цепи.
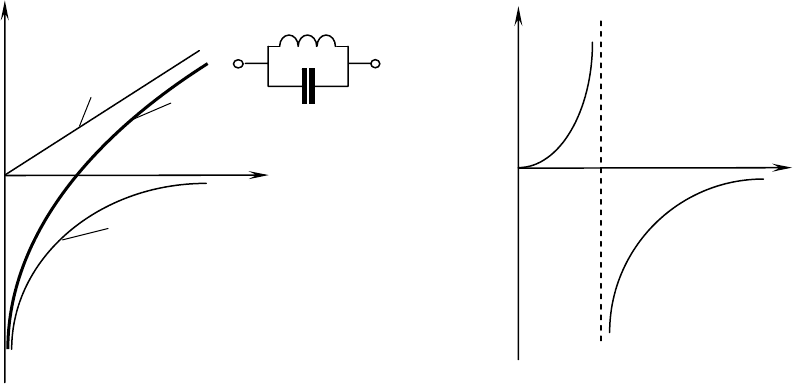
При последовательном соединении индуктивности и емкости алгебраически
складываются комплексные сопротивления. На рис.3.17а жирной линией показана частотная
характеристика двухполюсника, она пересекает ось абсцисс при резонансной частоте
LC/1
0
=
ω
(резонанс напряжений). Эта частота, при которой функция
CL
ZZZ
+
=
обращается в нуль, называется нулем данной функции. Частотная характеристика
проводимости того же двухполюсника представляет собой функцию, обратную
сопротивлению:
ZY /1
=
. Кривая Y показана на рис.3.17б. При резонансной частоте
проводимость рассматриваемого двухполюсника обращается в бесконечность; эта точка
носит название полюса функции Y.
В области частот ниже резонансной
(
)
0
ω
ω
<
сопротивление емкостного элемента
превышает по абсолютной величине сопротивление индуктивного элемента; при этом
сопротивление двухполюсника имеет емкостной характер.
Рис 3.17а Рис.3.17б
L
L
Z
j+
ω
j−
0
L
Y
C
Z
j
+
ω
j
−
0
C
Y
C
C
L
C
Z
j+
ω
j−
0
L
Z
CL
ZZ +
0
ω
Z
0
j
+
ω
j
−
Y
0
ω
46
L
Y
j+
ω
j−
0
C
Y
Y
0
ω
Y
В области частот выше резонансной
(
)
0
ω
ω
>
абсолютная величина емкостного
сопротивления меньше величины индуктивного; сопротивление двухполюсника имеет
индуктивный характер.
При параллельном соединении индуктивности и емкости алгебраически
складываются их комплексные проводимости. На рис.3.18а жирной линией показана
частотная характеристика двухполюсника. Частотная характеристика сопротивления того же
двухполюсника представляет собой функцию, обратную проводимости:
YZ /1=
. Кривая Z
показана на рис.3.18б. Частота, при которой характеристика Y пересекает ось абсцисс (нуль
функции Y), а характеристика Z уходит в бесконечность (полюс функции Z), является
резонансной частотой (резонанс токов).
Рис.3.18а Рис.3.18б
В области частот ниже резонансной проводимость индуктивного элемента
перекомпенсирует проводимость емкостного элемента и сопротивление двухполюсника
получается индуктивным. В области частот выше резонансной наблюдается обратное
явление и сопротивление двухполюсника имеет емкостной характер.
3.11.3 Многоэлементный реактивный двухполюсник
Многоэлементный реактивный двухполюсник может быть получен в результате
различных сочетаний одноэлементных и двухэлементных двухполюсников.
Из свойства положительности производной dZ/jdω (или dY/jdω) следует, что нули и
полюса функции Z (или Y) должны чередоваться, так как при наличии двух
последовательных нулей, не разделенных полюсом, имелся бы участок характеристики с
отрицательной производной.
В общем случае
, если при ω=0 сопротивление реактивного двухполюсника равно
нулю, то есть имеется путь для постоянного тока, то первым наступает резонанс токов, за
ним следует резонанс напряжений и так далее. В противном случае порядок расположения
резонансов обратный: первым наступает резонанс напряжений, вторым – резонанс токов и
так далее. У реактивных двухполюсников сумма полюсов
и нулей (не считая точек ω=0 и
ω=
∞
) на единицу (или более) меньше числа элементов двухполюсника.
3.12 ЧЕТЫРЁХПОЛЮСНИКИ
При анализе электрических цепей в задачах исследования взаимосвязи между
переменными (токами, напряжениями, мощностями и т.п.) двух каких-то ветвей схемы
широко используется теория четырехполюсников.
Четырехполюсник
– это часть схемы
произвольной конфигурации, имеющая две пары зажимов (отсюда и произошло его
название), обычно называемые входными и выходными.
0
j
+
ω
j
−
Z
0
ω
C
L
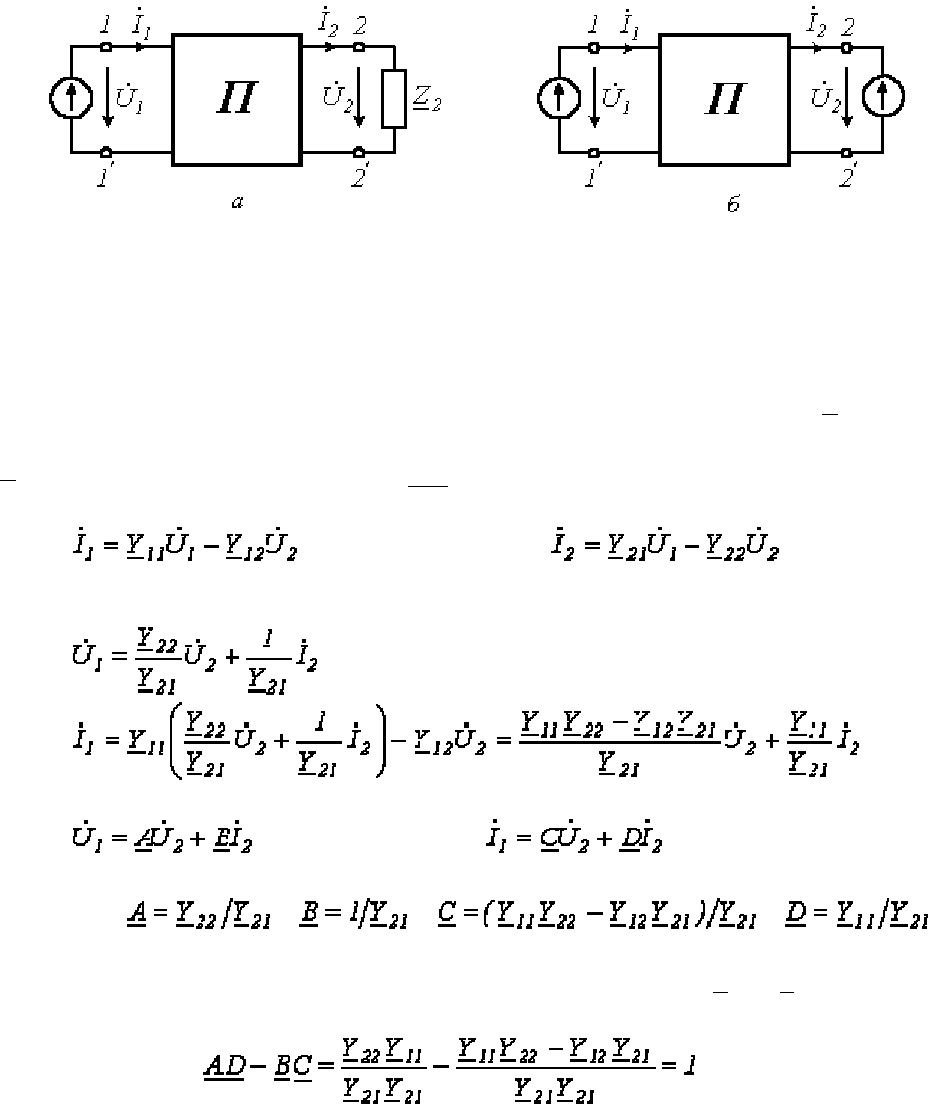
47
Примерами четырехполюсника являются трансформатор, усилитель, потенциометр,
линия электропередачи и другие электротехнические устройства, у которых можно выделить
две пары полюсов.
Рис. 3.19
В общем случае четырехполюсники можно разделить на
активные,
в структуру
которых входят источники энергии, и
пассивные,
ветви которых не содержат источников
энергии.
Ниже будут рассмотрены элементы теории пассивных четырехполюсников. Для
записи уравнений четырехполюсника выделим в произвольной схеме ветвь с единственным
источником энергии и любую другую ветвь с некоторым сопротивлением
2
Z (см. рис.
3.19а). В соответствии с принципом компенсации заменим исходное сопротивление
2
Z источником с напряжением
2
22
ZIU
&&
= (см. рис. 3.19б). Тогда на основании метода
наложения для цепи на рис. 3.19б можно записать
;
Решая полученные уравнения относительно напряжения и тока на первичных
зажимах, получим
или
(3.2)
где
; ; ; —
коэффициенты четырехполюсника
.
Учитывая, что в соответствии с принципом взаимности
2112
YY = , видно, что
коэффициенты четырехполюсника связаны между собой соотношением
(3.3)
Уравнения (3.1) и (3.2) представляют собой основные уравнения четырехполюсника;
их также называют уравнениями четырехполюсника в А-форме (см. табл. 3.1). Существует
шесть форм записи уравнений пассивного четырехполюсника. Действительно,
четырехполюсник характеризуется двумя напряжениями
1
U
&
,
2
U
&
и двумя токами
1
I
&
и
2
I
&
.
Любые две величины можно выразить через остальные. Так как число сочетаний из четырех
по два равно шести, то и возможно шесть форм записи уравнений пассивного
четырехполюсника, которые приведены в табл. 3.1. Положительные направления токов для
различных форм записи уравнений приведены на рис. 3.20.
(3.1)

48
Рис. 3.20
Выбор той или иной формы уравнений
определяется областью и типом решаемой задачи.
Если при перемене местами источника и
приемника энергии их токи не меняются, то такой
четырехполюсник называется
симметричным.
Как видно из сравнения А- и В- форм в табл. 3.1,
это выполняется при
DA
=
. Четырехполюсники,
не удовлетворяющие данному условию,
называются
несимметричными.
При практическом использовании уравнений четырехполюсника для анализа цепей
необходимо знать значения его коэффициентов. Коэффициенты четырехполюсника могут
быть определены экспериментальным или расчетным путями. При этом в соответствии с
соотношением (3.3) определение любых трех коэффициентов дает возможность определить и
четвертый.
Один из наиболее удобных экспериментальных методов определения коэффициентов
четырехполюсника основан на опытах
холостого хода и короткого замыкания при питании
со стороны вторичных зажимов и опыте холостого хода при питании со стороны первичных
зажимов. В этом случае при 0I
2
=
&
на основании уравнений (3.1) и (3.2)
.
При 0I
1
=
′
&
Таблица 3.1.
Формы записи уравнений пассивного
четырехполюсника
Форма
Уравнения
Связь с коэффициентами
основных уравнений
А-форма
;
;
Y-форма
;
;
; ;
; ;
Z-форма
;
;
; ;
; ;
Н-форма
;
;
; ;
; ;
G-форма
;
;
; ;
; ;
B-форма
;
.
; ;
; .
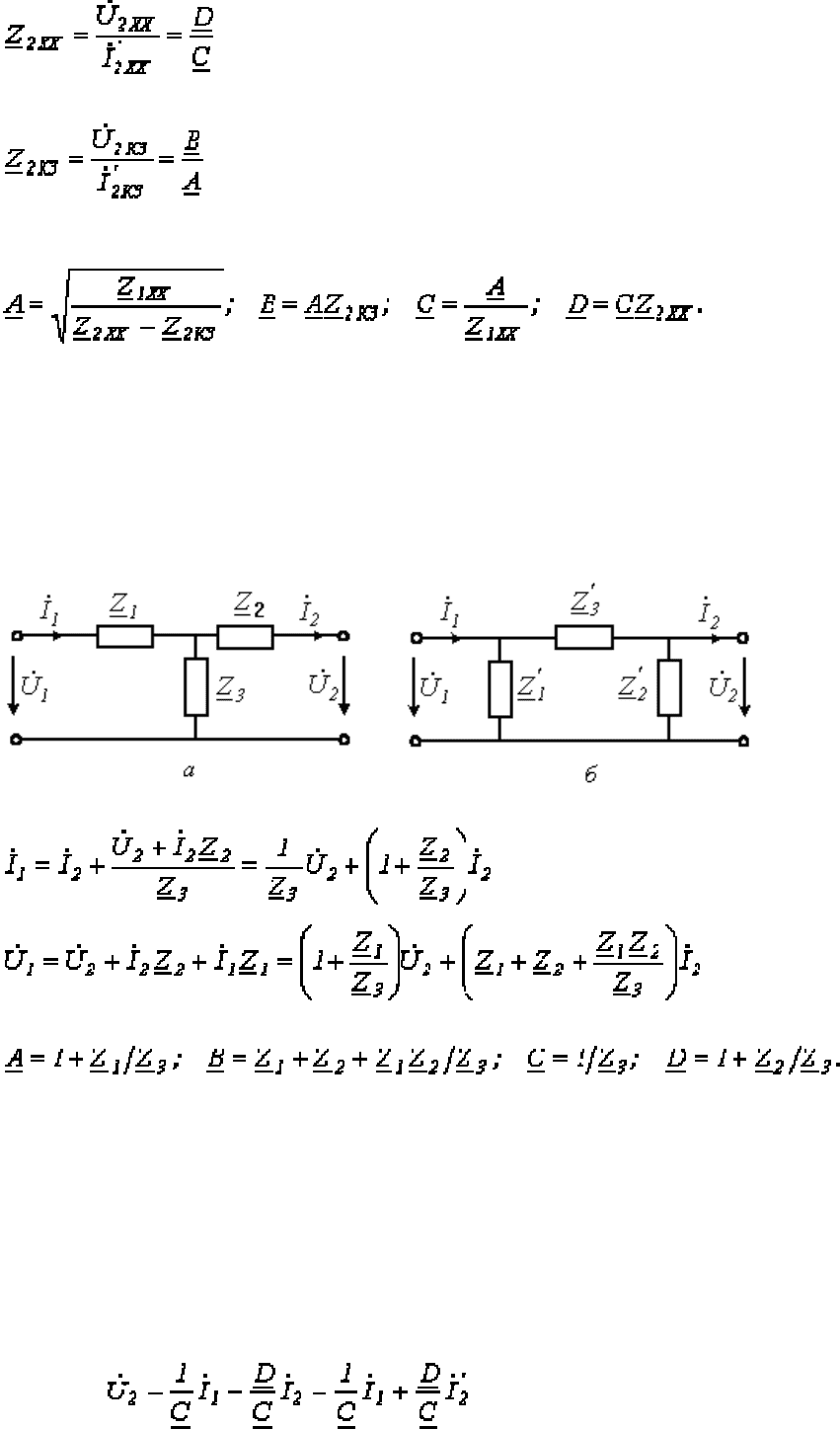
49
Решение этих уравнений относительно коэффициентов четырехполюсника дает:
При определении коэффициентов четырехполюсника расчетным путем должны быть
известны схема соединения и величины сопротивлений четырехполюсника. Так как
пассивный четырехполюсник характеризуется тремя независимыми постоянными
коэффициентами, следовательно, пассивный четырехполюсник можно представить в виде
трехэлементной эквивалентной
Т
- (рис. 3.21а) или
П-образной
(рис. 3.21б)
схемы
замещения.
Для определения коэффициентов четырехполюсника для схемы на рис. 3.21а с
использованием первого и второго законов Кирхгофа выразим
1
U
&
и
1
I
&
через
2
U
&
и
2
I
&
:
Рис. 3.21
;
.
Сопоставление полученных выражений с соотношениями (3.1) и (3.2) дает:
Коэффициенты четырехполюсника для схемы на рис. 3.21б могут быть определены
аналогично или на основании полученных для цепи на рис. 3.21а с использованием
рассмотренных ранее формул преобразования “ звезда-треугольник”.Из вышесказанного
можно сделать вывод, что зная коэффициенты четырехполюсника, всегда можно найти
параметры Т- и П-образных схем его замещения. На практике
часто возникает потребность в
переходе от одной формы записи уравнений четырехполюсника к другой. Для решения этой
задачи, т.е. чтобы определить коэффициенты одной формы записи уравнений через
коэффициенты другой, следует выразить какие-либо две одинаковые величины в этих
формулах через две остальные и сопоставить их с учетом положительных направлений токов
для
каждой из этих форм. Так при переходе от А- к Z-форме на основании (3.2) имеем
При 0U
1
=
&
.
.
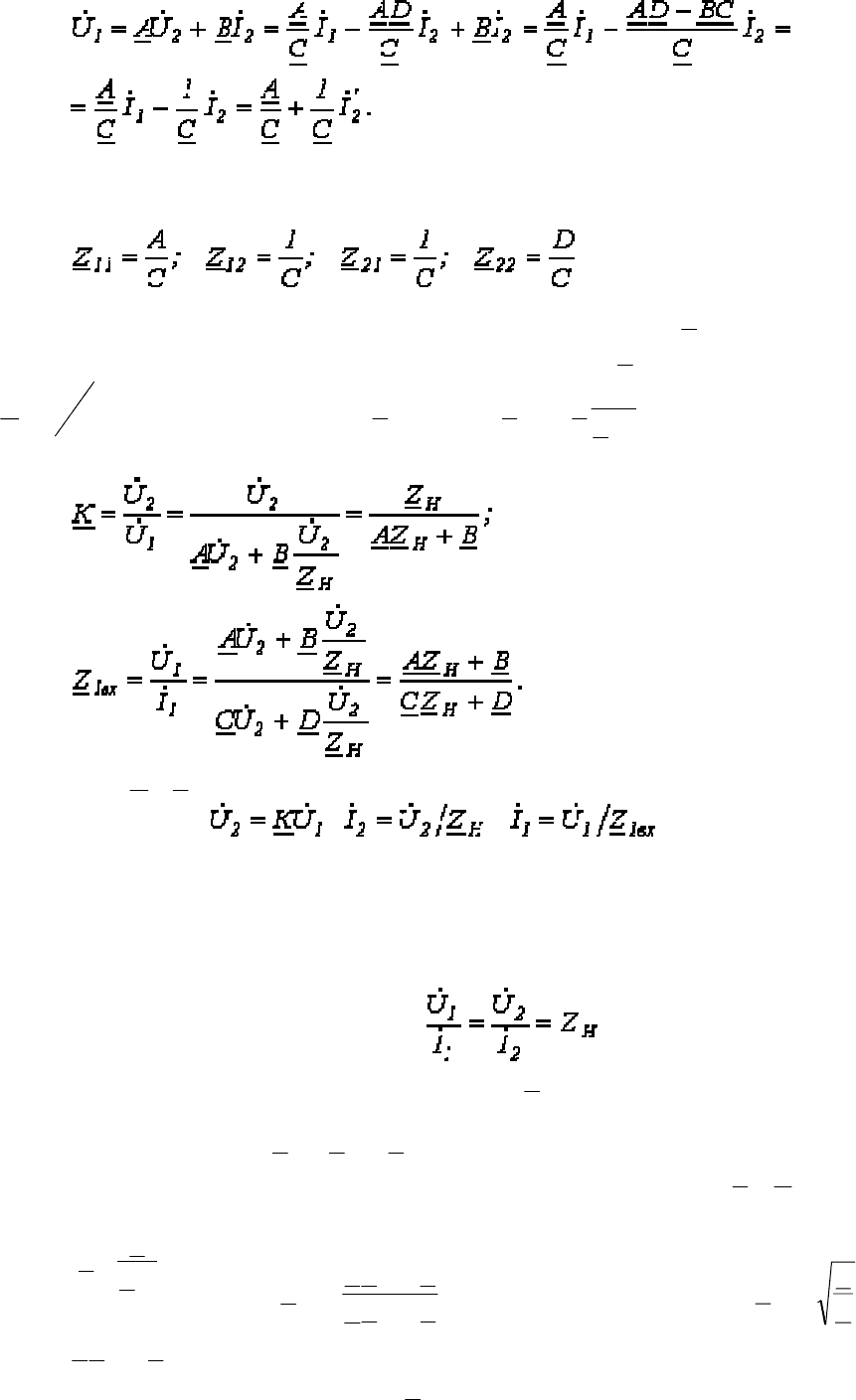
50
Подстановка этого соотношения в (3.1) дает
.
Сопоставляя полученные выражения
2
U
&
и
1
U
&
с уравнениями четырехполюсника в
Z-форме (см. табл. 3.1), получим
.
При анализе работы четырехполюсника на нагрузку
Н
Z удобно использовать
понятие входного сопротивления с первичной стороны
в
х
1
Z и коэффициента передачи
1
2
U
U
K
&
&
= . Учитывая, что
Н
ZIU
22
&&
= и
Н
Z
U
BUAU
2
21
&
&&
+=
, для этих параметров можно
записать:
Зная
K
,
в
х
1
Z и
1
U
&
, можно определить остальные переменные на входе и выходе
четырехполюсника:
; ; .
3.12.1 Характеристическое сопротивление и коэффициент
распространения симметричного четырехполюсника
В электросвязи широко используется режим работы симметричного
четырехполюсника, при котором его входное сопротивление равно нагрузочному, т.е.
Это сопротивление обозначают как
C
Z и называют
характеристическим
сопротивлением
симметричного четырехполюсника, а режим работы четырехполюсника,
для которого справедливо
НвхC
ZZZ
=
=
,
называется
режимом согласованной нагрузки.
В указанном режиме для симметричного четырехполюсника
)DA( = на основании
(3.1) и (3.2) можно записать
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
2
C
1
2
C
1
IAZCI
U
Z
B
AU
&&
&&
Разделив соотношение
1
U
&
на
1
I
&
, получаем уравнение,
AZC
BZA
Z
C
C
C
+
+
=
,
решением которого является
C
B
Z
C
=
.
Подставив полученное решение
C
Z
в начальную систему, система приобретают вид :
