Лукоянычев В.Г. Электротехника
Подождите немного. Документ загружается.


21
Рис.2.2
Проводимости ветвей соответственно равны:
.
1
;
1
;
1
3
3
2
2
1
1
R
G
R
G
R
G ===
Для заданной электрической цепи с тремя узлами могут быть записаны два уравнения по первому
закону Кирхгофа:
для узла 1
()
(
)
(
)
;0;GGGGGI
3231312133111
=
−
+
=
−
+
−
=
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
для узла 2
()
(
)
(
)
;0;
3132321233222
=
−
+
=
−
+
−=
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
GGGGGI
величина
31
GG +
, представляющая собой сумму проводимостей ветвей, сходящихся в узле 1, называется
проводимостью узла 1; величина
3
G
, равная проводимости ветви между узлами 1 и 2, входящая в уравнения со
знаком минус, называется общей проводимостью между узлами 1 и 2.
Если заданы токи источников тока и проводимости ветвей, то узловые потенциалы находятся
совместным решением уравнений. В общем случае если электрическая схема содержит
q
узлов, то на
основании первого закона Кирхгофа получается система из
q-1
уравнений (узел
q
принят за базисный):
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=+++
=+++
=+++
−−−−−−−
−−
−−
;
;
;
1,11,112,121,11
221,21222211
111,11122111
qqqqqqq
qq
qq
IGGG
IGGG
IGGG
ϕϕϕ
ϕϕϕ
ϕϕϕ
K
KKKK
K
K
kk
I
— узловой ток k-го узла. Здесь ток источника тока, проходящий к узлу, включается в ток
kk
I
со
знаком плюс, а отходящий от узла – со знаком минус;
kk
G
— собственная проводимость всех ветвей, сходящихся в данном узле
k
;
ki
G
— общая проводимость между узлами
k
и
i
, входящая со знаком минус.
Решив систему уравнений при помощи определителей, получим формулу для потенциала k-го узла
относительно базиса:
*)*(*,
1
1
1
∑
−
=
∆
∆
=
q
i
ikiik
I
ϕ

22
где
∆
—
определитель системы,
ik
∆
— алгебраическое дополнение элемента
ik
G
главного
определителя системы.
Система уравнений, выражающая первый закон Кирхгофа, записана в предположении, что в качестве
источников электрической энергии служат источники тока. При наличии в электрической схеме источников
напряжения последние должны быть заменены эквивалентными источниками тока.
Если в схеме имеются ветви, содержащие только э.д.с. (проводимости таких ветвей бесконечно
велики),
то эти ветви следует рассматривать как источники неизвестных токов, которые затем исключаются при
сложении соответствующих уравнений. Дополнительными связями между неизвестными узловыми
потенциалами будут являться известные напряжения между узлами, равные заданным э.д.с.
При наличии только одной ветви с э.д.с. и бесконечной проводимостью целесообразно принять за
базисный узел один
из узлов, к которому примыкает данная ветвь; тогда потенциал другого узла становится
известным и число неизвестных сокращается на одно.
Метод узловых потенциалов имеет преимущество перед методом контурных токов в том случае, когда
число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму
закону Кирхгофа. Если заданная электрическая
схема имеет
q
узлов и
p
ветвей, то в соответствии со сказанным
выше, метод узловых потенциалов представляет преимущество при
q-1<p-q+1
, или при
2(q-1)<p
.
Здесь имеется в виду общий случай, когда число уравнений не сокращается за счет известных
контурных токов или узловых потенциалов.
2.3 МЕТОД НАЛОЖЕНИЯ
В линейной электрической цепи, содержащей источники напряжения, контурные токи (и
соответственно токи в ветвях) представляют собой линейные функции контурных э.д.с.
Математически они выражаются формулой (**):
ik
n
1k
kkii
E
1
I
∆
∆
∑
=
=
Физический смысл этой формулы заключается в том, что ток в любом контуре линейной
электрической цепи может быть получен как алгебраическая сумма токов, вызываемых в
этом контуре каждой из э.д.с. в отдельности.
Метод расчета токов, основанный на определении токов в одном и том же контуре
(или ветви) при поочередном
воздействии э.д.с. и последующем алгебраическом сложении
токов, называется методом наложений.
При определении частичных слагающих токов по методу наложения необходимо
считать включенными внутренние сопротивления тех источников напряжения, которые
принимаются отсутствующими при вычислении слагающих токов. Если в цепи заданы

23
источники э.д.с., то есть внутренние сопротивления источников равны нулю, то при
определении токов, вызываемых какой-либо э.д.с., все остальные источники э.д.с.
закорачиваются.
В линейной электрической цепи, содержащей источники тока, узловые потенциалы
(и, соответственно, напряжения на ветках) представляют собой линейные функции
задающих токов источников. Математически
они выражаются формулой (***):
∑
−
=
∆
∆
=
1
1
.
1
q
i
ikiik
I
ϕ
Физический смысл этой формулы заключается в том, что узловой потенциал любого
узла линейной электрической цепи может быть получен как алгебраическая сумма
напряжений, вызываемых в этом узле каждым из задающих токов в отдельности. Таким
образом, формула (***), так же как и (**), представляет собой математическую запись
метода наложения, справедливого для линейных электрических цепей.
При
определении частичных слагающих узловых напряжений по методу наложения
необходимо считать включенными внутренние проводимости тех источников тока, которые
принимаются отсутствующими при вычислении слагающих напряжений. Если источники
тока заданы без внутренних проводимостей, то есть проводимости их равны нулю, то при
пользовании методом наложения ветви с неучтенными источниками тока разрываются.
Если в линейной
электрической цепи заданными являются одновременно источники
напряжения и источники тока, то метод наложения применим и в этом случае. Например, ток
в каком-либо контуре данной цепи может быть получен в результате алгебраического
сложения токов, вызываемых в этом контуре поочередным действием источников
напряжения и тока. При этом отсутствующие источники напряжения заменяются
внутренними
сопротивлениями, а отсутствующие источники тока – внутренними
проводимостями.
2.4 МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА
Этот метод целесообразно применять в тех случаях, когда необходимо определить ток в одной ветви
сложной линейной электрической цепи. Особенно метод удобен при определении тока в одной ветви, когда
сопротивление этой ветви изменяется.
В любой электрической схеме всегда можно выделить одну ветвь, а всю остальную часть обозначить
прямоугольником. По отношению к
выбранной ветви вся схема представляет собой двухполюсник.
Двухполюсник – это обобщенное название
схемы, которая своими двумя выходами (полюсами)
присоединяется к выделенной ветви.
Двухполюсники бывают активными (рис.2.3а), если
они содержат источники напряжения и/или тока, и
пассивными (рис.2.3б), если они состоят только из
пассивных элементов.
Рис.2.3а Рис.2.3
б
I
R
m
n
A
R
I
m
n
E
П
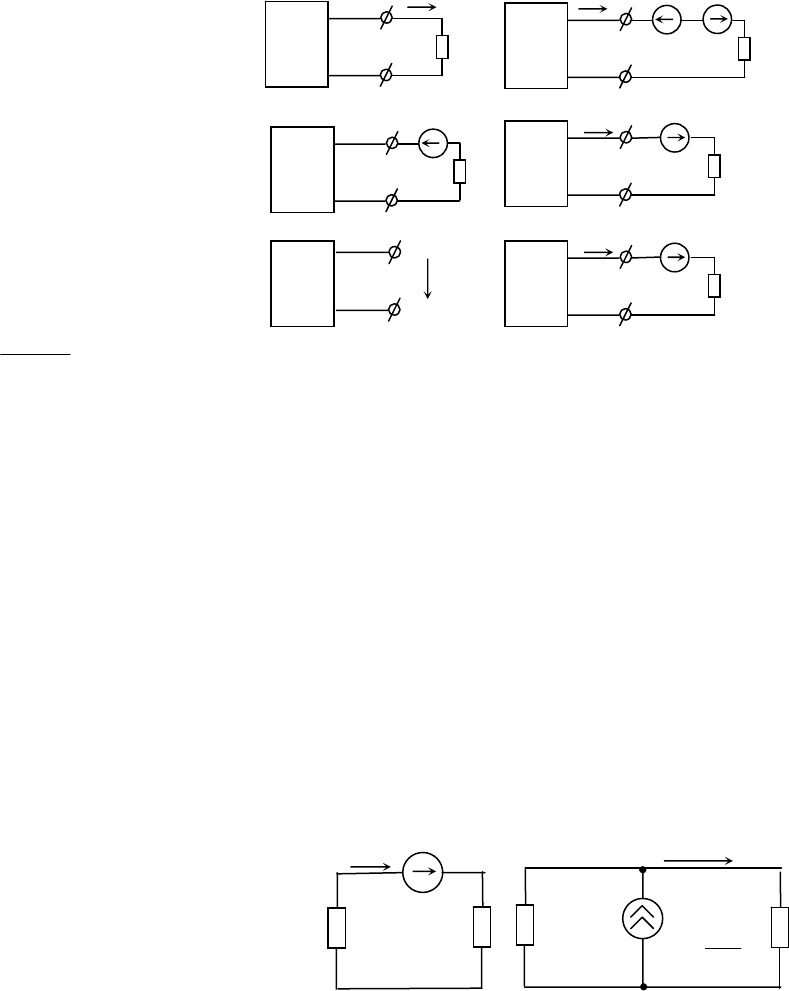
24
Сущность метода заключается в том, что ветвь сложной цепи, в которой необходимо определить ток,
следует рассматривать как нагрузку для некоторого эквивалентного генератора, которым является вся
остальная часть электрической цепи, состоящей из источников и пассивных элементов (двухполюсник).
Этот метод опирается на теорему об эквивалентном источнике, у которой существует два варианта:
вариант
с источником напряжения и вариант с источником тока.
2.4.1 Теорема об эквивалентном источнике напряжения
Ток в любой ветви mn линейной электрической цепи не изменится, если
электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным
источником напряжения; э.д.с. этого источника должна быть равна напряжению на зажимах
разомкнутой ветви mn, а внутреннее сопротивление источника должно равняться входному
сопротивлению пассивной электрической цепи со стороны зажимов m и
n при разомкнутой
ветви mn.
Данная теорема доказыва-
ется следующим образом: в ветвь
mn вводятся две равные по вели-
чине и противоположно направлен-
ные э.д.с.
mn
U при условии, что
mn
U равно напряжению между за-
жимами m и n при разомкнутой
ветви mn. То есть напряжению хо-
лостого хода (рис.2.4).
Применение метода наложе-
ния в соответствии с рис.2.4 приво-
дит к выводу, что ток в ветви R
равен:
.
0
RR
U
I
mn
+
=
Рис.2.4
0
R — сопротивление всей пассивной цепи П. Таким образом, ток в ветви R получается в
предположении, что данная ветвь подключена к источнику напряжения, э.д.с. которого равна
mn
U , а внутреннее сопротивление равно
0
R .
При наличии в электрической цепи нескольких источников э.д.с. и тока напряжение
холостого хода является линейной функцией заданных э.д.с. и токов источников.
2.4.2 Теорема об эквивалентном источнике тока
Ток в любой ветви mn линейной электрической цепи не изменится, если
электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным
источником тока; ток этого источника должен быть равен току, проходящему между
зажимами m и n , замкнутыми накоротко, а внутренняя проводимость источника должна
равняться входной проводимости пассивной электрической цепи со стороны зажимов m и n
при
разомкнутой ветви mn.
Данное положение вытекает из условия
эквивалентности источников напряжения
и тока, а именно: источник напряжения,
э.д.с. которого равна напряжению холо-
n
m
mn
U
I
R
m
n
A
=
R
I
m
n
A
mn
U
mn
U
=
R
m
n
A
mn
U
+
=
=
+
R
I
m
n
mn
U
П
=
R
I
m
n
mn
U
П
A
mn
U
I
0
R
R
R
0
R
U
I
mn
mn
=
0
R
I

25
стого хода
mn
U
, а внутреннее сопротив-
ление равно
0
R
(рис.2.5а), может быть
заменен источником тока (рис.2.5б):
.
0
0
mn
mn
mn
UG
R
U
I
==
Рис.2.5а Рис.2.5б
Последнее выражение есть не что иное, как ток, проходящий между зажимами
m
и
n
,
замкнутыми накоротко (ток короткого замыкания). Искомый ток в цепи равен:
.
1
где,
00
0
R
GI
GG
G
I
RR
R
I
mnmn
=
+
=
+
=
При наличии в электрической цепи нескольких источников тока и э.д.с. ток короткого
замыкания является линейной функцией заданных э.д.с. и токов источников.
Метод эквивалентного генератора эффективен при экспериментальных
исследованиях. Для определения внутреннего сопротивления
0
R
можно использовать
короткое замыкание между зажимами
m
и
n
: .
0
mn
mn
I
U
R
= Таким образом, последовательность
определения тока в нагрузке (ток в ветви
R
) необходимо замерить напряжение холостого
хода
ХХ
U
на зажимами
m
и
n
, а затем ток короткого замыкания
КЗ
I
на тех же зажимах.
Искомый ток в нагрузке будет равен:
.
RI/U
U
RI/U
U
I
КЗXX
ХХ
mnmn
mn
+
=
+
=
Поэтому данный метод еще называют – метод холостого хода и короткого замыкания.
2.5 ПРИМЕРЫ РАСЧЕТА ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
2.5.1 Расчет электрической цепи на основе законов Кирхгофа
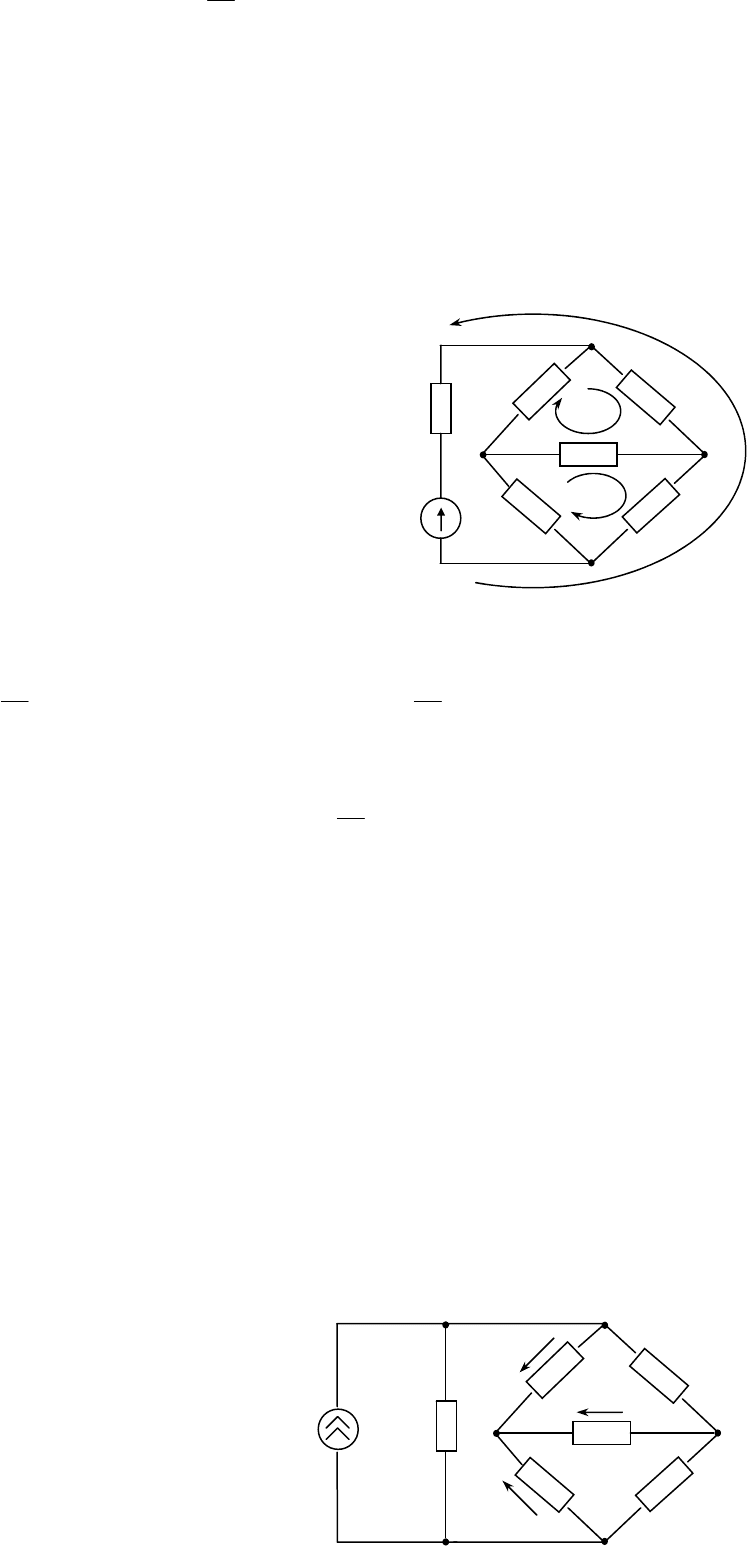
В мостовой схеме, представленной на рис.2.6, заданы все сопротивления и э.д.с.
E
.
Требуется определить ток
5
I
в ветви
5
R
(ток в диагонали мостовой схемы).
Схема содержит четыре узла и шесть ветвей. Следовательно, могут быть составлены три
уравнения по первому закону Кирхгофа и три уравнения по второму закону Кирхгофа:
.
ABCA контура для
;0
BCDB контура для
;0
ABDA контура для
;0
C узла для
;0
B узла для
;0
A узла для
663322
664433
552211
643
532
621
EIRIRIR
IRIRIR
IRIRIR
III
III
III
=++
=+−
=−+−
=−+
=+−
=+−−
В полученной системе шести уравнений неизвестными являются токи в ветвях. Решая
систему уравнений относительно искомого тока, находим:
2
I
1
R
2
R
3
R
4
R
5
R
6
R
E
1
I
3
I
4
I
5
I
6
I
A
B
C
D
2.6 Рис.
26
()()( )
[]
()
()()()
.R
где
),(
432164132
32414321632415
31425
RRRRRRRR
RRRRRRRRRRRRRRM
RRRR
M
E
I
+++++
+++++++++=
−=
Полученное выражение показывает, что ток в диагонали равен нулю, если выполнено
условие
4231
RRRR
= (условие равновесия мостовой схемы).
2.5.2 Расчет методом контурных токов
Пользуясь методом контурных токов, требуется определить ток в диагонали мостовой
схемы рис.2.7.
Выбранные положительные направле-
ния контурных токов
332211
и ,
III
указаны на
схеме стрелками. Число уравнений, записы-
ваемых по второму закону Кирхгофа, равно
трем (по числу независимых контуров):
()
()
()
.
;0
;0
33632223112
33322543115
33222511321
EIRRRIRIR
IRIRRRIR
IRIRIRRR
−=+++−−
=−+++−
=
−−++
Решение полученной системы уравне-
ний относительно контурных токов
2211
и
II
дает:
Рис.2.7
()
[]
()
[]
,;
521522254325311
RRRRRR
M
E
IRRRRRR
M
E
I +++−=+++−=
где M имеет то же значение, что и в предыдущем примере 2.5.1.
Искомый ток в диагонали мостовой схемы равен разности контурных токов:
()
,
314211225
RRRR
M
E
III −=−=
что совпадает с полученным в примере 2.5.1 ответом.
Если в заданной схеме контуры выбрать так, чтобы через ветвь
5
R
проходил только
один контурный ток, то искомый ток в ветви
5
R
будет равен именно этому контурному току,
то есть задача сведется к нахождению только одного контурного тока (вместо двух).
2.5.3 Расчет методом узловых потенциалов
Пользуясь методом узловых потенциалов, требуется определить ток в диагонали
мостовой схемы (см. рис.2.7).
В результате замены заданного источника напряжения эквивалентным источником
тока получится схема (рис.2.8), содержащая четыре узла. Для этой схемы по первому закону
Кирхгофа записывают
4-1=3
уравнения (по числу независимых узлов). Если выбрать в
данной схеме в качестве базиса узел 4 и направить токи в ветвях к базису, то уравнения
примут вид:
11
I
22
I
33
I
1
R
2
R
3
R
4
R
5
R
6
R
E
1
R
2
R
3
R
4
R
5
R
6
R
6
EGI
=
1
2
3
4
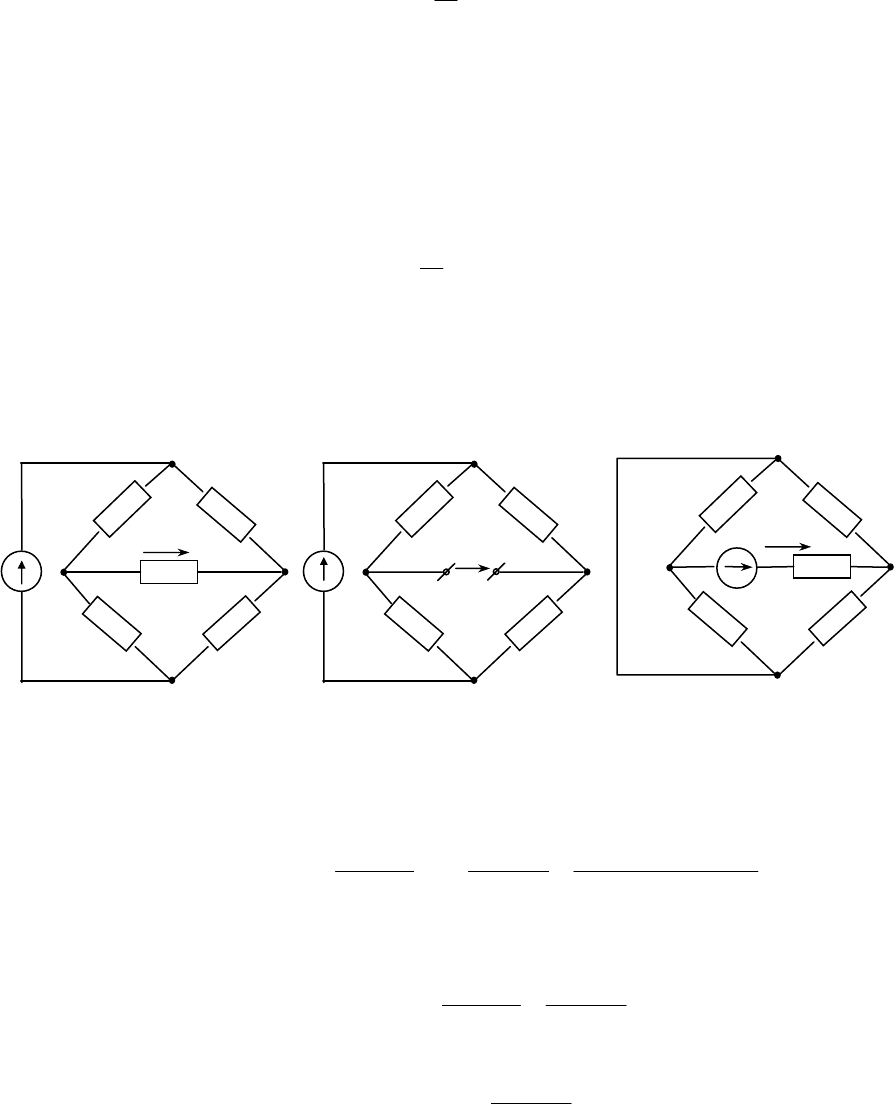
27
()
()
()
.
3 узла для
;0
2 узла для
;
1 узла для
636432316
33253212
636221621
EGGGGGG
GGGGG
EGGGGGG
−=+++−−
=−+++−
=−−++
ϕϕϕ
ϕϕϕ
ϕϕϕ
Рис.2.8
Решение полученной системы уравнений относительно
2
ϕ
даст:
()
,
314262
GGGGG
N
E
−=
ϕ
()()( )
[]
()
()()()
.
где
324164132
3241421643215
GGGGGGGGG
GGGGGGGGGGGGGN
+++++
++++++++=
Умножив найденный узловой потенциал
2
ϕ
на проводимость
5
G
диагональной ветви
мостовой схемы и изменив знак в соответствии с выбранным ранее направлением тока
5
I
(см. рис.2.6), найдем искомый ток:
()
.
4231655
GGGGGG
N
E
I −=
2.5.4 Расчет методом эквивалентного генератора
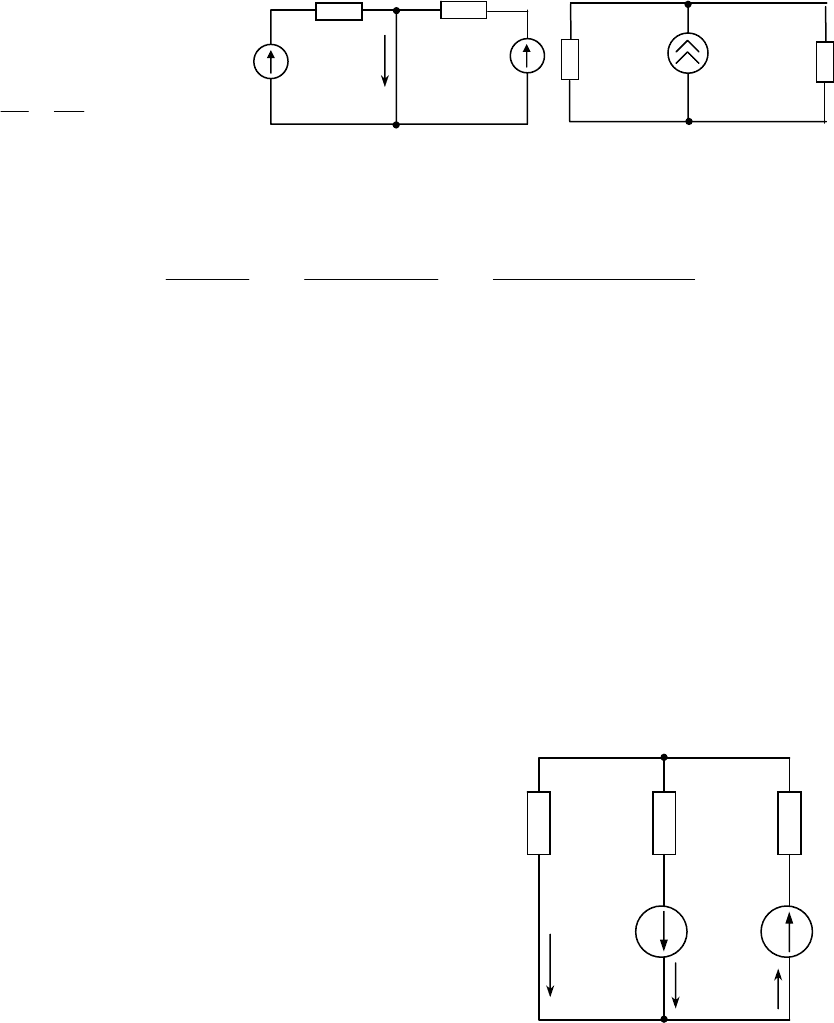
Пользуясь теоремой об эквивалентном источнике напряжения, определить ток в
диагональной ветви мостовой схемы рис.2.9а.
Рис.2.9а Рис.2.9б Рис.2.9в
Разомкнув ветвь
5
R , находим напряжение холостого хода
mn
U как разность
напряжений на участках
34
и RR (рис.2.9б):
()()
.
3241
3142
32
3
41
4
E
RRRR
RRRR
RR
E
R
RR
E
RU
mn
++
−
=
+
−
+
=
Сопротивление между зажимами m и n при E=0 и разомкнутой ветви
5
R равно
(рис.2.9в):
.
32
32
41
41
0
RR
RR
RR
RR
R
+
+
+
=
Тогда на основании метода эквивалентного генератора:
.
50
5
RR
U
I
mn
+
=
1
R
2
R
3
R
4
R
5
R
E
5
I
mn
U
m
1
R
2
R
3
R
4
R
E
n
5
R
5
I
mn
U
1
R
2
R
3
R
4
R
28
Пользуясь теоремой об эквивалентном источнике тока, определить ток
3
I в ветви
3
R
схемы рис.2.1.
Ток эквивалентного источ-
ника равен току короткого замы-
кания (
3
R =0, рис.2.10а):
.
2211
21
1
EGEG
R
E
R
E
II
кmn
+=+==
Рис.2.10а Рис.2.10б
Проводимость эквивалентного источника равна
210
GGG
+
=
. Следовательно, на
основании метода эквивалентного генератора искомый ток равен:
.
133221
2112
321
3
30
3
3
RRRRRR
ERER
I
GGG
G
I
GG
G
I
КК
++
+
=
++
=
+
=
2.6 БАЛАНС МОЩНОСТИ В ЦЕПЯХ ПОСТОЯННОГО ТОКА
При протекании тока по элементам электрической цепи имеет место безвозвратное
превращение энергии источников в другие виды энергии (тепловую, механическую,
световую и т.д.). При этом согласно закону сохранения энергии, работа и мощность
источников электрической энергии какой-либо цепи должна равняться работе и мощности
всех потребителей этой цепи.
Например, для цепи, представленной
на рис.2.11, уравнение баланса мощностей будет
иметь вид:
.
3
2
32
2
21
2
13322
RIRIRIIEIE ++++
В левой части уравнения баланса мощностей
стоит сумма мощностей, отдаваемых источниками
э.д.с. Правая часть уравнения представляет собой
сумму мощностей отдельных приемников. При
подсчете баланса мощностей в ряде случаев может
оказаться, что мощность, отдаваемая источником
электрической энергии, отрицательна. Это будет иметь
место в тех случаях, когда э.д.с.
E и ток I источника
направлены противоположно. В этом случае источник
работает в режиме потребителя. Примером такого
режима работы источника может служить процесс
зарядки аккумуляторных батарей.
Рис.2.11
В теории электрических цепей баланс мощностей может использоваться для проверки
правильности определения токов. Действительно, уравнение баланса мощностей для цепи
будет выполняться только при условии точного расчета токов в этой цепи.
2.7 КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ ПО МОДУЛЮ 2
1. Пояснить целесообразность применения различных методов расчета электрических цепей
к схемам разной конфигурации.
2.
Проиллюстрировать на примере практическую целесообразность применения теоремы об
эквивалентном источнике тока и напряжения.
1
E
2
E
1
R
2
R
К
I
К
I
3
R
0
R
2
R
1
R
3
R
3
E
2
E
1
I
2
I
3
I
29
3. Как определяется проводимость узла и общая проводимость между узлами при
использовании метода узловых потенциалов?
4.
Почему потенциал базисного узла можно приравнять к нулю?
5.
Почему метод эквивалентного генератора часто называют методом холостого хода и
короткого замыкания?
Выполнить лабораторные работы по темам «Метод контурных
токов», «Метод узловых потенциалов» и «Метод эквивалентного
генератора», используя соответствующие моделирующие программы.
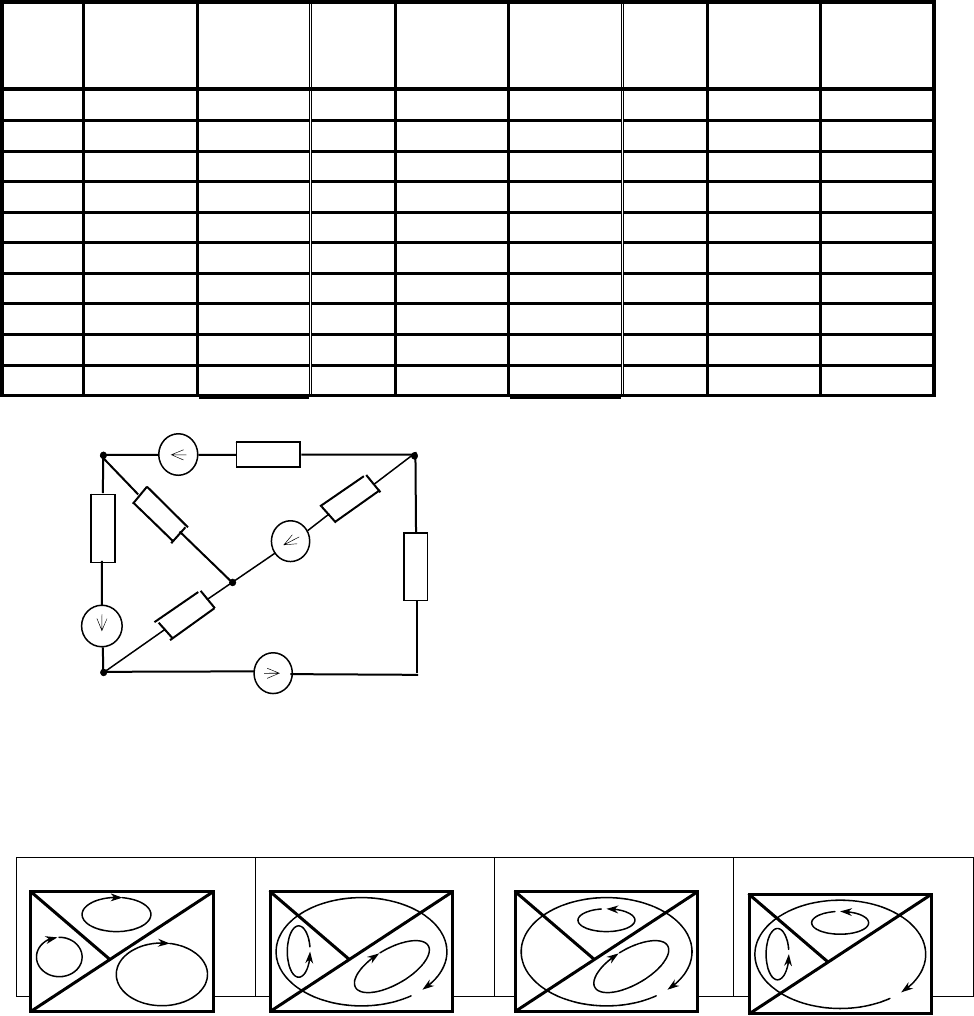
Задания для расчетной работы по теме «Метод контурных токов».
Определить значения контурных токов, составив систему уравнений по методу
контурных токов, определить все токи в ветвях и составить баланс мощностей для всей
электрической цепи.
Схема и контуры, для которых необходимо составить уравнения, определяются в
соответствие с выданным вариантом. Для расчета использовать моделирующую программу.
Ва-
риант
Рисунок
схемы
Контуры Ва-
риант
Рисунок
схемы
Контуры Ва-
риант
Рисунок
схемы
Контуры
1 1 1.1 11 1 1.11 21 3 3.1
2 1 1.2 12 1 1.12 22 3 3.2
3 1 1.3 13 2 2.1 23 3 3.3
4 1 1.4 14 2 2.2 24 3 3.4
5 1 1.5 15 2 2.3 25 3 3.5
6 1 1.6 16 2 2.4 26 3 3.6
7 1 1.7 17 2 2.5 27 3 3.7
8 1 1.8 18 2 2.6 28 3 3.8
9 1 1.9 19 2 2.7 29
10 1 1.10 20 2 2.8 30
Схема 1
Дано:
=
1
E 3 В
=
2
E 4 В
=
3
E 5 В
=
4
E
3 А
=
1
R 2 Ом
=
2
R 1 Ом
=
3
R 6 Ом
=
4
R
2 Ом
=
5
R 10 Ом
=
6
R 3 Ом
Варианты контуров для схемы 1.
E
1
E
4
1
3
4
R
1
R
4
R
6
E
3
R
2
2
R
5
R
3
E
2
30
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
1.10
1.11
1.12
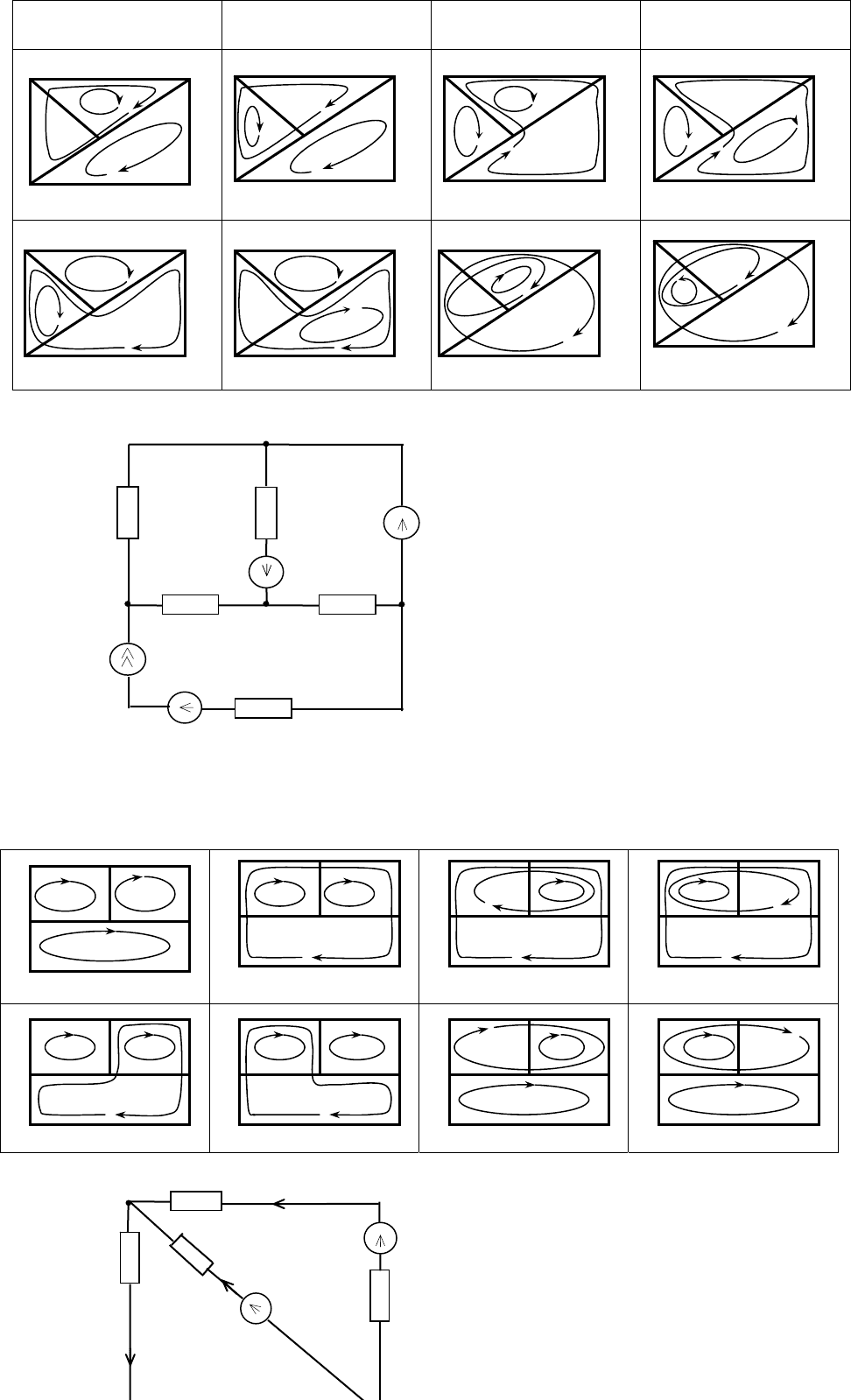
Схема 2
Дано:
=
1
E 25 В
=
2
E 10 В
=
6
E 20 В
=
J 2 А
=
2
R 10 Ом
=
3
R 20 Ом
=
4
R
10 Ом
=
5
R 8 Ом
=
6
R 5 Ом
Варианты контуров для схемы 2.
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
Дано:
=
1
E 2 В
=
2
E
3 В
=
3
E 2 В
1
4
3
2
R
5
R
6
R
4
R
3
R
2
J
E
2
E
1
E
6
3
R
1
R
5
E
1
R
2
E
2
R
3
I
1
I
3
