Лукоянычев В.Г. Электротехника
Подождите немного. Документ загружается.

31
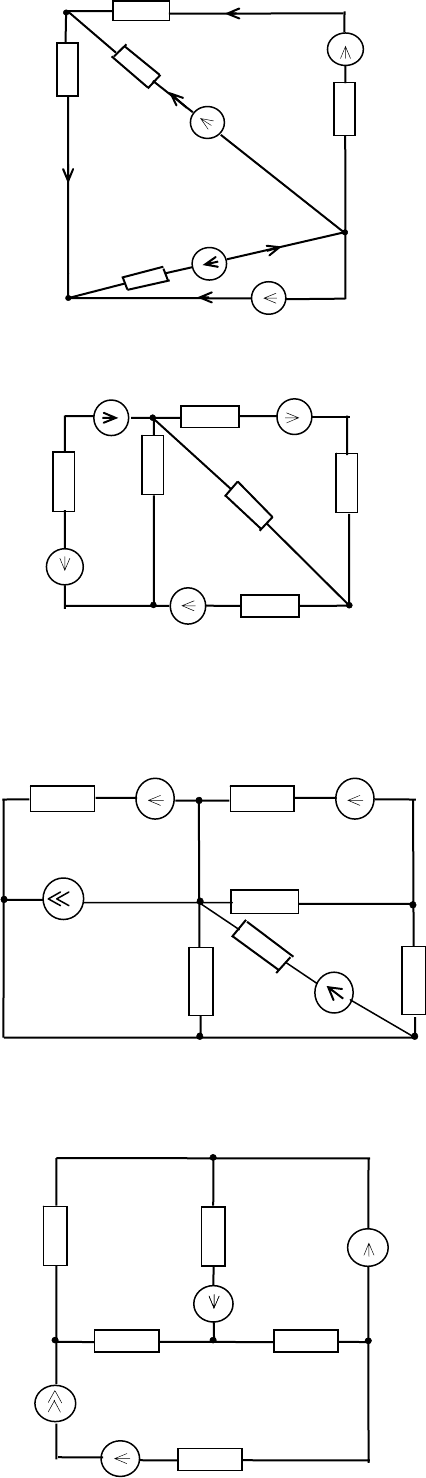
Схема 3
=
4
E
4 В
=
1
R 1 Ом
=
2
R 2 Ом
=
3
R 3 Ом
=
4
R
2 Ом
=
5
R 3 Ом
Варианты контуров для схемы 3.
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
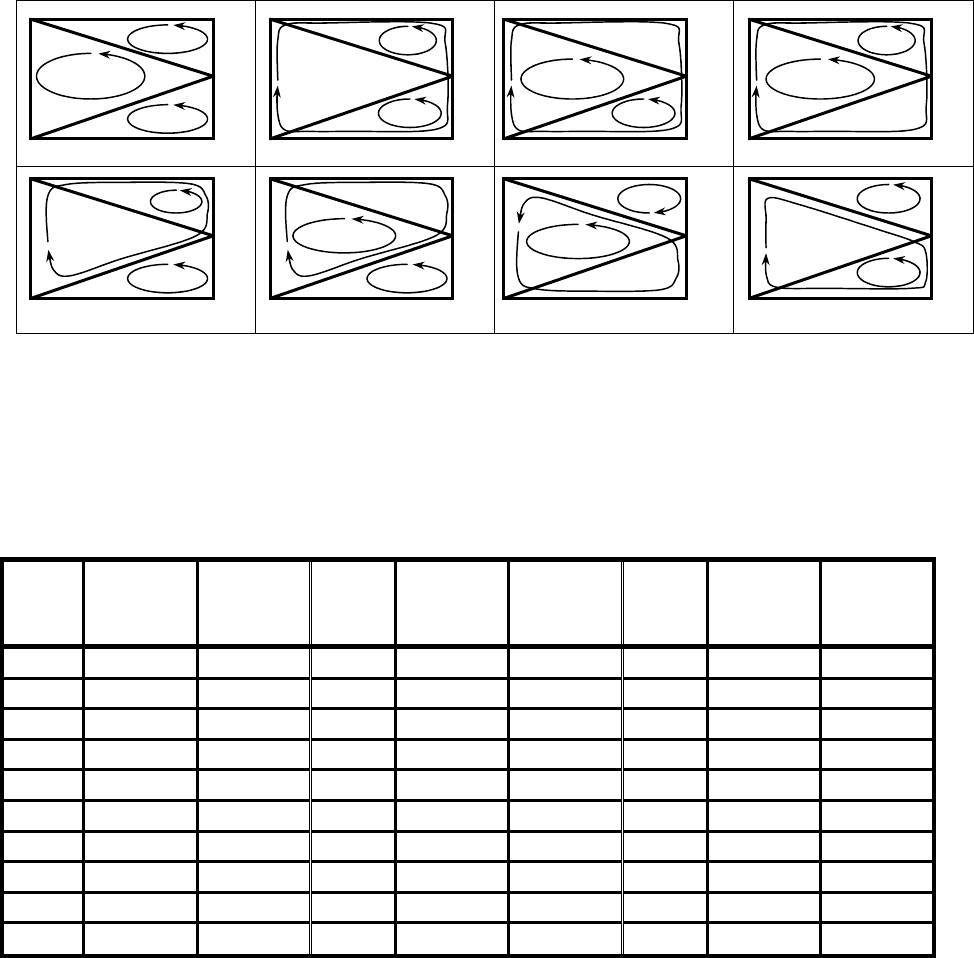
Задания для расчетной работы по теме «Метод узловых потенциалов».
Определить значения потенциалов узлов, составив систему уравнений по методу
узловых потенциалов, и определить все токи в ветвях.
Схема и базисный узел (номер узла) определяется в соответствие с выданным
вариантом. Для расчета использовать моделирующую программу.
Ва-
риант
Рисунок
схемы
Базис-
ный
узел
Ва-
риант
Рисунок
схемы
Базис-
ный
узел
Ва-
риант
Рисунок
схемы
Базис-
ный
узел
1 1 1 11 4 2 21 4 4
2 1 2 12 4 3 22 7 1
3 1 3 13 6 1 23 7 2
4 2 1 14 6 2 24 7 3
5 2 2 15 6 3 25 7 4
6 2 3 16 6 4 26
7 3 1 17 5 1 27
8 3 2 18 5 2 28
9 3 3 19 5 3 29
10 4 1 20 5 4 30
32
Схема 1
Дано:
=
1
E
2 В
=
2
E 3 В
=
3
E 2 В
=
4
E 4 В
=
1
R
1 Ом
=
2
R 2 Ом
=
3
R 3 Ом
=
4
R 2 Ом
=
5
R 3 Ом
Схема 2
Дано:
=
1
E
2 В
=
2
E 20 В
=
3
E 6 В
=
4
E 4 В
=
1
R
2 Ом
=
2
R 10 Ом
=
3
R 4 Ом
=
4
R 1 Ом
=
5
R 3 Ом
=
6
R 4 Ом
Схема 3
Дано:
=
1
E
4 В
=
2
E 3 В
=
3
E 5 В
=
4
J 8 А
=
1
R
2 Ом
=
2
R 1 Ом
=
3
R 0.5 Ом
=
4
R 2 Ом
=
5
R 0.2 Ом
=
6
R 5 Ом
Дано:
=
1
E 25 В
=
2
E 10 В
=
6
E 20 В
=
J
2 А
=
2
R 10 Ом
=
3
R 20 Ом
=
4
R 10 Ом
=
5
R 8 Ом
=
6
R 5 Ом
R
5
3
R
6
J
4
E
1
R
1
E
2
R
2
R
4
R
3
E
3
1
2
E
2
E
4
1
3
2
R
1
R
5
R
2
R
6
R
4
E
3
E
1
R
3
1
4
3
2
R
5
R
6
R
4
R
3
R
2
J
E
2
E
1
E
6
E
4
1
3
R
1
R
4
R
5
E
1
R
2
2
E
2
R
3
E
3
I
4
I
1
I
3
I
5
33
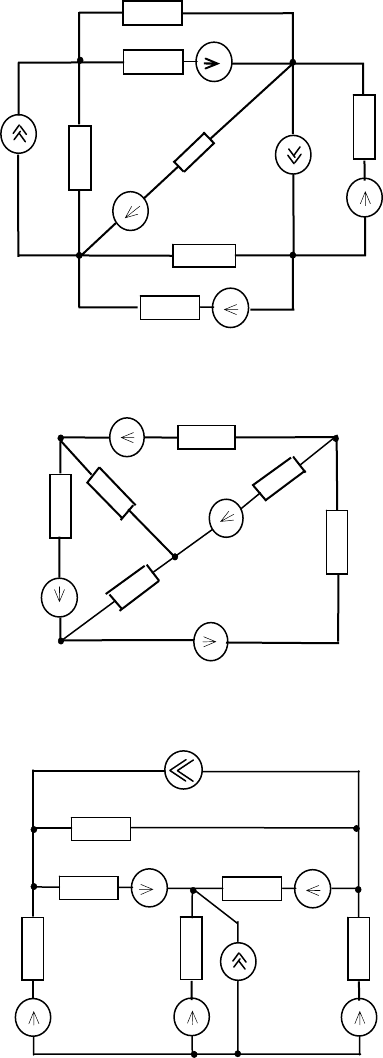
Схема 4
Схема 5
Дано:
=
1
E
3 В
=
2
E 4 В
=
3
E 12 В
=
4
E 10 В
=
1
J
7 A
=
2
J 8 A
=
1
R
0.25 Ом
=
2
R 0.4 Ом
=
3
R 1 Ом
=
4
R 2.5 Ом
=
5
R 2 Ом
=
6
R 0.5 Ом
=
7
R 1.25 Ом
Схема 6
Дано:
=
1
E
3 В
=
2
E 4 В
=
3
E 5 В
=
4
E 3 А
=
1
R
2 Ом
=
2
R 1 Ом
=
3
R 6 Ом
=
4
R 2 Ом
=
5
R 10 Ом
=
6
R 3 Ом
Схема 7
Дано:
=
1
E
4 В
=
2
E 5 В
=
3
E 2 В
=
4
E 10 В
=
5
E 1 В
=
1
J
3 A
=
2
J 3 A
=
1
R
2 Ом
=
2
R 1 Ом
=
3
R 0.25 Ом
=
4
R 5 Ом
=
5
R 0.5 Ом
=
6
R 0.5 Ом
1
3
2
R
6
J
2
E
1
R
1
E
2
R
2
E
4
R
4
E
5
R
5
E
3
R
3
J
1
4
R
3
3
R
7
E
4
J
2
1
R
5
J
1
2
E
1
E
1
R
1
R
4
4
E
2
R
2
R
6
E
1
E
4
1
3
4
R
1
R
4
R
6
E
3
R
2
2
R
5
R
3
E
2
34
3 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО
СИНУСОИДАЛЬНОГО ТОКА
3.1 СИНУСОИДАЛЬНЫЕ ЭЛЕКТРИЧЕСКИЕ ВЕЛИЧИНЫ
Электромагнитный процесс в электрической цепи, при котором мгновенные значения
напряжений и токов повторяются через равные промежутки времени, называется
периодическим. Наименьшее время, по истечении которого мгновенные значения
периодической величины повторяются, называется периодом. Если величину, являющуюся
периодической функцией времени t, обозначить через F(t), то для любого положительного
или отрицательного значения аргумента t справедливо равенство
(
)
(
)
период. - T где ,tFTtF
=
±
Геометрически это значит, что ординаты двух произвольных точек графика F(t) с
абсциссами, различающимися на T, одинаковы.
Величина, обратная периоду, то есть число периодов в единицу времени, называется
частотой:
.
1
T
f =
Частота имеет размерность 1/сек, а единицей измерения частоты служит герц (Гц);
частота равна 1 Гц, если период равен 1 сек.
Преобладающим видом периодического процесса в электрических цепях является
синусоидальный режим, характеризующийся тем, что все напряжения и токи являются
синусоидальными функциями одинаковой частоты. Это возможно только при заданных
синусоидальных э.д
.с. и токах источников. Тем самым обеспечивается наиболее выгодный
эксплуатационный режим работы электрических установок.
Из курса математического анализа известно, что синусоида является простейшей
периодической функцией; всякие другие несинусоидальные периодические функции могут
быть разложены в бесконечный ряд синусоид, имеющих кратные частоты. Поэтому для
исследования процессов в цепях переменного тока в первую
очередь необходимо изучить
особенности цепей синусоидального тока.
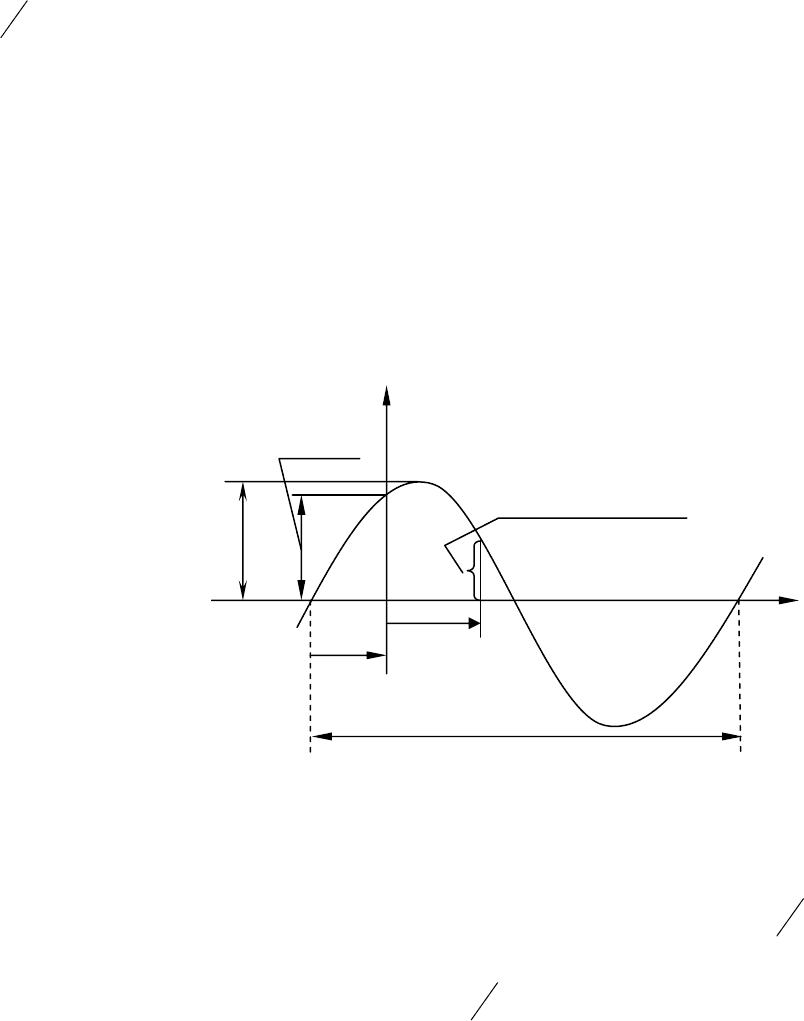
На рис.3.1 изображена
синусоидальная функция
);sin(
ψ
ω
+
= tUu
m
где
m
U - максимальное значение,
или амплитуда;
ω
- скорость
изменения аргумента (угла),
называемая угловой частотой;
она равна произведению частоты
на
π
2
:
;/,2 секрадf
π
ω
=
Ψ- начальная фаза, определяемая
величиной смещения синусоиды
относительно начала координат;
она измеряется абсциссой точки
перехода отрицательной полу-
волны в положительную.
Рис.3.1
Начальная фаза ψ представляет собой алгебраическую величину. Угол ψ
положителен и отсчитывается вправо, к точке t=0, когда синусоидальная функция смещена
влево относительно начала координат (рис.3.1).
Косинусоида может рассматриваться как синусоида с начальной фазой
2
π
ψ
= .
Если функция задана в косинусоидальной форме ),cos(
1
ψ
ω
+
=
tUu
m
то она может быть
приведена к синусоидальной форме путем замены
.
2
1
π
ψψ
−=
0
ψ
sin
m
U
m
U
U
()
ψ
ω
+
=
tUu
m
sin
π
2
0>
ψ
t
ω
t
ω
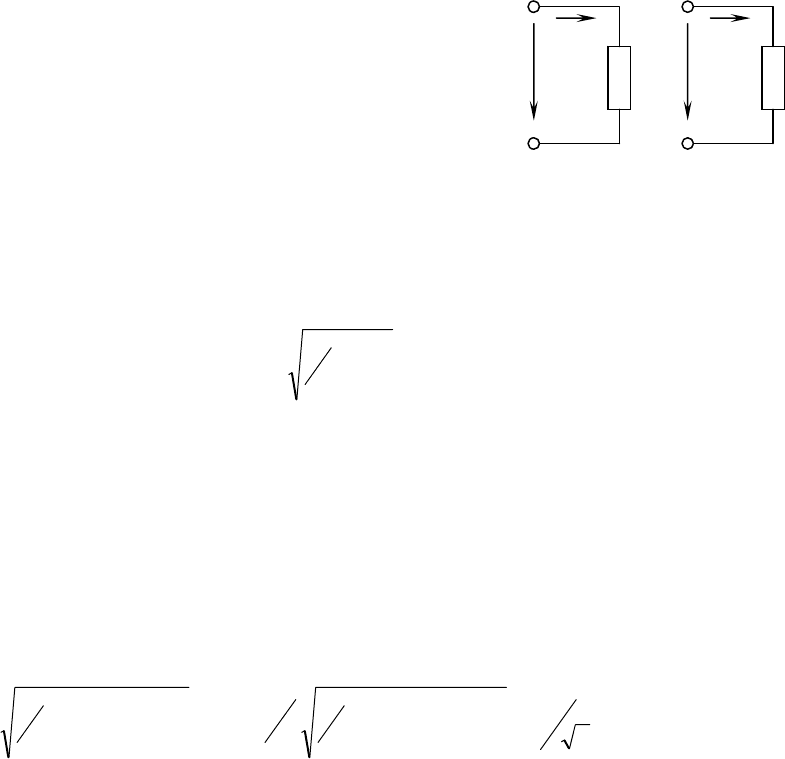
35
За аргумент функции может быть принято время t или соответственно угол ωt.
Аргументу t соответствует период T, а аргументу ωt – период ωT=2π. Следует иметь в виду,
что аргумент ωt измеряется в радианах, причем в тех же единицах измеряется и начальная
фаза.
Если угол ψ вычисляется в градусах, то аргумент
ωt также переводится в градусы;
в этом случае период составляет 360
o
.
Величина ωt+ψ, определяющая стадию изменения синусоидальной величины,
называется фазовым углом или фазой. С течением времени фаза возрастает, причем после
увеличения на 2π цикл изменения синусоидальной величины повторяется.
3.2 ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ СИНУСОИДАЛЬНОГО ТОКА
В электротехнике при расчете цепей переменного тока чаще всего интересуются не
величиной тока или напряжения в данный момент времени, а его тепловым или
электромеханическим действием.
Тепловое действие тока, а также механическая сила взаимодействия двух
проводников, по которым проходит один и тот же ток, пропорционально квадрату тока.
Поэтому о величине тока судят
обычно по так называемому действующему значению за
период.
Сравним переменный ток с постоянным по тепловому действию. Пусть имеются цепи
переменного и постоянного тока, причем в обоих случаях напряжение приложено к
резисторам с равным по величине сопротивлением (рис.3.2) Подсчитаем количество тепла A,
выделяющегося в цепи переменного тока за время одного периода. Формулу
закона Джоуля-
Ленца для подсчета количества тепла в том виде, как она записана для постоянного тока,
применять нельзя. Однако для бесконечно малого промежутка времени эта формула
применима, так как в течение времени dt ток можно считать неизменным:
.
2
RdtidA =
Для подсчета количества тепла за период нужно про-
интегрировать предыдущее выражение:
.
2
0
dtiRA
T
∫
=
Подсчитаем количество тепла, выделяющегося в цепи
постоянного тока за время, равное одному периоду
переменного тока:
.
2
RTIA =
Рис.3.2
Для того, чтобы сравнить переменный ток с постоянным по тепловому действию,
приравняем выражения :
.
2
0
2
RTIdtiR
T
=
∫
Из последнего выражения находим связь между постоянным и переменным токами:
∫
=
T
dti
T
I
0
2
1
.
Значение переменного тока, определяемое как среднее квадратичное значение за
период, и называется действующим током. Это равенство показывает, что действующее
значение периодического тока равно по величине такому постоянному току, который,
проходя через неизменное сопротивление R, за период времени T выделяет то же количество
тепла, что и данный ток I. Последнее выражение
является общим для подсчета
действующего тока, изменяющегося по любому периодическому закону. Аналогично
определяются действующие периодические напряжения, э.д.с., магнитный поток и т.д.
Действующий ток обозначается прописной буквой без индексов, то есть так же, как и
постоянный ток. Найдем связь между действующим током и амплитудным значением
синусоидального тока:
.707,0
2
)2cos1(
1
2
sin
1
00
22
m
m
T
m
T
m
I
I
dtt
T
I
dttI
T
I ⋅≈=−==
∫∫
ωω
R
I
U
i
u
R

36
Аналогично определяется связь между действующим и амплитудным значениями
переменного синусоидального напряжения:
.707,0
2
1
0
2
m
m
T
U
U
dtu
T
U ≈==
∫
Амперметры и вольтметры переменного тока, как правило, градуируются в
действующих значениях токов и напряжений. Действующими значениями обычно
пользуются и при расчетах электрических цепей переменного тока.
3.3 ИЗОБРАЖЕНИЕ СИНУСОИДАЛЬНЫХ ФУНКЦИЙ
ВРАЩАЮЩИМИСЯ ВЕКТОРАМИ
Синусоидальные функции времени могут быть изображены в виде временных графиков
или условно с помощью вращающихся векторов. Изображение синусоидальных функций
времени в виде графиков не всегда удобно. Например, при рассмотрении цепей переменного
тока приходится встречаться со сложными синусоидальными источниками э.д.с. или токов
одной и той же частоты, имеющих различные амплитуды
и различные начальные фазы.
Суммирование синусоидальных функций выполняется проще, если они представлены не в
виде графиков, а в виде вращающихся векторов. В последнем случае суммирование
синусоидальных функций сводится к операции сложения векторов. Кроме того, изображение
синусоидальных функций вращающимися векторами дает более наглядное представление о
фазовых соотношениях в цепях переменного тока.
Рассмотрим способ изображения синусоидальных функций вращающимися
векторами на частном примере. Пусть, например, требуется представить ток
)sin(
im
tIi
ψ
ω
+= в виде вращающегося вектора. С этой целью возьмем вектор 0В, равный
по модулю амплитуде тока
m
I , и расположим его под углом
i
ψ
к горизонтальной линии 0x.
Положительные углы условимся отсчитывать от горизонтальной линии 0х против часовой
стрелки. Способ условного изображения синусоидального тока посредством вращающегося
вектора представлен на рис.3.3. Из рис.3.3 следует, что проекция вектора 0В на
вертикальную ось 0у равна мгновенному току ,sin
im
Ii
ψ
=
соответствующему моменту
времени t=0. Для получения мгновенного тока в какой-либо другой момент времени,
например
1
t , следует повернуть вектор 0В на угол ω
1
t против часовой стрелки и определить
проекцию векторов 0В на вертикальную ось 0у (рис.3.3). Эта проекция равна 0М, то есть
равна мгновенному току в момент времени
1
tt
=
:
).sin(
1
1
imt
tIi
ψ
ω
+
=
Совокупность векторов, представляющих токи или напряжения или то и другое,
называется векторной диаграммой.
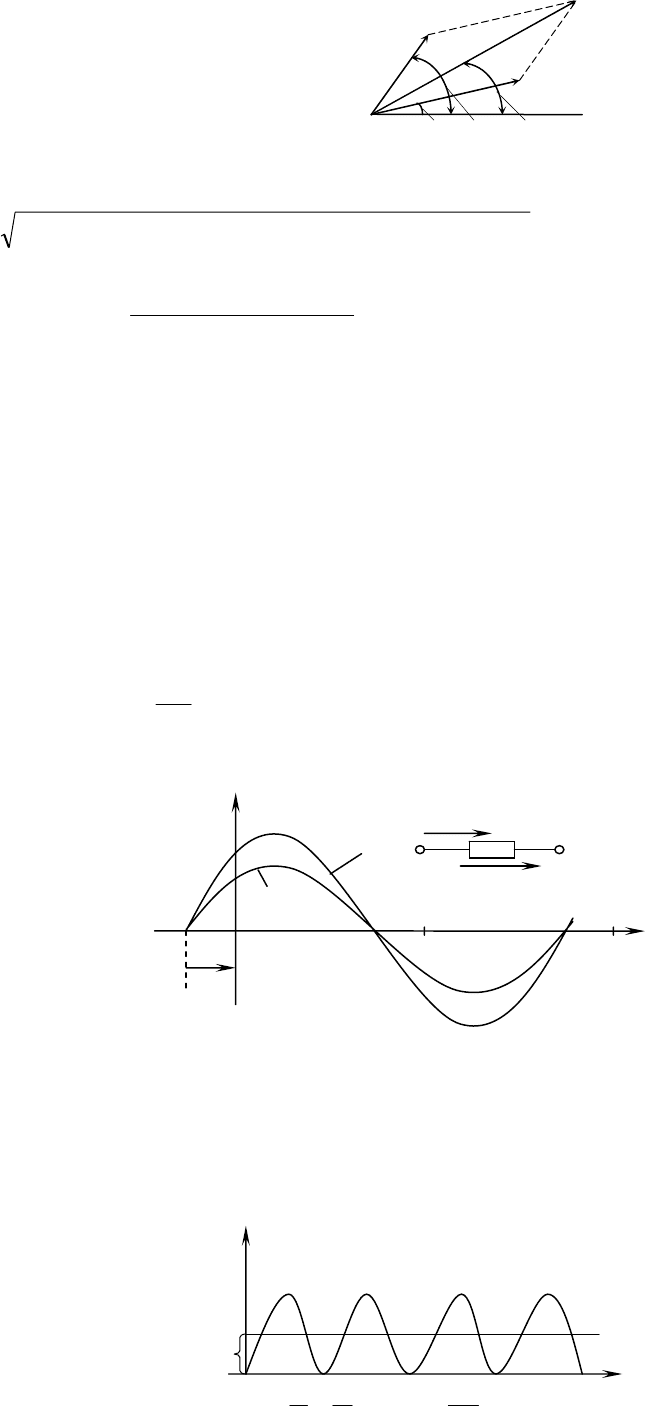
Рассмотрим операцию суммирования двух синусоидальных токов, имеющих
одинаковые частоты, с использованием векторной диаграммы. Просуммируем токи (рис.3.4):
).sin();sin(
222111
ψ
ω
ψ
ω
+
=
+
= tIitIi
mm
Изобразим ток
1
i вектором 0В, имеющим в выбранном масштабе длину
1m
I и
повернутым относительно горизонтальной оси 0х на угол
1
ψ
против хода часовой стрелки.
im
I
ψ
sin
0
i
ψ
m
I
B
M
x
y
i
t
ω
m
I
i
ψ
0
1
t
ω
(
)
im
tIi
ψ
ω
+
=
sin
Рис.3.3
37
Ток
2
i
изобразим в том же масштабе векторов 0С,
имеющим длину
2m
I и повернутым относительно оси 0х
против хода часовой стрелки на угол
2
ψ
.
Просуммировав векторы 0В и 0С, получим вектор
0К, условно изображающий суммарный ток
)sin(
21
ψ
ω
+
=+= tIiii
m
в момент времени t=0.
Рис.3.4
Длина вектора 0К определяется на основании теоремы Пифагора:
()()
.sinsincoscos0
2
2211
2
2211
ψψψψ
mmmmm
IIIIIK +++==
Начальная фаза ψ результирующего вектора 0К находится из выражения
.
coscos
sinsin
2211
2211
ψψ
ψ
ψ
ψ
mm
mm
II
II
tg
+
+
=
Для получения мгновенного значения суммарного тока i в какой-либо момент
времени
1
t
нужно повернуть вектор 0К на дополнительный угол
1
t
ω
против хода часовой
стрелки и спроецировать его на вертикальную ось.
Следует помнить, что ток и напряжение являются величинами скалярными.
Изображение токов и напряжений вращающимися векторами есть чисто формальный
математический прием, позволяющий условно отобразить синусоидальные функции.
Вращающиеся вектора являются математическими векторами в отличии от физических
векторов, имеющих определенное направление в пространстве.
3.4 СИНУСОИДАЛЬНЫЙ ТОК В СОПРОТИВЛЕНИИ
Если синусоидальное напряжение )sin(
ψ
ω
+
=
tUu
m
подвести к сопротивлению r, то
через сопротивление пройдет ток
).sin()sin(
ψωψω
+=+= tIt
r
U
i
m
m
Следовательно,
напряжение на зажимах сопротивления и ток, проходящий через это сопротивление, имеют
одинаковую начальную фазу и совпадают по фазе. Они одновременно достига-
ют своих амплитудных значений
mm
IU и
и, соответственно, одновременно прохо-
дят через нуль (рис.3.5).
Разность начальных фаз двух синусоид,
имеющих одинаковую частоту,
называется фазовым сдвигом. В данном
случае фазовый сдвиг между
напряжением u и током i равен нулю:
.0=−=
iu
ψ
ψ
ϕ
Рис.3.5
При прохождении синусоидального тока через сопротивление r не только мгновенные
значения напряжения на сопротивлении и тока в нем, но и амплитуды и, соответственно,
действующие значения напряжения и тока связаны законом Ома:.; rIUrIU
mm
==
Мгновенная мощность, поступающая в сопротивление:
[
]
,)(2cos1)(sin
2
ψωψω
+−=+== tUItIUiup
mmr
изменяется с угловой частотой, удвоенной по
сравнению с частотой напряжения и тока, и
колеблется в пределах от 0 до 2UI (рис.3.6).
Как видно из формулы мгновенной
мощности, кривая
r
p
состоит из двух
слагающих: постоянной слагающей UI и
косинусоидальной функции, имеющей
амплитуду UI и угловую частоту 2ω.
Рис.3.6
K
x
1
ψ
2
ψ
ψ
1m
I
2m
I
m
I
0
C
B
0
0>
ψ
i
u
0
=
ϕ
ui,
t
ω
π
2
π
i
u
r
p
P
0
r
p
t
ω
π
=
2
T
ω
π
2
=T
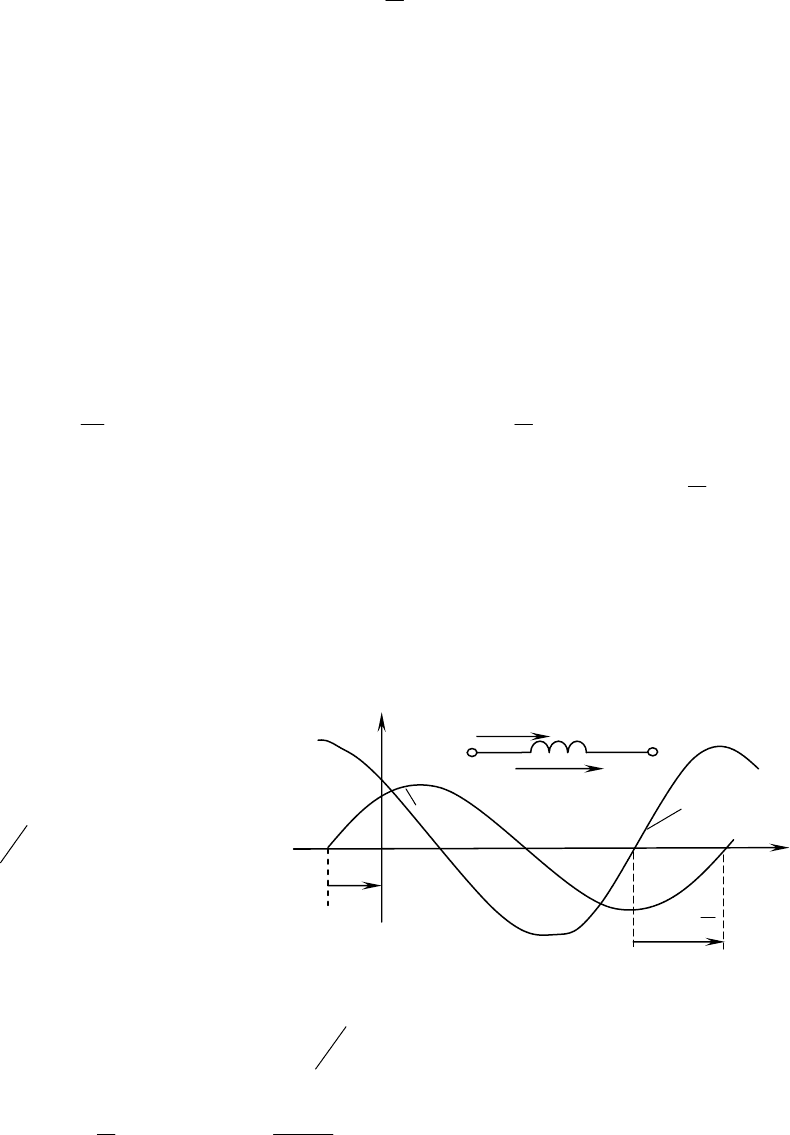
38
Ввиду того, что в рассматриваемом случае напряжение и ток совпадают по фазе, то есть
всегда имеют одинаковый знак (плюс или минус), их произведение всегда положительно.
Среднее значение мощности за период
∫
=
T
r
dtp
T
P
0
1
называется активной мощностью
и измеряется в ваттах. Активная мощность равна: P=UI=r
2
I
. Сопротивление r может быть
определено как отношение активной мощности к квадрату действующего значения тока:
./
2
IPr =
Сопротивление проводника при переменном токе больше, чем при постоянном токе,
вследствие явлений поверхностного эффекта, возникновения вихревых токов и излучения
электромагнитной энергии в пространство (при высоких частотах). В отличие от
сопротивления при постоянном токе сопротивление проводника при переменном токе
называется активным сопротивлением.
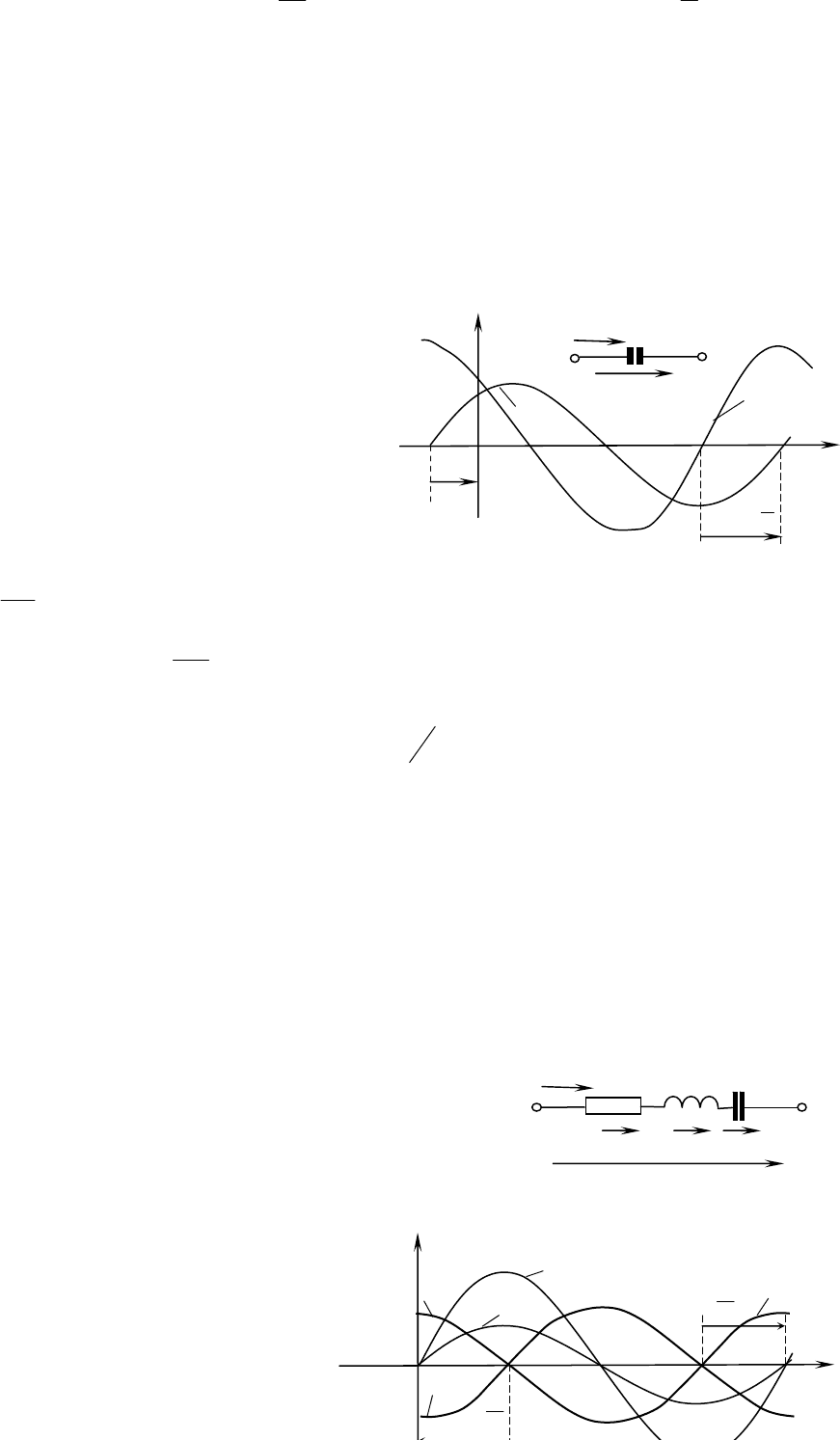
3.5 СИНУСОИДАЛЬНЫЙ ТОК В ИНДУКТИВНОСТИ
Пусть через индуктивность L проходит ток ).sin(
ψ
ω
+
=
tIi
m
Электродвижущая сила самоиндукции определяется по формуле:
).
2
sin()cos(
π
ψωψωω
++−=+−=−= tUtLI
dt
di
Le
mmL
Следовательно, напряжение на индуктивности
).
2
sin(
π
ψω
++=−= tUeu
mLL
Полученное выражение показывает, что напряжение на индуктивности опережает ток
на угол π/2: максимум напряжения смещен влево относительно максимума тока на π/2
(рис.3.7). Когда ток проходит через нуль, напряжение достигает положительного или
отрицательного максимума, так как оно пропорционально скорости изменения тока (di/dt),
которая в момент прохождения тока через нуль максимальна
(синусоида тока в этот момент
имеет наибольшую крутизну). Когда ток достигает максимума, скорость его изменения, а
следовательно, и напряжение на индуктивности обращается в нуль.
Под фазовым сдвигом φ тока
относительно напряжения понимается
разность начальных фаз напряжения и
тока. Следовательно, в данном случае
.
2
π
ψψϕ
=−=
iu
Амплитуда, так же как и действующие
значения напряжения и тока, связаны
соотношением, подобным закону Ома:
.; IxUIxLIU
LmLmm
===
ω
Рис.3.7
Величина ,Lx
L
ω
=
имеющая размерность сопротивления, называется индуктивным
сопротивлением; обратная ей величина
L
b
L
ω
1
=
называется индуктивной проводимостью.
Мгновенная мощность, поступающая в индуктивность, будет равна:
).(2sin)sin()cos(2
2
)sin()
2
sin(
ψωψωψωψω
π
ψω
+=+⋅+=+⋅++= tUItt
IU
ttIUp
mm
mmL
Она колеблется по синусоидальному закону с угловой частотой 2ω, имея амплитуду
UI. Мгновенная мощность в данном случае равна скорости изменения энергии магнитного
поля индуктивности.
Поступая от источника, энергия временно запасается в магнитном поле
индуктивности, затем возвращается в источник при исчезновении магнитного поля. Энергия
магнитного поля достигает максимума в момент перехода
тока в индуктивности через
амплитудное значение, затем она убывает и обращается в нуль при токе, равном нулю.
Таким образом, происходит колебание энергии между источником и индуктивностью,
причем активная мощность, поступающая в индуктивность, равна нулю.
i
u
L
ui,
0
0>
ψ
i
u
t
ω
2
π
ϕ
=
39
3.6 СИНУСОИДАЛЬНЫЙ ТОК В ЕМКОСТИ
Пусть напряжение на емкости синусоидально: )sin(
ψ
ω
+
=
tUu
m
.
Ток в емкости равен:
).
2
sin()cos(
π
ψωψωω
++=+== tItCU
dt
du
Ci
mm
Изменение электрического заряда происходит по синусоидальному закону в
соответствии с приложенным напряжением u. При этом попеременное накапливание
положительных и отрицательных электрических зарядов на пластинах емкости
обуславливается прохождением в цепи синусоидального тока i. Его величина определяется
скоростью изменения заряда на емкости (dq/dt).
Из выражения видно, что i опережает приложенное u на
угол π/2 (рис.3.8). Нулевым
значениям тока соответствуют максимальные (положительные и отрицательные) значения
напряжения. Физически это объясняется тем, что когда электрический заряд q и,
соответственно, напряжение u=q/C достигают максимального значения (положительного или
отрицательного), ток i равен нулю.
Под фазовым сдвигом тока относи-
тельно напряжения подразумевается разность
начальных фаз напряжения и тока,
то есть
.2/
π
ψ
ψ
ϕ
−=−=
iu
В отличие от цепи с ин-
дуктивностью, где φ= +π/2, фазовый сдвиг
тока относительно напряжения в случае ем-
кости отрицателен (φ= –π/2).
Амплитуды и, соответственно, действующие
значения напряжения и тока связаны
соотношением, подобным закону Ома:
.;
1
IxUIxI
C
U
CmCmm
===
ω
Рис.3.8
Величина ,
1
C
x
C
ω
=
имеющая размерность сопротивления, называется емкостным
сопротивлением. Мгновенная мощность, поступающая в емкость,
)(2sin)
2
sin()sin(
ψω
π
ψωψω
+=++⋅+== tUIttIUuip
mmc
колеблется синусоидально с угловой частотой 2ω, имея амплитуду, равную UI. Мгновенная
мощность, поступающая в емкость, равна скорости изменения энергии электрического поля
емкости. Поступая от источника, энергия временно запасается в электрическом поле
емкости, а затем возвращается в источник при исчезновении электрического поля. Энергия
электрического поля достигает максимума при амплитудном значении напряжения
на
емкости. Затем она убывает и обращается в нуль при напряжении, равном нулю.
Таким образом, так же как в случае индуктивности, происходит колебание энергии
между источником и емкостью, причем активная мощность равна нулю.
3.7 ЦЕПИ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
При прохождении синусоидального тока
tIi
m
ω
sin= через электрическую цепь, состоящую из
последовательно соединенных элементов r,L,C
(рис.3.9), на зажимах этой цепи создается
напряжение, равное алгебраической сумме
синусоидальных напряжений на отдельных
элементах (второй закон Кирхгофа): .
CLr
uuuu
+
+
=
Рис.3.9
Напряжение
r
u на сопро-
тивлении r совпадает по фазе с
током i, напряжение
L
u на индук-
0
ψ
i
u
ui,
t
ω
2
π
ϕ
=
i
u
C
i
r
u
C
u
L
r
L
u
C
u
C
u
0
CLr
uuu ,,
t
ω
r
u
L
u
2
π
−
i
2
π
L
u
40
тивности L опережает, а напряже-
ние
C
u на емкости C отстает по
фазе от i на π/2 (рис.3.10). Следо-
вательно, напряжение u на зажи-
мах всей цепи равно:
Рис.3.10
()
.
1
где ,cossin
cos
1
sincos
1
cossin)sin(
C
LxxxtxtrI
tI
C
LtrItI
C
tLItrItU
CLm
mmmmmm
ω
ωωω
ω
ω
ωωω
ω
ωωωψω
−=−=+
=
⎟
⎠
⎞
⎜
⎝
⎛
−+=−+=+
Величина x называется реактивным сопротивлением цепи, которое в зависимости от
знака может иметь индуктивный (x>0) или емкостной (x<0) характер.
В отличие от реактивного сопротивления x величина активного сопротивления r
всегда положительна.
Для нахождения
m
U и φ воспользуемся тригонометрическими соотношениями:
.);sin(cossin
22
m
n
arctgnmnm =±+=±
ϕϕααα
Тогда
.;
22
r
x
tgIxrU
mm
=+=
ϕ
Выражение для
m
U показывает, что амплитуда и действующие значения напряжения
на зажимах цепи и тока, проходящего через данную цепь, связаны соотношением,
аналогичным закону Ома:
22
где ,; xrzziUzIU
mm
+=== называется полным
сопротивлением рассматриваемой цепи.
Если задано напряжение )sin(
ψ
ω
+
=
tUu
m
на зажимах цепи с последовательно
соединенными r,L,C, то ток определяется по формуле
).sin(
ϕψω
−+= t
z
U
i
m
Угол φ, равный
разности начальных фаз напряжения и тока, отсчитывается по оси ωt в направлении от
напряжения к току и бывает острым или прямым
.2
πϕ
≤
Угол
φ положителен при индуктивном характере цепи, то есть при x>0; при этом ток
отстает по фазе от напряжения и
φ отсчитывается по оси абсцисс вправо от напряжения к
току (рис.3.11а).
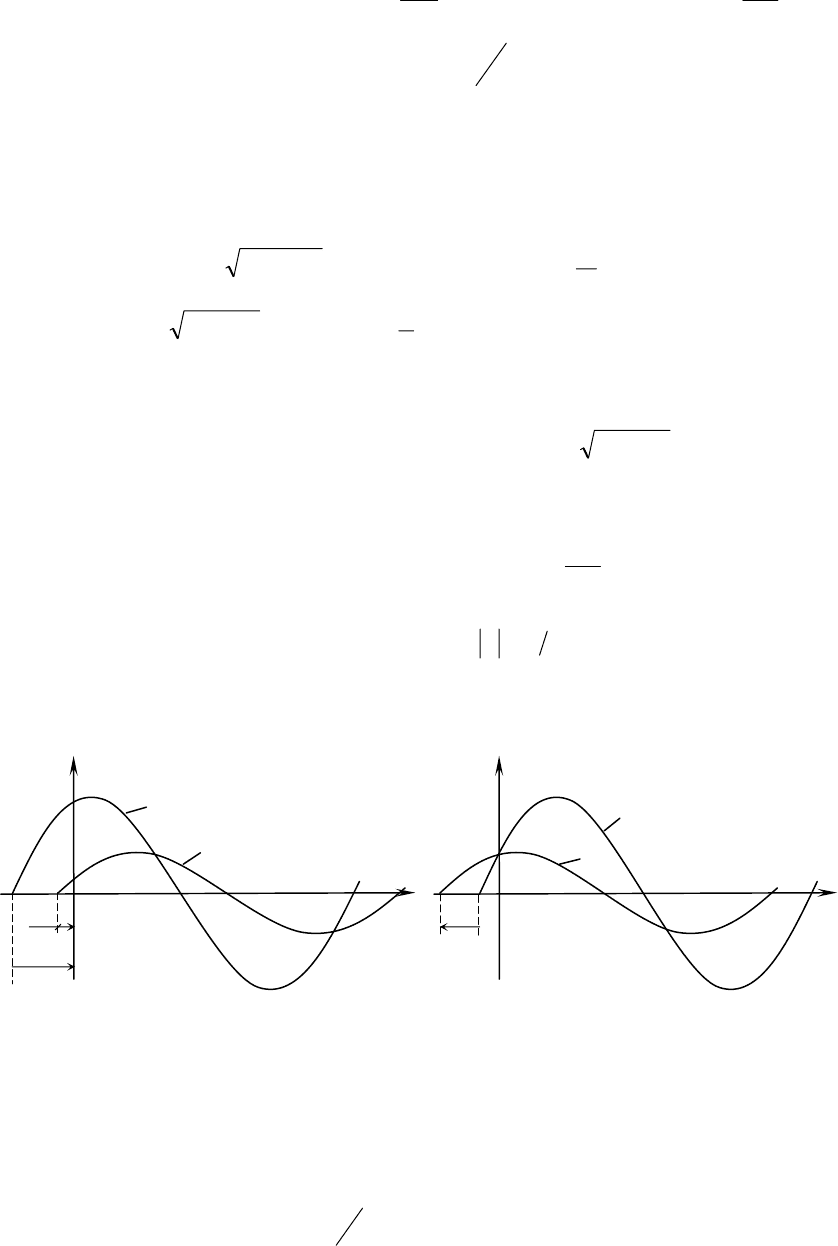
Рис.3.11а Рис.3.11б
Угол
φ отрицателен при емкостном характере цепи, то есть при x<0; при этом ток
опережает по фазе напряжение и
φ отсчитывается по оси абсцисс влево от напряжения к току
(рис.3.11б).
Ток совпадает с напряжением по фазе при 0
=
−
=
CL
xxx . Такой режим работы
электрической цепи называется резонансом напряжений.
В этом случае индуктивное сопротивление
ωL становится равным емкостному
сопротивлению
1/ωC , то есть
C
L
ω
ω
1
= .
0
t
ω
i
ψ
0>
ϕ
u
ψ
u
i
iu,
u
0
<
ϕ
t
ω
i
iu
,
0
