Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

видно,

что

даже

если у среднего нет тренда,- то он имеется у

дисперсии.

Теперь предположим, что истинной моделью является

DSP,

т!е. уравнение

(12.2)

с ß=0, а оценивается ошибочно

модель типа TSP (12.1):

т.е. модель с линейным трендом среднего, но без тренда у

дисперсии. Априори

ясно,

что возрастающая дисперсия слу-

чайной

компоненты означает широкие движения и,, кото-

рые

будут

приписаны дрижению среднего, и коэффициент ß

при

переменной времени t окажется значимым,

даже

если в

действительности никакого тренда у среднего нет. Каковы

будут

последствия ошибочной спецификации? К. Нельсон и

Г. Канг [155] анализировали эту проблему и сделали

следу-.

ющие выводы:

1. Регрессия случайного блуждания на время, оценен-

ная

МНК,

дает

в районе 0,44 независимо от объема вы-

борки,

когда в действительности среднее значение перемен*

ной

не связано с временем каким-либо образом.

2. В

случае

когда случайное блуждание имеет дрейф,

т.е. ß * 0, R

будет

выше и

будет

увеличиваться с ростом

объема выборки, достигая в пределе 1, независимо от зна-

чения

ß.

Остатки от регрессии на время, рассматриваемые как

ряд с исключенным трендом, имеют в среднем только около

14% истинной дисперсии стохастической компоненты исход-

ного ряда. .

4. Остатки от регрессии на время автокоррелированы и

коэффициент

автокорреляции для лага 1 г,«

1—10/п,

где

—

объем выборки.

5. Обычные /-критерии для проверки значимости отдель-

ных регрессоров более не работают. Имеется тенденция от-

вергать на их основе

нулевую

гипотезу о независимости от

времени, когда она верна.

6. Регрессия одного случайного блуждания на

другое

включением времени в правую часть уравнения с высокой

вероятностью приводит к ложным зависимостям, т.е. обыч-

ная

/-статистика часто указывает на связь

между

перемен-

ными,

когда ее нет.

271

Основной

вывод состоит в том, что использование рег-

рессии на время имеет серьезные последствия, когда в дей-

ствительности временной ряд относится к классу DSP и,

следовательно, адекватной процедурой для исключения трен-

да является переход к разностям.

Теперь предположим, что истинной является модель ли-

нейного тренда, а мы перешли к разностям. Тогда ошибка

имеет характер скользящей средней, и в

худшем

случае

иг-

норирование этого приведет к неэффективным оценкам.

Например,

пусть истинная модель

гдем, — независимы, с нулевым средним и постоянной диспер-

сией.

Если перейти к первым разностям, то получим

где ошибка V,

Дм,

—

«,_, является скользящей средней

и,

следовательно, автокоррелированной. В этом

случае

оце-

нивание

МНК уравнения для первых разностей все еще

дает

состоятельные оценки. Таким образом, последствия перехо-

да к разностям, когда этого не требуется, намного менее

серьезны, чем те, что связаны с непереходом к разностям,

когда это обусловлено свойствами ряда, т.е. когда истинная

модель относится к классу DSP.

Нельсон

и Плоссер применили критерий Дикки — Фул-

лера для проверки широкого круга исторических времен-

ных рядов, описывающих экономику США, и пришли к вы-

воду,

что во

всех

случаях

следует

принять гипотезу DSP, за

исключением нормы безработицы. Они

делают

вывод, что

для большинства экономических временных рядов модель

DSP

более адекватна, а модель TSP была бы подходящей

только, если предположить, что ошибки u

(12.1)

сильно

автокоррелированы.

Таким

образом, для

учета

тренда на практике

лучше

использовать переход к разностям и строить регрессии на

их основе, чем регрессии для уровней с временем в качестве

Дополнительной объясняющей переменной.

А теперь рассмотрим подробнее процедуру Дикки -

Фуллера.

272

§ 3. КРИТЕРИЙ

ДИККИ

- ФУЛЛЕРА

ДЛЯ

ОБНАРУЖЕНИЯ ЕДИНИЧНЫХ КОРНЕЙ

Задача проверки гипотезы р = 1 в авторегресси-

онном

уравнении первого порядка '

(12.5)

называется

проверкой

наличия

единичных

корней.

Процесс

у,

является стационарным, если —1 < р < 1. Если р = 1, то

нестационарный и модель

(12.5)

представляет случай-

ное

блуждание с дрейфом. Если р > 1, ряд имеет нестацио-

нарный,

взрывной характер. Поэтому гипотеза о стационар-

ности

ряда может быть проверена путем сравнения pel.

Однако обычный критерий МНК. - ^-статистика здесь не-

применим

требует

корректировки. Рассмотрим этот воп-

рос подробнее.

Найдем дисперсию оценки МНК

р"

для больших выборок

модели парной регрессии (12.5), воспользовавшись фор-

мулой

(12.6)

где в качестве объясняющей переменной x

выступает лаго-

вое значение y

{

. Последовательно раскрывая y

через про-

шлые (лаговые) значения у, получаем

Математическое ожидание:

Дисперсия:

273

lg-1866

Отсюда, после подстановки в (12.6), получаем

где

— объем выборки.

Таким

образом, уагф)

0при нулевой гипотезе Н

: р= I.

Следовательно; для того чтобы можно было применять этот

критерий,

нужно получить предельное распределение р при

нулевой гипотезе Н

: р= 1.

Одним

из наиболее широко используемых критериев

наличия

единичных корней является критерий Дикки -

Фуллера. Они начали с построения процедуры проверки

гипотезы Н

: р = 1 в модели (12.5):

Этот тест выполняется путем оценивания уравнения,

получаемого после перехода к разностям, когда модель за-

писывается

как

где у=р- 1.

Проверка

гипотезы р - 1 эквивалентна проверке гипоте-

зы

у=» 0. Затем авторы рассмотрели три различных регрес-

сионных

уравнения, в которых проверяется наличие еди-

ничного

корня:

(12.7)

(12.8)

(12.9)

Отметим, что рассмотренная ранее модель

(12.4)

может

быть приведена к виду

(12.9)

при у= р - 1.

Различие

в моделях (12.7),

(12.8)

(12.9)

состоит в нали-

чии

детерминированных элементов а и ß/. Первая модель -

это

модель чисто случайного блуждания, во вторую модель

274

добавляется свободный член, который является парамет-

ром дрейфа, а в третью — включены и дрейф, и линейный

временной

тренд.

Во всех

трех

регрессиях интерес представляет параметр у,

если у=0, то ряд у, характеризуется единичным корнем р=1.

Процедура проверки предполагает оценивание МНК одно-

го иди нескольких записанных выше уравнений с целью

получения оценки у и ее стандартной ошибки. Делением

оценки

на ее стандартную ошибку получают /-статистику,

которая,

однако, при нулевой гипотезе о наличии единично-

го корня имеет распределение, отличное от распределения

Стьюдент^. Авторы получили критические значения для /

путем модельных статистических испытаний. Сравнение

полученных /-статистик с критическим значением, приве-

денным в таблицах Дикки — Фуллера, позволяет исследо-

вателю принять или отвергнуть

нулевую

гипотезу Н

: у

Пусть, например, оценивание модели

дало следующие результаты: р

=»

0,9546

с о =

0,030.

Тогда

оценка

МНК уравнения в разностном виде

дает

у==

-0,0454

с той же самой стандартной ошибкой

0,030.

Следовательно, соответствующая /-статистика для гипотезы

Y=0 равна:

/ -

-0,0454

0,030

- -1,5133.

Для каждого из

трех

видов регрессионных уравнений

(12.7),

(12.8)

(12.9)

методология остается одинаковой. Од-

нако

нужно иметь в

виду,

что критические значения /-ста-

тистик

зависят от вида уравнения, от включения свободно-

го члена или временного тренда. В своем исследовании

методом Монте-Карло Дикки и Фуллер нашли критические

значения

для гипотезы у— 0 в зависимости от вида регрес-

сии

и объема выборки. Эти статистики для

трех

видов рег-

рессии обозначены как х, г и т

соответственно. В табл. 12.1

275

18*

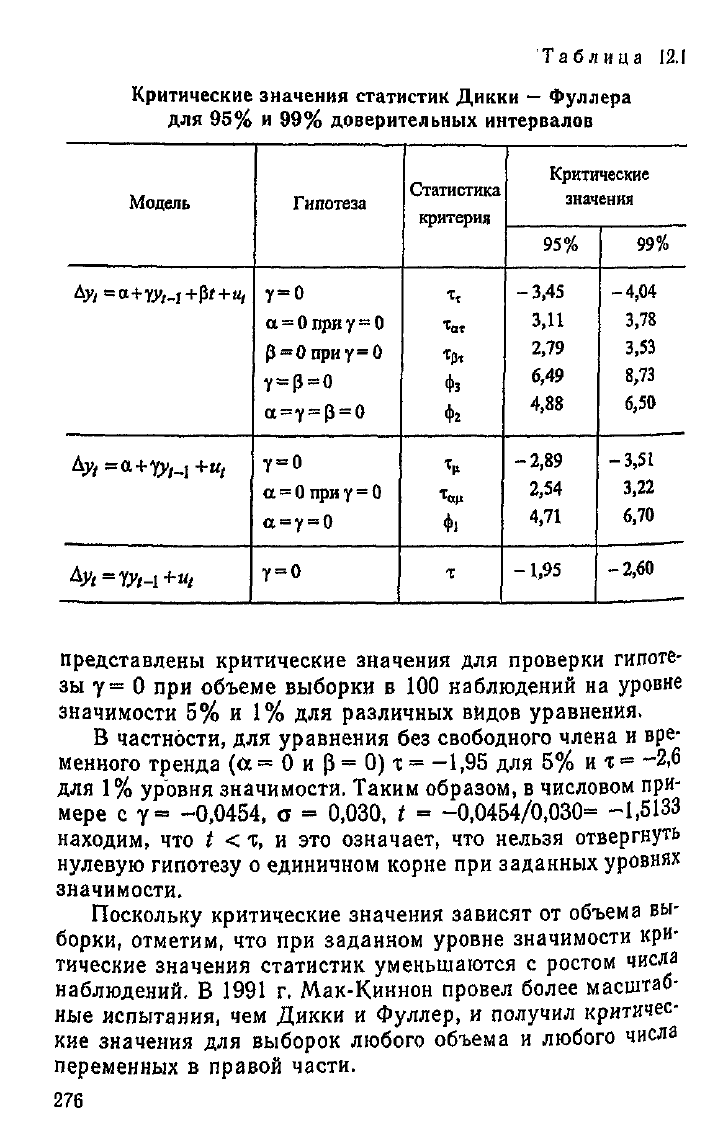
Таблица 12.1

Критические значения статистик Дикки —

Фуллера

для 95% и 99%

доверительных

интервалов

Модель

Ay,

а+у

+и,

&У1=УУ

(

-1+Щ

Гипотеза

y=0

при

—

при

у=0

ß = O

a=y=ß=0

0 при у

сс

у = 0

Статистика

критерия

*т

Т«

Фз

*М

Ф»

Критические

значения

95%

-3,45

3,11

2,79

6,49

4,88

-2,89

2,54

4,71

-1,95

99%

-4,04

3,78

3,53

8,73

6,50

-3,51

3,22

6,70

-2,60

представлены критические значения для проверки гипоте-

зы у= 0 при объеме выборки в 100 наблюдений на уровне

значимости 5% и 1% для различных видов уравнения.

В частности, для уравнения без свободного члена и вре-

менного тренда (ос= 0 и ß= 0) т= -1,95 для 5% и t= -2,6

для 1% уровня значимости. Таким образом, в числовом при-

мере су-

-0,0454,

a =

0,030,

t =

-0,0454/0,030=

-1,5133

находим, что t <

и это означает, что нельзя отвергнуть

нулевую

гипотезу о единичном корне при заданных уровнях

значимости.

Поскольку критические значения зависят от объема вы-

борки,

отметим, что при заданном уровне значимости кри-

тические значения статистик уменьшаются с ростом числа

наблюдений. В 1991 г. Мак-Киннон провел более масштаб-

ные испытания, чем Дикки и Фуллер, и получил критичес-

кие

значения для выборок любого объема и любого числа

переменных в правой части.

276

§ 4. РАСШИРЕННЫЙ КРИТЕРИЙ

ДИККИ

- ФУЛЛЕРА

По-английски

этот критерий называется

Augmented

Dickey-Fuller

Test (ADF). Если обычный критерий Дикки -

Фуллера позволяет проверять гипотезу о наличии авторег-

рессии первого порядка, то расширенный предназначен для

идентификации

авторегрессии более высоких порядков.

Итак,

не все временные ряды

могут

быть хорошо пред-

ставлены авторегрессионным процессом первого порядка.

Рассмотрим авторегрессионный процесс р-го порядка

(12.10)

Прибавим

и вычтем

p+l

получим

Вновь прибавим и вычтем получим

Продолжая этот процесс и вычитая г/

из левой и пра-

вой части, приходим к следующему выражению:

(12.11)

(12.12)

(12.13)

277

Интерес

представляет коэффициент у. Если он равен

нулю, уравнение

(12.11)

оказывается полностью записан-

ным

через первые разности, и таким образом имеется еди-

ничный

корень. Проверка наличия единичного корня может

быть осуществлена с помощью тех же самых статистик кри-

терия Дикки

—

Фуллера, распределения которых зависят от

включения в регрессионное уравнение детерминированных

компонент.

Другими словами, расширенный критерий Дикки

—

Фул-

лера используется для проверки наличия единичного корня

авторегрессионных уравнениях более высокого порядка,

имеющих следующий вид:

(12.14)

(12.15)

(12.16)

Если нет свободного члена и тренда, используется ста-

тистика х; если включен только свободный член, использу-

ется статистика х, а если

присутствует

и свободный член, и

тренд, то — статистика x

• Отметим, что из

(12.12)

следует,

что если сумма

коэффи-

циентов исходного уравнения равна 1, т.е. 2^а,

=1.

то Y^ ^

а это значит, что имеется единичный корень. Для проверки

совместных гипотез о значениях коэффициентов Дикки и

Фуллер [138] предложили еще три статистики, названные

ими

ф,, ф

и ф

. Для уравнений

(12.8)

или

(12.15)

нулевая

гипотеза Н

у=сс=

0 проверяется по статистике ф,. Если

регрессию включается временной тренд и оцениваются

уравнения

(12,9)

или (12.16), то совместная нулевая гипоте-

за Н

ß = Y

0 проверяется по статистике ф

, а гипотеза

ß = 0 - по статистике ф

278

Статистики

ф,,

и ф

приведены нами в той же таблице.

Они

построены точно так же, как и обычные /^-статистики

для сравнения общей модели с частной [128]:

(12.17)

где

- коэффициент детерминации общей модели (без

ограничений UnRestricted);

коэффициент

детерминации частной модели (с ог-

раничениями

- Restricted);

т — число ограничений (число параметров, прирав-

ниваемых нулю);

п — объем исходной выборки;

р - порядок лага;

— число параметров, оцениваемых в общей модели,

(п-

р -

А)

—

число степеней свободы модели без ограничений.

Формулу

(12.17)

можно эквивалентным образом запи-

сать через суммы квадратов ошибок

CKO

ü/?

СКО

для

соответствующих моделей. Так как

(12.18)

Отметим, что критические значения статистик

Дикки

Фуллера намного выше, чем в обычных таблицах

F-pac-

пределения. Для сравнения приведем их для

5%-ного

уров-

ня

значимости (табл. 12.2), числе степеней свободы числи-

теля 2 и числе степеней свободы знаменателя (п - р - 3).

В качестве иллюстрации рассмотрим пример, описан-

ный

Дикки и Фуллером. Они предположили, что логариф-

мы квартальных данных об индексе производства, рас-

считываемым Федеральной резервной палатой, можно адек-

ватно представить за период с I кв. 1950 г. по IV кв. 1977 г.

моделью:

279

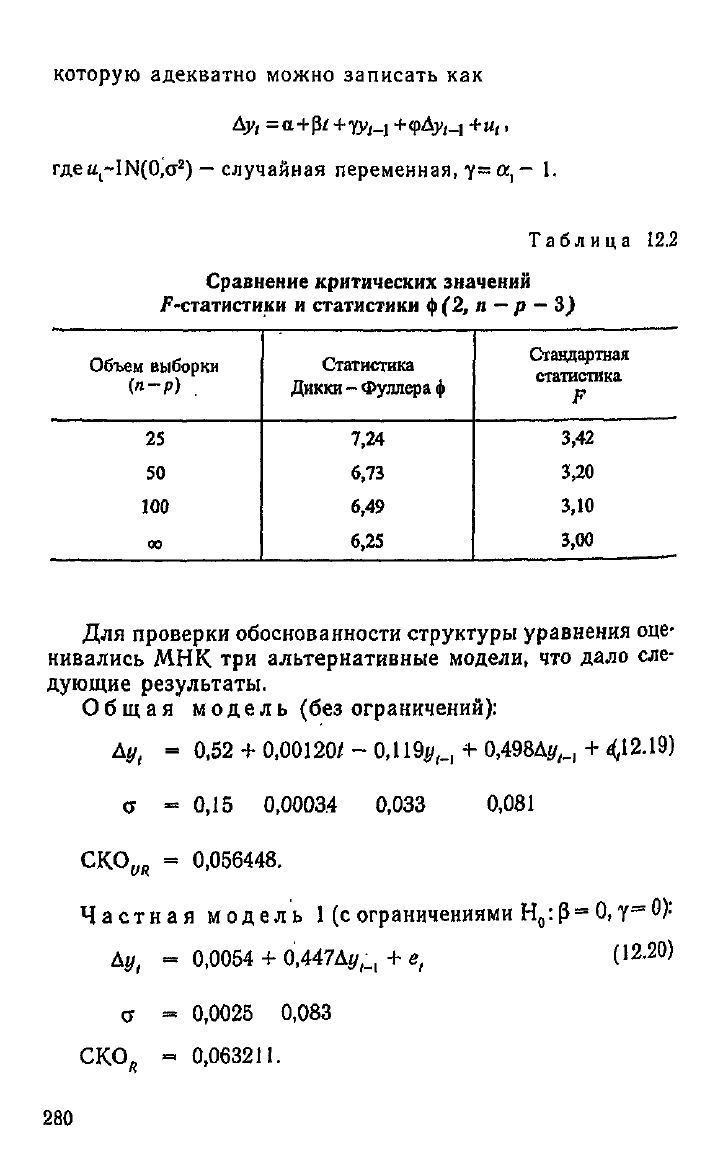
которую адекватно можно записать как

где

u,~IN(0,a

)

—

случайная переменная, у= а,

—

Таблица 12.2

Сравнение критических значений

^-статистики и статистики

(2, п - р - 3)

Объем выборки

(п-р)

100

Статистика

Дикки - Фуллера

7,24

6,73

6,49

6,25

Стандартная

статистика

3,42

3,20

3,10

3,00

Для проверки обоснованности структуры уравнения оце-

нивались МНК три альтернативные модели, что дало сле-

дующие результаты.

Общая модель (без ограничений):

äy

- 0,52 +

0,00120/

0,119у

0,498Дг/,_,

+ <12.19)

a =0,15

0,00034

0,033

0,081

СКО^

0,056448.

Частная модель 1 (с ограничениями

:ß=

0, у^^

At/, =

0,0054

0,447At/,_,

+ е, (J

20)

a -

0,0025

0,083

CKCL

- 0,063211.

280