Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

Весьма важный вопрос, оставленный Р.Г. Брауном без

ответа, касается выбора оптимального значения параметра

адаптации а. Формула

(11.10)

лишь

свидетельствует

о том,

что чем ближе

ос

к нулю, тем меньше дисперсия оценки веро-

ятности.

Но нас в конечном счете интересует не столько ее

колеблемость, сколько степень соответствия последователь-

но

формируемого и корректируемого распределения (точнее,

гистограммы) характеру реального разброса значений ис-

следуемой величины, по предположению, изменяющемуся во

времени. Совершенно очевидно, что вопрос об оптимальном

значении

параметра а может быть решен только при нали-

чии

критерия качества рассматриваемой процедуры.

За

основу такого критерия в [123] предлагается взять

максимальный уровень значимости, при котором получен-

ную в момент t фактическую точку можно отнести к постро-

енному на этот же момент распределению. Сумма (или нор-

мированная

сумма) таких максимальных уровней значимости

по

моментам времени t = 1,2, ..., Т

даст

значение итогового

критерия

Q, который

будет

функцией параметра адапта-

ции

начальных оценок вероятностей событий на момент

0. Максимальная величина Q определяет оптимальное

значение а и начальных оценок вероятностей.

Поясним

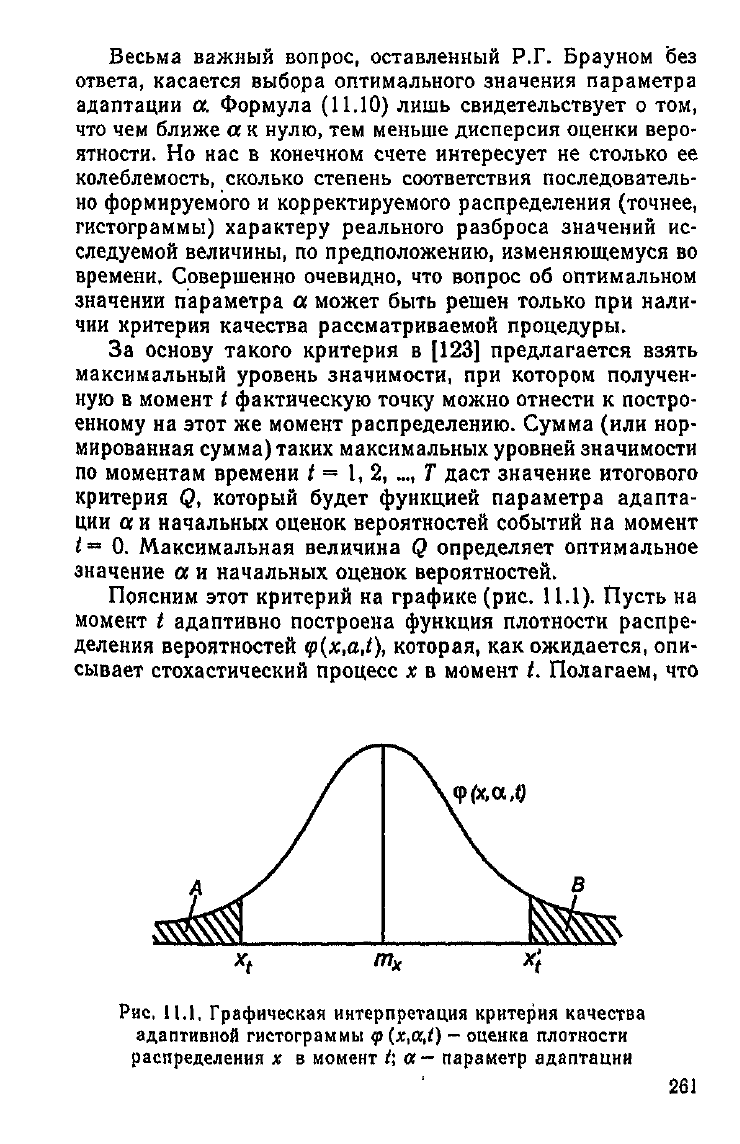
этот критерий на графике (рис. 11.1). Пусть на

момент t адаптивно построена функция плотности распре-

деления вероятностей (p(x,a,t), которая, как ожидается, опи-

сывает стохастический процесс х в момент /. Полагаем, что

Рис,

11.1. Графическая интерпретация критерия качества

адаптивной гистограммы

<р

(x,a,t) — оценка плотности

распределения х в момент t\ а— параметр адаптации

261

момент

t мы

получаем значение

(

(реализацию) исследу-

емой величины

х.

Тогда заштрихованная область

под кри-

вой распределения равна вероятности того,

что х

примет

значение меньше

, и

представляет собой максимальный

уровень значимости

maxt

, при

котором

еще

можно

счи-

тать принадлежащей генеральной совокупности

плотнос-

тью распределения (p(x,a,t).

Если

бы

наблюденное значение превосходило медиану

равнялось

х\, то

максимальный уровень значимости

определялся

бы

заштрихованной областью

В.

Изложенное

можно записать

так:

(11.15)

где

Рг

— вероятность;

медиана распределения х\

Ф(х,а^)'~ интегральная функция распределения

х,

(11.16)"

Сама динамика

mMi

может показать,

какие периоды

соответствие гистограмм и реальных наблюдений было

«луч-

ше»,

а в

какие —

«хуже».

Суммирование

по

всем временным точкам выборки

по-

зволяет сформировать критерий качества

для

процеду-

ры

целом:

(11.17)

или

его

нормированный вариант

(11.18)

262

Критерий

Q, является агрегатом, характеризующим сте-

пень

соответствия наблюдений временного ряда и ряда по-

строенных гистограмм на всем выборочном интервале в це-

лом. Критерий Q

интерпретируется как усредненное по

выборке максимальное значение уровня значимости, при

котором наблюденные значения ряда можно считать при-

надлежащими распределениям, представляемым соответ-

ствующими гистограммами.

В формулах

(11.17)

(11.18)

показано, что в обоих

случа-

ях критерий .качества процедуры адаптации является функ-

цией

не только данных {х,} и параметра адаптации а, но и

объема выборочных данных Т

используемых для определе-

ния

начальных значений вероятностей событий, необходи-

мых для запуска рекуррентной процедуры.

Отметим также, что Q, и Q

сформированы как односто-

ронние

критерии, предполагающие, что сопоставление реа-

лизации

процесса х

(

с построенным распределением произ-

водится на одном его

«хвосте».

Однако на самом

деле

фактические точки случайным образом ложатся по обе сто-

роны

от медианы, и поэтому целесообразно перейти к дву-

стороннему критерию, для которого все значения q нужно

лишь удвоить. Тогда получим критерий <?

(11.19)

Критерий

можно интерпретировать как достигнутый

среднем по выборке уровень значимости, при котором

выборочные значения исходного ряда x

принадлежат рас-

пределениям вероятностей, построенным для соответствующих

моментов времени. Ясно, что чем выше значение критерия,

тем

лучше

процедура адаптации

«успевает»

за изменениями

реальном процессе.

Очевидно, что Q

принимают максимальное зна-

чение одновременно, т.е. при одних и тех же а

Т,. Замеча-

тельное свойство критерия

(11.19)

состоит в том, что если,

начиная

с какого-то момента времени, переменная х, при-

нимает постоянное значение, равное медиане, то все после-

дующие

mMl

равны 0,5,

-±l,

a распределение постепенно

стягивается в точку. В общем

случае

значение критерия

263

находится в пределах 0 <

< 1, и это

делает

его удобным

для различных сопоставлений.

Следует

отметить, что при использовании построенной

гистограммы для выработки вероятностных суждений мо-

гут применяться как односторонний, так

двусторонний кри-

терии в зависимости от задач, и результаты, конечно,

будут

различные.

Имея

критерий качества процедуры, нетрудно определить

оптимальное значение параметра адаптации а. Для этого

надо на интервале 0 < сс< 1, например, методом проб найти

такое его значение, которое максимизирует Q. Точно так же

можно найти и оптимальное значение Т, — начальную часть

выборки,

используемую для вычисления

грубых

оценок ве-

роятностей

(0),

необходимых для первого применения ре-

куррентных формул экспоненциального сглаживания.

Конечно,

оптимизация критерия Q по

двум

параметрам

а и Г, несколько усложняет вычислительный процесс. Но,

во-первых, область определения обоих параметров ограни-

чена: 0 < ос< 1, 1

«Т

<,Т.

Во-вторых, применение сначала

грубой сетки значений для локализации области поиска, а

затем более тонкой помогают резко снизить объем вычисле-

ний.

В-третьих,

быстродействие современных компьютеров

делает

проблему легко преодолимой.

§ 4. АДАПТИВНЫЙ АНАЛИЗ РАСПРЕДЕЛЕНИЯ

КАССОВЫХ ОСТАТКОВ

Необходимость анализа нестационарных распре-

делений часто возникает в экономических исследованиях.

Например,

в банковской деятельности это может быть за-

дача

изучения распределения сумм на корреспондентских

счетах

или в более общей постановке — анализ и использо-

вание вероятностных закономерностей формирования кас-

совых остатков.

В качестве примера рассмотрим

задачу

о кассовых ос-

татках. Предположим, что имеются ежедневные данные об

остатках наличных средств, являющихся результатом дви-

жения

денег за день. Необходимо определить, какую

сумму

из

этого остатка можно пустить в оборот, обеспечив при этом

заданную вероятность незамедлительного удовлетворения

запросов клиентов с

учетом

ожидаемых новых поступлений.

264

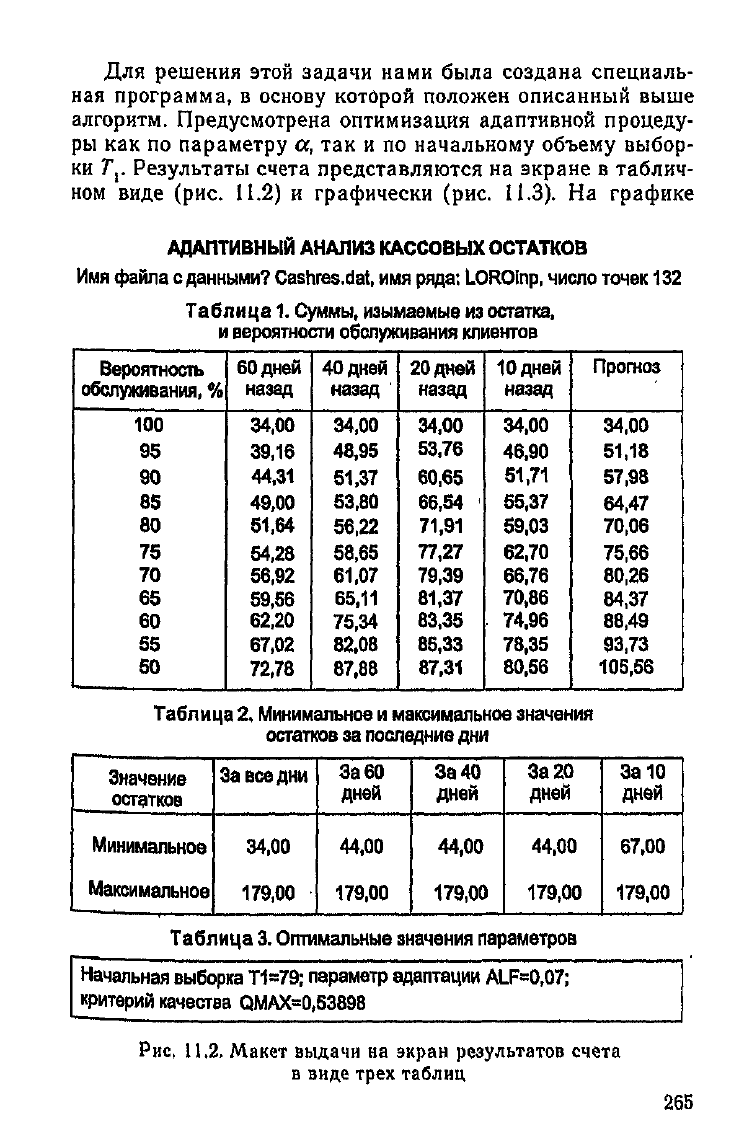
Для решения этой

задачи

нами

была

создана

специаль-

ная

программа,

основу

которой положен описанный

выше

алгоритм.

Предусмотрена

оптимизация адаптивной

процеду-

ры как по

параметру

а, так и по

начальному

объему

выбор-

ки T

Результаты

счета

представляются

на экране в

таблич-

ном

виде

(рис. 11.2) и графически (рис.

11.3).

На графике

АДАПТИВНЫЙ АНАЛИЗ КАССОВЫХ ОСТАТКОВ

Имя файла сданными? Cashres.dat, имя ряда: LOROinp, число точек 132

Таблица

Суммы, изымаемые из остатка,

и вероятности обслуживания клиентов

Вероятность

обслуживания, %

100

60 дней

34,00

39,16

44,31

49,00

51,64

54,28

56,92

59,56

62,20

67,02

72,78

40 дней

34,00

48,95

51,37

53,80

56,22

58,65

61,07

65,11

75,34

82,08

87,88

20 дней

34,00

53,76

60,65

66,54

71,91

77,27

79,39

81,37

83,35

85,33

87,31

10 дней

34,00

46,90

51,71

55,37

59,03

62,70

66,76

70,86

74,96

78,35

80,56

Прогноз

34,00

51,18

57,98

64,47

70,06

75,66

80,26

84,37

88,49

93,73

105,56

Таблица

Минимальное и максимальное значения

остатков

за последние дни

Значение

остатков

Минимальное

Максимальное

За

все дни

34,00

179,00

За

дней

44,00

179,00

За

дней

44,00

179,00

За

дней

44,00

179,00

За

дней

67,00

179,00

Таблица

Оптимальные значения параметров

Начальная

выборка Т1=79; параметр адаптации ALF=0,07;

критерий

качества QMAX=0,53898

Рис,

11,2,

Макет

выдачи на

экран

результатов счета

виде трех таблиц

265

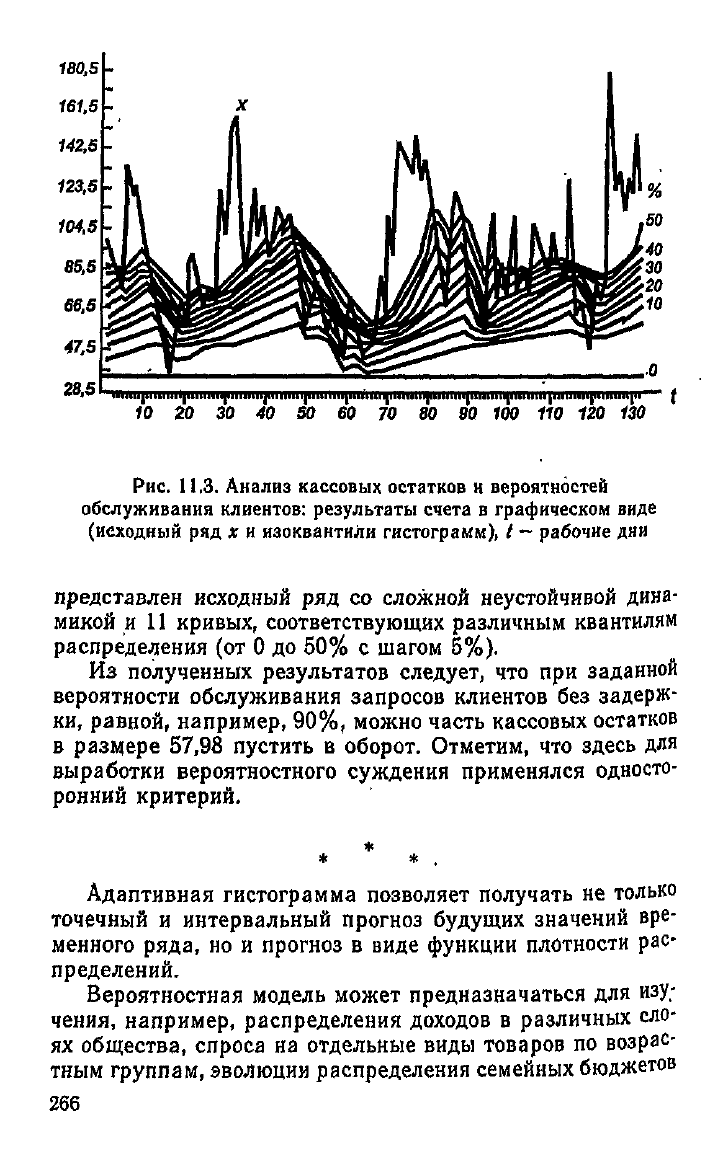
Рис.

11.3. Анализ кассовых остатков и вероятностей

обслуживания клиентов:

результаты

счета

в графическом виде

(исходный ряд х и изоквантили гистограмм), t

—

рабочие дни

представлен исходный ряд со сложной неустойчивой дина-

микой

и 11 кривых, соответствующих различным квантилям

распределения (от 0 до 50% с шагом 5%).

Из

полученных результатов

следует,

что при заданной

вероятности обслуживания запросов клиентов без задерж-

ки,

равной, например, 90%, можно часть кассовых остатков

размере

57,98

пустить в оборот. Отметим, что здесь для

выработки вероятностного суждения применялся односто-

ронний

критерий.

Адаптивная гистограмма позволяет получать не только

точечный и интервальный прогноз

будущих

значений вре-

менного ряда, но и прогноз в виде функции плотности рас-

пределений.

Вероятностная модель может предназначаться для изу-

чения,

например, распределения

доходов

в различных сло-

ях общества, спроса на отдельные виды товаров по возрас-

тным группам, эволюции распределения семейных бюджетов

266

по

статьям расходов, распределения сумм текущих вкладов

других

финансовых, экономических и социально-экономи-

ческих процессов.

Особое значение предложенный

подход

имеет для ана-

лиза рисков, и, в частности, в анализе, получившем назва-

ние

Value

Risk

(VAR).

Такой анализ позволяет оценить

величину максимального обесценения актива при заданном

уровне значимости (вероятности).

Предложенная процедура адаптивного исследования

распределений применима при определении размеров раз-

личных резервных и

страховых

фондов. С ее помощью мож-

но,

например, анализировать изменения в распределении

депозитов по величине и сроку, непрерывно обновлять таб-

лицы

смертности, рождаемости, заболеваемости, используе-

мые в страховой медицине, а также таблицы аварий и пожа-

ров,

используемые в страховании автомобилей, недвижимости

т.д.

Подобные задачи возможны и в

«технологических»

зве-

ньях в связи с исследованием надежности и качества с уче-

том непрерывной модернизации технологий и модификации

изделий и т.п.

Имеются резервы и для совершенствования рассмотрен-

ной

методики. Так, в данном изложении мы полагали, что

параметр адаптации постоянен. Между тем скорость де-

формации

распределения со временем может существенно

меняться.

Тогда возникает задача автоматического управ-

ления

параметром адаптации (см. гл. 4). Заметное влияние

на

эффективность процедуры

могут

оказывать также силь-

ные тренды временного ряда. В этом

случае

процедура об-

новления

гистограммы отстает от реальных изменений, что

проявляется в снижении показателя качества Q. Такие воп-

росы

требуют

специального изучения в каждом отдельном

случае.

Глава

КРИТЕРИИ

ДИККИ-ФУЛЛЕРА

ДЛЯ

ИДЕНТИФИКАЦИИ

ХАРАКТЕРА

ТРЕНДА

(ОБНАРУЖЕНИЕ

ЕДИНИЧНЫХ

КОРНЕЙ)

Экономические ряды очень часто характеризуют-

ся

наличием временного тренда. Обнаружение трендов и их

правильный

учет

в структуре модели представляют собой

важную задачу в анализе временных рядов. Для решения

этой

задачи Дикки и Фуллер разработали критерии [137,138],

рассмотрению которых и посвящена данная глава.

§ 1. ДЕТЕРМИНИРОВАННЫЙ

СЛУЧАЙНЫЙ

ХАРАКТЕР

ТРЕНДА

В экономических исследованиях часто приходится

иметь дело с нестационарными временными рядами, обнару-

живающими тот или иной тренд. При построении регрессион-

ной

модели необходимо учитывать наличие этого тренда и ис-

ключать его. Известны две процедуры исключения тренда:

1) оценивание регрессии на время;

2) переход к последовательным разностям (приростам)

переменной.

В регрессионном подходе предполагается, что ряд у, ге-

нерируется моделью

где f(t) - тренд;

и, - стационарная случайная компонента с нулевым ма-

тематическим ожиданием и дисперсией

<з\.

268

Если предположить, что f(t) является линейной функ-

цией

от времени, то

(12.1)

После элиминирования тренда остается ряд ошибок ме-

тода наименьших квадратов (МНК) e

со свойствами £е,=

Ste,= 0.

Если для элиминирования тренда перейти к разностям,

то получим

Для элиминирования ß нужно еще раз взять разности

первого порядка

Полученный ряд не содержит тренда. Однако, если пред-

положить, что у

(

генерирован моделью

(12.2)

где е, - стационарный ряд с нулевым математическим ожида-

нием

и дисперсией о

; в этом случае первые разности

оказываются стационарными с математическим ожи-

данием ß. Эта модель называется

моделью

случайного

блуждания

дрейфом.

Переходя от начального значения у

к y

путем суммиро-

вания

приращений, получим выражение

(12.3)

имеющее тот же общий вид, что и уравнение (12.1), за исклю-

чением того, что член возмущения не является стационарным,

так

как его дисперсия to

растет во времени. К« Нельсон и

К.

Плоссер [153] назвали выражение

(12.1)

моделью

детер-

минированным

трендом

(trend-stationary

processes

- TSP), a

уравнение

(12.2)

—

моделью

стационарных

приращений

(difference-stationary

processes

— DSP). Обе модели отража-

ют линейный тренд, но различаются способом элиминирова-

ния

тренда из исходных данных.

269

Для проверки гипотезы о том,.что ряд генерирован моде-

лью TSP против альтернативной, которая означает, что ряд

описывается моделью DSP, К. Нельсон и К. Плоссер предло-

жили применять критерий, разработанный Д. Дикки

В. Фул-

лером [137, 138]. Критерий предполагает оценку модели:

(12.4)

Ряд

принадлежит к классу DSP, если р = 1, ß= 0, и к

классу TSP — если р=0 или в более широком смысле, если

1р|<Г.

Таким

образом, нужно проверить

нулевую

гипотезу Н

р=

1, ß= 0 против альтернативной Н,: |р| < 1.Проблема,

возникающая

здесь, состоит в том, что нельзя использовать

обычную теорию распределения оценок МНК, когда р= 1.

Дикки

и Фуллер показали, что оценка МНК параметра р

при

гипотезе о модели DSP (т.е., что р= 1) имеет математичес-

кое ожидание не 1, а значение, меньшее 1. Однако отрица-

тельное смещение уменьшается с увеличением числа наблю-

дений.

Авторы

критерия получили критические значения для

проверки гипотезы р= 1 против |р| < 1.

Процедура проверки гипотез относительно характера

тренда является частным случаем более общей процедуры

идентификации

авторегрессионной зависимости, которую мы

рассмотрим

чуть

позже, а сейчас обсудим последствия не-

верной спецификации модели.

§2.

ЛОЖНЫЕ ТРЕНДЫ

Если в уравнении (12.2), представляющем модель

DSP,

ß=0

то получаем модель случайного блуждания без тренда (ее

также называют

случайным

блужданием

нулевым

дрей-

фом). Однако из представления этой модели в виде выра-

жения

(12.3)

270