Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

Альтернативный вариант критерия

для

регрессионных

моделей выражается через

(12.33)

В соответствии

этим вариантом критерия выбирается

модель

наименьшим значением SBC

Оба

варианта крите-

рия

приводят

одинаковому выбору модели. Однако резуль-

таты критериев Акайка

Шварца

могут

немного отличаться.

Как

правило,

при

выборе порядка лага

авторегрессионной

модели критерий Акайка указывает

на

больший порядок,

что означает большую величину

«штрафа»

за

добавление

переменной

правую часть уравнения

критерия Шварца.

Общий критерий множителей Лагранжа

для обнаружения автокорреляции остатков

Обычно

для

обнаружения автокорреляции

регрессион-

ных остатках применяется критерий Дарбина

—

Уотсона,

ко-

торый обозначается

как DW

или

как d.

Однако

он

неприме-

ним

случае, когда среди регрессоров имеются лаговые

значения

эндогенной переменной.

На

это указали сами авто-

ры критерия, и одним из них, Дарбиным, был предложен

аль-

тернативный h-критерий, который, однако, можно вычислить

не

всегда.

И,

кроме того,

оба

критерия

и h

являются

критериями

автокорреляции только первого порядка. Breusch

(1978),

Godfrey

(1978)

рассматривают несколько общих тес-

тов, которые легко применять

сохраняют свою силу при очень

общих гипотезах относительно автокорреляции

регрессион-

ных остатках. Эти критерии получены

на

основе общего прин-

ципа,

называющегося принципом множителей Лагранжа. Один

из

них, критерий множителей Лагранжа (LM-test), является

более общим

позволяет обнаруживать

регрессионных ос-

татках автокорреляцию

более высоких порядков.

Как и h-

тест,

он применим только для больших выборок.

Рассмотрим регрессионную модель

(12.34)

которой

291

(12.35)

Необходимо проверить нулевую гипотезу Н

Среди объясняющих переменных

могут

быть лаговые

значения

зависимой переменной. LM-тест состоит из

следу-

ющих шагов:

1)оценить регрессию

(12.34)

методом наименьших квад-

ратов, получить остатки ü

;

2) оценить регрессию

(12.36)

проверить, не являются ли все коэффициенты р, при лаго-

вых значениях остатков нулевыми. Для этого вычисляется

F-статистика и рассматривается pF как

(р).

Здесь исполь-

зуется х

-критерий, а не F, так как LM-тест предназначен

для больших выборок.

Этот критерий может быть использован для различных

спецификаций

процесса, описывающего ошибки регрессии.

Например,

при проверке автокорреляции четвертого порядка

(связанной

с возможной сезонностью в квартальных данных)

(12.37)

нужно оценить регрессию

(12.38)

проверить нулевую гипотезу Н

=0.

Процедура одна и та же для авторегрессионной или

скользящей средней модели, генерирующей ошибки. Напри-

мер,

если ошибка описывается скользящей средней

то все равно

следует

оценить уравнение

(12.38)

и проверить

292

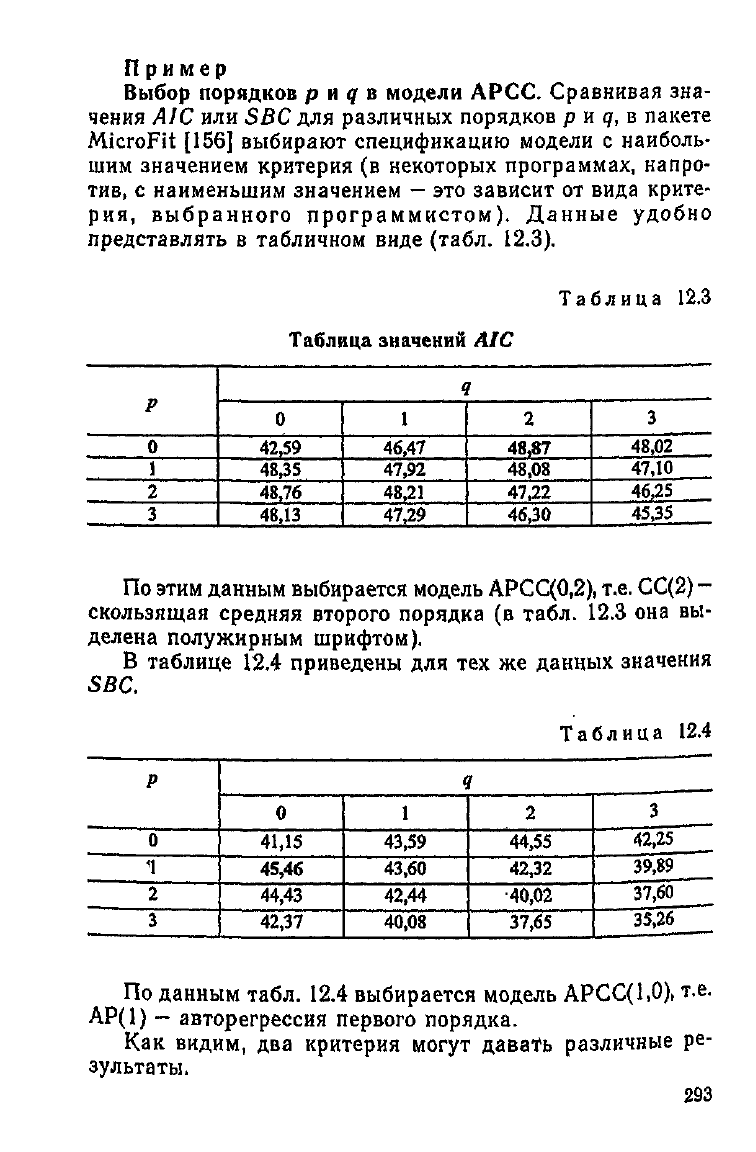
Пример

Выбор порядков р и q в модели АРСС.

Сравнивая зна-

чения

AIC

или

SBC

для различных порядков

р и

<7,

пакете

MicroFit

[156]

выбирают спецификацию модели

наиболь-

шим

значением критерия

(в

некоторых программах, напро-

тив,

наименьшим значением

—

это

зависит

от

вида крите-

рия,

выбранного программистом). Данные удобно

представлять

табличном виде (табл. 12.3).

Таблица

12.3

Таблица значений

42,59

48,35

48,76

48,13

46,47

47,92

48,21

47,29

AIC

48,87

48,08

47,22

46,30

48,02

47,10

46,25

45,35

По

этим данным выбирается модель АРСС(0,2), т.е.

СС(2)

скользящая средняя второго порядка

(в

табл.

12.3 она вы-

делена полужирным шрифтом).

В таблице

12.4

приведены

для тех же

данных значения

SBC.

Таблица

12.4

41,15

45,46

44,43

42,37

43,59

43,60

42,44

40,08

44,55

42,32

40,02

37,65

42,25

39,89

37,60

35,26

По

данным табл.

12.4

выбирается модель АРСС(1,0),

т.е.

АР(1)

—

авторегрессия первого порядка.

Как

видим,

два

критерия могут давать различные

ре-

зультаты.

293

Определение типа тренда, порядка разностей d. Тип

тренда во временном ряде может быть детерминированным

либо стохастическим. Тип тренда устанавливается с помо-

щью критерия ADF. Этот же критерий позволяет установить

порядок

разностей, обеспечивающий стационарность.

Рассмотрим, например, процесс АР{{)

где и распределены идентично и независимо, т.е. u-nd(0,a

Если

]ф|

то тренд детерминированный, а если

ф=

1, то имеет-

ся

единичный корень

первые разности стационарны, т.е. тренд

стохастический с ненулевым дрейфом аи d =1.

Попытка

определить тип тренда в общем виде принима-

ет форму проверки односторонней гипотезы о наличии еди-

ничного

корня против альтернативной гипотезы о стацио-

нарности

стохастического тренда:

ф = 1 против Н,:

< 1.

Важно отметить, что при использовании /-статистики для

проверки,

что

= 1 , критические значения нужно брать не

из

таблиц стандартного /-распределения, а из нестандарт-

ного распределения Дикки — Фуллера.

В более общем случае, когда возмущения u

, t =

1,2,...,

п,

автокоррелированы,

следует

применять расширенный кри-

терий Дикки — Фуллера для проверки наличия единичных

корней,

который предполагает

учесть

автокорреляцию ошиб-

ки

путем добавления лаговых разностей у,:

что может быть также записано как

где нулевая гипотеза теперь имеет вид Н

: р - 1 -

- 0.

ходе

проверки на наличие единичных корней необхо-

димо выбрать оптимальный порядок р регрессии ADF. Это

делается методом проб на основе критерия AIC или SBC.

294

Отметим, что к полученным первым разностям

следует

повторно применить критерий ADF с целью проверки, не

следует

ли перейти ко вторым разностям для обеспечения

стационарности и т.д., пока не

будет

определен порядок

интегрированности d. Напомним также, что критические зна-

чения

статистик Дикки — Фуллера зависят от включения в

уравнение свободного члена и временного тренда. Отметим,

что, например, в пакете MicroFit имеется специальная, по-

зволяющая проводить анализ наличия единичных корней

процедура, которая автоматически выводит и критические

значения

статистик Дикки — Фуллера.

Данная

глава

посвящена проблемам тренда во времен-

ном

ряде. Еще в гл. 1, § 1 были введены понятия детермини-

рованного и стохастического трендов. Теперь же рассмотре-

ны

критерии обнаружения трендов и установления их типа.

Материал этой главы весьма важен для построения моде-

лей Бокса - Дженкинса

KPWQC{p,d>q)>

рассмотренных нами

гл. 7, в частности, для определения необходимого порядка

разностей d. Это первый, но, очевидно, важнейший шаг в

построении моделей такого класса. Определение порядка

авторегрессии р и порядка скользящей средней q осуществ-

ляется с помощью информационного критерия Акайка (AIC)

или

байесовского критерия Шварца (SBC), которые имеют-

ся

в стандартных эконометрических пакетах программ, на-

пример в пакете MicroFit.

Глава

ИНТЕГРИРОВАННОСТЬ

КОИНТЕГРИРОВАННОСТЬ

ПЕРЕМЕННЫХ

В эконометрическом моделировании часто

тре-

буется

предварительное элиминирование временных трен-

дов из исходных данных. Кроме того, необходима сбаланси-

рованность динамических свойств переменных, стоящих

левой

правой частях регрессионного уравнения. Каким

образом осуществляется контроль

этом случае, мы

рас-

смотрим

этой главе.

§ 1.

ИНТЕГРИРОВАННОСТЬ

КОИНТЕГРИРОВАННОСТЬ

ДВУХ

ПЕРЕМЕННЫХ

Большинство экономических рядов нестационар-

но,

поскольку обычно

они

имеют линейный, параболичес-

кий

или экспоненциальный временной тренд. Однако часто

временной ряд можно привести к стационарному

виду,

если

перейти

его разностям (приростам) вида

У~У

Если пер-

вые разности ряда стационарны,

то

говорят,

что

этот

ряд

является

интегрированным первого

порядка.,

Переход

разностям приводит

потере ценной долгосрочной

инфор-

мации

данных. Сравнительно недавно

для

решения этой

проблемы были предложены понятия интегрированности

коинтегрированности временных рядов [142]. Несмотря

на

то

что

предположение

нормальности

независимости

не

является необходимым, дадим определения при этом пред-

положении.

296

Если

стационарный временной ряд

и~1Щ0,а

говорят,

что и, является интегрированным процессом порядка ноль

записывают это символически как /(0).

Если

генерирован моделью случайного блуждания

то,

приняв, что у

—

0, путем последовательных подстановок

получаем

Таким

образом, y

является суммой и., и

является процессом /(0). В этом

случае

говорят, что y

явля-

ется интегрированным процессом порядка один, т.е.

~I(l).

Если

//,

есть /(1) и мы прибавляем к нему z

, который

является /(0), то сумма (у

(

+ z

)

будет

/(1).

Когда специфицируют регрессионную модель для вре-

менных рядов, то обращают внимание на то, чтобы различ-

ные

переменные уравнения имели одинаковый порядок ин-

тегрированности, т.е.чтобы при одном порядке разности они

достигали стационарного вида. В противном

случае

урав-

нение

не имеет смысла. Например, если специфицируется

регрессионная модель

(13.1)

предполагается, что «/-INfO.c

), т.е. что u

является /(0), то

нужно удостовериться, что y

и x

являются интегрирован-

ными

процессами одного порядка. Например, если у, есть

/(1),

a x

~ процесс /(0), то ни при каком ß соотношение

(13.1)

не

будет

удовлетворено.

Пусть ^есть /(1) и х, тоже /(1),

тогда,

если

существует

такое ненулевое значение ß, что y

~ ßx, есть процесс /(0), то

говорят, что у, и x

коинтегрированы.

297

Предположим, что y

и x

являются процессами случай-

ного блуждания, так что оба они /(1). Тогда уравнение в

первых разностях вида

(13.2)

является правомерным, так как

Ах

(

, (y—^x

) и все и,

являются процессами /(0).

Уравнение

(13.1)

рассматривается как долгосрочное со-

отношение

между

и x

, а уравнение

(13.2)

описывает крат-

косрочную динамику. Энгл и Гренжер предлагают оцени-

вать выражение

(13.1)

методом наименьших квадратов,

получать оценку д и подставлять ее в уравнение

(13.2)

тем, чтобы затем получить оценки параметров

ос

и А,. Одна-

ко

эта

двухшаговая

процедура основывается на предполо-

жении,

что y

и х, коинтегрированы. Поэтому предваритель-

но

нужно проверить наличие коинтегрированности. Энгл и

Гренжер предлагают оценивать модель

(13.1)

МНК, полу-

чать остатки h

а затем применять критерий Дикки

—

Фул-

лера для анализа этих остатков. Целью данного теста явля-

ется проверка гипотезы, что р

1 в уравнении

т.е. проверка гипотезы Н

: u

~I(l). По

сути

дела,

проверяет-

ся

гипотеза, что y

и х, не коинтегрированы. Поскольку

у,~1(

х~[(1), мы хотим убедиться, что и. не является процессом

/(1).

Р.

Бьюли, М. Уиккенс и Т. Бройш [134, 162] показали, что

двухшаговая

процедура оценивания, предложенная Р. Энг-

лом и К. Гренжером, предполагающая сначала оценивание

параметра долгосрочной связи ß в уравнении (13.1), а затем

оценивание

параметров краткосрочной связи о и X в уравне-

нии

(13.2), не является необходимой. Они предлагают одно-

временное оценивание долгосрочных и краткосрочных пара-

метров, что позволяет получить более эффективные оценки

долгосрочного параметра р\ Разделив уравнение

(13.2)

на л.

немного перестроив уравнение, получаем

(13.3)

298

Поскольку

будет

коррелирована

ошибкой

урав-

нение

(13.3)

следует

оценивать методом инструментальной

переменной.

Коэффициенты

при Ay

и Ax

описывают крат-

косрочную динамику. Отметим,

что

если

(

и x

являются

/(1),

то Ay

и Ax

, как и a

есть /(0).

М.

Уиккенс

и Т.

Бройш

показали,

что ошибки

спецификации краткосрочной дина-

мики

не оказывают большого влияния

на

оценивание долго-

срочных параметров.

Например,

даже

если

уравнении

(13.3)

опущена

оценка параметра

будет

состоятельной.

§ 2. КОИНТЕГРАЦИЯ МНОГИХ

ПЕРЕМЕННЫХ

Итак,

простейших

случаях

стохастический тренд

переменной устраняется путем перехода

разностям. По-

лученный стационарный

ряд

может быть представлен

мо-

делью

АРИСС, оцененной

на

статистических данных.

Эта

идея может быть обобщена

на

случай множественного

рег-

рессионного анализа, когда

все

нестационарные ряды при-

ведены

стационарному

виду

путем перехода

разностям

соответствующего порядка. Однако

многомерном

случае

работа

нестационарными рядами

не

столь проста.

Определение

коинтеграции.

Переменные,

вхо-

дящие

регрессионную модель, должны находиться

неко-

тором равновесии, что означает наличие связи

между

их сто-

хастическими трендами. Формальный анализ начнем

рассмотрения множества экономических переменных

дол-

госрочном равновесии, когда

Если ввести вектора

х,~ (х

,...,

к1

)

ß« (ß,, ß

.»,

ß*)'»

то

векторном виде долгосрочное равновесие можно запи-

сать

как

где

=»

1,2,...,

п\

— объем выборки.

Отклонение

от

долгосрочного равновесия

«- x,ß

назо-

вем

ошибкой

равновесия.

Если равновесие

действитель-

299

ности

существует,

то ошибка равновесия должна быть ста-

ционарным

процессом. Р. Энгл и К. Гренжер в общем слу-

чае

дают

следующее

определение коинтеграции.

Говорят,

что компоненты вектора х,= (х

,...,

)

коин-

тегрированы порядка (d, b), что обозначается как x

~CJ(d,b),

если:

1) все компоненты вектора х, - интегрированные про-

цессы порядка d;

существует

вектор ß= (ß

, ..., ß

)' такой, что линей-

ная

комбинация

представляет собой интегрированный процесс порядка (d -

—

Ь),

где b > 0; вектор ß называется

вектором,

коинтеграции.

Следует

сделать четыре важных замечания относитель-

но

этого определения.

1. Понятие коинтеграции относится к линейной комби-

нации

нестационарных переменных. Теоретически вполне

возможно, что

существуют

нелинейные долгосрочные соот-

ношения

между

множеством интегрированных переменных.

Однако современная эконометрика не располагает крите-

риями

для проверки нелинейных коинтеграционных связей.

Отметим также, что вектор коинтеграции не единствен. Если

(ß,,

,...,

)' является таким вектором, то для любого отлич-

ного от нуля X вектор

(X,ß,,

Xß

,...,

XfiJ

также является векто-

ром коинтеграции. Поэтому обычно одна из переменных

используется для нормализации вектора коинтеграции пу-

тем приравнивания ее коэффициента единице. Для норма-

лизации

вектора коинтеграции относительно х

{

просто сле-

дует

взять Х- l/ß,.

2. Все коинтегрированные переменные должны иметь

одинаковый порядок интеграции (необходимое условие). Это,

конечно,

не означает, что все переменные одного порядка

интеграции являются коинтегрированными. Обычно как раз

наоборот.

Отсутствие

коинтеграции означает

отсутствие

долгосрочного равновесия в переменных, так что они

могут

уходить

сколь

угодно

далеко одна от другой. Однако, если

переменные имеют разные порядки интеграции, то они не

могут

быть коинтегрированы. Например, если

~l{d

~I(d

)

имеют разные порядки интеграции, т.е. d^t d

то

300