Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

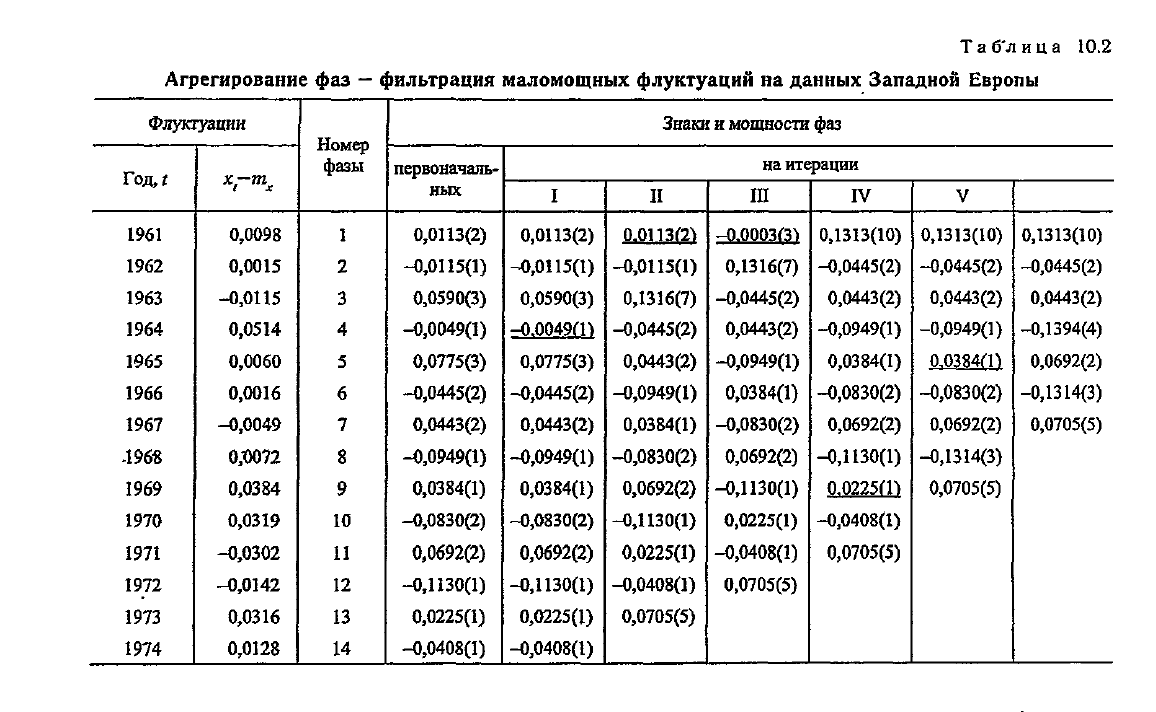
Таблица

10.2

Агрегирование фаз

—

фильтрация маломощных флуктуации на данных Западной Европы

Флуктуации

Год,*

1961

1962

1963

1964

1965

1966

1967

.196«

1969

1970

1971

1972

1973

1974

х,-т

0,0098

0,0015

-0,0115

0,0514

0,0060

0,0016

-0,0049

0ДЮ72

0,0384

0,0319

-0,0302

-0,0142

0,0316

0,0128

Номер

фазы

первоначаль-

ных

0,0113(2)

-0,0115(1)

0,0590(3)

-0,0049(1)

0,0775(3)

-0,0445(2)

0,0443(2)

-0,0949(1)

0,0384(1)

-0,0830(2)

0,0692(2)

-0,1130(1)

0,0225(1)

-0,0408(1)

Знаки

мощности

фаз

на

итерации

0,0113(2)

-0,0115(1)

0,0590(3)

-0.0049ГП

0,0775(3)

-0,0445(2)

0,0443(2)

-0,0949(1)

0,0384(1)

-0,0830(2)

0,0692(2)

-0,1130(1)

0,0225(1)

-0,0408(1)

0.0113^

-0,0115(1)

0,1316(7)

-0,0445(2)

0,0443(2)

-0,0949(1)

0,0384(1)

-0,0830(2)

0,0692(2)

-0,1130(1)

0,0225(1)

-0,0408(1)

0,0705(5)

III

-О.О0ОЗГ31

0,1316(7)

-0,0445(2)

0,0443(2)

-0,0949(1)

0,0384(1)

-0,0830(2)

0,0692(2)

-0,1130(1)

0,0225(1)

-0,0408(1)

0,0705(5)

0,1313(10)

-0,0445(2)

0,0443(2)

-0,0949(1)

0,0384(1)

-0,0830(2)

0,0692(2)

-0,1130(1)

0.0225Ш

-0,0408(1)

0,0705(5)

0,1313(10)

-0,0445(2)

0,0443(2)

-0,0949(1)

0.0384ГП

-0,0830(2)

0,0692(2)

-0,1314(3)

0,0705(5)

0,1313(10)

-0,0445(2)

0,0443(2)

-0,1394(4)

0,0692(2)

-0,1314(3)

0,0705(5)

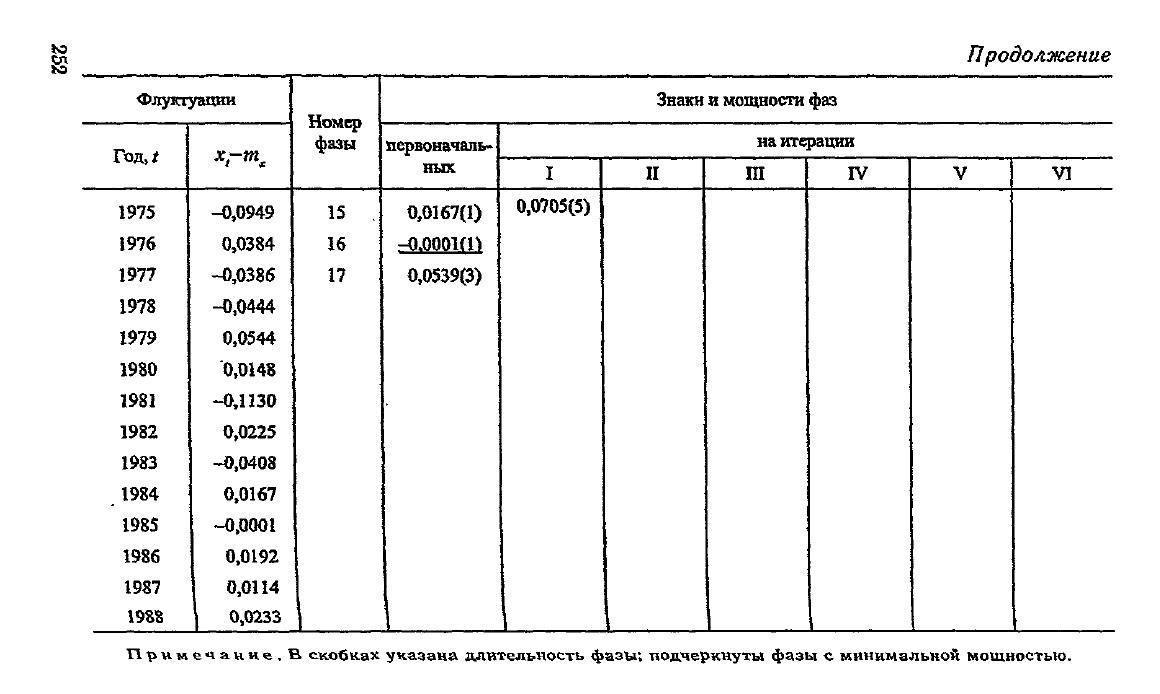
Продолжение

Флуктуации

Год,/

1975

1976

1977

1978

1979

1980

1981

1982

1983

1984

1985

1986

1987

1988

-0,0949

0,0384

-0,0386

-0,0444

0,0544

0,0148

-0,1130

0,0225

-0,0408

0,0167

-0,0001

0,0192

0,0114

0,0233

Номер

фазы

Знаки

и мощности фаз

первоначаль-

ных

0,0167(1)

-о.оооип

0,0539(3)

на итерации

0,0705(5)

Примечание. В скобках указана

длительность

фазы;

подчеркнуты

фазы с минимальной мощностью.

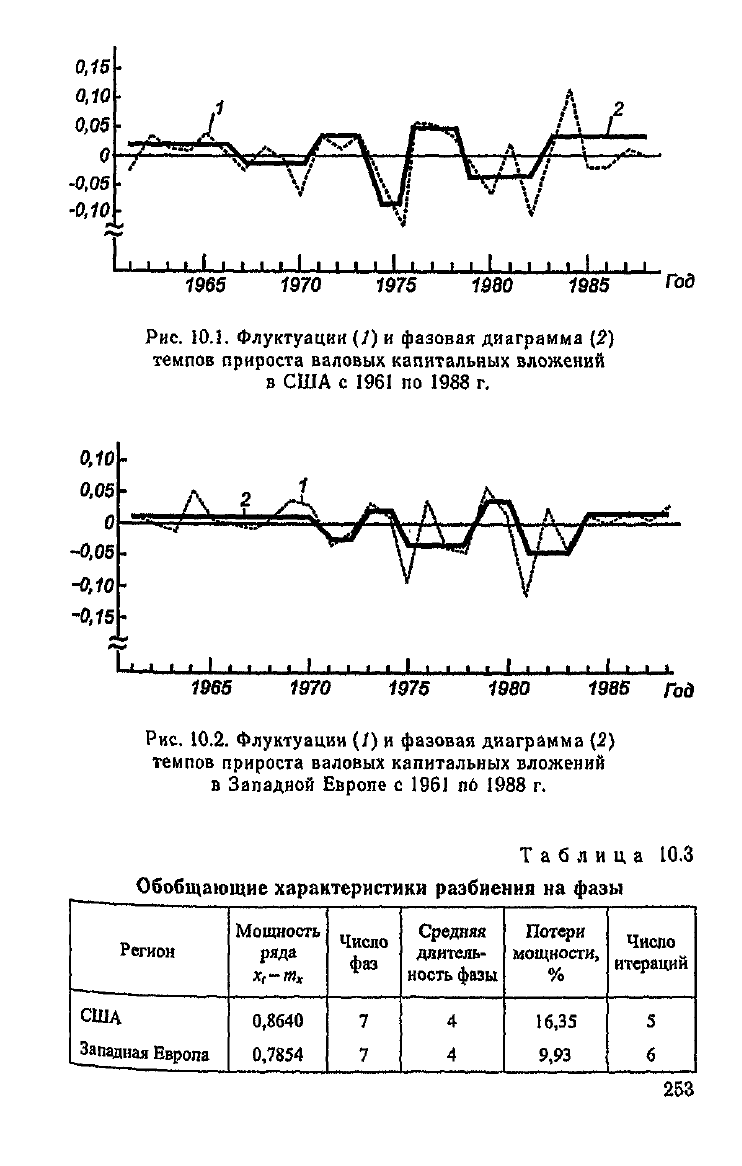
Рис.

ЮЛ. Флуктуации (/) и фазовая диаграмма (2)

темпов прироста валовых капитальных вложений

США с 1961 по 1988 г.

Рис.

10.2. Флуктуации (/) и фазовая диаграмма (2)

темпов прироста валовых капитальных вложений

Западной Европе с 1961 по 1988 г.

Таблица 10.3

Обобщающие характеристики разбиения на фазы

Регион

США

Западная

Европа

Мощность

ряда

х,

—

0,8640

0,7854

Число

фаз

Средняя

длитель-

ность

фазы

Потери

мощности,

16,35

9,93

Число

итераций

253

Рис.

10.3. Фазовые диаграммы темпов прироста

валовых капитальных вложений в США (/)

в Западной Европе (2) с 1961 по 1988 г.

Вследствие изменчивости лага формально рассчитанные

коэффициенты

лаговой корреляции не

могут

дать

столь на-

глядной картины развития

двух

процессов во времени, как

это демонстрируют фазовые диаграммы.

Применение

рассмотренного нами метода фазового ана-

лиза временных рядов

дает

возможность сохранить локаль-

ную индивидуальность нерегулярных циклических колебаний

последовательно переходить к анализу все более длинных

мощных волн, абстрагируясь от колебаний меньшего масш-

таба. Метод отличается простотой и ясностью концепции.

Анализ проводится во времени, что облегчает интерпре

тацию получаемых результатов, позволяет сопоставить их с

другими событиями окружающего мира. Обработка ряд

возможна с помощью универсальных электронных таблич-

ных процессоров типа Excel, Lotus 1-2-3 и т.п.

От исследователя требуется подготовка задачи к фазово-

му анализу, включая предварительное преобразование ис-

ходного ряда, определение уровня отсчета флуктуации, зада-

ние

критерия останова итеративного процесса агрегирования

фаз.

В остальном алгоритм носит жесткий, однозначный ха-

254

рактер

не зависит от желаний исследователя, поэтому можно

полагать, что рассмотренный фазовый анализ

дает

достаточ-

но

объективные результаты.

Достоинством метода является его способность выделять

локальные колебательные движения временного ряда и ис-

следовать их особенности, недостаток состоит в том, что ме-

ханизм, генерирующий колебания, остается неизученным. Для

его познания требуется построение гибкой многофакторной

модели [124], поэтому результаты, получаемые с помощью

фазового анализа временных рядов,

следует

рассматривать

как

исходные для более глубокого изучения колебательных

процессов.

Глава 11

АДАПТИВНАЯ ГИСТОГРАММА, ПРОБЛЕМА

ОПТИМИЗАЦИИ

Рассматриваются критерий и метод оптимиза-

ции

адаптивной процедуры последовательного обновления

гистограммы временного ряда, изложенной в гл. 2 §1. При-

водится пример использования адаптивной гистограммы для

анализа динамики распределения кассовых остатков в бан-

ковском

учреждении.

§ 1. ПОСТАНОВКА ПРОБЛЕМЫ

В анализе кассовых остатков банковского

учреж-

дения,

как и во многих

других

экономических

задачах,

час-

то требуется определить форму закона распределения ве-

роятностей случайной переменной. На практике для этих

целей используется построенная на выборочных данных до-

статочного объема гистограмма, показывающая эмпиричес-

кий

закон распределения.

Так,

если процесс, представляемый переменной, стацио-

нарен,

то такое решение задачи

следует

признать вполне

удовлетворительным. Однако гораздо чаще стохастический

процесс,

порождающий переменную, является нестационар-

ным

— изменяются его средний уровень, размах отклонений

от среднего, а также форма кривой распределения амплитуд

колебаний.

Если эти изменения носят эволюционный харак-

тер, то, как показал Р.Г. Браун [47], может быть построена

адаптивная процедура обновления гистограммы, основыва-

ющаяся на экспоненциальном сглаживании нуля или едини-

цы.

Эта процедура рассмотрена нами в гл. 2 § 1. Обновлен-

256

ные значения частостей на момент^ для разных диапазонов

значений

исследуемой переменной и определяют гистограм-

му, приближенно отражающую закон распределения.

Нерешенным,

однако, остался вопрос о критерии каче-

ства этой процедуры и об оптимальном значении парамет-

ра адаптации. Решение данного вопроса изложено в [123].

§ 2. АДАПТИВНАЯ ПРОЦЕДУРА ОБНОВЛЕНИЯ

ГИСТОГРАММЫ

Напомним,

что в общем

случае

рассматривает-

ся

полная система п несовместных событий, определенных

на

числовой оси с помощью п+1 границы

(ИЛ)

Событию, связанному с наблюдением х, в момент /,

соответствует

номер интервала k — такой, что Х

{

х,<,Х

который попадает наблюдённое значение. Предполага-

ем, что моменты наблюдения разделены равными проме-

жутками времени и t - 1,2, ..., Т. Оценку на момент t

вероятности наступления события k

будем

обозначать как

(11.2)

Разбиение

оси х на интервалы произведем, разделив весь

диапазон (Х

тах

-Х

тЫ

)

между

верхним и нижним значением х

на

п равных частей. В общем

случае

границы

могут

быть

заданы произвольно в зависимости от характера задачи и

Целей исследования.

Грубые

начальные оценки

(0),

k = 1, 2, ..., п, можно

получить, например, используя прошлые данные или на-

чальную часть выборки объемом Г,

Т как частость

(11.3)

где

чи

—

число точек из подвыборки

{х,},

-l,2,...,T

попавших в

интервал

{

х,£Х

257

Далее построим «-мерный вектор-столбец u(t), который

имеет

(я—

1)-нулевую

компоненту, а k-я компонента равна еди-

нице.

Предыдущие оценки п вероятностей можно рассматри-

вать как «-компонентный вектор-столбец p(t—1). Процесс пе-

ресмотра этих оценок с

учетом

текущей информации является

экспоненциальным

сглаживанием вектора u(t) по формуле

(11.4)

где а — константа из интервала 0 < сс< 1, параметр адапта-

ции,

определяющий скорость обновления оценок. Каж-

дая компонента вектора модифицируется экспоненци-

альным сглаживанием нуля или единицы.

Так

как p{t~ 1) — вектор вероятностей, то все его компо-

ненты

неотрицательны и их сумма должна быть точно рав-

на.единице.

Экспоненциальное сглаживание не'может сде-

лать компоненту отрицательной, и сумма полученных новых

оценок

компонент равна предыдущей сумме, т.е. единице:

(П.5)

Таким

образом, экспоненциальное сглаживание векто-

ра вероятностей

дает

обновленный вектор вероятностей.

§ 3. ПРОБЛЕМЫ ОПТИМАЛЬНОСТИ

АДАПТИВНОЙ ПРОЦЕДУРЫ

ОБНОВЛЕНИЯ ГИСТОГРАММЫ

Рассмотрим событие i. Если закон распределе-

ния

наблюденных значений х, не меняется, то математичес-

кое ожидание значения компоненты i вектора и(/), подлежа-

щего сглаживанию, точно равно действительной вероятности р,

наступления события i и математическое ожидание оценки

равно действительной вероятности:

268

(11.6)

Вероятность того, что придется сглаживать единицу,

равна р., а того, что сглаживать нуль, составляет 1—

р..

Легко

подсчитать, что компонента i вектора \\{t) характеризуется

дисперсией

(11.7)

Если к компоненте и, применить процедуру экспоненци-

ального сглаживания, то дисперсия получаемой на

выходе

экспоненциальной

средней выражается через дисперсию

входного потока по известной формуле

(П.8)

где а — постоянная сглаживания.

После подстановки

(11.7)

получим дисперсию оценки

вероятности наступления события i:

(Н.9)

Из

(11.9)

Р.Г. Браун

делает

вывод, что имеются два наи-

более предпочтительных способа конструирования системы

границ Х

, X

.... А_, при которой дисперсия оценки срав-

нительно невелика. Он предлагает устанавливать такие

границы событий, чтобы р, была либо очень большой (близ-

кой

к единице), либо очень маленькой (почти равной нулю).

Это обеспечит малое значение произведения

р/1—

)

и, сле-

довательно, низкую дисперсию оценок компонент вектора

вероятностей. Максимум дисперсии достигается при р,~ 0,5.

259

Однако подобные рассуждения слишком формальны, а

полученные рекомендации не

всегда

реализуемы. Если, на-

пример,

положить, что р.= 0,9, то на все остальные события

остается лишь 10% вероятности. Такое разбиение на собы-

тия,

конечно, возможно, если речь идет, например, о разде-

лении

стандартных и нестандартных ситуаций. Но при адап-

тивном анализе распределения вероятностей потребуется

построить границы, разделяющие числовую ось на 5—9 или

более событий. Тогда условие p

~ 1 становится неприемле-

мым по очевидным причинам. В этом

случае

целесообразно

потребовать, чтобы все оценки вероятностей имели равные

дисперсии

= const или одинаковое отношение стандарт-

ной

ошибки к оценке вероятности

о*//>,=>=

const.

В первом

случае

выдвинутое требование означает, что

(11.10)

или

(11.11)

Несмотря на то что здесь формально можно получить

два решения, годится лишь одно - то, которое меньше 0,5,

поскольку таких р, должно быть 5-9 или более.

Во втором

случае

(11.12)

или

(11.13)

откуда

(11.14)

Таким

образом, в обоих

случаях

приходим к одному и

тому же

выводу,

что для равенства дисперсий оценок о^или

коэффициентов

вариации oj/p, границы событий надо вы-

бирать так, чтобы вероятности наступления этих событий

были одинаковыми.

260