Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

знать несостоятельной. Арифметическое усреднение по вре-

мени

дает

лишь весьма

грубый

результат,

ничего не говоря-

щий

о движении коэффициента корреляции во времени.

Поэтому в [122] и [125] предложен еще один, рекуррентный

(или

адаптивный), коэффициент корреляции

(9.2)

Как

видим, s

и d

являются экспоненциально-взвешен-

ными

скользящими средними произведений приростов и аб-

солютных произведений приростов

двух

рядов. Параметр а

—

постоянная

сглаживания или параметр адаптации (гл.

§2).

Ясно,

что и здесь -1 £ r

(a) й 1. График r

(a) относительно

времени показывает, как изменяется сила корреляционной

связи на выборочном' периоде. Открытым остается лишь воп-

рос о начальных значениях s

и d

, необходимых для начала

рекуррентной процедуры, и величине постоянной сглажи-

вания

а.

Начальные значения s

и d

предлагаем определять как

простые арифметические средние произведений и абсолют-

ных значений произведений приростов, вычисляемые на осно-

ве Г

наиболее ранних наблюдений выборки, 0 < T

Т-1.

Тогда

* s

/rf

будет

начальным коэффициентом корреля-

ции,

совпадающим с модифицированным коэффициентом кор-

реляции,

рассчитанным по (9.1) при Т

Т~ Величина а может

выбираться из указанного диапазона [0, 1], исходя из конкрет-

ного применения вычисляемого коэффициента корреляции.

Если вычисление такого коэффициента ставится как са-

мостоятельная задача, то можно предложить следующий

способ определения наилучшего а, Будем рассматривать

,_|(«)как прогноз совпадения колеблемости рядов л:,, и х

й1

момент t, a

(9.3)

231

как

ошибку этого прогноза на тот же момент. Тогда можно

ввести функцию потерь Q^cc)

(9.4)

где v=l или 2, и определять оптимальное значение а путем

минимизации

функции

(oc)

по а. Минимум легко найти

методом проб различных а из интервала [0, 1]. При необхо-

димости точно так же методом проб устанавливается и наи-

лучшее

значение Т

. В этом

случае

функция потерь рас-

сматривается как функция

двух

переменных

a).

Возможен и

другой

вариант адаптивного коэффициента

корреляции

(9.5)

здесь в качестве г

можно взять отношение г

~ с

/ q

где

Такой

коэффициент назовем

адаптивным

коэффициен-

том

знаковой

корреляции

приростов.

Далее, если действо-

вать так же, как и в предыдущем случае, нетрудно вычис-

лить ошибки e

и построить критерий

а), используя

(9.4) и (9.5). Оптимальные значения Т

и а

будуг

соответ-

ствовать минимуму Q.

§ 5. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ОТКЛОНЕНИЙ

ОТ ЗАДАННЫХ УРОВНЕЙ

В классическом корреляционном анализе отсчет

отклонений

переменной ведется от математического ожида-

ния.

Однако на практике такое отклонение представляет

интерес лишь в частных

случаях.

В экономических исследо-

232

ваниях, например, гораздо чаще важен знак отклонения от

предыдущего значения ряда (т.е. знак приращения) или от

нулевого уровня. Тогда и отклонения целесообразно рас-

сматривать от соответствующих величин.

Вообще говоря, в зависимости от задачи анализу

могут

подвергаться отклонения от моды, медианы, от какого-либо

заданного уровня. Назовем такой уровень критическим,

подразумевая под этим, что отклонения от него в разные

стороны имеют существенные качественные различия. Обо-

значим такой уровень для ряда x

через Е

. Пусть в этом

случае

требуется установить,

существует

ли взаимосвязь

между

отклонениями одной переменной, например (я,

—

с отклонениями

другой

—

), и если

существует,

то на-

сколько она сильна.

Возьмем в качестве измерителя корреляционной связи в

этом

случае

коэффициент

(9.6)

рассмотрим его свойства. Совершенно

ясно,

что он нахо-

дится в обычных пределах -1 й г

<, 1. Его оценкой может

служить корреляционный коэффициент:

(9.7)

Если Е

= 0 и Е

«= 0, то коэффициент г

характеризует

силу взаимосвязи

между

отклонениями соответствующих пе-

ременных от нуля. При Е

- x

{

и Е

« г

получаем рассмот-

ренный выше модифицированный коэффициент корреляции,

который также можно назвать

коэффициентом

корреляции

приростов.

Отметим, однако, что при Е

= М(х) и Е

M(z),

где М — символ математического ожидания, коэффициент г

не идентичен классическому коэффициенту корреляции из-за

различных нормирующих множителей (знаменателей).

Никаких

ограничений для использования корреляцион-

ного коэффициента (9.7) нет. Он применим для переменных,

имеющих смещенное (когда Е

* М(х)) и несимметричное

233

распределение относительно критического уровня Е

. Одна-

ко

стационарность и эргодичность переменных предполага-

ются. Если же эти предположения слишком сильные, мож-

но

построить адаптивный коэффициент корреляции по

аналогии с (9.2), где приращения

следует

заменить на от-

клонения

от критических значений.

§ 6. УСЛОВНЫЙ

КОЭФФИЦИЕНТ

КОРРЕЛЯЦИИ

Рассмотренные коэффициенты корреляции отра-

жают

силу взаимосвязи колебаний

двух

рядов в целом. Та-

кая

характеристика может оказаться слишком общей и не

всегда

удовлетворит исследователя. Поставим вопрос

конк-

ретнее: насколько сильна связь, например, положительных

отклонений

(

с отклонениями z

? Для ее измерения введем

понятие

условного

коэффициента

корреляции.

Определим

его как

(9.8)

где суммируются только те произведения, в которых x

£ Е

Точно так же можно вычислить коэффициент взаимосвязи

отрицательных отклонений ряда x

с отклонением z

. Есте-

ственно,

что в обоих

случаях

коэффициенты корреляции

могут

принимать неодинаковые значения. Таким образом,

особенности взаимосвязи

двух

рядов теперь не скрываются

за одним-единственным значением коэффициента корреля-

ции,

как это предполагается в классической теории, а пред-

ставляются более дробно двумя коэффициентами.

Преимущества такого

подхода

наиболее ярко проявля-

ются

тогда,

когда одна переменная (например, x

) является

контролируемой, а

другая

) - непосредственно недоступ-

ной,

но коррелированной с первой. Тогда можно

«нащупать»

такое критическое значение Е

, при котором удерживание

х,

в области Е

й х

(

(или х, £ £,) имело бы наиболее благо-

приятные

последствия (т.е. наибольшее значение

коэффи-

циента корреляции) для удержания z

в пределах z

£ Е

(или,

наоборот, z

£ Е

234

В общем виде условия при вычислении коэффициента

корреляции

могут,

конечно, иметь произвольный вид

(9.9)

лишь бы хватило статистических данных для получения ус-

тойчивых оценок коэффициентов.

Доводом в пользу применения условного коэффициента

корреляции

(9.9)

могут

служить следующие рассуждения.

При

низких значениях амплитуды отклонений корреляци-

онная

связь может не просматриваться из-за влияния слу-

чайных помех, т.е. быть несущественной. А при больших

отклонениях определенность этой связи возрастает почти

до детерминированности. Тогда при большой амплитуде

отклонений

одной переменной резко возрастает степень пре-

допределенности области нахождения (например, знак при-

роста) второй переменной.

Легче

определить и лаг (запаз-

дывание во времени) одной переменной относительно другой.

Можно

считать, что в этом

случае

возрастает мощность

критерия.

Задавая значения А и В, можно выделить

любую

инте-

ресующую

нас область амплитуд отклонений первой пере-

менной

- Е

) и вычислить коэффициент корреляции с

переменной z

для этой области. Такой

подход

открывает

путь

к доскональному изучению взаимосвязи рядов, выяв-

лению специфических локальных корреляционных свойств.

Можно

сказать, что корреляционные свойства предстают в

«расщепленном» виде - их выражает множество

коэффи-

циентов.

§ 7.

ВЕРОЯТНОСТНЫЙ

КОЭФФИЦИЕНТ

КОРРЕЛЯЦИИ

Рассмотрим еще один метод исследования силы

сопряженности

двух

переменных на основе оценки услов-

ной

вероятности их связи [125]. Определим коэффициент кор-

реляции

как

235

(9.10)

где/?

—

вероятность того, что С £ г

(

— Е

<, D при условии

£ х,~ Е

<: В. Отсюда

следует,

что областью суще-

ствования коэффициента корреляции

будет

отрезок

(О,

1]. Она отличается от области существования рас-

смотренных выше

коэффициентов

корреляции, которая

охватывает отрезок [—1, 1].

Определение

(9.10)

теоретическое. Практическую оцен-

ку на основе статистических данных можно получить как

отношение

(9.11)

где я

- число наблюдений, когда z

- Е

оказывалось в пре-

делах

С £ 2, -

£D

при А

<,В;

- общее

число наблюдений в выборке, удовлетворяющих ус-

ловию

Айх

(

—

йВ.

Обратное направление связи характеризуется вели-

чиной

(9.12)

Здесь обозначения аналогичны использованным в (9,11).

Отсюда очевидно, что в общем

случае

(9.13)

Этот вид корреляционного коэффициента позволяет ис-

следовать взаимосвязь переменных с вероятностной точки

зрения

и найти диапазоны отклонений переменных, взаимо-

связь между которыми наблюдается с наибольшей вероят-

ностью.

236

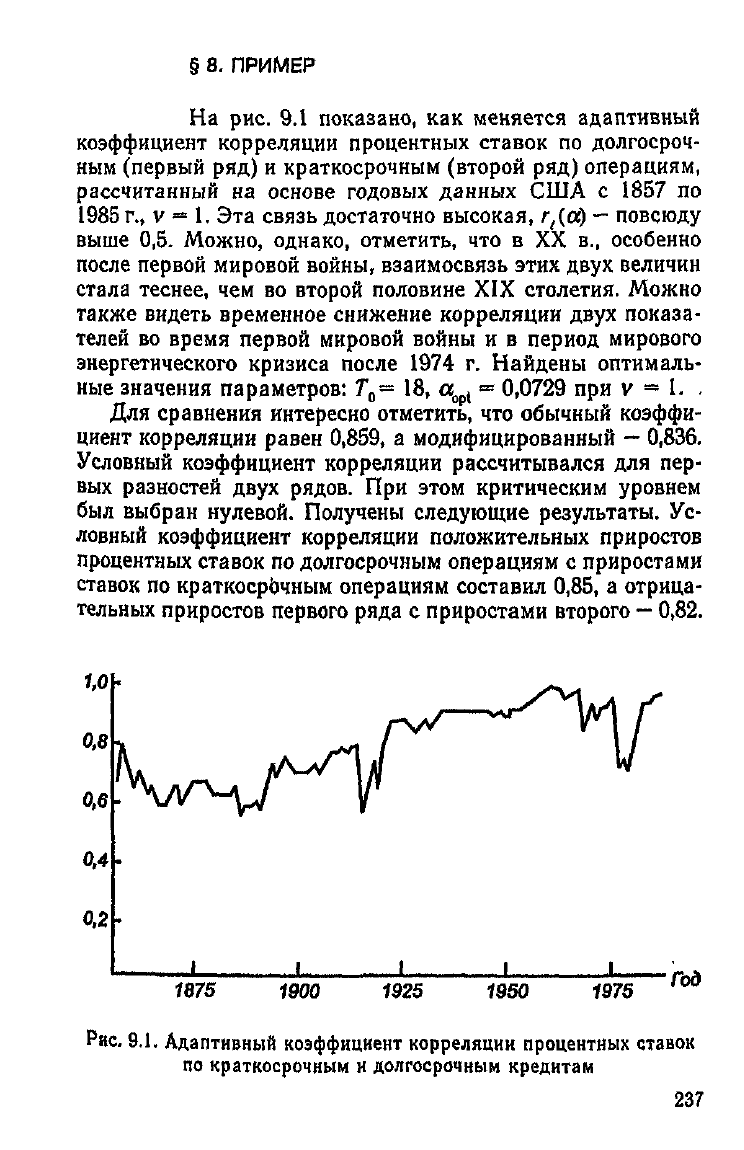
§ 8. ПРИМЕР

На

рис. 9.1 показано, как меняется адаптивный

коэффициент

корреляции процентных ставок по долгосроч-

ным

(первый ряд) и краткосрочным (второй ряд) операциям,

рассчитанный на основе

годовых

данных США с 1857 по

1985 г., v = 1. Эта связь достаточно высокая, гДа)

—

повсюду

выше 0,5. Можно, однако, отметить, что в XX в., особенно

после первой мировой войны, взаимосвязь этих

двух

величин

стала теснее, чем во второй половине XIX столетия. Можно

также видеть временное снижение корреляции

двух

показа-

телей во время первой мировой войны и в период мирового

энергетического кризиса после 1974 г. Найдены оптималь-

ные значения параметров: Т

= 18, а

ор1

0,0729

при V = 1.

Для сравнения интересно отметить, что обычный

коэффи-

циент корреляции равен

0,859,

а модифицированный

—

0,836.

Условный коэффициент корреляции рассчитывался для пер-

вых разностей

двух

рядов. При этом критическим уровнем

был выбран нулевой. Получены следующие результаты. Ус-

ловный коэффициент корреляции положительных приростов

процентных ставок по долгосрочным операциям с приростами

ставок по краткосрочным операциям составил 0,85, а отрица-

тельных приростов первого ряда с приростами второго

—

0,82.

Рис.

9.1,

Адаптивный

коэффициент корреляции процентных ставок

по краткосрочным и

долгосрочным

кредитам

237

Это

свидетельствует

о приблизительно одинаковой силе связи

падений и подъемов первого ряда с колебаниями второго.

Вероятностный коэффициент корреляции положительных

приростов первого ряда с положительными приростами вто-

рого равен 0,79, а отрицательных с отрицательными

—

только

0,64. Как видим, вероятность совпадения подъемов несколько

выше вероятности совместного снижения рассматриваемых

процентных ставок.

Вычисление условных коэффициентов автокорреляции со-

седних приростов (т= 1) дало следующие результаты. У пер-

вого ряда корреляционная связь положительного текущего

прироста с

будущим

приростом характеризуется коэффици-

ентом 0,52, а текущего отрицательного прироста с

будущим

приростом

—

0,41. Таким образом, положительные приросты

первого ряда позволяют строить более точные прогнозы на

будущее,

чем отрицательные. Аналогичные

коэффициенты

для

второго ряда соответственно равны —0,21 и 0,08, т.е. связь

последовательных приростов у процентных ставок по кратко-

срочным операциям совершенно незначительна.

Вероятностные коэффициенты автокорреляции прирос-

тов позволяют сделать такие выводы. Положительные

теку-

щие приросты первого ряда

влекут

за собой положитель-

ные приросты этого же ряда с вероятностью 52,6% (г =0,526),

а отрицательные с вероятностью 60,6% (г

0,606)

сопро-

вождаются также отрицательными приростами. Это может

быть использовано для прогнозирования знака прироста.

Для второго ряда аналогичные коэффициенты равны

0,549

0,429.

Здесь возможности для прогнозирования знака при-

роста меньше, поскольку появление в ближайшем

будущем

того или иного знака почти равновероятно.

Сделаем некоторые выводы. Введенные определения кор-

реляционных коэффициентов обладают рядом достоинств по

сравнению с классическим, но, разумеется, не претендуют

на

то, чтобы полностью заменить собой последнее. Напро-

тив,

в каждой конкретной задаче нужно использовать тот

тип корреляционного

коэффициента,

который наиболее адек-

ватен поставленной цели.

В предложенном модифицированном коэффициенте кор-

реляции

учитываются приращения переменных вместе с их

238

знаком.

Это равносильно

тому,

что вместо отклонений от ма-

тематического ожидания здесь рассматриваются отклонения

от ранее достигнутых значений. Идея отказа от математичес-

кого ожидания как от уровня отсчета отклонений и замены

его на некоторый критический (в сущности, произвольный, за-

данный

исследователем) уровень нашла себе применение и в

других

рассмотренных нами определениях. Адаптивный

коэф-

фициент

корреляции позволяет прослеживать динамику кор-

реляционной

связи во времени. Для исследования корреля-

ции

знаков приращений переменных построен адаптивный

коэффициент

знаковой корреляции. Практическое использо-

вание этого

подхода

для краткосрочного прогнозирования ва-

лютных курсов освещено в [126]. Этот метод может, конечно,

применяться

и на рынке ценных

бумаг.

Условный коэффициент корреляции, как и вероятност-

ный^

можно назвать

парциальными

коэффициентами

кор-

реляции,

так как они способны отражать частичные свой-

ства

двух

исследуемых временных рядов, наблюдаемые при

определенных условиях. Два последних

подхода

позволяют

проводить дифференцированный анализ взаимосвязи пере-

менных, выявлять, переходя от одного диапазона амплитуд

отклонений

другому,

неоднородность связи в разных под-

диапазонах и давать более

богатую

информацию исследо-

вателю для размышления и использования в аналитичес-

кой

и прогнозной деятельности. При необходимости

могут

быть построены адаптивные варианты этих коэффициентов.

Одной из перспективных областей применения подобных

подходов является построение

переключающихся

моделей,

т.е.

моделей с переключением в критические моменты времени с

одного режима работы на другой. Каждый режим можно пред-

ставить в модели специальным регрессионным уравнением, а

для определения критических моментов переключения режи-

мов целесообразно проводить предварительный корреляцион-

ный

анализ. В качестве критических моментов выступают

моменты, когда переменная пересекает (в наших обозначена

ях) уровень Е

, А или В.

Рассмотренные подходы, объединенные общим названи-

ем -

нетрадиционный

корреляционный

анализ,

дают

воз-

можность получать значительно более подробную инфор-

мацию о взаимосвязях переменных, чем это предлагает

классическая теория, и открывают новые перспективы в по-

знании

сложных динамических систем.

Глава 10

ФАЗОВЫЙ

АНАЛИЗ

ВРЕМЕННЫХ

РЯДОВ

Рассматривается

подход

к анализу нерегуляр-

ных циклических колебаний временных рядов, теоретичес-

кие

и методологические основы для изучения этих колеба-

ний

по фазам циклов, предложенные в [129]. Описан анализ

циклических колебаний на примере инвестиционных про-

цессов в США и странах Западной Европы,

§ 1. ПОСТАНОВКА ПРОБЛЕМЫ

В экономических исследованиях часто встречаются

показатели, движение которых во времени представляет со-

бой нерегулярные циклические колебания с переменной ам-

плитудой и неустойчивым периодом. Внешне стохастический

характер этих явлений отражает циклическое развитие эко-

номики

в условиях влияния на нее многих случайных, рыноч-

ных и волевых, управляющих воздействий.

Исследование фаз движения упомянутых показателей

традиционными методами, такими, как спектральный и рег-

рессионный

анализ, по ряду причин не подходит. Так, спек-

тральный метод аппроксимирует движение временного ряда,

отражающего движение того или иного показателя, суммой

регулярных синусоид. Между тем строгой периодичности и

постоянства амплитуды от экономических показателей

труд-

но

ожидать, поэтому для хорошей аппроксимации

требует-

ся

большое число синусоид различной частоты. Возникают

Трудности и с интерпретацией результатов [120]. Регресси-

онный

метод аппроксимирует всю выборку в целом, и ло-

кальные свойства ряда при этом играют второстепенную

240