Лубенцова В.С. Математические модели и методы в логистике
Подождите немного. Документ загружается.


50
первого.
Поздний срок наступления события i определяется по формуле:
(
)
(
)
(
)
пп
min,
titjtij
=−
(4.2)
для всех работ
(
)
,
ij
. Определение поздних сроков наступления со-
бытий начинается с
in
=
, где
n
– номер завершающего события се-
тевого графика. При этом принимаем
(
)
(
)
п p
tntn
= , а поздние сроки
определяются по формуле (4.2) в порядке убывания номеров собы-
тий.
После того, как найдены ранние и поздние сроки наступления
событий сетевого графика, можно определить критические работы,
образующие один или несколько критических путей. Работа является
критической, если временные параметры её начального и конечного
события удовлетворяют следующим трем условиям:
(
)
(
)
() ()
() () () () ( )
п
п
пп
,
,
,.
p
p
pp
titi
tjtj
tjtitjtitij
=
=
−=−=
(4.3)
Работа сетевого графика характеризуется следующими времен-
ными параметрами:
– ранний срок начала работы равен раннему сроку свершения её
начального события:
(
)
(
)
рнр
,
tijti
= ; (4.4)
– поздний срок окончания работы равен позднему сроку свер-
шения её конечного события:
(
)
(
)
пнп
,
tijtj
= ; (4.5)
– поздний срок начала работы равен позднему сроку ее оконча-
ния минус ее продолжительность:
(
)
(
)
(
)
пнп
,,
tijtjtij
=−; (4.6)
– ранний срок окончания работы равен раннему сроку начала
работы плюс ее продолжительность:
(
)
(
)
(
)
рор
,,
tijtitij
=+ . (4.7)
Полный резерв времени – это максимально возможный запас
времени для выполнения данной работы сверх продолжительности
самой работы при условии, что в результате такой задержки конеч-
ное для данной работы событие наступит не позднее, чем в свой
51
поздний срок:
(
)
(
)
(
)
(
)
ппр
,,
Rijtjtitij
=−− . (4.8)
Свободный резерв времени – это запас времени, которым можно
располагать при выполнении данной работы в предположении, что
предшествующее и последующее события этой работы наступают в
свои самые ранние сроки:
(
)
(
)
(
)
(
)
рр
,,
c
Rijtjtitij
=−− . (4.9)
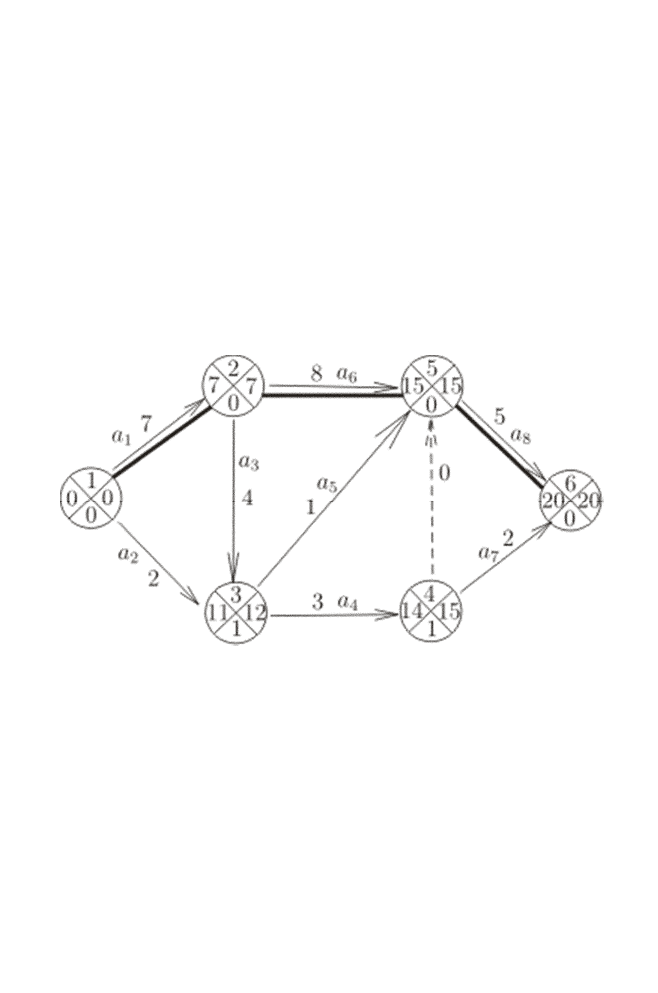
Рассмотрим сетевую модель. Пусть какой-то комплекс работ
реализуется графом. Продолжительности выполнения каждой работы
даны у стрелок. Определим временные параметры событий и найдем
критический путь сетевого графика (рис. 4.4). Здесь а
i
– необходи-
мые ресурсы.
Р и с. 4.4. Сетевой график
Все необходимые расчеты выполним непосредственно, пользу-
ясь рисунком. Кружки, соответствующие событиям, разделим на 4
сегмента, в верхнем будем писать номер
i
события, в левом –
(
)
р
ti
,
в правом –
(
)
п
ti
, а в нижнем – резерв времени события:
(
)
(
)
(
)
пр
Rititi
=−. (4.10)
Решение начинаем с нумерации событий в соответствии с пра-
вилами, приведёнными выше. Далее определяем ранние сроки на-
ступления события, начиная с исходного, для которого полагаем
(
)
р
10
t
=
.
Переходим к событию 2. В него входит только одна работа

52
(1, 2), поэтому:
(
)
(
)
(
)
рр
211,27
ttt
=+=
.
В событие 3 входят 2 работы, поэтому:
(
)
(
)
(
)
(
)
(
)
рр
1,2
3max,3max02,7411
i
ttiti
=
=+=++=
,
(
)
(
)
(
)
рр
433,411314
ttt
=+=+=
,
(
)
(
)
(
)
(
)
(
)
(
)
рр
2,3,4
5max,5max78,111,14015
i
ttiti
=
=+=+++=
,
(
)
(
)
(
)
(
)
(
)
рр
4,5
6max,6max142,15520
i
ttiti
=
=+=++=
.
Определяем поздние сроки наступления событий, начиная с за-
вершающего.
Полагаем
(
)
(
)
пр
6620
tt
==
,
(
)
(
)
(
)
пп
565,615
ttt
=+=
,
(
)
(
)
(
)
(
)
(
)
пп
5,6
4min4,min150,20215
i
ttjtj
=
=−=−−=
,
(
)
(
)
(
)
(
)
(
)
пп
4,5
3min3,min153,15112
i
ttjtj
=
=−=−−=
,
(
)
(
)
(
)
(
)
(
)
пп
3,5
2min2,min124,1587
i
ttjtj
=
=−=−−=
,
(
)
(
)
(
)
(
)
(
)
пп
2,3
1min1,min77,1520
i
ttjtj
=
=−=−−=
.
Условиям (4.З) соответствуют работы (1,2), (2,5) и (5,6). Эти ра-
боты являются критическими и образуют критический путь сетевого
графика, соединяющий исходное событие с завершающим и опреде-
ляющий продолжительность работ всего комплекса.
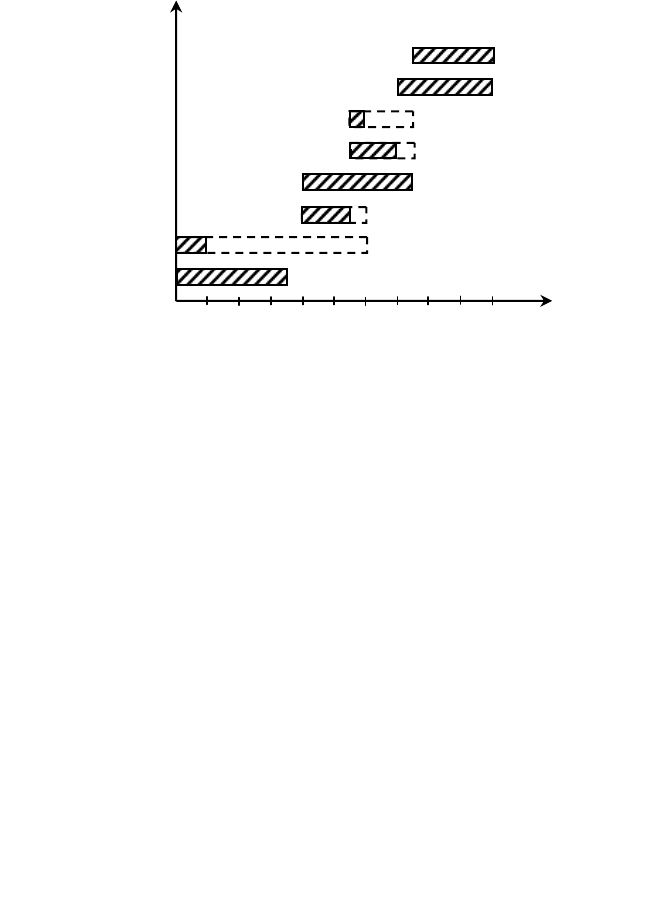
Сетевой график дает четкое представление о взаимосвязи работ
и порядке их следования, однако он неудобен для определения со-
става работ, который должен выполняться в каждый момент време-
ни. Поэтому рекомендуется после расчета временных параметров
сетевого графика построить линейный график выполнения работ,
каждая из которых изображается параллельным оси времени отрез-
ком. Длина отрезка равна продолжительности выполнения работы.
Время, в пределах которого могут выполняться некритические рабо-
ты, показывается пунктиром. Линейный график выполнения работ
имеет вид, представленный на рис. 4.5.
53
Сетевые методы анализа и управления позволяют упорядочивать
работы комплекса таким образом, что в конечном счете комплекс
будет завершен при условии соблюдения данной последовательности
выполнения работ. Кроме того, для выполнения комплекса работ не-
обходимы ресурсы, наличие которых гарантирует физическую ре-
альность комплекса. Ресурсы, как правило, ограничены, вследствие
чего на последовательность выполнения работ накладываются до-
полнительные ограничения, связанные с наличием свободных ресур-
сов в данный момент времени.
Определение временных параметров и работ, нахождение кри-
тического пути сетевого графика – это только часть планирования,
следующим этапом является проверка физической реализуемости
проекта.
Отправной точкой этого этапа является определение общей по-
требности в ресурсах для каждого единичного интервала времени.
Для решения этой задачи лучше всего воспользоваться, линейным
графиком выполнения работ с указанием потребности каждой рабо-
ты в необходимых ресурсах.
Процедура распределения ресурсов заключается в планировании
начала выполнения работы в соответствии с условиями предшество-
вания и наличием свободных ресурсов.
(5,6)
(4,6)
(3,5)
(3,4)
(2,5)
(2,3)
(1,3)
(1,2)
работа
t
2 4 6 8 10 12 14 16 18 20
Р и с. 4.5

54
4.3. Распределение ограниченных ресурсов
при построении сетевого графика. Последовательный метод
При построении сетевого графика необходимо учитывать нали-
чие ресурсов, т.к. одновременное выполнение некоторых операций
из-за ограничений, связанных с рабочей силой, оборудованием и
другими видами ресурсов иногда оказывается невозможным. Именно
в этом отношении представляют ценность полные резервы времени
некритических операций. Сдвигая некритическую операцию в том
или ином направлении, но в пределах её полного резерва времени,
можно добиться снижения максимальной потребности в ресурсах.
Однако даже при отсутствии ограничений на ресурсы полные резер-
вы времени обычно используются для выравнивания потребностей в
ресурсах на протяжении всего срока реализации программы работ.
Это означает, что работы удастся выполнить более или менее посто-
янным составом рабочей силы.
Процедура распределения ресурсов заключается в планировании
начала выполнения работ, в соответствии с условиями предшество-
вания и наличием свободных ресурсов. Для реализации этой проце-
дуры разработано несколько методов. Одним из основных является
последовательный метод.
Суть метода заключается в том, что ресурсы, выделенные для
выполнения работы, закрепляются за этой работой до её окончания.
Ограниченность ресурсов приводит к тому, что не все работы, нача-
ло которых возможно, могут быть начаты одновременно. В подоб-
ных ситуациях необходимы критерии, позволяющие отдать предпоч-
тение той или иной работе. Соображения, определяющие принимае-
мые решения, могут быть сформулированы как следующее правила
предпочтения:
1) направить ресурсы на выполнение работы, имеющей наи-
меньший полный резерв времени (при прочих равных условиях);
2) направить ресурсы на выполнение работы, имеющей наи-
большее число ресурсо-дней (при прочих равных условиях);
3) направить ресурсы на выполнение работы, использующей
наибольшее количество ресурсов (при прочих равных условиях);
4) направить ресурсы на выполнение работы с меньшим номе-
ром.
При этом необходим контроль времени, в течение которого по-
требление ресурсов соответствует их плановому распределению. Так
55
как ресурсы закрепляются за работой на весь срок её выполнения, то
изменение количества свободных ресурсов будет происходить в дис-
кретные моменты времени, соответствующие окончанию той или
иной работы.
Для фиксации таких моментов введём понятие текущего време-
ни. В начальный момент значение текущего времени принимается
равным нулю. Затем текущее время становится равным времени
окончания первой работы, второй и т.д.
В связи с этим может быть предложена следующая последова-
тельность распределения ресурсов. Формируется список работ, кото-
рые могут быть начаты по условиям предшествования. В соответст-
вии с правилами предпочтение для этих работ определяются приори-
теты, указывающие, в какой последовательности распределяются
свободные ресурсы. Работы, для которых были выделены ресурсы,
фиксируются как выполняемые, и среди них находится та, которая
будет закончена раньше всех остальных. Время окончания этой ра-
боты определяет новое значение текущего времени, а свободные ре-
сурсы пополняются за счет высвободившихся ресурсов. При каждом
измерении текущего времени производится корректировка времен-
ных параметров работ, после чего множество работ, которые могут
быть начаты, пополняется за счёт работ, ранние сроки которых рав-
ны текущему времени, а из множества выполняемых работ исключа-
ется выполненная. Описанная процедура циклически повторяется до
тех пор, пока все работы не будут выполнены. Время окончания по-
следней работы определяет время выполнения всего комплекса.
Рассмотрим, например, сетевой график, для которого был най-
ден критический путь 1–2–5–6 (рис. 4.6).
Р и с. 4.6. Критический путь

56
Задача распределения ресурсов может быть сформулирована
двояко:
1) определить время выполнения всего комплекса работ при за-
данном количестве ресурсов;
2) определить необходимое количество ресурсов для выполне-
ния комплекса работ в заданные сроки.
В любой постановке рассматриваемой задачи решение должно
начинаться с определения разумного начального приближения.
Поступим следующим образом. Определим ресурсо-дни для ка-
ждой работы и просуммируем. Найденную сумму разделим на дли-
тельность выполнения комплекса, в результате чего получим среднее
число единиц ресурса, необходимое ежедневно. При этом следует
учитывать два момента:
– во-первых, полученное число должно быть целым, поскольку
ресурсы (люди, машины) измеряются, как правило, только целыми
числами;
– во-вторых, среднее число требуемых ресурсов должно быть не
меньше, чем потребность в них любой работы, иначе некоторые ра-
боты никогда не смогут быть выполнены.
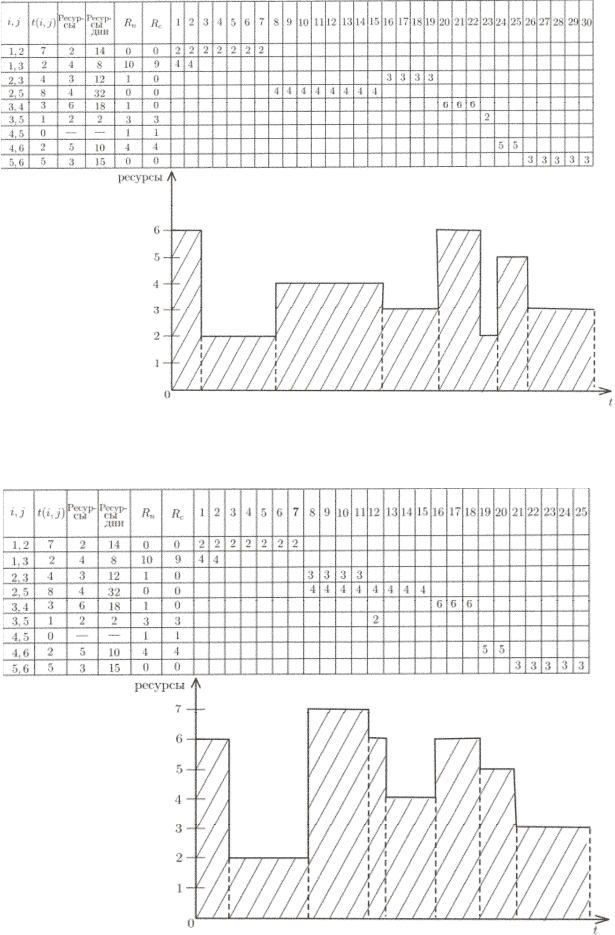
В рассматриваемом примере минимальное число ресурсов (лю-
дей), необходимых для выполнения комплекса работ, в первом при-
ближении равно 111/20=5,5 ~ 6 (рис. 4.7). Этого достаточно для вы-
полнения любой работы комплекса.
Полный резерв времени показывает, насколько может быть уве-
личена сумма продолжительности всех работ.
Свободный резерв времени – это максимальное время, на кото-
рое можно отсрочить начало или увеличить продолжительность ра-
боты при условии, что все события наступают в ранние сроки. Как
следует из табл. 4.1 для выполнения всего комплекса работ при уров-
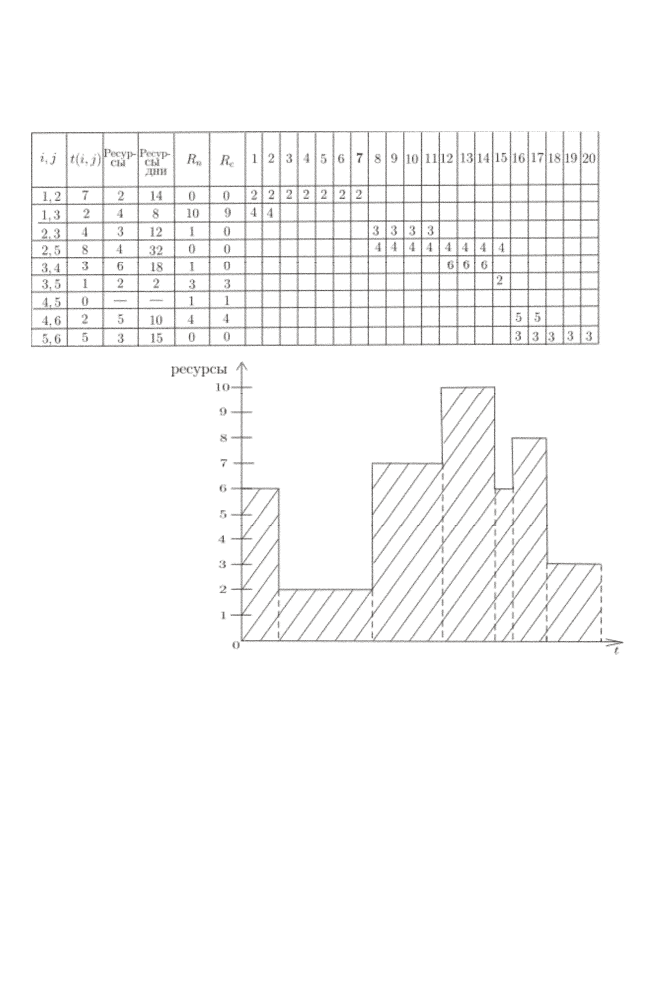
не ресурсов, равном 6, требуется 30 дней, что в полтора раза
превышает срок, определяемый только технологическими условия-
ми. На диаграмме (рис. 4.7) показано ежедневное распределение ре-
сурсов.
Очевидно, что оно крайне неравномерно. Если требуется сокра-
тить длительность выполнения комплекса работ, необходимо увели-
чивать уровень используемых ресурсов. Решение с использованием
семи единиц ресурса дает длительность выполнения комплекса 25
дней (табл. 4.2, рис. 4.8). Для достижения минимально возможной
длительности выполнения, равной 20 дням, потребуется 10 единиц
ресурсов (табл. 4.3, рис. 4.9).
57
Т а б л и ц а 4.1
Р и с. 4.7. Диаграмма распределения ресурсов за 30 дней
Т а б л и ц а 4.2
Р и с. 4.8. Диаграмма распределения ресурсов за 25 дней
58
Рассмотренный при решении примера эвристический метод оп-
тимизации по времени комплекса работ, когда ресурсы ограничены,
не минимизирует время выполнения комплекса работ, но обеспечи-
вает достаточно хорошее приближение к нему.
Т а б л и ц а 4.3
Р и с. 4.9. Диаграмма распределения ресурсов за 20 дней
Возможна и иная постановка задачи: какие дополнительные ре-
сурсы, и в какие работы следует вложить, чтобы общий срок выпол-
нения комплекса не превышал заданный, а стоимость дополнитель-
ных ресурсов минимизировалась.
4.4. Параллельный метод
Исполнитель может выбрать метод ежедневного распределения
ресурсов. Каждый день он решает, какая работа наиболее важная и,
соответственно, распределяет ресурсы. В расчет принимаются только
те операции, которые могут выполняться в текущей день, а также
имеющиеся на этот день ресурсы. Ресурсы распределяются только на

59
один день. На следующий день можно не использовать ресурсы на
прежних работах даже если они не завершены. Они будут завершены
в последующие дни.
Чтобы решить вопрос о важности работ, руководитель ежеднев-
но распределяет приоритеты между ними, исходя из необходимости
завершения всего комплекса работ в кратчайший срок. Кроме того,
он отдает предпочтение уже начатым работам, а также принимает во
внимание количество ресурсов, требующихся для работы. Такая си-
туация анализируется параллельным методом. Правила предпочте-
ния для работ (при условии завершения всех предшествующих им
работ) состоят в следующем:
1) направить ресурсы на выполнение работы, имеющей наи-
меньший резерв времени (при прочих равных условиях);
2) направить ресурсы на выполнение уже начатой работы (при
прочих равных условиях);
3) направить ресурсы на выполнение работы, требующей наи-
большего числа единиц ресурсо-дней (при прочих равных условиях);
4) направить ресурсы на выполнение работы, требующей наи-
большего числа единиц ресурсов на день (при прочих равных усло-
виях);
5) рассмотреть последовательность работ.
В начале и в конце каждого рабочего дня все ресурсы считаются
свободными.
В первый рабочий день приоритет определяется резервом вре-
мени (чем меньше резерв, тем выше приоритет). Распределение ре-
сурсов производится ежедневно и вид распределения может также
изменяться ежедневно. В начале каждого дня, когда происходит рас-
пределение ресурсов, некоторые работы уже закончены, другие за-
кончены частично, остальные ещё не начаты. Приведенные выше
правила предпочтения используются для распределения ресурсов
между работами, находящимися в стадии выполнения, а также теми,
которые могут быть начаты.
ЛЕКЦИЯ 7
4.5. Учет стоимостных факторов
при реализации сетевого графика
Стоимостные факторы при реализации сетевого графика учиты-
ваются путем определения зависимости «затраты – продолжитель-
