Лубенцова В.С. Математические модели и методы в логистике
Подождите немного. Документ загружается.

30
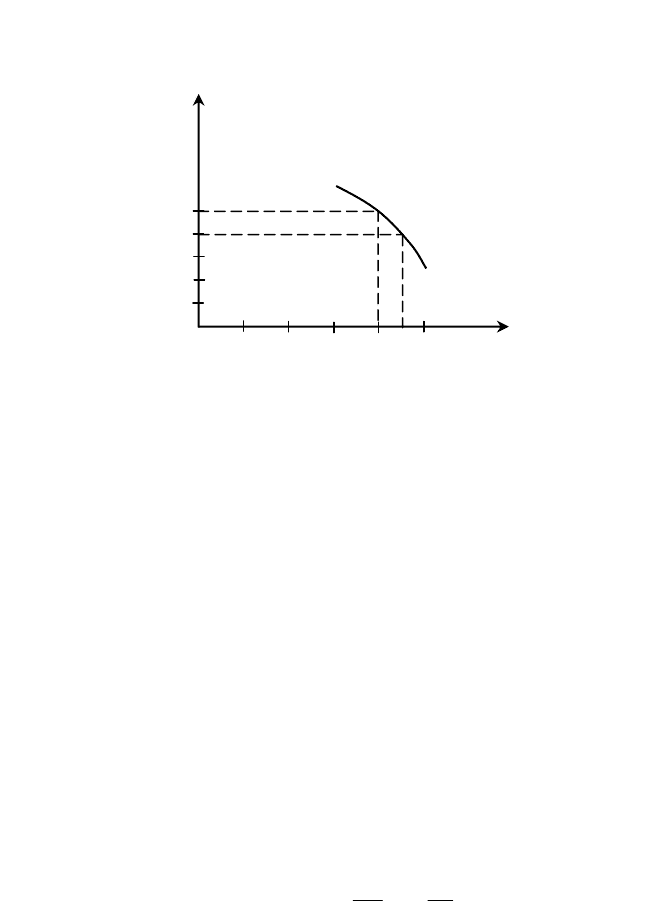
На основании этих данных построим зависимость Об=f(K)
(рис. 2.2).
С помощью графика (рис. 2.2) можно решать два вида задач.
1. По заданному качеству продукции К выявить возможный объ-
ём её выпуска Об.
2. По заданному объёму определить возможное качество К. Та-
ким образом, за качество продукции надо платить уменьшением объ-
ёмов её выпуска. В связи с этим задача максимизации объема Об при
максимизации качества К не может быть выполнена. Возможно най-
ти лишь компромиссное решение.
Эта задача в общем виде записывается следующим образом:
1
зад
1
1
Об max,
,
,
,1,,1,;
n
jj
j
n
jj
j
n
ijji
j
jjj
cx
KsxK
axb
dxDimjn
=
=
=
=→
=≥
≤
≤≤==
∑
∑
∑
0
Об
K
1300
1200
1100
1000
900
600 700
800
900 1000
Р и с. 2.2. График зависимости объема
от качества

31
1
зад
1
1
max,
ОбОб ,
,
,1,,1,.
n
jj
j
n
jj
j
n
ijji
j
jjj
Ksx
sx
axb
dxDimjn
=
=
=
=→
=≥
≤
≤≤==
∑
∑
∑
В результате решения должны быть получены зависимости:
в первом случае
(
)
зад
Об fK= , во втором –
(
)
Об
Kf= .
Таким образом, применяя метод последовательных уступок,
сложно установить зависимость объёма выпуска продукции от каче-
ства и на основании этой зависимости выбирать связанные между
собой оптимальные значения параметров Об и К. Следовательно,
реализовать оптимальное решение можно лишь при строгом соблю-
дении зависимости между этими параметрами. А такой зависимо-
стью является получаемая в результате применения метода последо-
вательных уступок графическая зависимость, представленная на
рис. 2.2. Не вызывает сомнения, что этот метод можно обобщить на
случай большого числа параметров. Если стоит задача максимизации
по к параметрам, то один из них следует принять в качестве целевой
функции, а в остальные ввести ограничения.
ЛЕКЦИЯ 4
2.3. Метод экспертных оценок.
Непосредственное назначение коэффициентов веса
Этот метод основан на построении единого (интегрального) по-
казателя эффективности посредством суммирования произведения
имеющихся показателей на соответствующие весовые коэффициенты
(коэффициенты важности показателей).
Одним из распространенных методов определения степени от-
носительной важности является назначение коэффициентов веса, ко-
торые, как правило, находят с помощью методов экспертных оценок.
Назначение коэффициентов веса с помощью экспертизы представля-
ет собой, по существу, обычное обсуждение, с той лишь разницей,
что свое мнение эксперты выражают не словами, а цифрами. Методы
32
экспертных оценок достаточно широко распространены в спорте,
например, в фигурном катании, гимнастике. Нет основания считать
неприемлемым коллективное мнение специалистов при принятии
оптимальных решений. Методов определения экспертных оценок
достаточно много. Рассмотрим метод непосредственного назначение
коэффициентов веса. Согласно этого метода каждый i-тый эксперт
для каждого к-того параметра должен назначать коэффициент
ik
α
таким образом, чтобы сумма всех коэффициентов веса, назначенных
одним экспертом для различных параметров, равнялась единице:
1
1,1,
n
ik
k
in
α
=
==
∑
,
где
n
– число экспертов.
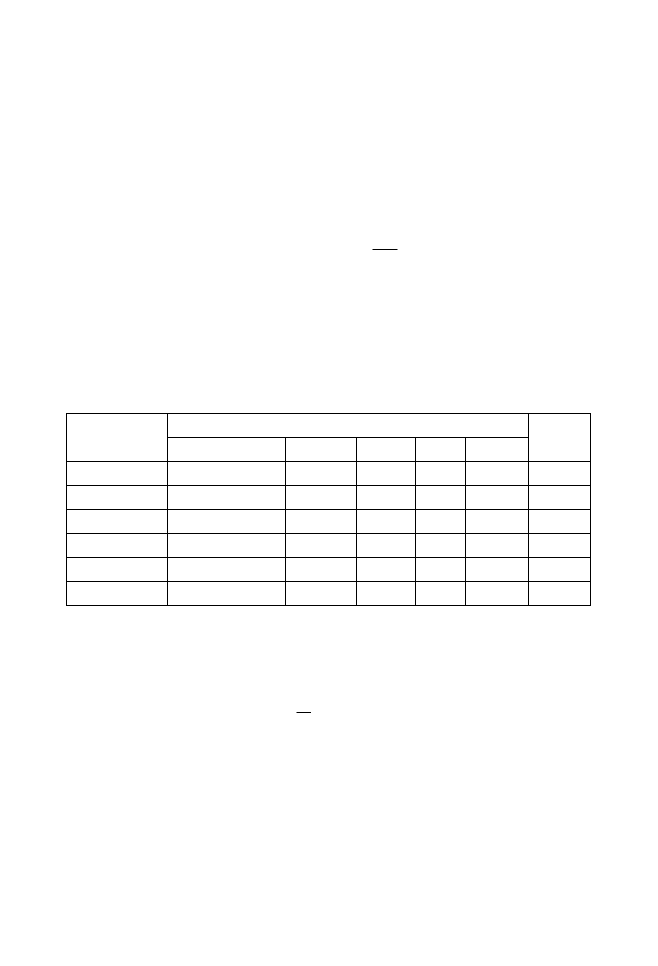
Результаты экспертизы сводятся в табл.2.6.
Т а б л и ц а 2.6
Параметры
Эксперт
1 … k … K
∑
1 a
11
a
1k
a
1K
1
…
i a
i1
a
ik
a
iK
1
…
n a
n1
a
nk
a
nK
1
α
k
a
1
a
k
a
K
В качестве коэффициента веса к-го параметра принимают сред-
нее значение по результатам экспертизы всех экспертов:
1
1
1
n
kik
i
n
αα
=
==
∑
.
Например, нас интересует сравнительная важность двух пара-
метров: объёма выпуска продукции и её качества. Пусть для экспер-
тизы пригласили 8 человек. Результат экспертизы приведён
в табл. 2.7.
Здесь значения экспертных оценок
1
0,75
α
=
,
2
0,25
α
=
.
Если
3
k
≥
, то, как показывает опыт, удовлетворение требования
1
1
n
k
k
α
=
=
∑
затруднено. Для того чтобы избежать выполнения этого
требования, можно определить коэффициенты другими методами.
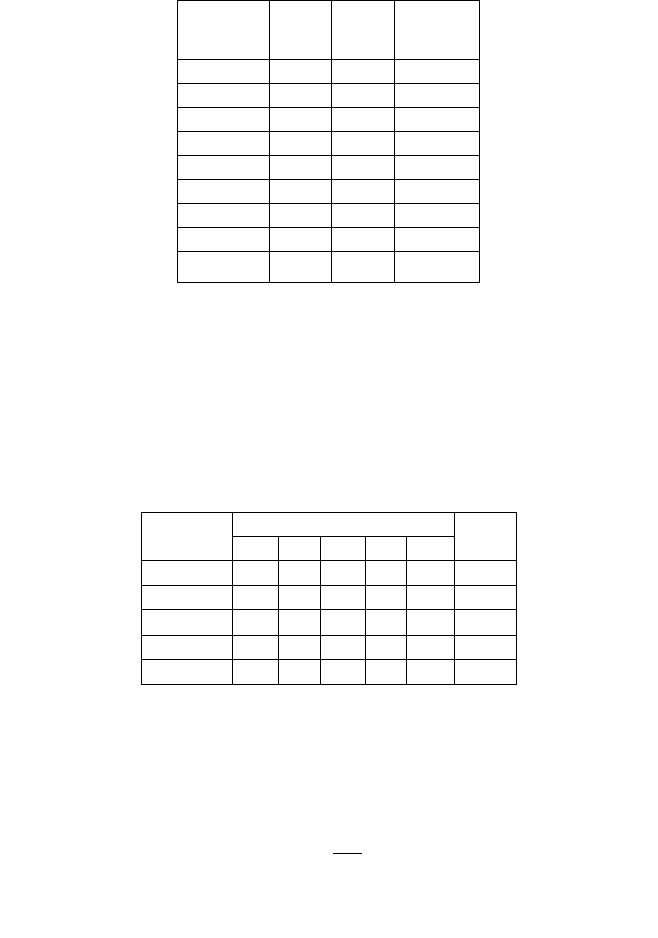
33
Т а б л и ц а 2.7
Эксперт Об К
1
n
k
k
α
=
∑
1 0,8 0,2 1
2 0,9 0,1 1
3 0,7 0,3 1
4 0,7 0,3 1
5 0,6 0,4 1
6 0,8 0,2 1
7 0,7 0,3 1
8 0,8 0,2 1
k
a
0,75 0,25 1
2.4. Оценки точности параметров в баллах
В этом случае каждый i-тый эксперт назначает каждому к-му
параметру оценку по десятибалльной системе. Наиболее важный па-
раметр оценивают более высоким баллом, при этом различным па-
раметрам может быть назначен одинаковый балл. В результате экс-
пертизы заполняется табл. 2.8.
Т а б л и ц а 2.8
Параметры
Эксперт
1 … k … K
∑
1
β
11
β
1k
β
1K
β
1
…
i
β
i1
β
ik
β
iK
β
i
…
n
β
n1
β
nk
β
nK
β
n
Для каждого эксперта определяется сумма:
1
n
iki
k
ββ
=
=
∑
и находятся значения коэффициентов веса:
ik
ik
i
β
α
β
= .
Эти данные представляют строку для i-того эксперта; аналогично
определяются значения весовых коэффициентов для остальных экс-
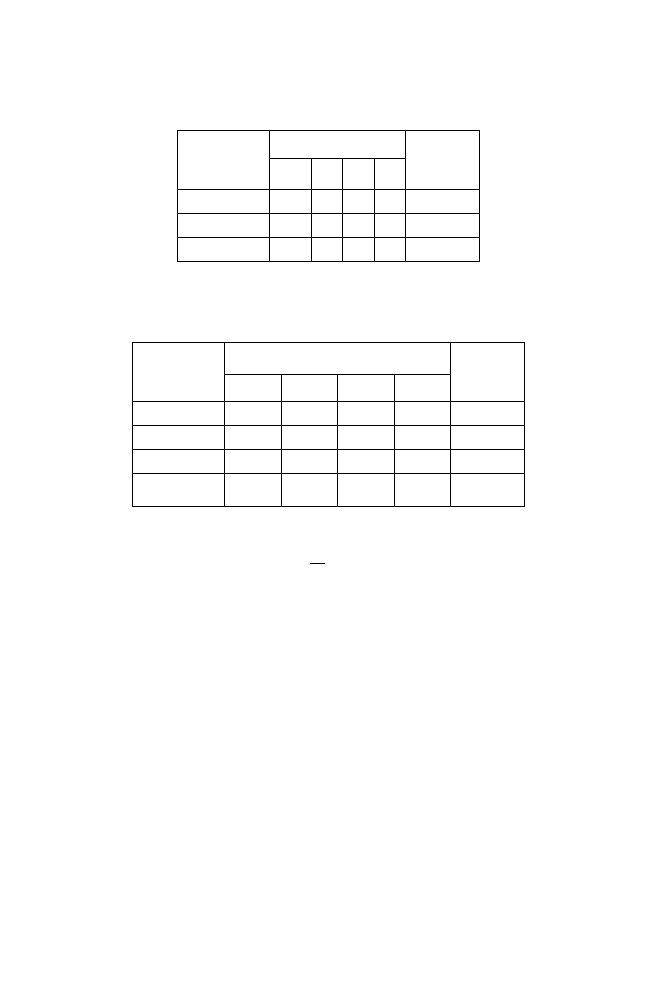
34
пертов.
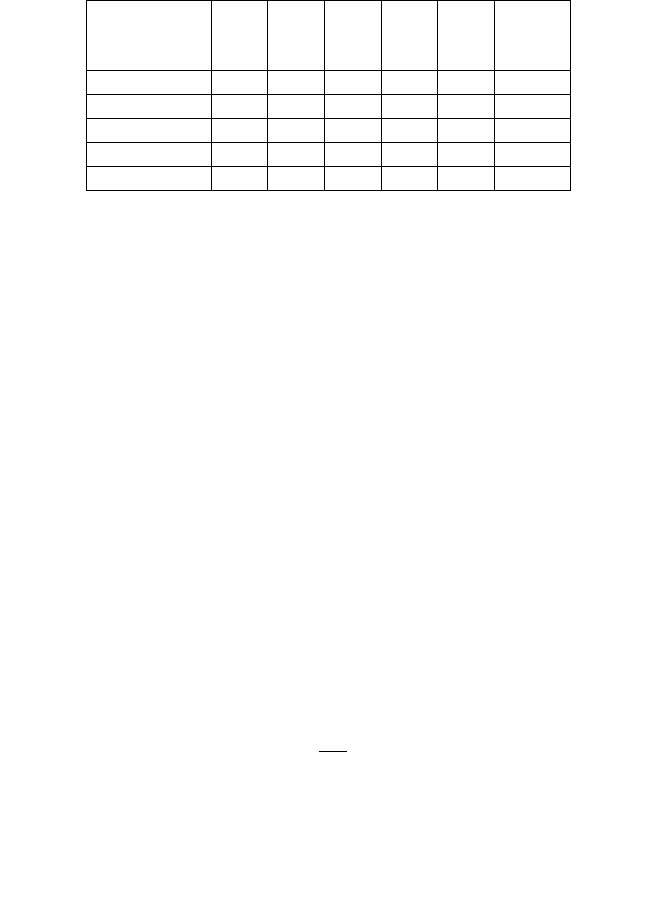
Здесь данные экспертизы оформляются в виде табл. 2.9 и 2.10.
Т а б л и ц а 2.9
Параметр
Эксперт
1 2 3 4
1
n
k
k
β
=
∑
1 6 5 9 7 27
2 10 8 4 9 31
3 5 8 9 3 25
Т а б л и ц а 2.10
Параметр
Эксперт
1 2 3 4
1
n
k
k
α
=
∑
1 0,22 0,19 0,33 0,26 1
2 0,32 0,25 0,13 0,3 1
3 0,2 0,32 0,36 0,12 1
k
а
0,25 0,25 0,27 0,23 1
1
1
n
kik
k
n
αα
=
=
∑
.
2.5. Статистический метод экспертных оценок
В результате опроса экспертов принимают среднее значение
экспертных оценок. Такой подход не учитывает разброса оценок, да-
ваемых каждым экспертом в отдельности, а разброс является показа-
телем того, что-либо вопрос поставлен недостаточно однозначно,
либо признаком некомпетентности экспертов, либо следствием и то-
го и другого. Вместе с тем, неучёт разброса экспертных оценок мо-
жет привести к неправильным выводам.
Для исключения этого недостатка необходимо исходить из того,
что оценка, данная отдельным экспертом, представляет собой реали-
зацию случайной величины и поэтому обработка результатов экспер-
тизы должна производиться по правилам действий со случайными
величинами. Проведение экспертизы рассматривается на примере
определения коэффициентов веса
i
α
параметров
i
x
. Определение
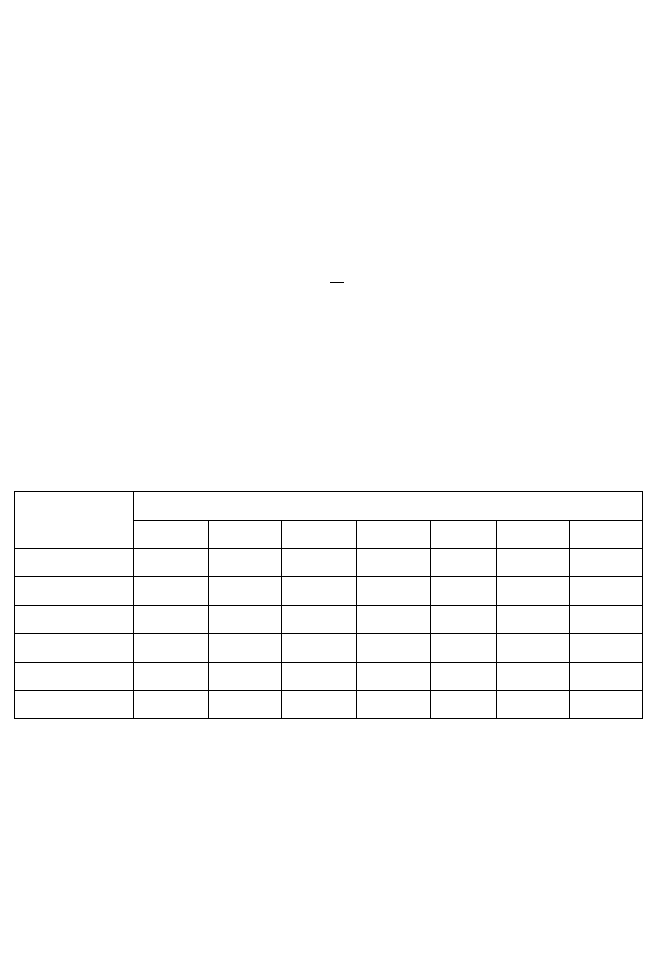
35
экспертных оценок ведётся следующим образом:
1) каждый эксперт должен независимо от других выразить коли-
чественно важность параметров
12
,,...,
k
xxx
, придав коэффициентам
веса
12
,,...,
k
ααα
соответствующие положительные значения таким
образом, чтобы
1
1
n
ik
k
α
=
=
∑
,
i
– число экспертов, к – число параметров;
2) приведенные результаты эксперимента свести в таблицу;
3) по результатам произведённой экспертизы для каждого коэф-
фициента веса найти оценку математического ожидания:
[ ]
1
1
n
kik
i
Md
n
α
=
=
∑
,
затем определить отклонение в оценке каждого эксперта от оценки
математического ожидания:
[
]
ikikik
M
αα
∆=−
и составить новую табл. 2.11;
Т а б л и ц а 2.11
Параметры
Эксперт
α
i1
∆
i1
α
i2
∆
i2
…
α
ik
∆
ik
1
α
11
∆
11
α
12
∆
12
α
1k
∆
1k
2
α
21
∆
21
α
22
∆
22
α
2k
∆
2k
…
i
α
i1
∆
i1
α
i2
∆
i2
…
α
ik
∆
ik
…
n
α
n1
∆
n1
α
n2
∆
n2
…
α
nk
∆
nk
4) обсудить результаты проведенной экспертизы, предоставить
слово для обоснования своей оценки в первую очередь тем экспер-
там, у которых отклонения наибольшие; с помощью вопросов и об-
щей дискуссии добиться устранения возможного недопонимания то-
го, что имеется в виду под оцениваемыми параметрами;
5) провести повторную экспертизу, результаты которой свести в
таблицу экспертных оценок, но без столбцов со значением ∆
ik
; затем
по данным таблицы определяются оценки математического ожида-
ния и оценки дисперсий:
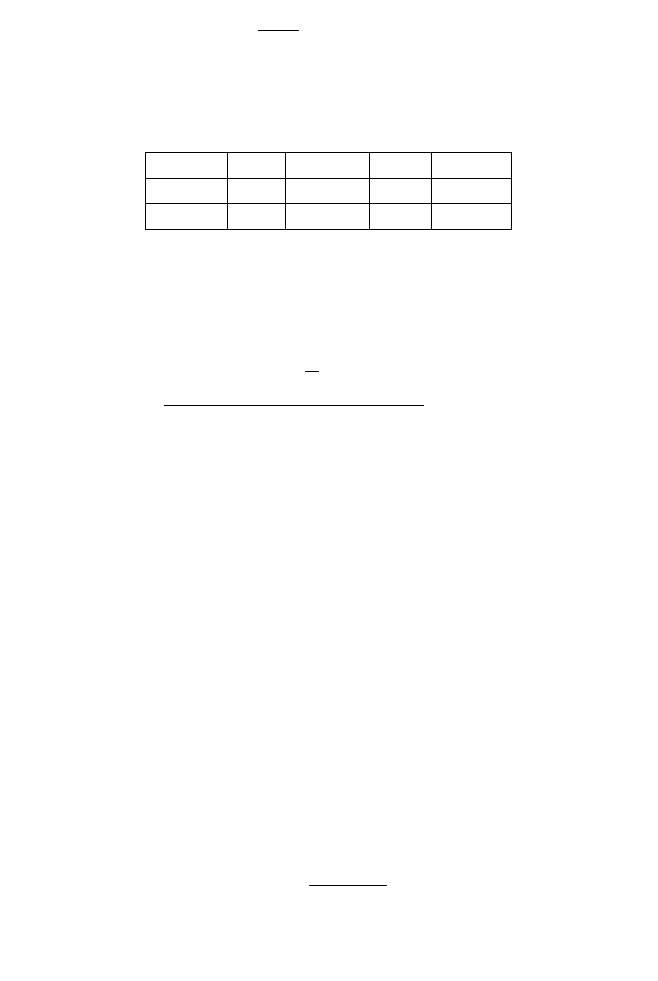
36
[ ]
[ ]
( )
2
1
1
1
n
kikik
i
DM
n
ααα
=
=−
−
∑
,
которые сводятся в табл. 2.12:
Т а б л и ц а 2.12
α
1
…
α
k
…
α
K
M[α
1
]
…
M[α
k
]
…
M[α
K
]
D[α
1
]
…
D[α
k
]
…
D[α
K
]
При обработке окончательных результатов экспертизы для ха-
рактеристики степени согласия мнения исследователей о ранжировке
коэффициентов веса вычисляют коэффициент конкордации:
( )
( )
2
11
23
1
121
2
kn
ik
jj
kk
W
nkk
α
==
−+
=
−
∑∑
,
01
W
≤≤
,
k
– число рассматриваемых параметров,
n
– число экспертов.
2.6. Метод бинарных (парных) соотношений
Если совместная оценка всех параметров вызывает затруднения,
их можно сравнивать попарно, т.е. методом попарных соотношений.
Например, пусть задано 5 параметров
1
x
,
2
x
,
3
x
,
4
x
,
5
x
. Каждый i-
тый эксперт назначает парные соотношения:
1,
если тый параметр важнее того,
0, в противном случае
kj
kj
γ
−−
=
и для i- того эксперта составляется табл. 2.13, причем
55
11
10
kj
jk
γ
==
=
∑∑
.
Определяем экспертную оценку
5
1
55
11
kj
k
k
kj
kj
γ
α
γ
=
==
=
∑
∑∑
для i-того эксперта. В результате получим
1
0,3
α
=
;
2
0,2
α
=
;
3
0
α
=
;
37
4
0,3
α
=
;
5
0,3
α
=
.
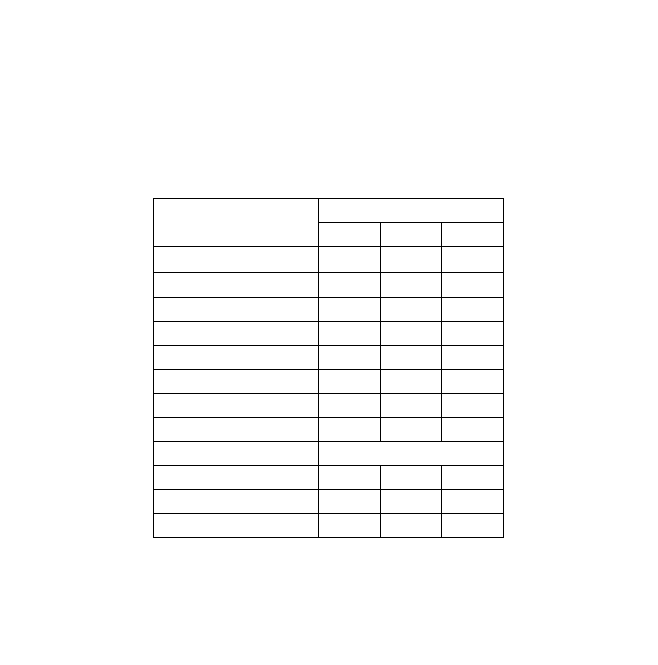
Т а б л и ц а 2.13
Сравни-
ваемые
параметры
x
1
x
2
x
3
x
4
x
5
5
1
kj
j
r
=
∑
x
1
— 0 1 1 1 3
x
2
1 — 1 0 0 2
x
3
0 0 — 0 0 0
x
4
0 1 0 — 1 3
x
5
0 1 1 0 — 2
Из последней строки нижней таблицы видно, что, несмотря на
отсутствие, казалось бы, какой-либо закономерности в оценках, дан-
ных экспертами, все параметры имеют примерно одинаковую отно-
сительную важность.
Приведенные методы определения коэффициентов веса дают
возможность получить достаточно достоверные исходные данные,
позволяющие оценить важность каждого оптимизируемого парамет-
ра.
2.7. Пример решения задачи методом экспертных оценок
Вернёмся к задаче многопараметрической оптимизации, которая
представляет собой попытку найти некоторый компромисс между
теми параметрами (целевые функции), по которым требуется опти-
мизировать решение. Возможной реализацией такого компромиссно-
го подхода является формирование специальной функции. При этом
компромиссная целевая функция должна удовлетворять следующим
требованиям: оптимизируемые параметры (целевые функции),
имеющие, как правило, различную размерность, должны быть при-
ведены к безразмерной форме, максимизируемые параметры входят
со знаком плюс, минимизируемые – минус:
1
max
K
k
k
k
kn
x
F
x
α
=
=→
∑
.
В этой целевой функции оптимизацию производят по
K
пара-
метрам. Безразмерность параметров обеспечиваем введением норми-
рующей величины
kn
x
, а степень компромисса назначается с помо-
щью коэффициентов
k
α
.

38
Нормирующая величина может задаваться различными спосо-
бами. В одном случае значение нормирующей величины
kn
x
прини-
мается из какого-нибудь утверждающего документа, например, тех-
нического задания. Если такой утвержденной величины нет, то мож-
но решить задачу оптимизации при максимизации этой величины,
т.е.
max
FF
=
, и полученное в результате оптимизации значение
*
k
F
принять за нормирующее:
*
кн
k
FF
= . Коэффициенты веса назначаются
при условии
1
1
n
k
k
α
=
=
∑
с помощью экспертных оценок.
Для рассмотренного выше примера целевая функция записыва-
ется следующим образом:
12
нн
Об
max
Об
K
F
K
αα=+→.
В качестве нормирующих значений
н
Об
и
н
K
принимаем их
максимальные значения, полученные в результате оптимизации от-
дельно по каждому параметру:
н
Об 1340
=
,
н
1028
K
=
. Математиче-
ская модель задачи имеет вид:
12
Об
max
13401028
K
F αα=+→;
123
123
123
123
123
1
Об 71213;
9710;
0,20,30,435;
0,50,40,342;
0,60,81,2100;
0,1,3.
xxx
Kxxx
xxx
xxx
xxx
xj
=++
=++
++≤
++≤
++≤
≥=
Результаты решения этой задачи при различных значениях ко-
эффициентов веса
1
α
и
2
α
приведены в табл. 2.14.
Анализ табличных данных даёт основание сделать нижесле-
дующие выводы.
1. С точки зрения объёма выпускаемой продукции наиболее вы-
годным является 1 вариант. По мере снижения коэффициента веса
1
α
её выпуск уменьшается. Самой невыгодной является продукция П1,
которая при
1
α
вообще не производится.
39
2. Наиболее выгодной с позиции качества является продукция
ПЗ. Наиболее невыгодной – П2, которая при
2
1
α
=
не выпускается.
3. Для обеспечения дальнейшего роста объёма выпуска продук-
ции необходимо увеличить трудовые и материальные ресурсы, а для
повышения качества продукции – материальные и финансовые.
Т а б л и ц а 2.14
Варианты
Характеристики
1 2 3
α
1
1 0,5 0
α
2
0 0,5 1
F 100 94,4 100
Об(F
1
) 1340 1260 1108
К(F
2
) 830 930 1028
П1(X
1
) 0 20 49
П2(X
2
) 90 50 0
П3(X
3
) 20 40 59
Резерв ресурсов:
трудовых 0 0 1,7
материальных 0 0 0
финансовых 4 0 0
Данные расчёты показывают, как влияют назначенные коэффи-
циенты веса на результат. Таким образом, зная желаемый компро-
мисс, следует принять коэффициенты веса, которые определяют по-
лученное решение.
