Leray J. Lagrangian Analysis and Quantum Mechanics: A Mathematical Structure Related to Asymptotic Expansions and the Maslov Index

Подождите немного. Документ загружается.

234 11 1,§4,1-111,§4,

Lo=h(l+2Mo=hm,

cL LO

-4vz,

that is, by (2.3) of §3,

aL:-CL

v2Ap-h2[l+2

2vh][1+2+2vh]

= -h2[Ao + l(l + 1)] for v = i/h,

1 8

Q-CM=

(

-X2-

- hm.

Assume that K is a holomorphic function of R at the origin. Let

Co = -K[0, hm],

y = .%(l +

21)2

+ Coh-2.

(1.6)

Apply Fuchs's theorem, that is, the theory of regular points of analytic

ordinary differential equations: see, for instance, [19], section 10.3.

Fuchs's theorem constructs two independent solutions of equation (1.3).

If 27 is not an integer, the respective quotients of these solutions with

R±Y+I/2 are holomorphic at the origin. If y is purely imaginary, then

every nonzero solution of (1.3) makes the integrals (1.4) diverge at the

origin. The same is true if y = 0 (see Fuchs). Assume y > 0. The solution

v of (1.3) that is a product of Ry4

2 and

a holomorphic function at the

origin makes the integrals (1.4) converge at the origin, while the other

solutions of (1.3) make them diverge (see Fuchs). Thus, since problem

(1.3) is equivalent to problem (0.1), the following theorem holds.

THEOREM 1.2.

If K is holomorphic at the origin, then problem (0.1) is

solvable if and only if the following problem is solvable: To find two integers

l and m such that

Iml <l,

y>0,

and such that the nonzero solution v of (1.3), whose quotient with Rl+1r2 is

holomorphic at the origin, satisfies

v2dR < oo,

()2dR

< oc.

(1.7)

2. The Schrodinger-Klein-Gordon Case

In this case, that is, under assumption (0.4), the preceding theorem can

be supplemented. Let

III,§4,2

235

MO = hm,

AO = A(M0),

Bo = B(M0),

Co = C(M0),

a = Aoh-1,

= Boh-z.

Equation (1.3) becomes the confluent hypergeometric equation:

d 2V

dR2 +

[

yZ R1/41z

where a2, fl, and y e R, y > 0. If a2 > 0, then choose a > 0.

Let v be the nonzero solution of (2.2) such that

vR-Y-112 is

an entire

function of R ; it is defined up to a multiplicative constant (Fuchs).

LEMMA 2. The convergence of the integrals (1.7) is equivalent to the

following condition:

+ 2 - }' is a positive integer.

(2.3)

Proof.

Express v by

v(R) = RY+1/2e-aR E CsR',

cs E C.

(2.4)

seN

Substituting into (2.2), we obtain (Fuchs) the recurrence formula defining

the cs in terms of co :

s(s + 2y)c5 = 2[a(s + y - z)

- fl]c_1

Condition (2.3) holds if and only if

E c5Rs is a polynomial.

It implies a2 > 0; thus a > 0 and thus the integrals (1.7) converge.

Now let us prove that (1.7) does not hold when (2.3) is not satisfied.

Case when a > 0:

If EScSR' is not a polynomial, then, for an ap-

propriate choice of the sign of co,

cs > 0 for s near + oc.

Let E E 10, a[. From (2.5) we have

scs > 2ec5_ 1 for s near + oe ;

thus ESc,R' > c'e2,1 for R near + oc, where c' = const. > 0,

and the integral (1.7)1 diverges.

236

III,§4,2

Case when az < 0:

The classical integral expression for v gives an

asymptotic expression for v which is also classical: for R near + oc,

v(R) = ceaRR-Pla + ce-aRRP1a + .

where c and care constants and a is purely imaginary. Hence the integral

(1.7)1 diverges. (See Whittaker and Watson, [19], chapter XVI, "The Con-

fluent Hypergeometric Function: Asymptotic Expansion.")

Case

when a

= 0, f < 0: By (2.5),

v(R) = Ry' 1/2

c,R5, where cs > 0

Vs;

sEN

thus the integral (1.7)1 diverges.

Case when a = 0, $ > 0: R-r-'/zV satisfies a differential equation

with linear coefficients. Laplace's expression for its solution gives

v(R) _ k I

t-2y-'e`2 R(-t-')dt

v JT

where T is the boundary of a half-strip in C containing the cut I - oo, 0[.

By replacing T by a path on which Re(t - t-') -< 0 (=0 only for t = i)

and assuming that R is near + oo, we obtain the asymptotic value

v(R) =

R+ ce-2i,/2%1R] + ...

Thus integral (1.7)1 diverges.

Theorem 1.2 and lemma 2, where a and $ are defined by (2.1) and y

by (1.6), prove the following.

THEOREM 2. When a is the Schrodinger-Klein-Gordon operator, then, for

each of the following problems, namely,

1°) the classical problem (0.1) that we have just reviewed,

2°) the lagrangian problem (2.1) in §3,

aU = (aL: - cL)U = (am - cM)U = 0 on compact V,

3°) the same problem mod(1 jv2), that is, problem (3.1) in 41,

the condition that there exist a solution is the same: the existence of a

triple of integers (l, m, n) satisfying condition (4.11) of §1, theorem 4.

Remark 2.

A comparison of theorem 1.2 and theorem 3.1, 1°) of §1

III,§4,2-1I I,§4,Conclusion

237

proves that the preceding theorem does not hold for every operator a

associated to a hamiltonian H of the form (0.2).

Conclusion

Although the classical boundary-value problems and the lagrangian prob-

lems are completely independent, they define the same energy levels for the

Schrodinger and Klein-Gordon equations.

As a matter of fact the experimental values of the energy levels agree

with those of the Dirac equation, which is studied in the following chapter.

Dirac Equation with the Zeeman Effect

Introduction

In §1, we solve, mod(1/v2), a homogeneous lagrangian problem in several

unknowns. That is one of the simplest problems to which theorem 3 of

II,§4 can be applied. The resolution of this problem introduces the qua-

druple of quantum numbers that arises in the study of the Dirac equation.

In §2, we use lagrangian analysis to reduce the Dirac equation mod(1/v2)

to the simpler system solved in §1. This reduction is analogous to the

reduction theorem 2.2 of II,§4. Thus we prove that the lagrangian solutions

of the Dirac equation (one-electron atoms in a magnetic field) defined

mod(l/v2) on compact manifolds have energy levels that are exactly those

for which the classical solution of this equation exists (taking into account

the Zeeman effect and even the Paschen-Back effect).

§1. A Lagrangian Problem in Two Unknowns

In this §1, we give an application of II,§4,theorem 3.

1. Choice of Operators Commuting mod(1/v3)

As in III,§1,1, we let

X = X* = E3,

x,pcE3,

R(x) = Ix P(p) _ Cpl,

Q(x, p) = <p, x>,

L(x, p) = Ix A Ph

so that

L2 + Q2 = P2R2.

(1.2)

Let (M1, M2, M3 = M) be the components of x A p.

By III,§l,(1.3), the following formulas define three functions H"1, H«

and H13j that are pairwise in involution (see [1I,§l,2):

H")(x,

p) = H[L(x, p), M(x, p), Q(x, p), R(x)],

(1.3)

P) = L2 (x, p),

H13 (x,

P) = M(x, P)

To use theorem 3 of I1,§4, we must choose three it x it matrices

j121,

and J(3) that are functions of (x, p) c E3 O+ W. These must be such that

the matrices of lagrangian operators associated to the three matrices

H'k)E +

J'k)

(E the p x p identity matrix)

(1.4)

IV,§ 1,1

239

commute mod (1 /0).

Since the H(k) are in involution, it follows by remark 3 of II,§4 that this

commutivity condition is equivalent to the condition that for all i, k,

(H(h J(k)) - (H(k) J( )) + J(n J(k)

j(k) j(i) = 0,

(1.5)j

where (,

) is the Poisson bracket.

We choose p = 2. Then the values of the J(k) are matrices acting on

vectors in the space C2, which we provide with a hermitian structure.

We choose the iJ(k" to be self-adjoint. (The vectors in C2 are called spinors.)

Notation.

Let ao = 1 be the 2 x 2 identity matrix. Every 2 x 2 self-

adjoint matrix has the form x0c0 + or, where xo is a real number and a

is a self-adjoint matrix with zero trace:

Q = Q[x1, X2, x3]

x 3

x1 - ix2

x1 + 1x2 -x3

where

(x1, x2, x3) e E3

and

= x1Q1 + x262 + x363,

(1.6)

Q1 =

(01

10),

62 =

00,

-- )

Q3 = (0

are the Pauli matrices, which satisfy the relations

Qk = 1,

Cork = -ak(ri, Q1Q2Q3 = i.

(1.7)

It follows that

Q2[x] _ N2.

(1.8)

Remark 1.1.

Recall the consequences of (1.8): Let u2 be a measure-

preserving automorphism of C2, that is, u2 E SU(2); u2Q[x]u2 1

is self-

adjoint and has zero trace; thus it is of the form a[y]. Let y = ux. Then

Q[ux] = u2Q[x]uj

By (1.8), u preserves Ixl2. More precisely, u is a rotation in E3, that is,

u E SO(3), whence we obtain a morphism

SU(2) 3 a2 H u e SO(3),

240

IV,§1,1-IV,§1,2

which proves that SU(2) is the covering group of SO(3) of order 2. It is

the universal covering group of SO(3) (see Steenrod [17], p. 115).

LEMMA 1.

Assume

J(1j = if a3 + iga[x A p],

is a datum, where

f(x, p) = f [L(x, p), M(x, p), Q(x, p), R(x)],

g = g[L, M, Q, R].

Then (1.5) is satisfied by choosing

J(2) = 0,

- 2Q3.

(1.10)

Remark 1.2.

Relations (1.5) evidently remain valid when arbitrary com-

plex numbers (that is, their products with the identity matrix denoted

by co = 1) are added to the H)`) and P'`).

Proof of (1.5)1.2.

(H12!, J(1)) = 0 because, by III,§1,1, L is in involution

with Q, R, and M = M3, and similarly with M1 and M2.

Proof of (1.5)1,3.

Since M is in involution with L, Q, and R,

(H)3), J(1))

= ig(M,

a[x A P]) = iga[-M2, M1, 0] (1.11)

because an immediate and classical calculation gives

(M. M1) = -M2,

(M, M2) = M1.

Moreover, (1.7) implies

a3a[x A p] - o[x A p]a3 = 2icr[-M2, M1, 0];

whence, by the definitions (1.9) and (1.10) of Jj1) and J(3),

J(3)J(l)

j(l)j(3)

_ -iga[-M2, Ml, 0];

(1.12)

(1.5)1,3 results from (1.11) and (1.12).

The proof of (1.5)2,3 is evident.

2. Resolution of a Lagrangian Problem in Two Unknowns

Notation.

Let

af.s'

aL2,

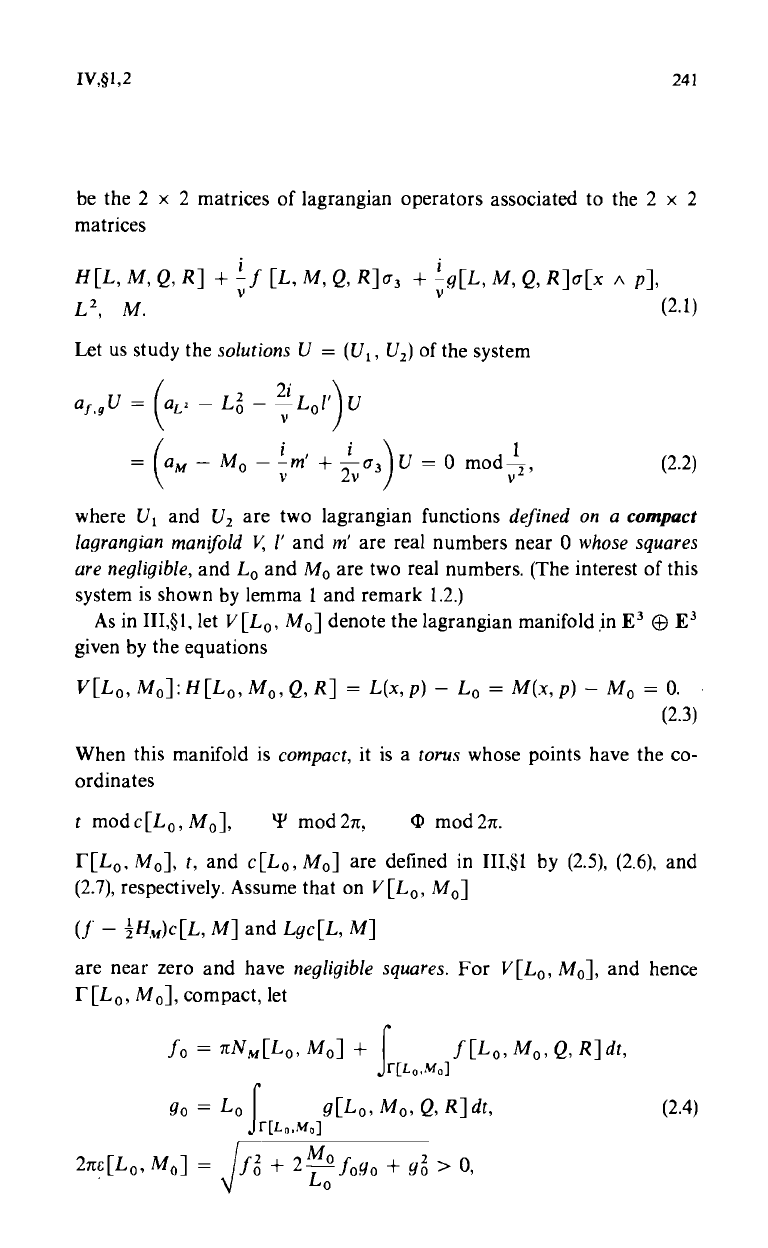
IV,§1,2

241

be the 2 x 2 matrices of lagrangian operators associated to the 2 x 2

matrices

H[L, M, Q, R] + v f [L, M, Q, R]a3 +'g[L, M, Q, R]a[x A P],

L2, M. (2.1)

Let us study the solutions U = (U1, U2) of the system

at,gU = (aLl - Lo -

2i Lol')

(a,M

- Mo -

'm'+ 2v a3)

U = 0 mod

z ,

where Ul and U2 are two lagrangian functions defined on a compact

lagrangian manifold V,

l' and m' are real numbers near 0 whose squares

are negligible, and Lo and Mo are two real numbers. (The interest of this

system is shown by lemma 1 and remark 1.2.)

As in 111,§ 1, let V [Lo, Mo] denote the lagrangian manifold in E3 Q E3

given by the equations

V [Lo, Mo] : H [Lo, Mo, Q, R] = L(x, P) - Lo = M(x, P) - Mo = 0.

(2.3)

When this manifold is compact, it is a torus whose points have the co-

ordinates

t modc[L0,M0],

'P mod 27r, (D mod 27r.

F[Lo, Mo], t, and c[Lo, Mo] are defined in III,§1 by (2.5), (2.6), and

(2.7), respectively. Assume that on V [Lo, Mo]

(f - ZHN)c[L, M] and Lgc[L, M]

are near zero and have negligible squares. For V[L0, Mo], and hence

I'[L0, M0], compact, let

.fo =7<NM[Lo,Mo] +

.f[Lo,Mo,Q,R]dt,

Jr[L0,M0]

go = Lo

g[Lo, Mo, Q, R] dt,

(2.4)

r[L,,M0]

27re[L0, Mo]

= fo + 2

o.fogo + go > 0,

242 IV,§1,2

where IMOI < L0. We shall see that f0, g0i and c have negligible squares.

THEOREM 2.

The compact manifolds V in E3 Q+ E3 on which solutions U

of the system (2.2) are defined are the tori V [L0, M0] such that

Lo=h(l+i-I'), M0=h(m-rn'),

(2.5)

h(l +

i) +

N [h(1

+ 4), hm] = fin

± hs[h(1 + ' ), hm],

where 1, m - i, and n are three integers satisfying the inequalities

Iml

l+z, 1<n;

(2.6)

V and m' are numbers near 0 that are arbitrary unless m = I + '-z. Then

they must be chosen so that

IM01 < L0.

Remark 2.1.

U will be denoted by U+ or U_ depending on whether

(2.5)3 holds with the choice + or -. The lagrangian amplitude

A, f2) of U = U+ will be denoted by /3± . It satisfies the relations

/3±(t + c[L0, M0], `E, (D) =

c±i #+(t,'p, (D),

lf+(t, `Y + Zit, (D) = c±2 f3±(t, IF, (D),

(2.8)

fl±(t,'I','D + 2n) = c±3 f3± (t, Y', (D)

The

are complex numbers with modulus 1 given by

Cfi = e 2rzi(l'NL[Lu.Mo]+m'N.d[Lo,Mo]+e[Lo,Mo])

' '

2.9)

2nim

C+2 =

e2nil

±3 = -e

Proof.

By lemma I and remark 1.2, theorem 3 of l1,fi4 can be applied.

Then the V on which a solution U of the system (2.2) is defined are the

covering spaces of the manifolds V given by the equations (2.3). The

compact V are the tori V [L0, M0]. Let us determine when U is defined

on V [L0, M0], that is, when

(j)'2e0ofl:

V [L0, M0] -' C2,

(2.10)

where R0 is the frame we are using,

arg rl = 0,

arg d 3x = mR,,

and mRo and rpR are the Maslov index and the phase of V[L0, M0] in R0.

IV,§1,2 243

By (3.5) and (3.4) of IIL§1,

mRo =

1In

- I arctan

HR1,

where [ ] = integer part,

(2.11)

PRO=S2+LO'P+M0D,

where 0 is defined in III,§1 by (2.8).

We now finish applying theorem 3 of II,§4. By the remarks 3.2 and

3.3 of III,§1, the characteristic vectors K, KL2, and KM of the hamiltonians

H, L Z, and M are

K:dt = 1, d'P = HL,

d(D = Hy;

KL':dt=0,

d`P =2L0, dD=0;

KM:dt=0, d'!=0, dl = 1.

Then by this theorem the system (2.2) is equivalent to the condition

;

' aT

Mad

Q + ifQ0 + igQ[x n P]I3 = 0,

- il'/3 = 0,

- -

im'/3 +

r3 f l = 0.

cq)

In other words, it is equivalent to the pfaffian system

df1 + i{ fa3dt + gx[x A p]dt - l'(dT - HLdt)

- (m' - za3)(d(D - HM dt)}Q = 0,

(2.12)

which is guaranteed to be completely integrable by this theorem. By (1.5)

of III,§1,

x A p = LOJ3;

thus by (1.12)3 and (1.11) of III,§1,

(r[X A p] = L [Q, cos 4) sine + Q2 sin 0 sine + Q3 cos O],

where

cos o =

(2.13)

Then, by (1.7),