Leray J. Lagrangian Analysis and Quantum Mechanics: A Mathematical Structure Related to Asymptotic Expansions and the Maslov Index

Подождите немного. Документ загружается.

214 III,§3,2

and F is the operator with polynomial coefficients given by

FQ = F, /i +

[F2

F, and F2 being the polynomials in T given by

F1 (z)

5M2x2 Z LO +M0

F-2 (T =

(MO T2+ LO)(T2 +1).

8Lo(Lo -

Mo2)

)

2Lo(L2O

M02)

2°) Let U be a lagrangian function that is defined on the torus Y [LO, M0],

has a lagrangian amplitude Qo j6 0, and is a solution of the system

(aL2 - cL) U = (am - MO) U = 0 mod,

(2.13)

where CL is a formal number, with vanishing phase, such that

cL = L p mod

V2'

Let E be the set of points on the curve F[LO, M0] [(2.5) of §1], where

E:HQ=0.

Then

cL = Lo - 4v2 mod v,+2

and

fl(v, R, `F) = g(v, R)f(v, T) mod

vr+j,

g being some formal function with vanishing phase defined on

I'[L0, M0]\E

(2.14)

(2.15)

and f being defined as follows.

3°) There exists a unique formal function f defined on R, of the form

f (v, T) _

f, (T), where r e

(2.16)

such that

III,§3,2

215

df = 1 Ff'

(2.17)

fo = 1, fs is a real polynomial in z, of degree 3s, having the parity of s,

(2.18)

and

= 1 +

vF2(IdT

- fd

}

(2.19)

[I is the complex conjugate off ; (2.19) expresses f2s using f1,

1 f2s-11 .

Any solution of (2.17) mod(l/v') is, mod(1/v'), the product of f and a

formal number with vanishing phase.

Remark 2.

Let U' be the formal function of x that is homogeneous of

degree 0, is defined for

M0R < L0'/xi + x2,

and is given by

U v x =

f(v ) ev(LOT+Mom)

(' ) \/sinq

(2.20)

U' satisfies

(Xi-a

x2 as )U

vI2 0U' = R2

(Lo

+ 4v2) U'.

(2.21)

Proof of 1 °).

Let us calculate DL using theorem 4 of II,§3 : in this theorem

the hamiltonian L2 - Lo is substituted for H. By (3.17) of §1, the charac-

teristics of this hamiltonian are given by the equations

dt = dD = 0; that is, dR = dQ> = 0.

The parameter of these characteristics is `Y/2Lo, which is substituted for t

in this theorem. The right-hand side of formula (4.5)2 in this theorem has to

be replaced by

1/a a\l

2 r 1 /a a\ 1/a a\2l

exp2

ax' ap/ J

(x' P) = Ll

x' ap + 8 ax ap/ J

(P2R2-Q2)=P2R2-Q2-2Q-3

216

III,§3,2

This theorem gives

DLL = 2Lo

1 [x_1/2A0x1/2)

- 2

fl],

where A° is defined by (2.4) in terms of the coordinates (x1, x2, x3).

By (1.5) and (1.12) of §1, we have

R a

x a; thus R2

a22 =

2: XJxk

OR J=1 'axJ 8R

J k

8xJaxk

(2.22)

(2.23)

using the coordinates (R, T, (D) in the left-hand sides and the coordinates

(x1i x2, x3) in the right-hand sides. Then definition (2.4) of 0° is formulated

R2A-R2

2R-a.

Mk'

Now, formulas (1.5) and (1.12) of §1 give

R = - sin O cos `P, where cos O =

by §1, (1.11);

hence, on V,

'1'

R 2 T

Cot

2 O

J =

) =

\ /

R20'P = cot

cot201

sin2'P

(2.24)

The expression for R 2 t acting on functions of (R, `P) follows. Substituted

into (2.24), it gives

0° =

C1 +

Cot 2

T a.j

+ cot `P1 - sm2 P)

(2.25)

on these functions; hence, from (2.6),

X-112Ao(NX112) = ,/sin `P Do (1V

I sT.

-2L°dTFfl

+ a13,

(2.26)

by a trivial calculation. Thus (2.12) follows from (2.22).

III,§3,2

217

Proof of 2°).

By lemma 2.1, /3 locally depends only on the variables

(R, `P). By this lemma and (2.12), fi° depends only on R; by (2.5), )3o is not

identically zero.

For r = 0, 2°) is evident. Proceeding by induction on r, we can assume

that P°,

... , Pr_, are

polynomials in r whose coefficients are functions of

R and that 2°) is true when r is replaced by r - 1. Then

4v2 +

v0Lr+1 modv,l

where L,+1 E C;

L°

thus equation (2.13)1 may be written

r+1

Vc# +

4i,2

2Lr+1

33 =

mode,+2

(2.27)

By the induction hypothesis, this equation holds mod(1/v'+ 1); thus, by

(2.12), it may be written

duir = (Fflr_ ) dT + L,+ 1 fo dT for R = const.

Then, since F is an operator with polynomial coefficients, fl, is the sum of

a polynomial in T = cot W and the function Lr+ 11

P, where f

# 0. But

13r is a function of IF with period 21r. Hence

Lr+ 1 = 0,

Fir

is a polynomial in T;

thus (2.27) may be written

df3 =

(FfJ) A mod v,l

for R = const.

If 3°) is true, (2.15) follows.

Proof of 3°). The condition that (2.16) satisfy (2.17) mod(1/v') may be

written

fo = const.,

df,

= Ff,-1 for s = 1, ... , r - 1.

Thus f, is a polynomial of degree 3s in r containing an arbitrary constant

of integration. Then f is well defined up to multiplication by a formal

number with vanishing phase.

Let us choose the constants of integration to be real. Then the f, are real.

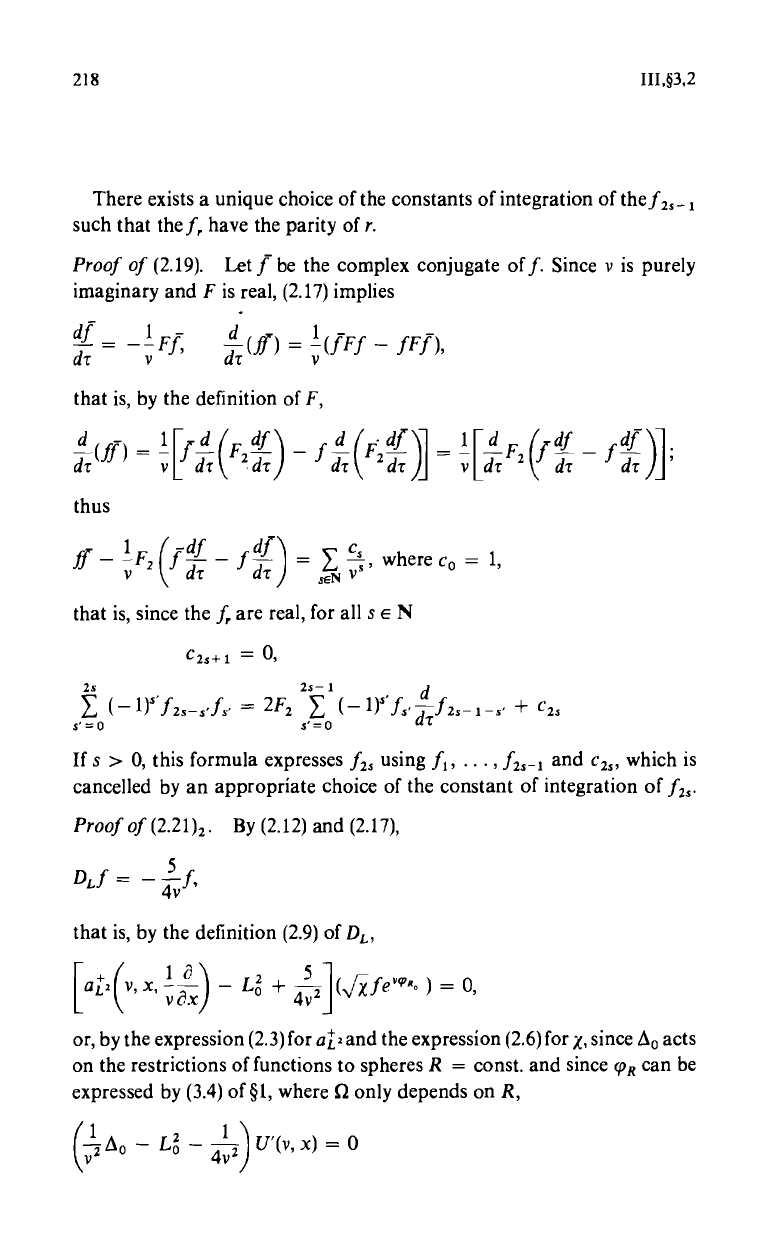
218 III,§3,2

There exists a unique choice of the constants of integration of the f

2,- 1

such that the f, have the parity of r.

Proof of (2.19).

Let f be the complex conjugate off. Since v is purely

imaginary and F is real, (2.17) implies

FI,

(f) =

(IFf - fFf

that is, by the definition of F,

d(ff)=

(F2L)

-fdCF2df

1[WdT

F2Cf4I

- fdlll.

dT v dT

A dT v

dT JJ

thus

df c

where co = 1,

T -

S E N V

seN

that is, since the f, are real, for all s e N

c2s+1 = 0,

2s-1 d

2F2 Y (-1)sf,'dTf2s-1-s' + C2,

s =o ,'=o

If s > 0, this formula expresses f2s using f1,

... ,

f2s-1 and c2s, which is

cancelled by an appropriate choice of the constant of integration of f2,.

Proof of (2.21)2.

By (2.12) and (2.17),

DJ 4vf'

that is, by the definition (2.9) of DL,

[a2(vx,

- L+

1(ffe^)

or, bythe expression (2.3) for at= and the expression (2,6) for x, since Do acts

on the restrictions of functions to spheres R = const. and since cpR can be

expressed by (3.4) of §1, where Q only depends on R,

CV2

Do - Lo - 4v2} U'(v, x) = 0

III,§3,2

219

where U' is defined by (2.20); U' is homogeneous of degree 0 in x; (2.21)2

follows from this by the definition (2.24) of A0.

Proof of (2.21)1.

From the definition (2.16) off and the expression (2.10)

for DM it follows that

DMf = 0,

or, by the definition (2.8)-(2.9) of DM,

(a+ - Mo)(f

.fe"w"")

= 0.

In the beginning of section 2, we obtained

xl -

X2 -

+ 1(

8x J

Thus a;, annihilates functions of the single variable R. Then by the

expression (2.6) for X and the expression (3.4) of §1 for (PR., the preceding

relation is equivalent to (2.21)1.

LEMMA 2.3. There exists an operator D, acting on formal functions g

defined on ['[LO, Mo]\E, such that

DH[f(v, `P)g(v, R)] _ .f (v, `V)Dg(v, R).

(2.28)

Locally,

D. R, , (2.29)

where DS(R, d/dR) is a differential operator defined on ['[L0, M0]\E and

Do = RHQ

Proof. Since DH commutes with DL, which is expressed by (2.12),

d'I'

DH [ f (v,'I')g(v, R)]

= DH

[dz

O-T

- 1

F .f (v, `')g(v, R)0.

d`I' v

(2.30)

Thus by lemma 2.2,3°), DH[ fg] is multiplication of f by a formal function,

which is defined on ['[L0, M0]\E and denoted Dg.

220

111,§3, 2

Theorem 4 of II,§3 proves that D has the form

DH =

DH,., (R,

8R ,

8`I')

sGN

where DH

is a differential operator. It follows that D has the form (2.29).

Since the characteristics of H satisfy (2.14) of §1, the same theorem proves

that

D1(fg)dt = d(fg) mod I

for dR = RHQdt, dP = HLdt.

But

f=1mod!;

thus

DNg = RHQ dR mode.

This relation is equivalent to (2.30).

THEOREM 2.

10) Problem (2.1)r, defined at the beginning of section 2, is

solvable if and only if

=Lo -4v2,

cm =Mo.

2°) Problem (2.1), is equivalent to problem (2.31)r, which is stated as

follows: To define a formal function mod(1/vr+1) on F[Lo, Mo]\E,

g(v) _

gs, where go = 1,

gs: F[Lo, Mo]\E -+

sEN V

such that

Dg = 0

mod(1/vr+'),

(2.31)r

(HQ)3rg is regular, mod(1/vr+1), on F[Lo, Mo].

Any formal function satisfying condition (2.31)r is, mod(1/vr+l), the product

of g and a formal number with vanishing phase.

The condition that g be a solution to (2.31)r evidently is equivalent to the

following :

III,§3,2-III,§3,3

221

g is a solution of problem (2.3

RHQdg,/dR + E;=1 D,g,-,

= 0 on r[L0, M0]\E,

(2.32),

(HQ)3rg, is regular on r[Lo, M0].

On r[L0, M0]\E, define the formal function

e"n

U"(v) =

/R3HQ,

where S2 is defined by (2.8) of §1. Define U' by remark 2 and lemma 2.2. Then

U'(v)U"(v) is the expression URo of a solution U of problem (2.1)r. Every

solution of the system (2.1), defined on V[LO, M0] is, mod(1/vr+l), the

product of that solution and a formal number.

3°) Suppose that g is a solution of problem (2.31)r_1. Then there exists a

function gr: r[L0, MO] \i -* C satisfying (2.32) where r is replaced by

its universal covering space 1'". The function g, is defined up to an additive

constant; moreover, gr is defined on F[L0, Mo]\E if and only if the equivalent

problems (2.1), and (2.31), are solvable.

Proof of 1°).

Use lemmas 2.1,2°) and 2.2,2°).

Proof of 2°).

Use (2.6), (2.8), lemmas 2.1,2°), 2.2,2°), and 2.3, and theo-

rems 5 and 7.2 of II,§3.

Proof of 3°). Use the above theorems.

3. A Special Case

In order to supplement theorem 2, choose

H[L, M, Q, R] = 2 {P2

K[R, M] 5

2RZ {L2 + Q2 - K [R, M] }

as in §1,4, and choose K to be an affine function of M. Then condition (1.1)

is satisfied. By (4.5) of §1, the expression in Ro of the operator associated to

His

2v2A - 2RZKLR,v(x18x-

x2i?x)j. (3.2)

222

III,§3,3

Moreover,

Lo + Q2 - K[R, Mo] = 0 on the curve I,[L0, Mo]. (3.3)

E is the set of points on this curve where Q = 0.

LEMMA 3.

We have

D R [dR

where G acts on functions

g:11[Lo, Mo]\E -+ C

and is given by

Gg=G19+dR[G2dR]

G1 and G2 being functions defined on I'[L0, Mo]\E given by

Gl(R, Q) =

GQR),

G2(R, Q) _

-2

Q ,

(3.6)

where

G3(R) =

32R(KR)2

g(K

- L2)(KR + RKR2).

Proof.

The operator D may be described as follows with the aid of II,§3,

theorem 4: in formula (4.5) of this theorem, s = 2 and

P2;

(3.7)

H(2)(X'

P) =

[

eap

2 ox ap

the equations (2.14) of §1 giving the characteristics imply that

dR =

dt, d'1' = L0 dt;

then, by the definition (2.9) of D11, when /3 only depends on the coordinates

(R, Yf) of V, this theorem gives

DH/3dt = d/3 +

-1 X-1r2A(fX112)dt

I1I,§3,3

223

for dt, dR, and d`' satisfying (3.8); in other words,

/3 Q

/ _LO

DHR

OR R + 8YJ RZ

2vX '120(QX'n

By (2.6)

x = [QR sin IF sin O]

O = const.;

therefore, by the definition (2.24) of Do, which acts on the restrictions

of functions to spheres R = const.,

112 0(flX112)

= RZ

sin

is-in -IF

+ R(8RZ

OR)(/QR).

Replacing Do by its expression (2.26) and substituting the result into

(3.9) yields

l -

QoQ

R OR + 2v

(8R2

+ R

LzdT(8

1 )1

+R d'Y

vF+8vR 2

Choose

)(v, R,'1') = f(v,'Y)g(v, R),

where f is the formal function of 'Y defined by lemma 2.2 and g is a formal

function defined

obtain

DH(fg) = fDg

with

_ Q 9

Dg _

IdR +

on I'[L0, Mo]\E. In accordance with lemma 2.3, we

2v IQ

(RZdRZ + 2R dR/ (

QR)

+ 8v

QR1.

By a trivial calculation, we deduce the expression (3.4) for D, with G

expressed by (3.5) and G1 and G2 given by

_1d RdQ

1R dQz

__1R

4 dR

[QZ dR + 8 Q3 (dR)

2 Q