Leray J. Lagrangian Analysis and Quantum Mechanics: A Mathematical Structure Related to Asymptotic Expansions and the Maslov Index

Подождите немного. Документ загружается.

154

II,§4,1

Remark 1.4.

Suppose the matrices b and is are self-adjoint. In particular,

this is the case when the matrix a is self-adjoint, that is, when

a' = (an,,)*

dm, n.

Then the values of J are purely imaginary, since it is possible to choose

9 = f

Proof of the theorem.

Part 1 follows from §3, theorem 4. To prove part 2,

let

a = aR,

(P = (PR(X),

(

x, 1Pz),

nz =

P=N.

a9n(x, P)

= w:

so that

abm

+ E b (

ax`

px,x;,

J=1

L 9P,(Pxix"

-'9;

- 9Xt

j=1

(1.9)

where x' and p; are the components of x and p (1, j = 1, ... , 1). By the

definition of a+ in §1, (6.3)-(6.6),

m (V,

V ax

e"'bn (x, Pz)am + eV

+ (2

bnP,P;(Px'x' +

bn ;Pl + cn I or.

mod

hence, by (1.9) and the definition (1.2) of L 1,

\g, L1(X' ax) a)

9nbnpl aXm +

Qn( I

npj +

J,m,n

m.n V

Thus, by choosing am = If,,, it follows from (1.5) that

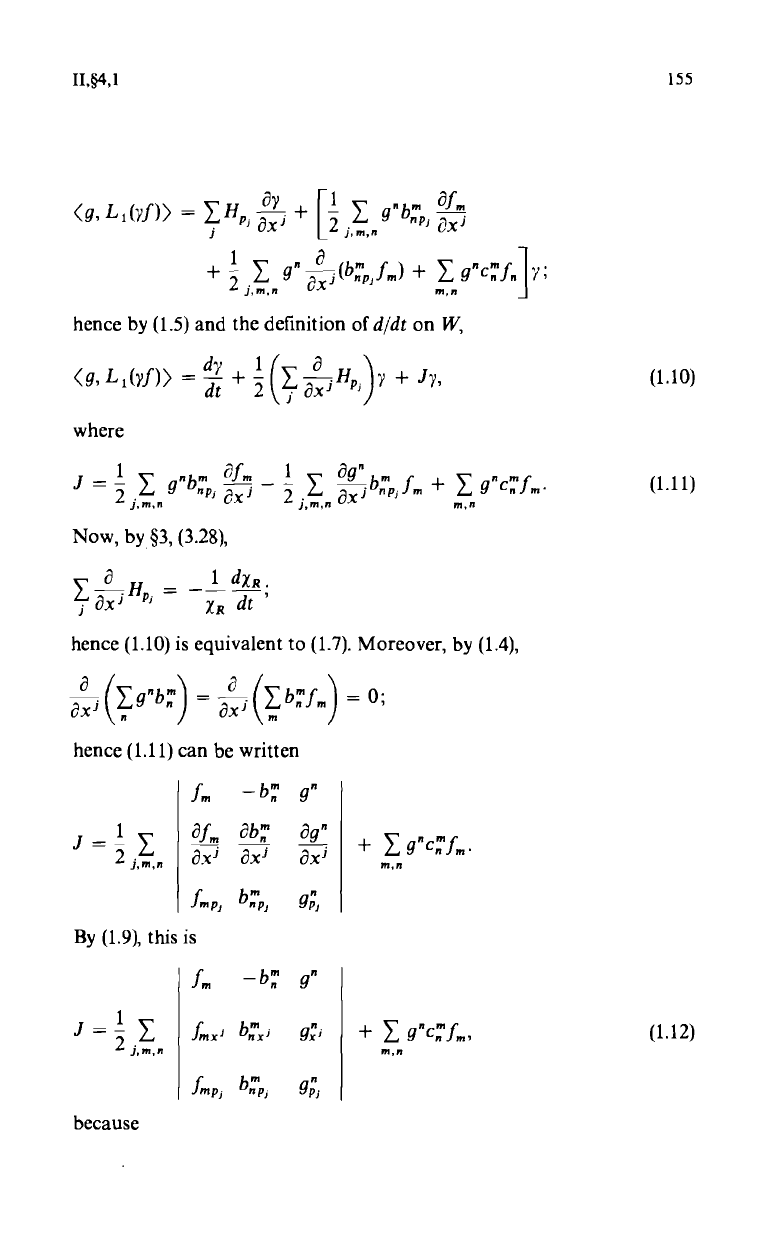
11,§4, 1

<9,Lj(yf)>

=YHp+[2I

Y-

;n9nbp'-xm

2im,n9nasi(bv;fm)+

E9ncnfnl ;

hence by (1.5) and the definition of d/dt on W,

<9, LI(yf)> = do + 2 E

aa;xp;y

+ Jy,

where

E 9nbnp

; 2 Y axjbnp fm +

9nCnfm

j, m, n j, m, n

M' n

Now, by §3, (3.28),

a 1

dx1e.

Hpj

Y-

ax,

hence (1.10) is equivalent to (1.7). Moreover, by (1.4),

axj

(Yg-b-)

I = 0;

hence (1.11) can be written

_ bn m

J = 1

Y-

2 j m n

afm ab

axj

m p; np;

By (1.9), this is

-bm

J=1

Y-

2j,mn

,nx'

nx'

m p

n p;

axj

9v,

9xn'

n m

9 Cn fm-

m,n

n m

+ 9 Cn fm,

m,n

155

(1.10)

(1.12)

because

156

II,§4,1-II,§4,2

m n

r"PI

bnpi

gPl

Jmpr

bnp 9;;

(Px'x' = 0,

since the above determinant is an antisymmetric function of (i, j). Clearly,

(1.12) is equivalent to (1.8).

Proof of remark 1.1.

(1.8) can be written

fm-11

J =

2 [(9n,

9n(bf, Jm)] + E 9ncm

m,n m,n

Now, by (1.4) there exist regular functions F. such that

Ybnlm = HFn.

Hence, on W, where H = 0,

J =

d9n +

fm)J +

9ncmfm;

m,n

thus J only depends on b, c, f, and the restriction of g to W.

2. Resolution of the Lagrangian System aU = 0 in Which the Zeros of

det a°° Are Simple Zeros

Section 5 of §3 is easily extended in this case.

Notation 2.

Notation 1 is kept. By theorem 1,1°), solutions of the system

t a' U.

= 0

(2.1)

M=1

are defined on lagrangian manifolds V in the hypersurface W given by

the equation

W : H = 0, where H = det b (by assumption, H.

0 on W). (2.2)

Let

1 N

UR =

OfR,,e

reN

II,§4,2

157

be the expression, in a frame R, of a solution

U=(U1,...,U")

of the system (2.1), which will be written

aU = 0;

the U. are lagrangian functions defined on V c W; the a,,r are functions

V\ER -+ C". In view of theorem 1, the condition aU = 0 on V\ER may

be written

Lo(x)aR,r(x) +

L, x' Oz)

xR,

s(x) = 0

Vr e N. (2.3),

s= 1

By (1.6), it implies

9(x, PR,x),

)R.Sx))

= 0. (2.4),

Y-

S=1

Let M 0 be one of the matrices V - C"x" such that the relation

Lo(x)a(x) = a'(x), where <g(x, (PR,..), a'(x)> = 0 and a(x), Y(x) c- 0.

is equivalent to the existence of y : V\ER -* C such that

a(x) + Y(x)f(x, (PR.x) = M0(x)a'(x).

Then, under condition (2.4),, equation (2.3)r may be written

aR,r(x) + YR,r(x)f(x, (PR,.) + I Mo(x)L., (X,

X)aR,r-s(x) = 0, (2.5),

s= 1

and, by (1.7), equation (2.4)r+1 may be written

(YR,rXR 112) + JYR,rXR

112

9(x, (PR,x),

E Ns+

)

XR-

Ox)aR,r-s(x

1J2

3=1

where

= 0, (2.6)r

N3+1 Cx, ax) a(x)

L 1

Cx,

)[M0(x)L(x.

)(x)]

- Ls+1

a(x).

158

II,§4,2

Theorem 2.2 in §2 supplements equations (2.5), and (2.6), as follows (r e N):

aR.,XR

3P-1/2 and thus

YR,,XR 3r-"Z are infinitely differentiable on f/, (2.7),

even at the points of tR; recall that XR' = 0 on ER.

Lemma 5 of-§3 is easily extended. It shows that the conditions (2.5),,

(2.6) and (2.7), make it possible to solve the system aU = 0 using a single

frame R. More precisely (compare §3, theorems 5 and 6), the following

theorem holds.

THEOREM 2.1.

Let V be a lagrangian manifold in the hypersurface W

defined by (2.2); let V be its universal covering space. Let R be a frame.

Let n = xRd'x be a positive invariant measure on V; assume that xR' does

not vanish to infinite order on ER ; assume that ER is transverse to the

characteristics of W that generate V. Then

UR = Y

1IR ,e'9

rEN

V r

is the expression in R of a lagrangian solution U = (Ul, ... , U"), defined

on V [or on V], of the system aU = 0 if and only if, for every r E N,

the vectors OCR, : V\tR -+C" and the functions YR,, : V\ER -. C satisfy

the conditions:

(2.5),,

(2.6),,

(2.7),

[and

YR,e"ow.: V\'R _' C]

Remark 2.

This theorem applies to solutions of the system

aU = 0

model,.

They are defined mod(1/vs+') up to the addition of where

ae'-O-: V -. C" [or V -+ C"].

Evidently we have the following theorem.

THEOREM 2.2. [Reduction mod(1/v2) of a system to an equation]

keep the assumption of theorem 1, 2°), which defines H and J. The existence

of a solution on V c W [or on V] of the lagrangian system

aU = 0

mod-, that is, an Um = 0 mod -, (2.1)2

II,§4,2-II.§4,3 159

is equivalent to the existence of a solution on V [or V] of the lagrangian

equation

a' U' = 0 mod

12 ,

where a' is the lagrangian operator associated to the formal function

To each solution U of the system (2.1)2 there corresponds a solution U'

of the equation (2.8) such that

U = U'f mod

In chapter IV, a reduction theorem analogous to the preceding one

will be used in the special case of Dirac's equation.

3. A Special Lagrangian System a U = 0 in Which the Zeros of det ao

Are Multiple Zeros

The following extension of theorem 7.1 of §3 is used in chapter IV. (Theo-

rem 7.2 of §3 admits an analogous extension.)

THEOREM 3.

Let a(k) (k = 1, . . . ,

1) be µ x µ matrices whose elements

are lagrangian operators. Assume

ac" is associated mod(1/v2)

to the matrix

H(k)E +

J(k)

where E is the µ x µ identity matrix, H(k) : 0 -. C, and j(k) : 0 - C"' is a

p x µ matrix. Let V be the manifold given by the equations

V: H")(z) = ... = Hcn(z) = 0.

(3.1)

Assume that the a(k) commute mod(1/v3) and that

dH"l) A

A dHm"

0 in a neighborhood of V.

Then the following hold.

1°) The hamiltonians HW are pairwise in involution: V is a lagrangian

manifold; the measure on V

160 II,§4,3

d 21z

dH'1' A

A dH"'

is invariant Vk under the characteristic vector x'kl of H'kl, which is tangent

to V. If V is compact, then V is a torus whose translation group is generated

by the infinitesimal transformations

2°) Let U = (U1, ... , UU) be a vector whose components U. are

lagrangian functions; U satisfies the lagrangian system

a'k) U = 0 mod ldk

if and only if U is defined on V and the lagrangian amplitudes /3 =

(/31, ... ,

of its components satisfy the system of first-order partial dif-

ferential equations

(H(k), Q)

+ J(k)$ = 0, where

Q) = ./ 4k) /3

and

is the Poisson bracket (3.14) of §3. This system is equivalent to a

completely integrable system

d/3 = w/3,

that is,

d/i = Y-wn /3m,

where the elements w' of the p x p matrix co are pfaffian forms defined

on V. In addition to (3.3), /3 has to satisfy the "quantum condition"

1/z

d`xl

/3e"°w': VEER - C°

Remark 3.

The condition that (3.3) be completely integrable may be

stated as follows:

dw=wna,

where CO A w is the matrix whose elements are the Y wh

h=1

satisfied; it is equivalent to

(H(`', J(k') - (H'k' J''') + j(i)j(k) - J'k) J(n = 0

Vi, k,

where by assumption (H'`', H(k') = 0, and by definition

(3.6)

A (am, . Hence it is

(H')J(kl) _ Y H(') j(k) _

H'',

j=1

J(k)

j=1

x' pj

II,§4,3

161

in an arbitrary frame R; (3.6) or (3.7) is equivalent to the condition that

the a(') commute

mod(1/v3).

Proof of 1°).

Let Um(m = 1, ... ,

p) be lagrangian functions defined on

V with lagrangian amplitudes

fl,,,;

let U = (U1i

... ,

and f3 =

(/3,, . , (i ). By theorem 4 of §3,

aR+(k) CV,

v 8x)

2evw. L(k)

(XI

a mod vz

(3.8)

where L(k) is a u x p matrix whose elements are first order differential

operators; the principal part of L(k) is L,,mE, where 2,&, is the Lie derivative

in the direction of the characteristic vector x(k) of H(k) and E is the u x it

identity matrix. By assumption, the a(k) commute mod(1/v3). Thus the

L(k)(x, a/ax) commute. Thus their principal parts

commute. Therefore

the )c (k) are tangent to the manifold V given by equation (3.1). [See the proof

of theorem 7.1, 1°) of §3).]

Proof of 2°). By (3.8), the system (3.2) is equivalent to the system

L(k) (x,

ax) Q = 0

Vk; (3.9)

since the 2

commute, it is possible to find local coordinates t 1, ... , t,

on V such that

Ctk

By theorem 4 of section 3,

L(k)

(X, 8x)

J(k)

(3.10)

(3.11)

Thus system (3.9), in which the unknown function 13: V -+ C" has to

satisfy (3.5), is equivalent to the system

d/3 =w/3,

on V, where

)

Y J(k) dtk

k=1

(3.12)

162

II,§4,3

is a it x u matrix whose elements are pfaffian forms. Since the a)) com-

mute, the Lik) defined by (3.8) commute, which by (3.11) is expressed

OJ(k'

OJ(i)

+ j(i)j(k)

- J(k)Jci) = 0 (3.13)

Oti - Otk

or, by (3.12), d(w = 0.) A co. This is the condition of complete integrability

of the system (3.4). By (3.10), this condition is also expressed by (3.7).

III

Schrodinger and Klein-Gordon Equations for

One-Electron Atoms in a Magnetic Field

Introduction

Summary.

The most interesting problems in the theory of linear and

homogeneous partial differential equations are the eigenvalue problems.

Their essential feature is that they have solutions only exceptionally.

Examples of lagrangian problems having the same feature are given in

this chapter. These problems assume

1 = 3, Z(3) = X Q+ X*,

X = X* = E3 (euclidean space).

They concern the lagrangian operator a associated to some convenient

hamiltonian: this hamiltonian gives rise to a Hamilton system admitting

two first integrals defined on Z(3), namely, the length L and") one of the

components M of the vector x A p in V.

H may be the hamiltonian(2) of the nonrelativistic or relativistic electron

under the simultaneous influence of the electric field of a stationary atomic

nucleus and a constant magnetic field (Zeeman effect). Then H depends

on a parameter: the energy level E of the electron. The operator a is the

Schrodinger or (in the relativistic case) the Klein-Gordon operator. The

energy levels for which our lagrangian problems have a solution coincide

with those defined by the problems that are classically studied regarding

these operators.

The advantage of the lagrangian point of view is its simplicity. By applying

theorem 7.1 of II, §3, these energy levels are obtained in §1 by a quadrature.

The latter is easily calculated in the Schrodinger and Klein-Gordon cases

using the method of residues.

In §1, we determine solutions defined mod(1/v) on a compact lagrangian

manifold of the lagrangian system:

a U = (aL2 - const.) U = (aM - const.) U = 0 mod

(1)

V11

where aL= and am are the lagrangian operators associated to the first

integrals L2 and M. Here theorem 7.1 is applied. Three integers introduced

by the Maslov quantization,

1, m, n such that I m < I < n,

'The author uses A - to denote the vector product in V. [Translator's note]

'Or the hamiltonian of the harmonic operator: see §3, remark 4.3.