Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_227 next page >

Page 227

Suppose that

M(L)

divides

. We prove that

recognises

. Because

M(L)

divides

there is a

submonoid

and a surjective homomorphism

β: N

→

M(L)

. Let

γ: A

*→

M(L)

be the natural

homomorphism determined by the congruence

σL

. Let

α: N

→

be the embedding function that takes

an element of

and maps it to the same element inside

. We therefore have the following diagram of

monoid homomorphisms indicated using solid arrows:

By Proposition 10.2.3, there is a monoid homomorphism

δ: A

*→

such that

βδ

indicated in the

diagram by the dashed arrow. We therefore have a monoid homomorphism

αδ: A

*→

. Put

. We claim that

−1

(P)

. To see this, we calculate as follows:

where we use the fact that

−1

is the identity function on

. Thus the monoid

recognises the

language

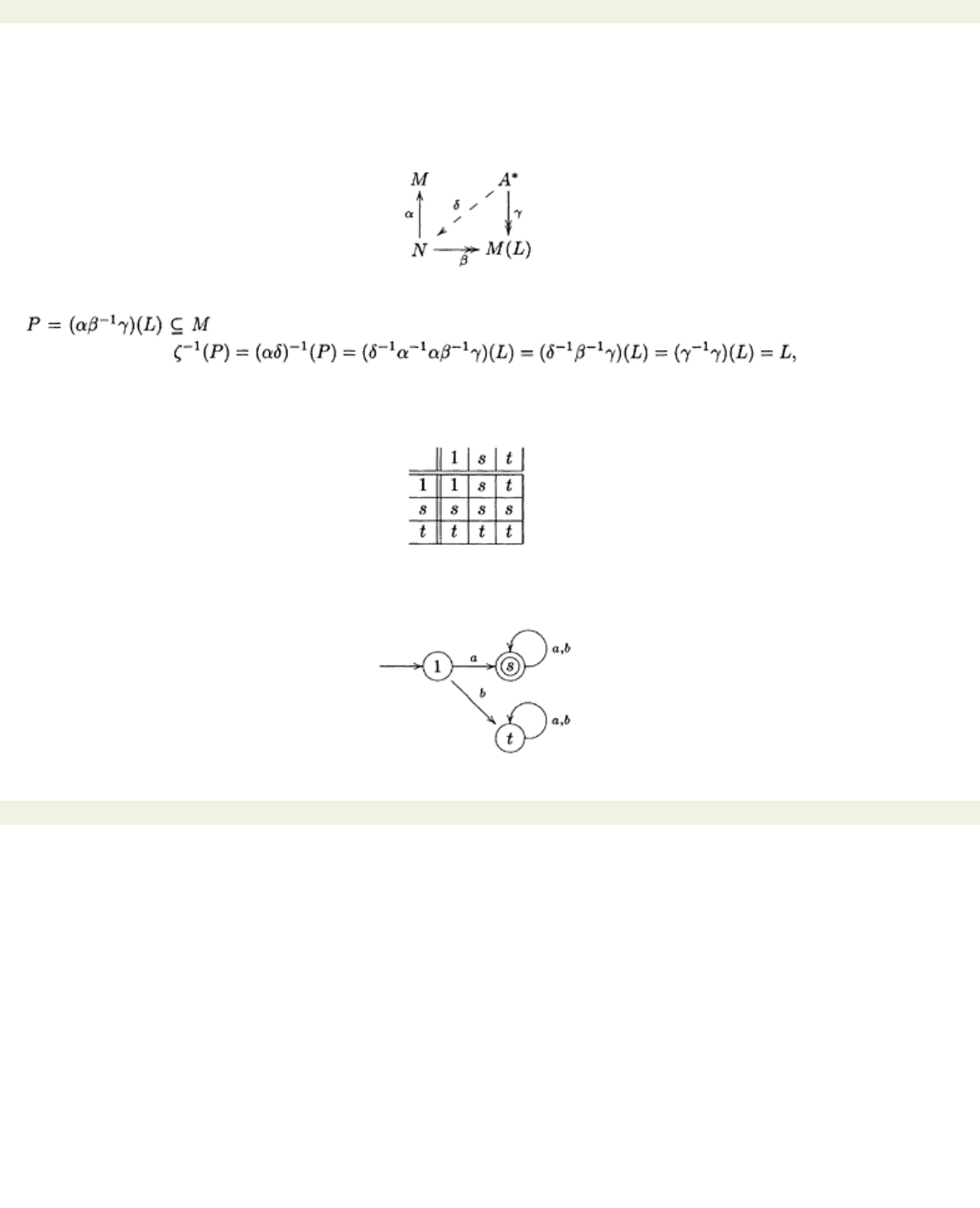
Examples 10.2.7 Here are two examples of languages recognised by monoids.

(1) Let

be the monoid with the following Cayley table:

Let

{a, b}

and define a monoid homomorphism

α: A

*→

α(a)

and

α(b)

. Then

−1

(s)

(

)*. This result can either be verified directly, or using the construction given in the proof

of Theorem 10.2.5. The automaton corresponding to the monoid homomorphism

and subset

{s}

of the

monoid

The language recognised by this machine is, by construction,

−1

(s)

< previous page page_227 next page >

< previous page page_228 next page >

Page 228

(2) Let

{a, b, c}

. Then (

+) is a commutative monoid with identity . Define by

This is a monoid homomorphism because

, and

β(xy)

β(x)

β(y)

. Let a

single element of the monoid. Then

−1

(B)

consists of all those strings in (

)* that contain both

and

but not

. Thus

−1

(B)

*. This can also be verified by constructing the

automaton from the monoid homomorphism

and subset

of the monoid using the

construction given in the proof of Theorem 10.2.5.

Some of the results we have proved about recognisable languages using finite automata can easily be

proved using finite monoids.

Proposition 10.2.8

Let A be an alphabet.

(i)

Let

If M recognises L, then M recognises L′.

(ii)

Let

If M

recognises L

and M

recognises L

, then M

1×

recognises L

and L

(iii)

Let and

If M recognises L, then M recognises u

−1

L and Lu

−1.

(iv)

Let M recognise and let α: B

*→

be a monoid homomorphism

Then M recognises α

−1

(L)

Proof (i) Let

α: A

*→

and be such that

−1

(P)

. It is easy to check that

L′

−1

(ii)

Let α

: A

*→

1 and

: A

*→

2 and and where and .

Define

β: A

*→

1×

2 by

This is a monoid homomorphism. It is easy to check that

and

(iii) Let

recognise

. Then there is a monoid homomorphism

α: A

*→

and a subset such that

−1

(P)

. We prove that

recognises

−1

. The proof of the other case is left as an exercise. Let

α(u)

. Put

< previous page page_228 next page >

< previous page page_229 next page >

Page 229

We prove that

−1

(Q)

−1

. Let . Then . Thus

;

that is . Thus and so . To prove the reverse inclusion, let

. Then

and so . Thus

which is just . Thus

and so .

(iv) Let

recognise

. Then there is a monoid homomorphism

β: A

*→

and a subset such that

−1

(P)

. Let

α: B

*→

* be a monoid homomorphism. Then

βα: B

*→

is a monoid homomorphism

and

(βα)

−1

(P)

−1

(L)

. Thus

recognises

−1

(L)

In Proposition 3.3.4, we proved that if

and

are both recognisable, then

is recognisable. To

conclude this section, we shall prove the algebraic version of this result. To do this, we shall need a new

way of combining two monoids. Let

and

be monoids and let . For each and

define

Define to consist of the following set of 2×2-matrices:

where

and . We define the product of two such matrices as follows:

Proposition 10.2.9

Let M and N be monoids. Then is a monoid.

Proof We leave it as an exercise to check that the multiplication is associative and that

is the identity, where the entry in row 1 and column 1 is the identity of

and the entry in row 2 and

column 2 is the identity of

The monoid is called the

Schützenberger product of M and N

. We shall usually denote the

elements of by triples

(m, X, n),

with the above matrix form being a useful mnemonic.

The proof of our main result depends on some calculations involving prefixes. If

is a string, we denote

by Prefix

(x)

the set of prefixes of

. If

is a prefix of

then we can write

for some string

. We

denote

−1

. The proof of the following is left as an exercise.

< previous page page_229 next page >

< previous page page_230 next page >

Page 230

Lemma 10.2.10

Let . Then

We now have our main result.

Proposition 10.2.11

Let L

and L

be languages over the alphabet A

Let M

and M

be monoids that

recognise L

and L

, respectively. Then there is a semigroup homomorphism

and a

subset Q of

such that L

−1

)

In particular, L

is recognised by a monoid that is a subsemigroup of

Proof Let

: A

*→

1 and

: A

*→

2 be monoid homomorphisms such that and and

. Define by

where

We shall prove that

is a monoid homomorphism. To do this, it is enough to prove that

for all

since this condition implies that

β(xy)

β(x)β(y)

. By definition,

By Lemma 10.2.10, this is equal to

which simplifies to

This is just

as required.

< previous page page_230 next page >

< previous page page_231 next page >

Page 231

We shall now show that if we put

β(L

)

then

−1

(Q)

. It is enough to show that

. Let . Then

β(x)

β(l

)

for some and . Thus

Now

. It follows that we can write

uv,

where and

. Thus and and so as required.

The final claim follows from the fact that the image of

is a monoid,

say, because

* is a monoid.

The monoid

clearly recognises

Exercises 10.2

1. Let be

the

function defined by

θ(n)

where and

(mod 4). Calculate

−1(2)

and

−1(

({5, 10, 15})).

2. Let

2 be the full transformation monoid on the set {1, 2}. Define elements

and of

2 as follows:

Show that

. Let

{a, b}

and define

θ: A

*→

2 by

θ(a)

and . Thus

is a

surjective monoid homomorphism. Calculate

−1

(γ),

where

3. Complete the proof of Proposition 10.2.8.

4. Prove Lemma 10.2.10.

5. Let

={−1, 1} under multiplication. How many elements does contain? How many

idempotents?

10.3 Two counterexamples

The results of this chapter have been leading us toward some kind of correspondence between finite

monoids and recognisable languages. The two counterexamples we describe in this section will therefore

appear to be a little discouraging from the point of view of setting up an ‘algebraic theory of

recognisable languages.’ However, in Chapter 12 we shall show that in fact these results simply indicate

that the algebraic theory is more subtle than might be supposed.

< previous page page_231 next page >

< previous page page_232 next page >

Page 232

Our first counterexample shows that different languages can have the same syntactic monoid. Recall

that

is the semigroup with

elements and product defined by

for all

and is the

semigroup

with an identity adjoined.

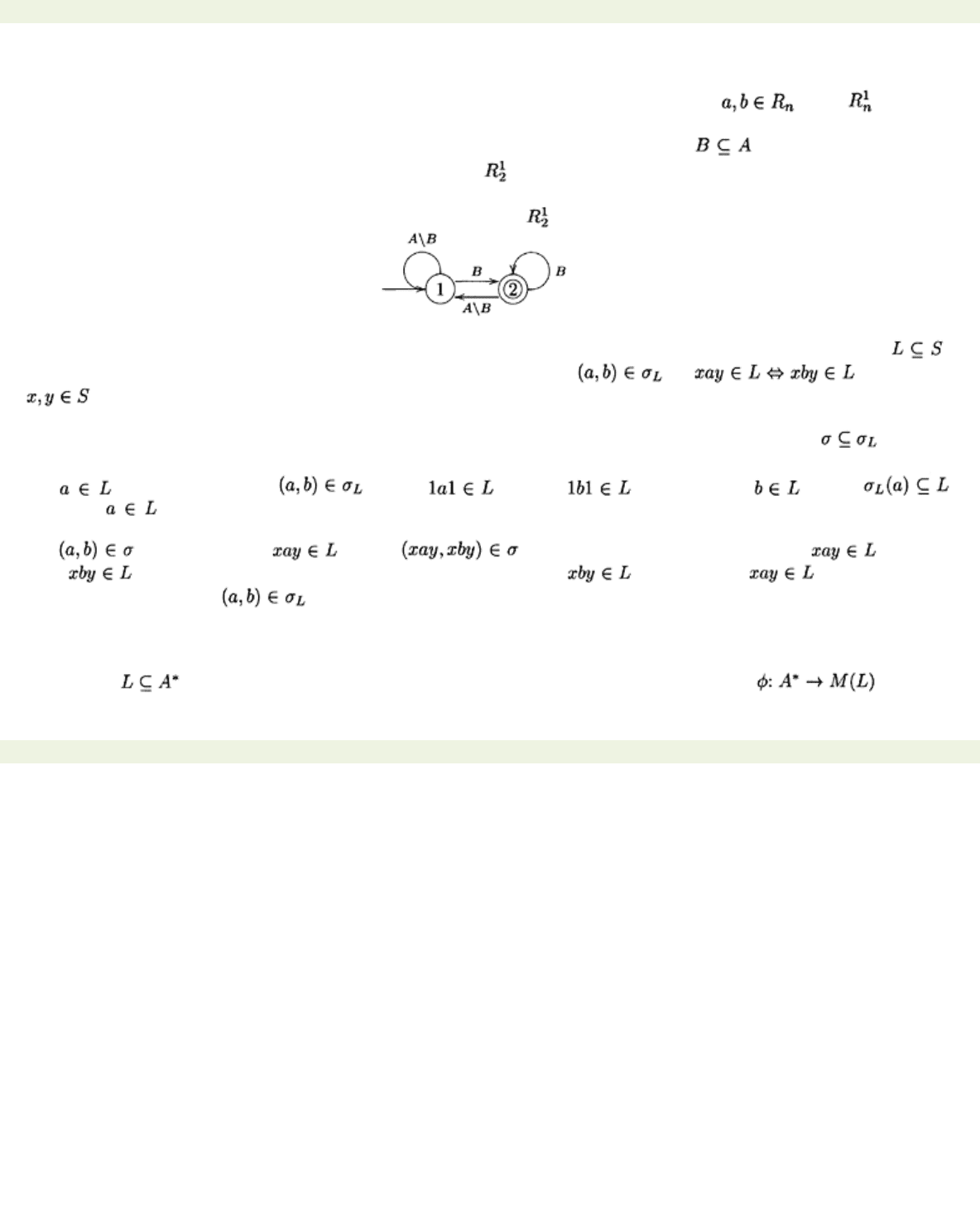
Proposition 10.3.1

Let A be any alphabet with at least two elements. Let

be any proper, non-

empty subset. Then the syntactic monoid of A

B is .

Proof It is left as an exercise to check that the automaton below is a minimal automaton for the

language

and to check that its transition monoid is .

Our next counterexample is more hard-won. First we need to extend the definition of the syntactic

congruence from subsets of free monoids to subsets of arbitrary ones. Let

be a monoid and let

be an arbitrary subset. Define the relation

σL

as follows: iff for all

Proposition 10.3.2

The relation σL is a congruence on S such that L is a union of some of the σL-

classes. If σ is any congruence on S such that L is a union of some of the σ-classes then

Proof Denote the identity of

by 1. We leave it as an exercise to show that

σL

is a congruence on

Let

and suppose that . Then and so

which gives . Thus

for each

which proves that

is a union of some of the

σL

-classes.

Now let

be an arbitrary congruence on

with the property that

is a union of some of the

-classes.

Let . Suppose that . Then because

is a congruence. But implies

that because

is a union of

-classes. By symmetry implies that . We have

therefore proved that .

A subset

of a monoid

is said to be

disjunctive

if the congruence

σL

is the equality relation.

Proposition 10.3.3

A finite monoid is the syntactic monoid of a recognisable language if and only if it

contains a disjunctive subset.

Proof Let be a recognisable language with syntactic monoid

M(L),

and let be the

natural homomorphism associated with

σL

. Put

< previous page page_232 next page >

< previous page page_233 next page >

Page 233

a subset of

M(L)

. Recall that . We shall prove that

is a disjunctive subset of

M(L)

. Let and suppose that for all we have that

We shall prove that

. Let and . We shall prove that . Suppose that

. Then and so . Thus . It follows that . By

symmetry, implies . Thus we have shown that

and so

as required.

Now let

be a finite monoid containing a disjunctive subset

. Let

θ: A

*→

be a surjective

homomorphism for some alphabet

such a homomorphism exists because

is finite and so we can

apply Proposition 10.2.2. Put

−1

(P)

. Let be the natural homomorphism associated

with the congruence

σL

. From the proof of Theorem 10.2.6, there is a surjective homomorphism

α:

→

M(L)

such that . We shall prove that

is injective. This implies that

is isomorphic to

M(L),

which will prove the result. Suppose that

α(a)

α(b)

. Let

θ(u)

and

θ(v)

. Then and so

. Suppose that for some . Let

θ(x)

and

θ(y)

. Then so that

. But so that

which implies that . Thus

implies that

. By symmetry we can prove the converse and so . But

is a disjunctive subset and so

a=b,

as required.

We have characterised when a finite monoid is a syntactic monoid. All we need now for our

counterexample is a finite semigroup that does not contain a disjunctive subset.

Proposition 10.3.4

The monoid contains no disjunctive subset for n

>2.

In particular, is not a

syntactic monoid for n

>2.

Proof Let

>2. We prove that has no disjunctive subsets. Let . We can assume that

is non-

empty because when

is empty the congruence

σP

is the universal congruence. Two elements are

σP

related precisely when they have the same contexts. So we shall calculate the possible contexts of

elements of :

• Let

where

≠1. Then iff .

• Let

. Then iff .

• Let

=1. Then iff .

It follows that

σP

can have at most three congruence classes, whereas has at least four elements

when

>2.

< previous page page_233 next page >

< previous page page_234 next page >

Page 234

Exercises 10.3

1. Complete the proof of Proposition 10.3.1.

2. Complete the proof of Proposition 10.3.2.

10.4 Summary of Chapter 10

•

Finite semigroups:

Every finite semigroup contains idempotents. The mutual divisibility properties of

finite semigroups can be displayed by eggbox diagrams. Products of semigroups are a way of

constructing new semigroups from old.

•

Recognisability by a monoid:

We can define what it means for a monoid to recognise a language as

the algebraic analogue of what it means for an automaton to recognise a language. The syntactic

monoid plays the role of the minimal automaton in the sense that it divides every monoid recognising a

given language. Some of the standard properties of recognisable languages can be proved using

monoids. The algebraic proof that the product of two recognisable languages is recognisable requires

the introduction of a new way of combining semigroups called the Schützenberger product.

10.5 Remarks on Chapter 10

This book is not primarily about semigroups, so if you want to learn more about them, then [68] or [32]

are good places to start. Two classes of semigroups have proved themselves to be particularly

important: finite semigroups and inverse semigroups. As the results of this chapter show, finite

semigroups are closely related to recognisable languages. Inverse semigroups, on the other hand, are

related to notions of symmetry. See [78] for a cornucopia of information about inverse semigroups.

The 1965 paper by Schützenberger [116] uses the notion of a language being recognised by a finite

monoid; moreover, he did something with this construction of considerable interest. See Chapter 11.

This landmark paper is also the source of the Schützenberger product of monoids. You can find out

more about this construction in [83], for example. I learnt about the results of Section 10.3 from [77].

< previous page page_234 next page >

< previous page page_235 next page >

Page 235

Chapter 11

Star-free languages

Kleene’s Theorem was the first major result on finite automata. The second deep theorem on finite

automata, due to Schützenberger, is the subject of this chapter. The set of recognisable languages is

closed under union, product, and Kleene star, and it is also closed under all the other Boolean

operations. Suppose we retain all the other operations but discard Kleene star, what can we say about

the languages that can then be described? Such languages are said to be ‘star-free.’ The goal of this

chapter is to characterise star-free languages, and the main tool we shall use to obtain our

characterisation will be the syntactic monoid of the language. Our characterisation provides conclusive

proof of the importance of the syntactic monoid in studying recognisable languages.

11.1 Introduction

Before delving into the theory, I would like to use this section to introduce the problem we are going to

solve and some of the ideas we shall use to solve it. I begin with the definition of the class of languages

we shall be interested in.

Let

be a finite alphabet. A

star-free (generalised regular) expression (over A)

is defined as follows:

(SF1)

, ε

and

where

are star-free generalised regular expresssions.

(SF2)If

and

are star-free generalised regular expressions so are

t, s

t, s′,

and

(SF3)Every star-free regular expression arises by a finite number of applications of the rules (SF1) and

(SF2).

The symbols +, n, ′, and · are called the

operators

. As usual we denote · by concatenation. Each star-

free generalised regular expression

describes a language that we denote by

L(s),

just as in the case of

regular expressions, except that we also have the symbol ′ that denotes the complement of a subset

< previous page page_235 next page >

< previous page page_236 next page >

Page 236

*. The languages

, ε,

and

where

will be called ‘basic languages.’ We say that a language

over an alphabet

star-free

if there is a star-free generalised regular expression

over

such that

L(s)

. In other words, a language is star-free if it can be constructed from the basic languages using

only the Boolean operations and the product but not the Kleene star. To help understand this definition,

we begin with an example.

Example 11.1.1 Is the language

(ab)

* star-free? On the face of it, the answer might appear to be ‘no,’

but this would be incorrect. To show that a language is star-free we have to show that it can be written

without using the Kleene star, and to show that it is not star-free we have to show that this is

impossible. Observe that a string in

(ab)

* does not contain the strings

and

as factors, and it

cannot begin with a

nor end with an

. In fact, this precisely describes the strings in

(ab)

*. Thus

and

are sets, then we can rewrite

Y′

. Clearly we can rewrite

* as . If we make these

changes in our expression above, we see that

(ab)

star-free.

This example shows that determining whether a recognisable language can be described by a star-free

regular expression may be no easy matter. To gain some insight into this problem, therefore, we shall

begin by restricting our attention first to the simplest class of recognisable languages: those over one-

letter alphabets. Let

{a}

. We know from Theorem 5.2.2 that a recognisable language over such an

alphabet has the form

Y(ap)

where

and

are finite languages. Our analysis of this language will

depend on whether

=0, 1 or

>1. If

=0, then

Y(ap)

is just a finite language, which is

evidently star-free. Its minimal automaton will be similar to that of the next case. If

=1, then we can

write this language as which shows that it is star-free. The corresponding minimal automaton

consists of a set of

+1 states labelled 0,…,

with the state 0 as the initial state. The transition

monoid of this automaton consists of the function mapping 0 to 0 if there is only one state, or in the

case of more than one state, all powers of the function that maps

+1 for

=0,…,

−1 and that

maps

Example 11.1.2 Consider the language

3 +

*. The minimal automaton for this language is

Observe that

< previous page page_236 next page >