Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_257 next page >

Page 257

•

The set V is the union of sets of the form , where , ,

but

•

The set W is the union of the set

together with sets of the form

, where

, ,

, but

Proof We prove first that

Let

so that . We have to show that

(1) .

(2)

(3) .

(1) We prove that . Let be the shortest prefix of

such that . We claim

that

≠

ε:

for if it were, we would have

and so

mp=

1 for some which, by the cancellation

property for aperiodic monoids, would give

=1. Thus

≠

as claimed. We can therefore write

ra,

where and . Put . Then

We claim that

for suppose we did have . Then

mm′

for some . Thus

and

which gives

which

contradicts our choice of

. It follows that , as claimed.

(2) The proof that

is similar to the above proof.

(3) We prove that . Suppose that . Then there are two possibilities. Either

and

or and . In either case, . If

then

uyv

for some and and so

which is a

contradiction.

We now have to prove the reverse inclusion:

Let

and put . We shall prove that

by using Proposition 11.4.5.

Now implies that

where . Thus , where . Thus

. From the fact that

we may similarly show that

. Thus .

< previous page page_257 next page >

< previous page page_258 next page >

Page 258

It remains to be proved that

. So to this end suppose to the contrary that . This

means that

. Let

be a factor of

so that

uzv,

of smallest possible length such that

. Clearly

≠

since . Suppose that . By assumption and

which implies that

a contradiction. It follows that

has length at least 2.

Accordingly we can write

arb,

where and . Then since

was chosen

with minimum length. Similarly . It follows that

which is a contradiction. Hence

and we have proved the result.

We have now done most of the work needed to prove the hard direction of our main theorem.

Theorem 11.4.10

Let L be a recognisable language whose syntactic monoid M(L) is aperiodic. Then L

is star-free.

Proof Let be the natural monoid homomorphism and let

be the subset of

M(L)

such

that

. We can write

and so to prove that

is star-free it is enough to prove that each is star-free. If

=1, then this

is proved by Lemma 11.4.7. Suppose that for all

such that r

(n)

(m)

we have proved that

is star-free. The fact that is star-free now follows from Proposition 11.4.9 and Lemma 11.4.8.

Combining Theorems 11.4.1 and 11.4.10, we obtain the following.

Theorem 11.4.11 (Schützenberger)

A recognisable language is star-free if and only if its syntactic

monoid is aperiodic.

Exercises 11.4

1. Show that the syntactic monoids of the basic languages are aperiodic.

2. Let

be a finite monoid and let . Prove that the containing the element

is equal to

11.5 An example

The goal of this section is to prove that the language

)* is star-free and to find a star-free

generalised regular expression that describes it.

< previous page page_258 next page >

< previous page page_259 next page >

Page 259

In Example 9.4.5, we calculated a presentation of the syntactic monoid

M(L)

using the minimal

automaton recognising

. From the table of representatives, we see that none of them induces a non-

trivial permutation on a subset of {0, 1, 2, 3}. Thus

is star-free. We wish to determine a star-free

expression for

and this involves more work. Before dealing with this specific case, let me describe the

method we shall use. Let

be a recognisable language over the alphabet

whose syntactic monoid is

aperiodic. Let be the natural homomorphism corresponding to the syntactic congruence of

and let so that by Lemma 10.2.4. The proof of Theorem 11.4.10 tells us that

we should first write

as the union of the inverse images of the elements

since to find a star-

free expression for

it is enough to find star-free expressions for each of these inverse images. The

proof of Theorem 11.4.10 depends on ordering the elements of

in such a way that the corresponding

list of ranks is non-increasing. For each element

in the order described above, we shall apply

Proposition 11.4.9; this involves computing the sets

U, V

and

. For each of these sets we need to find

the

that satisfy the given conditions. By Lemma 11.4.8 we know that r

(n)

(m)

. Of course,

must

satisfy other conditions, but the rank condition limits our choice and therefore the amount of work we

have to do. The other conditions that

must satisfy involve Green’s relations. It is clear, therefore, that

our first step in finding a star-free expression for our given

should be the computation of the egg-box

diagram of

M(L)

. Here is the egg-box diagram of

M(L)

where

)*:

Denote the

σL

-class containing

[x]

. We have that

where I have listed the elements in non-increasing rank order. Thus

To find a star-free expression for

it is enough to find a star-free expression for each of these four

languages.

(1)

The language .

This can be calculated using Lemma 11.4.7. We easily find in this case that

< previous page page_259 next page >

< previous page page_260 next page >

Page 260

(2)

The language .

We use Proposition 11.4.9. We know that we can write

Thus we have to calculate

U, V,

and

. It is here that we have to use the egg-box diagram. We shall

use

and

to denote elements of

to avoid confusion. Put

[ab]

We need to find and such that

Also r

(n)

(m)

. The only possibility for n is therefore

[ε]

. Thus

. It follows that

We need to find and such that

Once again r

(n)

(m)

. The only possibility for

is therefore

[ε]

. Thus

. It follows that

This breaks down into two parts, which I shall call

1 and

2, respectively. First we calculate

Now both

M[a]M

and

M[b]M

contain

[ab]

. It follows that . We now turn to

2. This involves

looking for the sets

, where

Again r

(n)

(m)

. The only possibility for

[ε]

. We now need to find the values of

and

that the triple

(c, [ε], d)

satisfies the conditions above. There are four cases to check, and we quickly

find that the only possible values of

(c, n, d)

are:

(a, [ε], a)

and

(b, [ε], b)

. Thus

Putting all these calculations together we obtain

< previous page page_260 next page >

< previous page page_261 next page >

Page 261

(3)

The language .

The calculations for this case are similar to the calculations in (2) above with

the roles of

and

interchanged. Thus

(4)

The language .

Once again we have to calculate the sets

U, V,

and

. I shall leave it as

an exercise for you to check the following:

Make the following definitions:

•

(ab)

•

(ba)

•

a(ba)

•

b(ab)

Then

Rb, V

bS,

and

aXa

bYb

. Thus

11.6 Summary of Chapter 11

•

Star-free languages:

A language is star-free if it can be constructed from finite languages using the

Boolean operations and product but not Kleene star.

•

Groups:

A group is a monoid in which each element has an inverse. A group with exactly one element

is said to be trivial. A group in a semigroup is simply a subsemigroup that is also a group.

•

Aperiodic monoids:

A monoid is aperiodic if the only groups in the monoid are trivial. A submonoid of

an aperiodic monoid is aperiodic, a homomorphic image of an aperiodic monoid is aperiodic, products of

aperiodic monoids are aperiodic, and Schützenberger products of aperiodic monoids are aperiodic.

•

Schützenberger’s Theorem:

A language is star-free if and only if its syntactic monoid is aperiodic.

< previous page page_261 next page >

< previous page page_262 next page >

Page 262

11.7 Remarks on Chapter 11

The class of star-free languages seems to have first been studied by Trakhtenbrot in 1958 and

McNaughton in 1960. Schützenberger’s Theorem was first proved in [116]. The book by McNaughton

and Papert [88] gives a fascinating account of the many different, but equivalent, ways that the class of

star-free languages can be characterised. These results lead one to surmise that the class of star-free

languages is a natural one. The proof I give of Schützenberger’s Theorem is due to Perrin [100]. A short

proof can be found in [62]. The proof of Proposition 11.2.15 is adapted from [54].

There is an alternative proof of Schützenberger’s Theorem that uses completely different ideas. In

Section 1.7, I defined what is meant by a ‘semiautomaton.’ This notion underlies both finite automata in

the sense of this book and the automata with output such as the Moore and Mealy machines also

introduced in Section 1.7. Much of automata theory can be developed as the theory of semiautomata

and then adapted to deal with acceptors or automata with output. This was the approach adopted by

John Rhodes in his early work and developed with the help of colleagues and students at Berkeley. The

key theorem of the Rhodes School is the Krohn-Rhodes Theorem, which I shall briefly sketch. By using

output functions in the sense of Moore machines, it is possible to connect semiautomata in series so

that the output of one machine becomes the input of the next. Such a combination of semiautomata is

called a ‘cascade product’ and is itself a semiautomaton. We now single out two classes of

semiautomata. A

reset semiautomaton

has the property that the effect of each input letter is to act

either as the identity function on the set of states, or as a constant function. A

grouplike semiautomaton

has as the set of states a group

input alphabet

and the action of an input letter is by right

multiplication. A group

is said to be

simple

if the only normal subgroups are the trivial subgroup and

itself; normal subgroups were defined in Question 11 of Exercises 11.2. A

simple grouplike

semiautomaton

is a grouplike semiautomaton in which the group involved is simple. Finally, we say that

the semiautomaton A

covers

the semiautomaton B if B is a homomorphic image of a subsemiautomaton

of A; I shall not define this more precisely here. We can now state the Krohn-Rhodes Theorem [76]:

every semiautomaton A can be covered by a cascade product of semiautomata each of which is either a

two-state reset semiautomaton or a simple grouplike semiautomaton. Furthermore, the groups occurring

in the grouplike semiautomata divide the groups in the transition monoid of A. A proof of this theorem is

described in [54]. The Krohn-Rhodes Theorem can be used to prove the hard direction of

Schützenberger’s Theorem: if a recognisable language

has an aperiodic syntactic monoid then

star-free. The proof runs as follows. Let A be the minimal automaton for

. Then the transition monoid

of A is isomorphic to the syntactic monoid of

and so is aperiodic. The Krohn-Rhodes Theorem applies

to the semiautomaton underlying A. Because the transition monoid is aperiodic, we conclude that the

semiautomaton underlying A can be covered

< previous page page_262 next page >

< previous page page_263 next page >

Page 263

by a cascade product of two-state reset semiautomata, i.e., because of aperiodicity no groups are

involved. It is then reasonably easy to prove that

can be accepted by an automaton whose underlying

semiautomaton is itself a cascade product of two-state reset semiautomata. The proof that

is star-free

can now be completed by induction on the number of reset semiautomata involved in the cascade

representation. The proof of this can be found in [54]. The Krohn-Rhodes Theorem is important in the

study of sequential functions. I shall say a little more about this topic in the Remarks on Chapter 12.

Despite their lack of idempotents, groups are quite interesting. An introductory account can be found in

[46]. A more advanced work is Stewart [127], who explains how groups were first introduced as a tool

for studying algebraic equations.

< previous page page_263 next page >

< previous page page_264 next page >

Page 264

This page intentionally left blank.

< previous page page_264 next page >

< previous page page_265 next page >

Page 265

Chapter 12

Varieties of languages

In Theorem 9.4.3, we proved that a language is recognisable precisely when its syntactic monoid is

finite. This result opened the door to an algebraic approach to recognisable languages. In Chapter 11,

we showed that the syntactic monoid is an important tool in studying recognisable languages when we

characterised star-free languages in terms of their syntactic monoids. However, we showed in Section

10.3 that not every finite monoid is a syntactic monoid, and that different languages can have the same

syntactic monoid. What these results point us toward is this: there is a correspondence, not between

individual

finite monoids and

individual

recognisable languages, but between

families

of monoids and

families

of languages. The aim of this chapter is to explain what this means and to prove the theorem

on which it depends: the Variety Theorem of Eilenberg and Schützenberger. This theorem provides a

framework for thinking about finite monoids and recognisable languages.

All monoids in this chapter are finite.

12.1 Pseudovarieties and varieties

Proposition 10.3.4 gave us examples of finite monoids that are not syntactic monoids. However, there is

a connection between arbitrary finite monoids and syntactic monoids. To see what this is, we first need

a lemma.

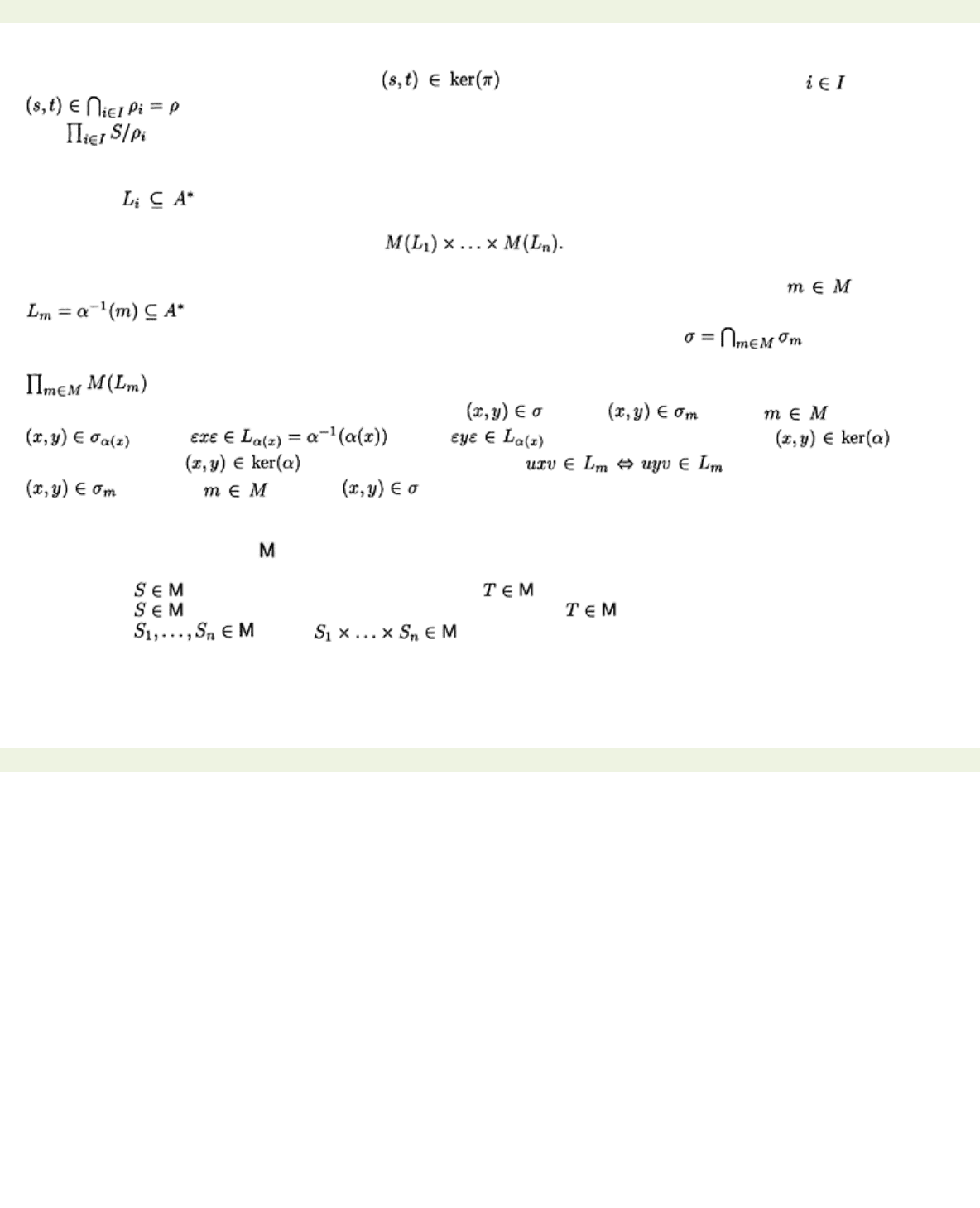
Lemma 12.1.1

Let

be a set of congruences on a semigroup S. Put

. Then:

(i)

ρ is a congruence on S.

(ii)

S/ρ is isomorphic to a subsemigroup .

Proof (i) This is left as an exercise.

(ii) Let

πi: S

→

ρi

be the natural homomorphism

πi(s)

ρi(s)

. Define by

. This is clearly a homomorphism.

< previous page page_265 next page >

< previous page page_266 next page >

Page 266

We now calculate the kernel of

. Then iff

π(s)

π(t)

iff

πi(s)

πi(t)

for all iff

. Thus ker

(π)

. By Theorem 9.2.11, there is an injective homomorphism from

into .

Our next result assuages the disappointment of Proposition 10.3.4 and points us in the right direction.

Theorem 12.1.2

Let M be a finite monoid. Then there is a finite alphabet A and finitely many

languages

, where

1≤

≤

n, such that each language Li is recognised by M, and M is isomorphic

to a submonoid of

Proof Let

be a finite monoid, in particular

is finitely generated. Thus there exists a finite alphabet

and a surjective monoid homomorphism

α: A

*→

by Proposition 10.2.2. For each , define

, which, by construction, is a language recognised by

. Let

σm

be the syntactic

congruence of

. Then

σm

M(Lm),

the syntactic monoid of

. Put

a congruence

by Lemma 12.1.1(1). By Lemma 12.1.1(ii), there is an injective homomorphism from

. To conclude the proof, we show that

=ker

(α)

which, by Theorem 9.2.11, will prove that

is isomorphic to

giving us the result. Let . Then for all . In particular,

. Now . Thus and so

α(y)

α(x),

giving as

required. Now let . It is easy to check that . It follows that

for each and so .

The theorem above highlights three operations: taking submonoids of monoids, taking homomorphic

images of monoids, and taking finite products of monoids. This leads us to the following definition. A

pseudovariety of monoids

is a non-empty collection of monoids satisfying the following three

conditions:

(VM1) If and

is a submonoid of

then .

(VM2) If and

is a homomorphic image of

then .

(VM3)

, then .

Examples 12.1.3 Here are some examples of pseudovarieties of monoids.

(1)

Finite monoids.

This is clear.

(2)

Finite aperiodic monoids.

We proved this in Theorem 11.3.4.

(3)

Finite commutative monoids.

This is left as an exercise.

< previous page page_266 next page >