Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_viii next page >

Page viii

This page intentionally left blank.

< previous page page_viii next page >

< previous page page_x next page >

Page x

and is known as

language theory

. In language theory, the simplest algorithms are those which can be

implemented by finite automata, the subject of this book.

Finite automata were first studied in the 1950s by Stephen Kleene, and found a number of important

applications in computer science: for example, in the design of computer circuits, and in the lexical

analyzers of compilers. In the 1960s and 1970s, mathematicians such as Samuel Eilenberg, Marcel-Paul

Schützenberger, and John Rhodes pioneered the mathematics of finite automata. More recently, other

mathematicians have come to appreciate the usefulness of automata in such areas as combinatorial

group theory and symbolic dynamics.

This book is intended to be an introduction to the mathematical theory of finite automata, assuming as

background only a first course in discrete mathematics. The Appendix outlines the prerequisites.

Structure of the book

The book is notionally divided into two parts: Chapters 1 to 6 form the first part, and Chapters 7 to 12

the second; Chapter 7 is the bridge that links them.

PART I. This centres on Kleene’s Theorem, the first major result proved about finite automata. I

describe two different ways of proving this theorem with Chapter 1 common to both:

• The quickest route to proving Kleene’s Theorem is the following: Sections 3.1–3.3 for constructions

involving non-deterministic automata, Section 5.1 for the definition of regular expressions, and then

Theorem 5.2.1 of Section 5.2, which is the proof of Kleene’s Theorem itself. Chapter 2, omitting Section

2.5, can be regarded as a collection of examples.

• The route that emphasises algorithms more than proofs is the following: Sections 2.1–2.3 for practice

in designing automata, Sections 3.1 and 3.2 for the accessible subset construction, Section 4.1 and

Theorem 4.2.1 of Section 4.2 for

-automata, Section 5.1 for regular expressions, and Section 5.3 for an

algorithmic proof of Kleene’s Theorem.

Section 2.6 on the Pumping Lemma can be read at any point after Chapter 1. Section 5.4 describes an

algebraic technique for converting automata into regular expressions based on solving equations.

Chapter 6, on local languages, describes a different way of converting regular expressions into automata

from that used in any of the above proofs of Kleene’s theorem.

PART II. This centres on the algebraic theory of recognisable languages, the main goals being

Schützenberger’s characterisation of star-free languages, and the Variety Theorem of Eilenberg and

Schützenberger. Chapters 7 and 8 have a strong algorithmic flavour, but Chapters 9–12 are increasingly

mathematical.

< previous page page_x next page >

< previous page page_xi next page >

Page xi

Chapter 7 describes how to find the smallest automaton recognising a given language. Two different

techniques are given depending on whether the language is described by an automaton or by a regular

expression. If the former, then Section 7.2 describes the algorithm for converting the automaton into a

minimal automaton. The theory of minimal automata is developed in Sections 7.3 and 7.4. If you just

want the algorithm for minimising an automaton then Sections 7.1 and 7.2 are all you need. If the

language is described by a regular expression, then there is a beautiful technique, called the Method of

Quotients, which will construct the minimal automaton directly from the expression. Unfortunately, there

are ‘issues’ connected with this method, but I have relegated a discussion of these to the end of Section

7.5.

The minimal automaton is obviously important from a practical point of view, but it is also the starting

point of an algebraic technique for studying recognisable languages. This is introduced in Chapter 8.

Here the transition monoid of an automaton is defined and an algorithm described for computing it. At

the conclusion of this chapter, semigroups and monoids are introduced.

The

point

of Chapter 8 will only become clear in Chapter 9, when we prove the algebraic counterpart of

Kleene’s Theorem: a language is recognisable if and only if its syntactic monoid is finite. The syntactic

monoid of a recognisable language is isomorphic to the transition monoid of the minimal automaton of

the language.

The main result of Chapter 9 tells us that finite monoids may be useful in studying recognisable

languages. Because of this, Chapter 10 develops the theory of finite monoids we shall need. We also

show how results about recognisable languages, which we previously proved using automata, can also

be proved using monoids.

The real justification for studying the syntactic monoid of a recognisable language comes in Chapter 11,

where we show that an important class of recognisable languages are characterised by the algebraic

properties of their syntactic monoids. Specifically, we prove Schützenberger’s Theorem: a language is

star-free if and only if its syntactic monoid is aperiodic.

Schützenberger’s Theorem opened up a whole new area of research: classifying recognisable languages

by means of the algebraic properties of their syntactic monoids. In Chapter 12, we prove the Variety

Theorem of Eilenberg and Schützenberger, which provides the template for proving results of this type.

Acknowledgements

In writing this book, I have used both original papers and textbooks. Individual debts are recorded in

the remarks at the end of each chapter, but I would like to highlight here a few books that have been

indispensable in writing my own. I learned automata theory originally from Carroll and Long [23] and

Hopcroft and Ullman [65]. Their influence will be apparent in many places, particularly in the first seven

chapters. The first edition of John Howie’s book,

< previous page page_xi next page >

< previous page page_xii next page >

Page xii

now rewritten as [68], introduced me to semigroup theory. I learned about the algebraic approach to

languages from Jean-Eric Pin’s book [103], which is a model of concision and clarity. Anyone who works

through my book will be well-placed to read Pin’s. In addition, I consulted Perrin’s lengthy survey article

[100] and Brauer’s

Handbuch

on finite automata [16] on numerous occasions. McNaughton and Papert’s

book [88] on star-free languages, despite being over thirty years old, is still inspiring.

On a personal level, I am especially grateful to John Fountain for reading an early version of the

manuscript and for making numerous suggestions that led to considerable improvements in the

exposition. I owe a further debt to John in that he taught me semigroup theory as an undergraduate,

and supervised my DPhil thesis, also in semigroup theory. Victoria Gould and Peter Higgins read parts of

the manuscript, contributed ideas, and corrected mistakes, as did Stuart Margolis, Benjamin Steinberg,

and my algebraic Scottish colleagues in St. Andrews. At CRC Press, I would like to thank editorial

assistant Jasmin Naim for being unfailingly helpful during the time I was writing the book, and Nishith

Arora, Michele Berman, Suzanne Lassandro, Evelyn Meany, Jamie Sigal and the anonymous copyeditor

for their assistance during the production stage. Needless to say, all errors remaining are my own.

Contact

Comments on this book are welcome. I can be contacted at:

m.v.lawson@informatics.bangor.ac.uk

My Website can be found at:

http://www.informatics.bangor.ac.uk/~mvlawson/

where I shall keep book-related information.

< previous page page_xii next page >

< previous page page_1 next page >

Page 1

Chapter 1

Introduction to finite automata

The aim of this chapter is to set out the basic definitions and ideas we shall use throughout this book.

In particular, we explain what we mean by a finite automaton and the language recognised by a finite

automaton. Background results from discrete mathematics are outlined in the Appendix.

1.1 Alphabets and strings

Most people today are familiar with the idea of digitising information; that is, converting information

from an analogue or continuous form to a discrete form. For example, it is well-known that computers

deal only in 0’s and 1’s, but users of computers do not have to communicate with them in binary; they

can interact with the computer in a great variety of ways. For example, voice recognition technology

enables us to input data without using the keyboard, whereas computer graphics can present output in

the form of animation. But these things are only possible because of the underlying sequences of 0’s

and 1’s that encode this information. We begin this section therefore by examining sequences of

symbols and their properties.

Information in all its forms is usually represented as sequences of symbols drawn from some fixed

repertoire of symbols. More formally, any set of symbols

that is used in this way is called an

alphabet,

and any finite sequence whose components are drawn from

is called a

string over A

or simply a

string

.1 We call the elements of an alphabet

symbols

letters

. The number of symbols in an alphabet

is denoted by |

|. The alphabets in this book will always be finite.

1 The term

word

is often used instead of string.

< previous page page_1 next page >

< previous page page_2 next page >

Page 2

Examples 1.1.1 Here are a few examples of alphabets you may have encountered.

(1) An alphabet suitable for describing the detailed workings of a computer is {0, 1}.

(2) An alphabet for representing natural numbers in base 10 is

(3) An alphabet suitable for writing stories in English is

upper and lower case letters together with punctuation symbols and a space symbol to separate

different words.

(4) An alphabet for formal logic is

(5) The alphabet used in describing a programming language is called the set of

tokens

of the language.

For example, in the

language, the following are all tokens:

(6) DNA is constructed from four main types of molecules: adenine (A), cytosine (C), guanine (G), and

thymine (T). Sequences of these molecules, and so strings over the alphabet

{A, C, G, T},

form the

basis of genes.

The symbols in an alphabet do not have to be especially simple. An alphabet could consist of pictures, or

each element of an alphabet could itself be a sequence of symbols. Thus the set of all Chinese

characters is an alphabet in our sense although it is not an alphabet in the linguistic sense, as is the set

of all words in an ordinary dictionary—a word like ‘egalitarianism’ would, in this context, be regarded as

a single symbol. An important example of using sequences of symbols over one alphabet to represent

the elements of another alphabet occurs with ASCII encoding, and also forms the basis of data-

compression and error-correction codes. You might wonder why, when all information can be encoded

in binary, we do not just stick with the alphabet {0, 1}. The reason is one of convenience: binary is

good for computers and bad for people. That said, most of the alphabets we use in this book will just

have a few elements but, again, that is just for convenience.

A string is a list and so it is formally written using brackets and commas to separate components. Thus

(0, 1, 1, 1, 0) is a string over the alphabet

={0, 1}, whereas (to, be, or, not, to, be) is a string over

the alphabet whose elements are the words in an English dictionary. The string () is the

< previous page page_2 next page >

< previous page page_3 next page >

Page 3

empty string. However, for the remainder of this book, we shall write strings without brackets and

commas and so for instance we write 01110 rather than (0, 1, 1, 1, 0). The empty string needs to be

recorded in some way and we denote it by

. The set of all strings over the alphabet

is denoted by

read

A star,

and the set of all strings except the empty one is denoted by

read

A plus

is a string then |

| denotes the total number of symbols appearing in

and is called the

length of

. If then |

is the total number of

’s appearing in

. For example, |

|=0, and |011011|=5;

|01101|0=2, and |01101|1=3. Two strings

and

over an alphabet

are

equal

if they contain the

same symbols in the same order.

Given two strings

we can form a new string

called the

concatenation of x and y,

by simply

adjoining the symbols in

to those in

. For example, if

={0, 1} then both 0101 and 101010 are

strings over

. The concatenation of 0101 and 101010 is denoted 0101·101010 and is equal to the

string 0101101010. We shall usually denote the concatenation of

and

rather than

. If

then |

|=|

|+|

;

when we concatenate two strings the length of the result is the sum of the

lengths of the two strings. The string

has a special property with respect to concatenation: for each

string

we clearly have that

εx

xε

There is one point that needs to be emphasised: the order in which strings are concatenated is

important. For example, if

{a, b}

and

then

abba

and

baab

and clearly

≠

. We have all been made painfully familiar with this fact: the spelling of the word ‘concieve’ is

wrong, whereas the spelling ‘conceive’ is correct. This is because ‘order matters’ in spelling. In the case

where

consists of only one letter, then the order in which we concatenate strings is immaterial. For

example, if

{a}

then strings in

* are just sequences of

’s, and clearly, the order in which we

concatenate strings of

’s is not important.

Given three strings

x, y,

and

there are two distinct ways to concatenate them in this order: we can

concatenate

and

first to obtain

and then concatenate

with

to obtain

xyz,

or we can

concatenate

and

first to obtain

and then concatenate

with

to obtain

xyz

again. In other

words,

(xy)z

x(yz)

. We say that concatenation is

associative

is a string then we write

, when

≥1, to mean the concatenation of

with itself n-times. We

define

. For example, if

then

(ba)

baba

. The usual laws of indices hold: if

m, n

≥0 then

xmxn

Let

. If

xyz

then

is called a factor of

u, x

is called a

prefix

and

is called a

suffix

. We call the factor

y proper

if at least one of

and

is not just the empty string. In a similar fashion

we say that the prefix

(resp. suffix

) is

proper

≠

(resp.

≠

). We say that the string

is a

substring

of the string

…an,

where

and there

2See Chapter 9 for more on associativity. Specifically, Theorem 9.1.1 is the key property of associative

operations. The proof of this result is less important than what it says.

< previous page page_3 next page >

< previous page page_4 next page >

Page 4

exist strings

,…, xn

such that

…xn−

anxn

. Let . We call a representation

…un,

where each

a factorisation of

For example, consider the string

u=abab

over the alphabet

{a, b}

. Then the prefixes of

are:

ε, a, ab,

aba, abab;

the suffixes of

are:

ε, b, ab, bab, abab;

and the factors of

are:

ε, a, b, ab, ba, aba, bab,

abab

. The strings

aa, bb, abb

are examples of substrings of

. Finally,

is a factorisation of

observe that I use the · to emphasise the factorisation.

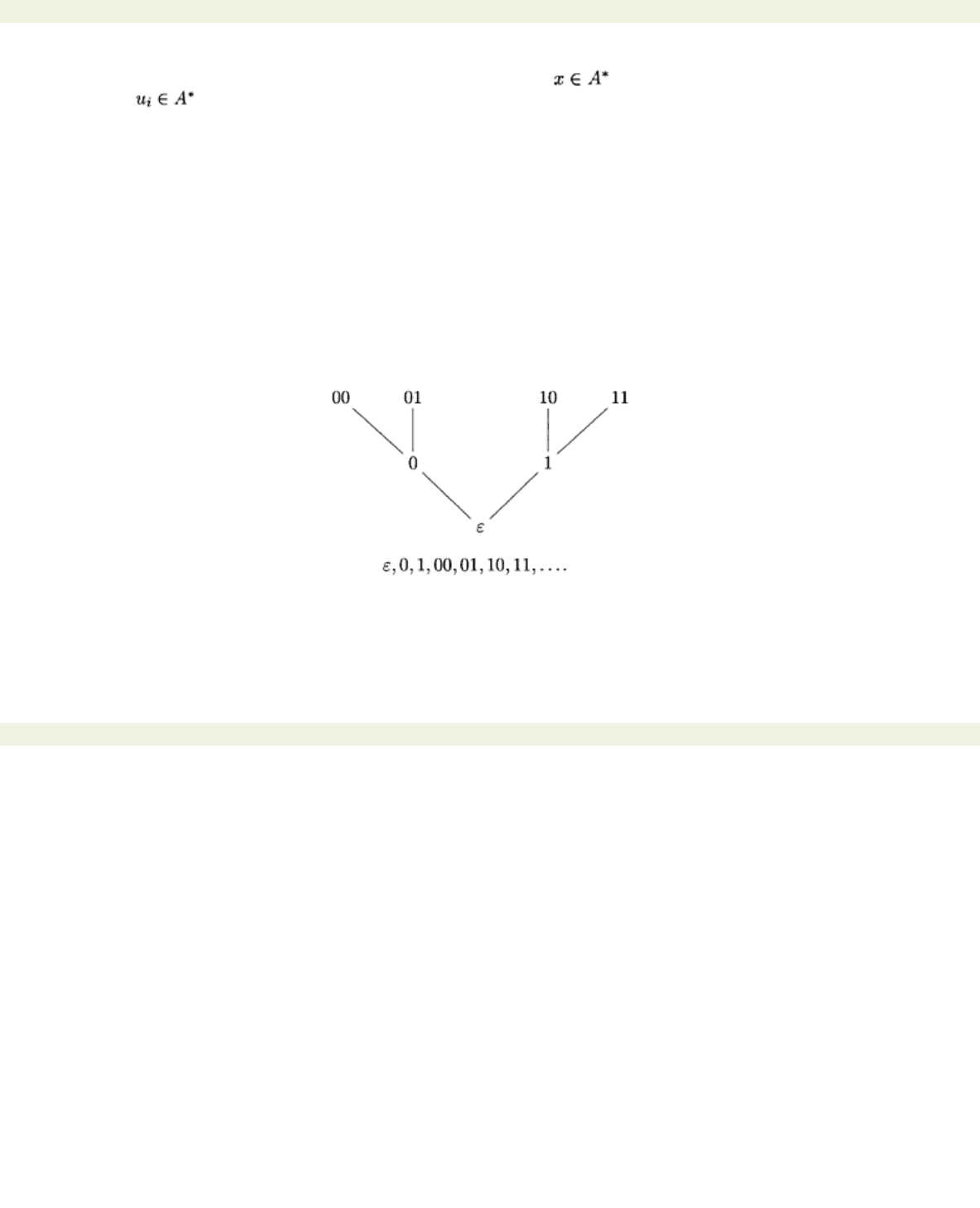
When discussing strings over an alphabet, it is useful to have a standard way of listing them. This can

easily be done using what is known as the

tree order

3 on

*. Let

,…, an}

be an alphabet. Choose

a fixed linear order for the elements of

. This is usually obvious, for example, if

={0, 1} then we

would assume that 0<1 but in principle any ordering of the elements of the alphabet may be chosen,

but if a non-standard ordering is to be used then it has to be explicitly described. We now grow a tree,

called the

tree over A

whose root is

and whose vertices are labelled with the elements of

according to the following recipe: if

is a vertex, then the vertices growing out of

are

,…, wan

The

tree order on A

* is now obtained as follows:

if and only if |

|<|

|, or |

|=|

| and the string

occurs to the left of the string

in the tree over

*. To make this clearer, we do a simple example. Let

={0, 1}, where we assume 0<1. The first few levels of the tree over

* are:

Thus the tree order for

* begins as follows

This ordering amounts to saying that a string precedes all strictly longer strings, while all the strings of

the same length are listed

lexicographically,

that is to say the way they are listed in a dictionary4 based

on the ordering of the alphabet being used.

3Also known as the ‘length-plus-lexicographic order,’ which is more of a mouthful, and the ‘ShortLex

order.’

4Also known as a

lexicon

< previous page page_4 next page >

< previous page page_5 next page >

Page 5

Exercises 1.1

1. Write down the set of prefixes, the set of suffixes, and the set of factors of the string,

over the alphabet

{a,…, z}

. When writing down the set of factors, list them in order of length. Find three

substrings that are not factors.

2. Let

{a, b}

with the order

. Draw the tree over

* up to and including all strings of length 3.

Arrange these strings according to the tree order.

3. Let

{a, b, c}

. If

in the tree order, what is the corresponding linear order for the

elements of

4. Let

be an alphabet. Prove that

* is

cancellative

with respect to concatenation, meaning that if

then

implies

and

implies

5. Let

. Suppose that

. Prove the following hold:

(i) If |

|>|

|, then there exists a non-empty string

such that

and

(ii) If |

|=|

|, then

and

(iii) If |

|<|

|, then there exists a non-empty string

such that

and

6. In general, if

then the strings

and

are different as we have noted. This raises the

question of finding conditions under which

. Prove that the following two conditions are

equivalent:

(i)

(ii) There exists a string

such that

and

for some natural numbers

p, q

>0.

You can use Question 5 in solving this problem. Proving results about strings is often no easy matter.

More combinatorial properties of strings are described in [82].

1.2 Languages

Before defining the word ‘language’ formally, here is a motivating example.

< previous page page_5 next page >

< previous page page_6 next page >

Page 6

Example 1.2.1 Let

be the alphabet that consists of all words in an English dictionary. So

contains a

very large number of elements: of the order of half a million. As we explained in Section 1.1, we can

think of each English word as being a single symbol. The set

* consists of all possible finite sequences

of words. An important subset

* consists of all sequences of words that form grammatically correct

English sentences. Thus the sequence whereas . Someone

who wants to understand English has to learn the rules for deciding when a string of words belongs to

the set

. We can therefore think of

as being the ‘English language.’5

This example motivates the following definition. For

any

alphabet

A, any

subset of

* is called an

A-

language,

or a

language over A

or simply a

language

Examples 1.2.2 Here are some examples of languages.

(1) In elementary arithmetic we use the alphabet,

We can form the language

of all correct sums: thus the sequence 2+2=4 is in

whereas the sequence

1÷0=42 is not. Any totally meaningless string such as ÷+=98= also fails to be in

(2) In computer science, the set of all syntactically correct programs in a given computer language, such

as Java, constitutes a language.

(3) Both and

* are languages over

the smallest and the largest, respectively.

Languages also arise from what are known as

decision problems,

which are problems whose answer is

either ‘yes’ or ‘no.’ For example, we can ask whether a number is prime; the answer to this question is

either a ‘yes’ or a ‘no.’ We illustrate how decision problems give rise to languages by means of an

example.

Example 1.2.3 A simple graph is one with no loops and no multiple edges. A graph is said to be

connected

if any two vertices can be joined by a path. Clearly a graph is either connected or not. Thus

‘Is the simple graph

connected?’ is an example of a decision problem. We now show how to construct

a language from this decision problem.

5In reality, membership of this set is sometimes problematic, but the languages we meet in practice will

be formal and always clearly defined.

< previous page page_6 next page >