Lawson M.V. Finite Automata
Подождите немного. Документ загружается.


< previous page page_27 next page >
Page 27
Chapter 2
Recognisable languages
In Chapter 1, we introduced finite automata and the languages they recognise. In this chapter we do
two things. First, we look at ways of constructing certain kinds of automata. Second, we describe a
technique for showing that some languages are
not
recognisable.
2.1 Designing automata
Designing an automaton A to recognise a language
L
is more an art than a science. However, it is
possible to lay down some guidelines. In this section, I will describe the general points that need to be
born in mind, and in Sections 2.2 to 2.5, I will describe some specific techniques for particular kinds of
languages.
Automata can be regarded as simple programming languages, and so the methods used to write
programs can be adopted to help design automata. Whenever you write a program to solve a problem,
it is good practice to begin by formulating the algorithm that the program should implement. By the
same token, before trying to construct an automaton to recognise a language, you should first
formulate an algorithm that accomplishes the task of recognising the language. There is however an
important constraint: your algorithm must only involve using a fixed amount of memory. One way of
ensuring this is to imagine how you would set about recognising the strings belonging to a language for
extremely large
inputs. When you have done this, you can then implement your algorithm by means of
an automaton.
Once you have a design, A, it is easy to check that it is well-formed—this is equivalent to checking that
a program is syntactically correct—but the crucial point now is to verify that your automaton really
recognises the language
L
in question. This involves checking that two conditions hold:
(1) Each string accepted by A is in
L
.
(2) Each string in
L
is accepted by A.
< previous page page_27 next page >
< previous page page_28 next page >
Page 28
I have emphasised that two conditions must hold, because it is a very common mistake to check only
(1). If both of these conditions are satisfied then you have solved the problem. But if either one of them
is violated then you have to go back and modify your machine and try again. Unfortunately, it is easier
to show that your automaton
does not
work than it is to show it
does
. To show that your machine is
wrong it is enough to find just one string
x
that is in the language
L
but not accepted by the machine A,
or is accepted by the machine A but is not in the language
L
. The difficulty is that
A
* contains infinitely
many strings and your machine has to deliver the correct response to each of them.
The minimum you should do to show that your well-formed automaton solves the problem is to try out
some test strings on it, making sure to include both strings belonging to the language and those that do
not. However even if your automaton passes these tests with flying colours it could still be wrong. There
are two further strategies that you can use. First, if you find you have made a mistake then try to use
the nature of the mistake to help you see how to correct the design. Second, try to be clear about the
function of each state in your machine: each state should be charged with detecting some feature of
that part of the input string that has so far been read. Some of the ideas that go into constructing
automata are illustrated by means of examples in the following sections. At the same time I shall
describe some useful techniques for constructing automata. Although I often use alphabets with just two
letters, this is just for convenience, similar examples can be constructed over other alphabets.
Exercises 2.1
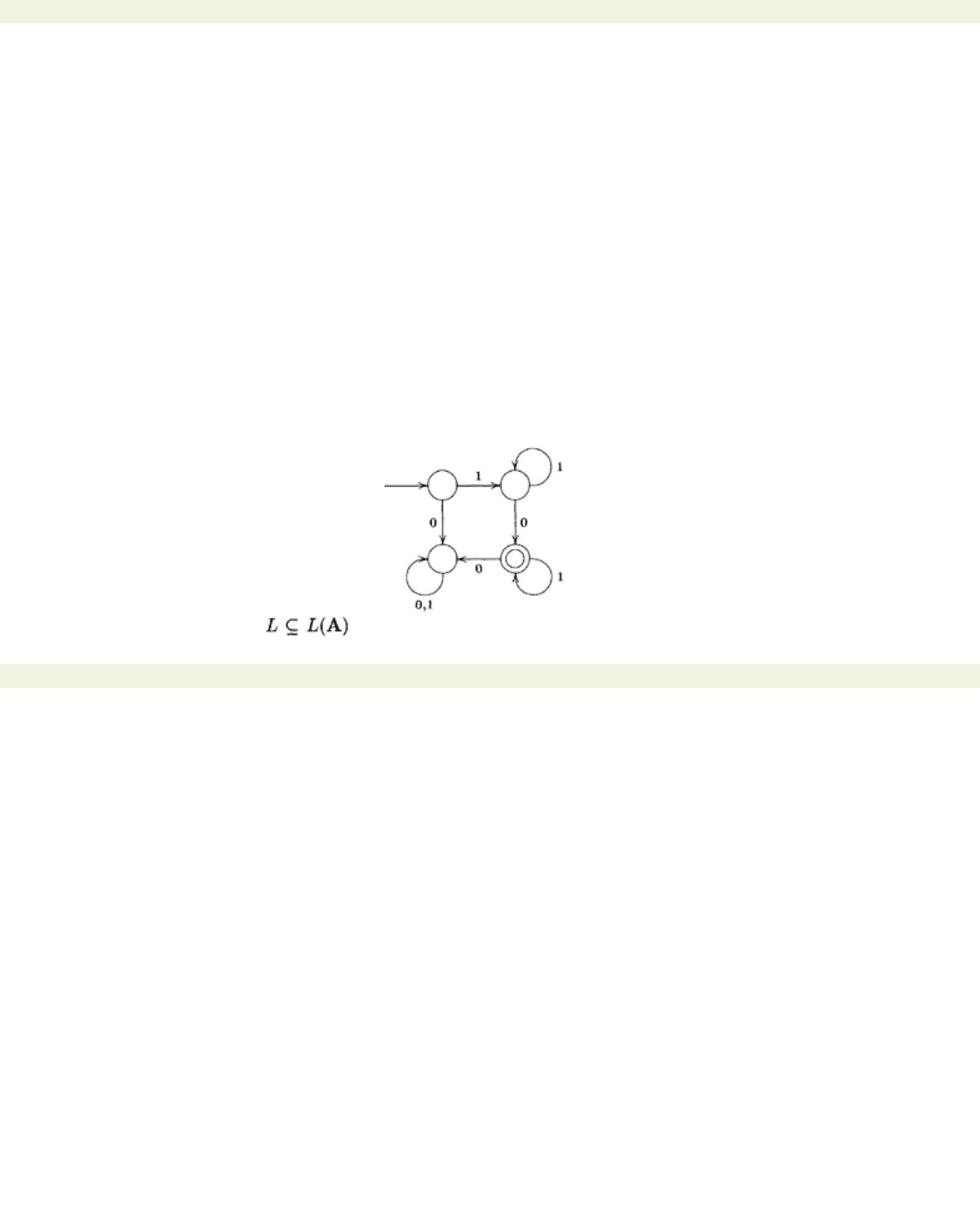
1. Let A be the automaton:
and let
L
=1+0. Show that , but that the reverse inclusion does not hold. Describe
L
(A).
< previous page page_28 next page >

< previous page page_29 next page >
Page 29
2. Let A be the automaton:
Show that every string in
L
(A) has an odd number of 1’s, but that not every string with an odd number
of 1’s is accepted by A. Describe
L
(A).
3. Let A be the automaton:
Let
L
be the language consisting of all strings over {0, 1} containing an odd number of 1’s. Show that
neither nor . Describe
L
(A).
2.2 Incomplete automata
A useful design technique is illustrated by the following example.
Example 2.2.1 Construct an automaton to recognise the language
L
=
{abab}
. We first construct a
‘spine’ as follows:
This diagram has a path labelled
abab
from the initial state to the terminal state and so we have
ensured that the string
abab
will be recognised. However, it fails to be an automaton because there are
missing transitions. It is tempting to put loops on the states and label the loops with the missing
symbols, but this is exactly the wrong thing to do (why?). Instead, we add a new state, called a ‘sink
state,’ to which we can harmlessly lead all unwanted transitions. In this way, we obtain the following
automaton.
< previous page page_29 next page >

< previous page page_30 next page >
Page 30
The idea behind the above example can be generalised. The ‘spine’ we constructed above is an example
of an incomplete automaton; this is just like an automaton except that there are missing transitions.
More formally, we define them as follows. An
incomplete automaton
is defined in exactly the same way
as a complete deterministic automaton except that the transition
function δ
is replaced by a
partial
function
. This means that
δ(s, a)
is not defined for some
;
in such cases, we say that the
machine fails.
Let A=
(S, A, i, δ, T)
be an incomplete automaton. To define the language accepted by this machine we
proceed as in the complete case, and with a similar justification. The extended transition function
δ
* is
defined as before, except this time
δ
* is a partial function from
S
×
A
* to
S
. More precisely,
δ
* is defined
as follows. Let
,
and :
(ETF1)
δ
*
(s, ε)
=
s
.
(ETF2)
δ
*
(s, a)
=
δ(s, a)
.
(ETF3)
We now define
L
(A) to consist of all those strings such that
δ
*
(i, x)
is defined and is a terminal
state.
In a complete automaton, there is
exactly one
path in the machine starting at the initial state and
labelled by a given string. In an incomplete automaton, on the other hand, there is
at most one
path
starting at the initial state and labelled by a given string. The language recognised by an incomplete
automaton still consists of all strings over the input alphabet that label paths beginning at the initial
state and ending at a terminal state.
It is easy to convert an incomplete machine into a complete machine that recognises the same
language.
Proposition 2.2.2
For each incomplete automaton
A
there is a complete automaton
A
c such that
L
(A
c
)=
L
(A).
Proof Let A=
(S, A, i, δ, T)
. Define Ac as follows. Let ∞ be any symbol not in
S
. Then will be
the set of states of A
c
; its initial state is
i
and its set of terminal states is
T
. The transition function of
γ
of A
c
is defined as follows. For each and
Because the machine A is sitting inside A
c
, it is immediate that . To prove the reverse
inclusion, observe that any string that is accepted by A
c
< previous page page_30 next page >

< previous page page_31 next page >
Page 31
cannot pass through the state ∞ at any point. Thus the string is essentially being processed by A.
We say that a state
s
in an automaton is a
sink state
if
s
·
a
=
s
for each in the input alphabet. Thus
the state ∞ in our construction above is a sink state, and the process of converting an incomplete
machine into a complete machine is called
completion (by adjoining a sink state)
. The automaton A
c
is
called the
completion
of A.
It is sometimes easier to design an incomplete automaton to recognise a language and than to
complete it by adjoining a sink state then to try to design the automaton all in one go. We can apply
this idea to show that any
finite
language is recognisable. We illustrate this result by means of an
example.
Example 2.2.3 Consider the finite language
{b, aa, ba}
. The starting point for our automaton is the
part of the tree over
{a, b},
which contains all strings of length 2 and smaller:
Notice that I have used labelled arrows rather than edges. This is used to build an incomplete
automaton that recognises
{b, aa, ba}:
the vertices of the tree become the states, the initial state is the
vertex labelled
ε,
and the terminal states are the vertices labelled with the strings in the language.
< previous page page_31 next page >

< previous page page_32 next page >
Page 32
This incomplete automaton is then completed by the addition of a sink state. We thus obtain the
following automaton that recognises
{b, aa, ba}
.
Our example of an automaton that recognises the language
{b, aa, ba}
raises another point. Another
(incomplete) machine that recognises this language is
Thus by adjoining a sink state, we need only 5 states to recognise
{b, aa, ba}
instead of the 8 in our
example above. The question of finding the smallest number of states to recognise a given language is
one that we shall pursue in Chapter 7.
The proof of the following is now left as an exercise.
Proposition 2.2.4
Every finite language is recognisable.
Exercises 2.2
1. Construct an automaton to recognise the language
2. Write out a full proof of Proposition 2.2.4.
< previous page page_32 next page >
< previous page page_33 next page >
Page 33
2.3 Automata that count
Counting is one of the simplest ways of describing languages. For example, we might want to describe a
language by restricting the lengths of the strings that can appear, or by requiring that a particular letter
or pattern appears a certain number of times. We shall also see that there are limits to what automata
can do in the realm of counting. We begin with a simple example.
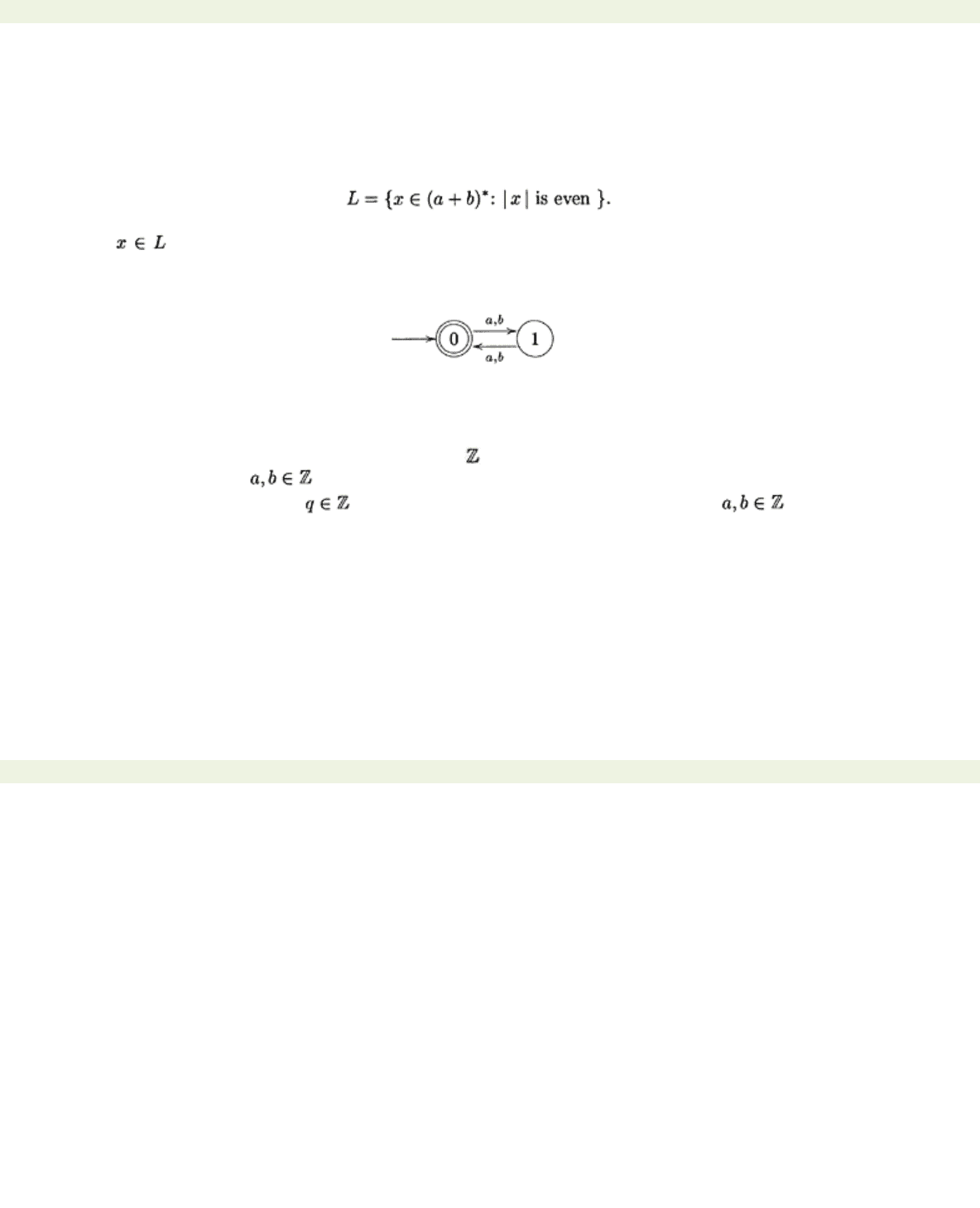
Example 2.3.1 Construct an automaton to recognise the language
The first step in constructing an automaton is to ensure that you understand what the language is. In
this case, precisely if |
x
|=0, 2, 4,…. The empty string
ε
is accepted since |
ε
|=0, and so the initial
state will also have to be terminal. In this case, we shall only need two states: one state remembers
that we have read an even number of symbols and another that remembers that we have read an odd
number of symbols. We therefore obtain the following automaton.
If, instead, we wanted to construct an automaton that recognised the language of strings over
{a, b}
of
odd
length, then we would simply modify the above machine by making state 0 non-terminal and state
1 terminal.
To generalise the above example, I shall need some terminology. The set of integers, that is the set of
positive and negative whole numbers, is denoted . The word ‘number’ will almost always mean
‘integer’ from now on. If we say that
a divides b,
or that
b
is
divisible by a,
or that
b
is a
multiple
of
a,
if
b
=
aq
for some ; this is written mathematically as
a
|
b
. If and
a
>0 then
we can write
b
=
aq
+
r
where 0≤
r
<
a
. The number
q
is called the
quotient
and
r
is called the
remainder
.
The quotient and remainder are uniquely determined by
a
and
b
meaning that if
b
=
aq′
+
r′
where 0≤
r
′<a
then
q
=
q′
and
r
=
r′
. This result is called the ‘Remainder Theorem’ and is one of the basic properties
of the integers.
Using this terminology, let us look again at odd and even numbers. If we divide a number by 2, then
there are exactly two possible remainders: 0 or 1. A number that has no remainder when divided by 2 is
just an even number and a number that leaves the remainder 1 when divided by 2 is just an odd
number. It is an accident of history that English, and many other languages, happen to have single
words that mean ‘leaves no remainder when divided by 2’ and ‘leaves remainder 1 when divided by 2.’
Now let us look at what happens when we divide a number by 3. This time there are three possible
cases: ‘leaves no remainder when divided by 3,’ ‘leaves
< previous page page_33 next page >
< previous page page_34 next page >
Page 34
remainder 1 when divided by 3,’ and ‘leaves remainder 2 when divided by 3.’ In this case, there are no
single words in English that we can use to substitute for each of these phrases, but this does not
matter.
Let
n
≥2 be an integer, and let
a
and
b
be arbitrary integers. We say that
a
is
congruent to b modulo n,
written as
if
n
|(
a
−
b
). An equivalent way of phrasing this definition is to say that
a
and
b
have the same remainder
when divided by
n
. Put the set of possible remainders when a number is divided by
n
.
Using this notation, we see that
a
is even precisely when
a
=0 (mod 2) and is odd when
a
=1 (mod 2). If
a
=
b
(mod 2) then we say they have the
same parity:
they are either both odd or both even. If a
number
a
=0 (mod
n
) then it is divisible by
n
.
Now that we have this terminology in place, we can generalise Example 2.3.1.
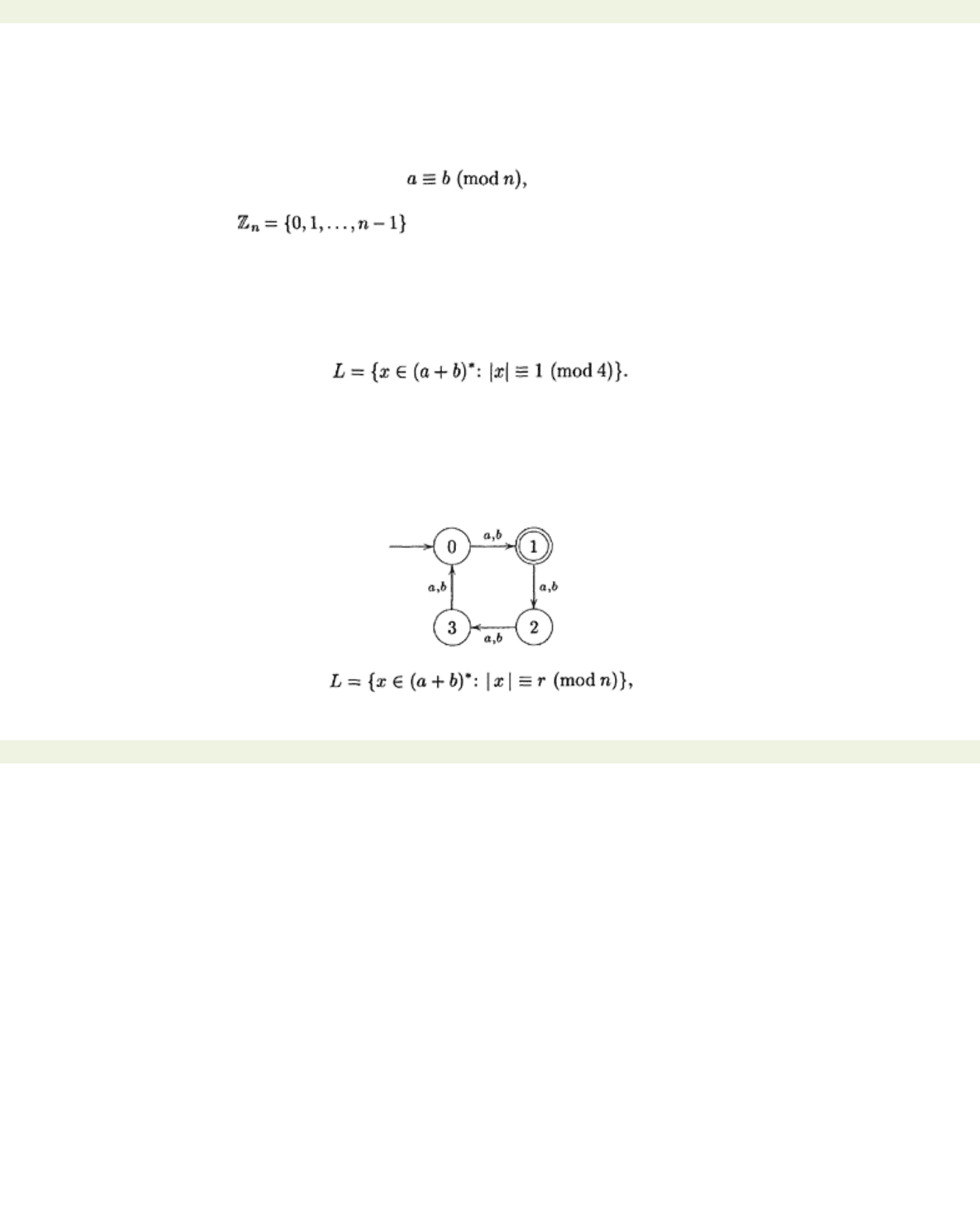
Example 2.3.2 Construct an automaton recognising the language
In this case, a string
x
is in
L
if its length is 1, 5, 9, 17,…. In other words, it has length one more than a
multiple of 4. Notice that we are not interested in the exact length of the string. It follows that we must
reject strings that have lengths 4
q,
4
q
+2, or 4
q
+3 for some
q
; we do not need to worry about strings
of length 4
q
+4 because that is itself a multiple of 4. In other words, there are only four possibilities,
and these four possibilities will be represented by four states in our machine. I will label them 0, 1, 2,
and 3, where the state
r
means ‘the length of the string read so far is 4
q
+
r
for some
q
.’ The automaton
that recognises
L
is therefore as follows:
It should now be clear that we can easily construct automata to recognise any language
L
of the form,
for any
n
≥2 and 0≤
r
<
n
. We now turn to a different kind of counting.
< previous page page_34 next page >

< previous page page_35 next page >
Page 35
Example 2.3.3 Construct an automaton which recognises the language
Here we are required to determine length up to some number; this is called ‘threshold counting.’ We
have to accept the empty string, all strings of length 1, and all strings of length 2; we reject all other
strings. We are therefore led to the following automaton:
In the above example, there is nothing sacrosanct about the number 3. Furthermore, we can easily
modify our machine to deal with similar but different conditions on |
x
| such as |
x
|≤3 or |
x
|=3 or |
x
|≥3
or where |
x
|>3.
Examples 2.3.1, 2.3.2, and 2.3.3 are typical of the way that counting is handled by automata: we can
determine length modulo a fixed number, and we can determine length relative to some fixed number.
Our next result shows that there are limits to what we can count using finite automata.
Proposition 2.3.4
The language
is not recognisable.
Proof When we say an automaton A recognises a language
L
we mean that it recognises
precisely
the
strings in
L
and no others.
We shall argue by contradiction. Suppose A=
(S, A, s0, δ, T)
is a finite automaton such that
L
=
L
(A). Let
where
n
≥0. Thus
qn
is the name we give the state that we reach when starting in the initial state
s
0
and inputting the string
an;
and
tn
is the name we give the state that we reach when starting in
qn
and
inputting
bn
. Then
s
0·
(anbn)
=
tn
and so
tn
is a terminal state because . We claim that if
i
≠
j
then
qi
≠
qj
. Suppose to the contrary that
qi
=
qj
for some
i
≠
j
. Then
But this would imply and we know
i
≠
j
. Since this cannot happen, we must have
i
≠
j
implies
qi
≠
qj
and so A has infinitely many states. This is a contradiction.
< previous page page_35 next page >

< previous page page_36 next page >
Page 36
The problem with the language
is that we have to compare the number of
a
’s with the
number of
b
’s and there can be an arbitrary number of both. Notice that we can construct an
automaton that recognises
a
*
b
*
:
Thus an automaton can check that all the
a
’s precede all the
b
’s.
The above result raises the following important question: how can we distinguish between recognisable
and non-recognisable languages? We shall investigate this question in Section 2.6.
Exercises 2.3
1. Let
A
=
{a, b}
. Construct finite automata for the following languages.
(i) All strings
x
in
A
* such that |
x
|=0 (mod 3).
(ii) All strings
x
in
A
* such that |
x
|=1 (mod 3).
(iii) All strings
x
in
A
* such that |
x
|=2 (mod 3).
(iv) All strings
x
in
A
* such that |
x
|=1 or 2 (mod 3).
2. Construct a finite automaton to recognise the language
3. Let
A
={0, 1}. Construct finite automata to recognise the following languages.
(i) All strings
x
in
A
* where |
x
|<4.
(ii) All strings
x
in
A
* where
|x
|≤4.
(iii) All strings
x
in
A
* where |
x
|=4.
(iv) All strings
x
in
A
* where |
x
|≥4.
(v) All strings
x
in
A
* where |
x
|>4.
(vi) All strings
x
in
A
* where |
x
|≠4.
(vii) All strings
x
in
A
* where 2≤|
x
|≤4.
< previous page page_36 next page >
