Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

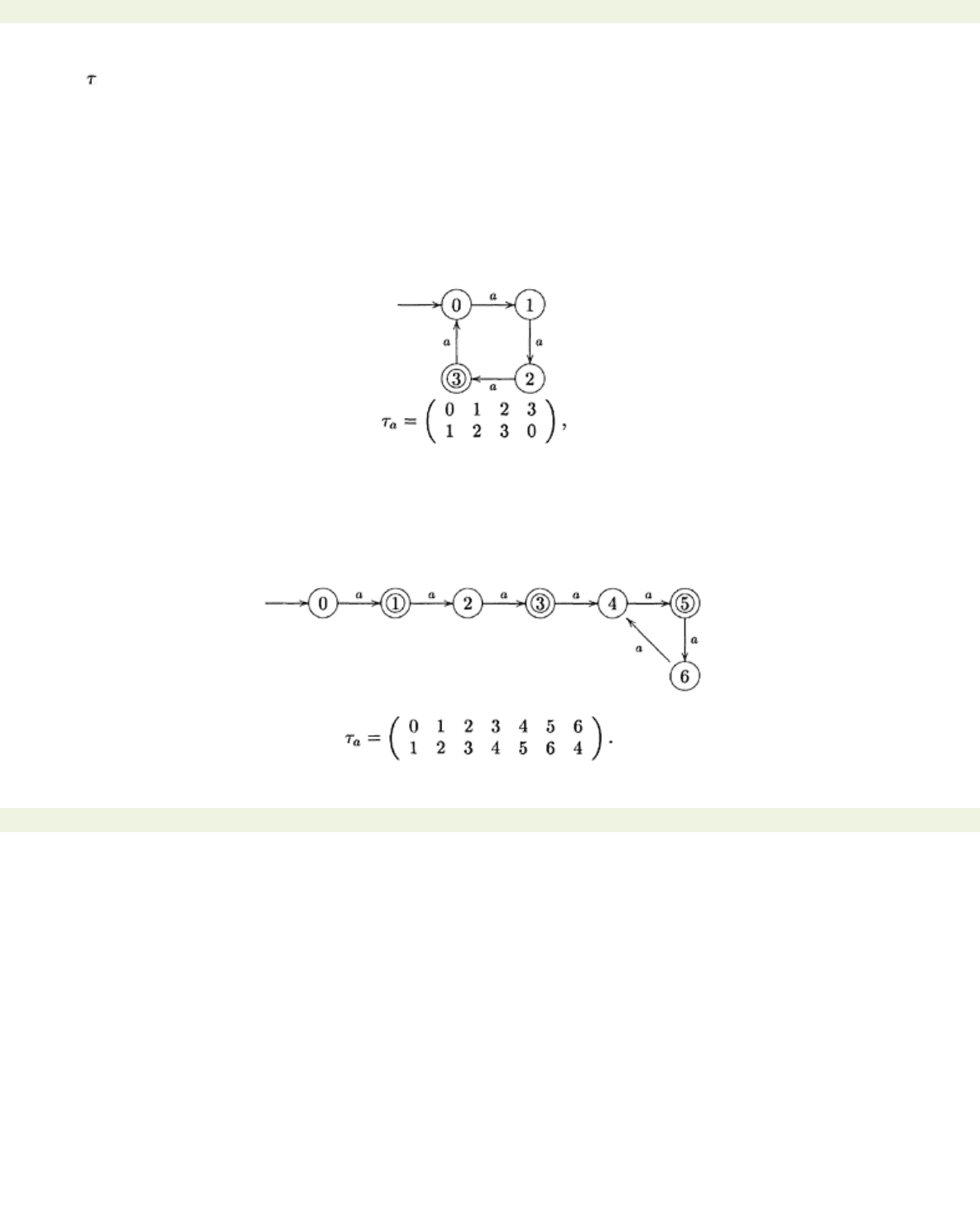
< previous page page_237 next page >

Page 237

where is the function defined in Section 8.1 that describes the effect of each input string on the set of

states.

Now suppose that

≥2, and concentrate first on the second summand. It is a union of languages of the

form

aq(ap)

all strings of

’s of length

modulo

. We assume that

the case where

≥

will be

treated in Example 11.1.4. We now look at the corresponding minimal automaton for this language. This

consists of

states arranged in a circle, numbered 0, 1,…,

−1, with the state 0 as the initial state and

the state

as the terminal state. The transition monoid of this automaton consists of all powers of the

function that maps

+1 for

=0, 1,…,

−2 and that maps

−1 to 0. This function has an additional

property: it is a bijective function on the set of states or, to use a more common term, a ‘permutation’

of the states.

Example 11.1.3 Consider the language

)

*. The minimal automaton for this language is

We have that

which is a permutation.

We now consider the case where

>1,

≥

and where there is also an

term. Then the transition

monoid again consists of all powers of a single function and this function combines features of both the

above cases. However, for

≥2 at least two of the states are permutated amongst themselves. This is

best illustrated by means of a concrete example.

Example 11.1.4 Consider the language

)

*. Its minimal automaton is

We have that

We see that the states {4, 5, 6} are permuted amongst themselves by this function.

< previous page page_237 next page >

< previous page page_238 next page >

Page 238

These examples lead us to formulate the following

conjecture:

over a one-letter alphabet, the star-free languages are characterised by the property that the transition

monoids of their minimal automata contain no element that induces a permutation on any subset of the

set of states containing at least two elements.

We shall prove that this conjecture is correct, and that it also holds for arbitrary alphabets.

Exercises 11.1

1. Construct the Cayley tables of the transition monoids in Examples 11.1.2, 11.1.3, and 11.1.4; use the

representation of elements by means of powers of

11.2 Groups

We begin with a definition that formalises the one we encountered informally in Section 11.1. A bijective

function in the full transformation monoid

T(X)

is called a

permutation

. We denote the set of

permutations in

T(X)

S(X);

the letter ‘S’ stands for ‘symmetry.’ If

={1,…,

} then we denote

S(X)

. When an element of

T(X)

is written in two-row form, it is easy to recognise when it represents a

permutation: the bottom row is simply the top row written in a different order. Our discussion in Section

11.1 has highlighted the importance of permutations in

T(X)

. There is another way of thinking about

them that we shall also need. Remember that, as usual, arguments of elements of

T(X)

are written on

the left.

Proposition 11.2.1

Let α: X

→

X be a function

Then α is a bijection if and only if there is a function β:

→

X such that αβ

βα, the identity function on X

Proof Let

β: X

→

be a function such that

αβ

βα

. We show that

is a bijection. Suppose that

xα

x′α

. Then

(xα)β

(x′α)β,

and so

x(αβ)

x′(αβ)

. But

αβ

is the identity function on

. Thus

x′,

and

is injective. Now suppose that . Then

y(βα)

because

βα

is the identity on

. Thus

(yβ)α

which shows that

is surjective. We have shown that

is a bijection.

Now suppose that

is a bijection. Let . Because

is a bijection there exists a unique element

such that

xα

. Define

yβ

. This is a well-defined function. By definition

y(βα)

which means

that

βα

. Suppose that

xα

. By definition

yβ

and so

x(αβ)

which means that

αβ

=1X.

< previous page page_238 next page >

< previous page page_239 next page >

Page 239

The characterisation of bijections we found above is the basis for the following abstract definition. Let

be a monoid with identity 1. An element is said to be

invertible

if there is an element such

that

The element

is called an

inverse

. Proposition 11.2.1 therefore shows that the invertible elements

T(X)

are precisely the permutations.

Lemma 11.2.2

Let S be a monoid.

(i)

If an element of a monoid has an inverse, then it has a unique inverse.

(ii)

If a and b are both invertible with inverses a′ and b′, respectively, then ab is invertible with inverse b

′a′.

Proof (i) Let

have inverses

and

b′

. Then 1=

and so

Hence

b′

(ii) It is enough to show that

which is straightforward.

Because of the above result we may speak of

the

inverse of an invertible element.

Notation We denote the inverse of the element

if it has one, by

−1. However, if the operation is

denoted by +, it is usual to denote the inverse by −

and the identity by 0 rather than 1. This has no

other basis than to make equations ‘look right.’

group

is a monoid in which every element is invertible. A

trivial group

is a group containing only the

identity element. The

order

of a finite group is simply the number of elements in the group. Let

be a

group and let

be a submonoid. We say that

is a

subgroup

if, in addition, for each

. It follows that

is a group in its own right. If

is a semigroup and

is a subsemigroup of

that is a group, then we say that

is a

group in S

Lemma 11.2.3

Let G be a group.

(i)

−1

)

−1=

g for each .

(ii)

If then .

< previous page page_239 next page >

< previous page page_240 next page >

Page 240

Proof (i) Simply observe that

−1 is

inverse of

and so it is

the

inverse of

by Lemma 11.2.2(i).

(ii) We use induction. The case

=2 is proved in Lemma 11.2.2(ii) and is our base case. Our induction

hypothesis is that the result is true for

. We prove it for

+1. Observe that

…gngn

)

−1=

((g

…

gn)gn

)

−1. This is equal to using the base case. The result now follows from the

induction hypothesis.

Denote the set of invertible elements in a monoid

U(S)

.1 Then

U(S)

is a group in

by Lemma

11.2.2(ii), called the

group of invertible elements of S

. A semigroup

is a group precisely when

U(S)

Examples 11.2.4 Here are some examples of groups of invertible elements.

(1) (

, +), ( , +) and ( , +) are all groups.

(2) ( , +) is a group. This is because for each there exists such that

=0 (mod

(3) The group of invertible elements in (

, ×) is { −1, 1}.

(4) The groups of invertible elements in (

, ×) and ( , ×) are and respectively.

(5) The group of invertible elements in

T(X)

S(X),

called the

symmetric group

Groups are special kinds of semigroups, and so we can look at homomorphisms between groups. These

have extra properties.

Lemma 11.2.5

Let α: G

→

H be a homomorphism between groups

Then α is a monoid homomorphism

and α(g

−1

)

α(g)

−1.

In particular, the image of α is a subgroup of H.

Proof We begin by showing that

is a monoid homomorphism. Denote both identities in

and

by 1.

We leave it as an exercise to prove that the only idempotent in a group is the identity. But

(1)2=

(1)

consequently

(1) is an idempotent and so is the identity of

Let . Then

−1=1=

−1

. Thus

α(g)α(g

−1

)

=1=

α(g

−1

)α(g)

. But these two equations imply that

α(g

−1

)

is the inverse of

α(g)

and so by the uniqueness of inverses we have that

α(g

−1

)

α(g)

−1.

We say that group homomorphisms ‘preserve inverses.’

We already know by Proposition 9.1.8, that the image of

is a submonoid of

. The fact that inverses

are preserved by a shows that the image of

1Invertible elements are sometimes called

units,

which explains the notation.

< previous page page_240 next page >

< previous page page_241 next page >

Page 241

actually a group and so a subgroup of

It follows that an

isomorphism of groups

is simply a bijective homomorphism.

Example 11.2.6 We have already noted that ( , +) is a group. We denote the set of positive real

numbers by

. It is an easy exercise to check that ( , ×) is a group. The (natural) logarithm function

is a homomorphism from ( , ×) to ( , +). This is because ln

(ab)

=ln

(a)

+ln

(b)

. There is an

inverse homomorphism

. Thus the two groups are isomorphic. This isomorphism is historically

important because it converts hard calculations involving multiplication into easy calculations involving

addition. For generations log-tables, and their mechanical analogues slide-rules, were the only tools

available for easing the burden of calculation.

Congruences can be defined on groups just as they can on arbitrary monoids. However, in the case of

groups congruences can be handled much more easily. We shall only need the result below, but see

Question 10 of Exercises 11.2 for the general result.

Proposition 11.2.7

Let θ

→

H be a homomorphism between groups. Put

Then K is a subgroup of G. Furthermore, it is trivial if and only if θ is injective.

Proof The subset

contains the identity of

because homomorphisms between groups are

automatically monoid homomorphisms by Lemma 11.2.5. Let . Then

θ(ab)

θ(a)θ(b)

=1. It

follows that

. Suppose that . Then

θ(a

−1

)

θ(a)

−1=1 by Lemma 11.2.5. It follows that

. Thus

is a subgroup of

. If

is injective, then clearly

will be trivial. We prove the

converse. Suppose that

is trivial and

θ(a)

θ(b)

. Then

θ(a)θ(b)

−1=1 and so

θ(ab

−1

)

=1. Thus

. By assumption

−1=1, from which it follows that

and so

is injective.

The result above tells us that to check whether or not a homomorphism between groups is injective, it

is enough to consider the inverse image of the identity: this is trivial if and only if the homomorphism is

injective.

Let

be a group. Then we can construct the monoid with respect to subset multiplication. In this

case we have an additional operation. If

is a subset of a group

define

Now define

< previous page page_241 next page >

< previous page page_242 next page >

Page 242

In a monoid

we defined

for . In a group

we define

−

−1

when

≥1. Thus in a

group

is defined for all .

Proposition 11.2.8

Let G be a group, and

Then X is a subgroup of G, the smallest subgroup

of G containing X.

If X={a}, then .

Proof Clearly

is a submonoid of

containing

. It is actually a subgroup of

by Lemma 11.2.3.

Clearly, any subgroup of

containing

must also contain

−1

and so it must contain . But a

subgroup is also a submonoid, and so a subgroup containing

must therefore also contain .

It follows that

is the smallest subgroup of

containing the set

To prove the final claim, note that any subgroup of

containing

must contain all the elements

where . But the set is also a subgroup of

. The result now follows.

Let

be a group. For we call

the subgroup of

G generated by X

. A group

is said to be

cyclic if for

some .

Notation It is important to remember that for

≥1 the notation

means ‘

composed with itself

times using the group operation.’ Thus if the group operation is denoted by +, we usually write

rather than

an,

where

means ‘

added to itself

times.’ If

<0 then

means

(−n)(−a)

where we

use −

to denote the inverse of

Examples 11.2.9 We so far have two classes of examples of cyclic groups.

(1) The group ( , +) is an infinite cyclic group. The elements of 1 are of the form

where

, and so the result is clear.

(2) For

>1 the group ( , +) is cyclic of order

. The elements of 1 contain

for

≥0 modulo

and so will contain all elements of .

The following theorem shows that the examples (1) and (2) above constitute a complete list of all cyclic

groups.

Theorem 11.2.10

Each infinite cyclic group is isomorphic to

( , +)

and each finite cyclic group is

isomorphic to

( , +)

for some n

Proof Let

be a cyclic group. Then

for some . Observe first that if two distinct powers of

are equal then

must be finite. For suppose

< previous page page_242 next page >

< previous page page_243 next page >

Page 243

that

for some

. Then 1=

−

. By taking inverses of both sides of this equation if necessary, it

follows that there is a positive integer

such that

=1. Choose

>0 as small as possible such that

=1. Let be arbitrary. Then

where 0≤

by the Remainder Theorem. But then

Thus

It follows that

and so

is finite.

Suppose that

is infinite. Then by the above result distinct powers of

are distinct. Therefore the

function given by

α(ai)

is well-defined. It is immediate that

is a bijection. It is a

homomorphism because

We have shown that

is isomorphic to under addition.

Now suppose that

is finite. Then not all powers of

can be distinct. Let

be the smallest positive

integer such that

=1. Then

,…, an

−1

}

by our result above. We prove that

is isomorphic to (

, +). Define by

α(ai)

. This is clearly a bijection. It is a homomorphism because

aiaj

and

where and

(mod

). But in ( , +), we have that

. Thus

isomorphic to (

, +).

Let

be a semigroup, and let be an idempotent. It is easy to check that

is a subsemigroup of

which is also a monoid in its own right with identity

. We call

eSe

local

monoid in S

Proposition 11.2.11

Let S be a semigroup.

(i)

For each idempotent e in S, the group U(eSe)

He, the containing the idempotent e

(ii)

Let G be a group in S with identity e. Then .

Proof (i) Let . Then there exists such that

. Now

and

imply that

, and

and

imply that . It follows that .

Now let . We prove that . By definition there exist such that

< previous page page_243 next page >

< previous page page_244 next page >

Page 244

First,

Thus

. Observe that

and

Put

u′

eue

and

x′

exe

. Then

Thus

u′a

au′

and and so .

(ii) If then

since e is the identity of

. Thus

ege

. It follows that . The next

assertion is immediate because each element of

is invertible in

eSe

The following definition now makes sense. Let

be a semigroup and let be an idempotent. Then

the group

U(eSe)

is called a

maximal group in S around the idempotent e

Example 11.2.12 Let be the monoid of 2×2-matrices under multiplication with entries from

. The identity of this monoid is the 2×2 identity matrix, and the zero is the 2×2 zero matrix. The

matrix,

is an idempotent that is neither the identity nor the zero. The subsemigroup

eSe

consists of all matrices

of the form,

where , whereas

U(eSe)

consists of all such matrices where

≠0.

Lemma 11.2.13

Let α: S

→

T be a semigroup homomorphism

(i)

If e is an idempotent in S then α(e) is an idempotent in T.

(ii)

If α is restricted to eSe then the image is contained in α(e)Tα(e).

(iii)

If a is restricted to Hethen the image is contained in Hα(e).

< previous page page_244 next page >

< previous page page_245 next page >

Page 245

Proof (i) Let

be an idempotent in

. Then

α(e)

α(e

)

α(e)

2. Thus

α(e)

is an idempotent in

(ii) Let

. Then

and so

which implies that .

(iii) Let . By (ii) above, we have that . By assumption, there exists such

that

and so

α(a)α(b)

α(e)

α(b)α(a),

and so

α(a)

is invertible in the monoid

α(e)Tα(e)

with

inverse

α(b)

. Hence .

In general,

eSe

is not itself a group. However, it is useful to have a criterion when it is.

Proposition 11.2.14

Let S be a semigroup and let e be an idempotent in S. Then eSe is a group if and

only if the following property holds: if I is any non-empty left ideal and

then I

Proof Let

eSe

be a group. Suppose that is a non-empty left ideal. Let . Then .

Thus

for some . It follows that . Put

. Thus because

is a left

ideal, and by construction. By assumption

eSe

is a group. So there exists such that

Thus because

is a left ideal. It follows that and so

as required.

To prove the converse, assume that

contains no proper non-empty left ideals. We prove that

eSe

a group. Let

. Then

. It follows that . But

is a non-empty left ideal.

Thus by assumption

. It follows that there exists such that

. But

(ebe)a

. Put

′

ebe

. Then and

b′a

. Now . Thus

b′

. It follows that there exists

such that

db′

. But

(ede)b′

. Put

d′

ede

. Then and

d′b′

. We therefore have that

(d′b′)a

d′(b′a)

d′e

d′

. Therefore

b′a

ab′

and so . It follows that

eSe

U(eSe)

Let

be an idempotent in a semigroup

. We say that

is a

minimal left ideal

where

is a

non-empty left ideal, implies that

. Thus the above result tells us that

eSe

is a group precisely

when

is a minimal left ideal.

To finish off this section we shall look at two important examples of groups in semigroups: groups in

transition monoids and groups in Schützenberger products.

We usually present the syntactic monoid as a submonoid of the full transformation monoid on the set of

states, so it is useful to know how groups in transition monoids can be identified. The following

proposition gives us some information; the important result is (iii) below.

< previous page page_245 next page >

< previous page page_246 next page >

Page 246

Proposition 11.2.15

Let S be a submonoid of a full transformation monoid T(X) where X is a finite set.

(i)

Let G be a non-trivial group in S. Then there exists a subset such that the restrictions of the

elements in G to Y are permutations that form a group isomorphic to G.

(ii)

Suppose there exists a subset and an element such that s restricted to Y is a non-

trivial permutation. Let H be the subgroup of S(Y) generated by all such permutations. Then there is a

group G in S such that H is a homomorphic image of G.

(iii)

The monoid S contains a non-trivial group if and only if there is an element and a subset Y of

X with at least two elements such that s induces a non-trivial permutation on Y.

Proof In this proof, remember that elements of

are functions that have arguments written on the left,

so that if and then .

(i) By Proposition 11.2.11, for some idempotent . Put

Xe,

the image of

under the

function

. For each define the function

as follows: its domain is

its codomain is

and for

each we define

yfa

. The function

will be well-defined if we show that its codomain really is

but this is true because for each we have that

Put

Observe that

is the identity function on

because if there exists such that

and so

The function

is a bijection of

because there is an element such that

. Observe that

fafb

fab

for all . It follows that

is a subgroup of

S(Y).

Define a function from

. It is immediate that it is a homomorphism. We prove that it is a bijection. By construction it is

surjective, so we need only prove that it is injective. Let be such that

. Then

yfa

yfb

for

all . Let be arbitrary. Then

x(ea)

(xe)fa,

where . Similarly

(xe)fb

. But

(xe)fa

(xe)fb

by assumption, and so

for all . It follows that

as required.

(ii) Let

be the subset of

consisting of all those elements that induce a permutation of

. By

assumption, this set contains more than just the identity function. It is evident that

is closed under

composition of functions and so is a submonoid of

. Because

is finite it contains idempotents by

< previous page page_246 next page >