Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_217 next page >

Page 217

Chapter 10

Algebraic language theory

In Chapter 9, we proved that a language is recognisable precisely when its syntactic monoid is finite.

When the language is recognisable, the syntactic monoid can easily by calculated as the transition

monoid of the minimal automaton of the language. The goal of algebraic language theory is to answer

questions about recognisable languages by studying their syntactic monoids. To do this, we first have to

learn more about finite semigroups. This is the subject of Section 10.1. To demonstrate that the

algebraic approach is viable, we show in Section 10.2 that many of the results about recognisable

languages proved in Chapters 3 and 4 using automata can easily be proved using finite monoids. The

real vindication of this approach, however, will come in Chapter 11, when we prove a new result about

recognisable languages using the syntactic monoid. The results of this chapter lead us to look for a

correspondence between recognisable languages and finite monoids. In Section 10.3, we prove that this

correspondence cannot be interpreted in a naive way. The correct correspondence is described in

Chapter 12.

10.1 Finite semigroups

An element

of a semigroup is said to be

idempotent

. Zero elements and identities are

idempotents, but there are idempotents that are neither.

Example 10.1.1 Let

be any non-empty finite set with

elements. Define a binary operation on

for all . Then

is a semigroup. For

≥2, every element of

is idempotent but none

is an identity nor a zero.

The following result is a direct consequence of finiteness.

Theorem 10.1.2

Every element in a finite semigroup has a non-zero power that is idempotent, and so

every finite semigroup contains an idempotent.

< previous page page_217 next page >

< previous page page_218 next page >

Page 218

Proof Let

be a semigroup with

elements and let . Consider the list

s, s

,…, sn

+1. Because

contains

elements, there must exist at least two powers of

say

and

sj,

where

such that

Let

for some

≥1, so that

sisk

. Now

sisk

sisksk

. By induction,

for all

≥0. The numbers

i, i

+1,…

−1) are

consecutive numbers. A little thought will convince you

that these numbers must each be congruent modulo

to exactly one of the numbers 0, 1,…,

− 1 in

some order. Let

be in the range 0≤

≤

−1 such that

=0 (mod

). Then

for some

. The

element

is idempotent because

A finite semigroup might well have neither identity nor zero, but it will always have idempotents.

Finiteness is essential in the above theorem. For example, the infinite semigroup

+ does not have any

idempotents.

Amongst the subsemigroups of a semigroup, there are some with a stronger property. Let

be a

semigroup. A subset

is said to be a

right ideal

left ideal

and a

two-sided

ideal

if it is ambidextrous. An ideal (left, right two-sided)

is said to be

proper

if it is not equal to

then

, S

and

1 are, respectively, the smallest right, the smallest left, and the

smallest two-sided ideals containing

.1 Ideals arise in the following way. In ordinary arithmetic, we are

often interested in whether one number divides another. For example, we define even numbers to be

those divisible by 2 and prime numbers as those numbers (apart from 0 and 1) having the smallest

possible number of divisors: namely, 1 and themselves. We can similarly talk about divisibility in

semigroups. However, we come up against an important difference: in general, the multiplication in a

semigroup is not commutative. For that reason, we have to study three different kinds of divisibility. In

the definition below, is just a way of saying that either

or . Let

be a semigroup,

and let . If

then we write

≤

. If

≤

and

≠

then we write

. If

≤

and

≤

Ra,

then we write . We may dually define ≤

and . Define

≤

if . We define <

and in the obvious ways. Finally, put . When

is a monoid, we can clearly use

itself

rather than

1 in the definitions above.

Example 10.1.3 Consider the monoid

*. Then

≤

means precisely that

is a prefix of

x; x

means that

is a proper prefix of

. In this case, is the equality relation (why?). By the same token,

≤

means that

is a suffix of

and

≤

J y

means that

is a factor of

1The curious terminology ‘ideal’ goes back to their origins in ring theory. See [46].

< previous page page_218 next page >

< previous page page_219 next page >

Page 219

The proof of the following is left as an exercise.

Lemma 10.1.4

Each of the relations ≤R, ≤L and ≤J is reflexive and transitive.

Relations that are both reflexive and transitive are called

preorders

. Such relations have the following

important properties.

Lemma 10.1.5

Let

be a preorder on the set X. Define x

y iff and

. Then

is an

equivalence relation on X

Denote by X

the set of equivalence classes and [x] the equivalence class containing x

Define [x]

≤

[y]

iff

Then

≤

is a partial order on X

/=.

Proof It is easy to check that = is an equivalence relation. We show that ≤ is well-defined. Let

and . Then and so by transitivity. It is left as an exercise to check that ≤ is

a partial order.

It follows from Lemmas 10.1.4 and 10.1.5 that

and are equivalence relations on any semigroup

. The relation , which is the intersection of two equivalence relations, is itself an equivalence relation

(by Question 3 of Exercises 7.1). They are called

Green’s relations

. Observe that . This means

that each is a union of some of the and some of the (again by Question 3 of

Exercises 7.1). In addition, is a partially ordered set by Lemma 10.1.5. There is one piece of

idiosyncratic notation concerning Green’s relations that is common in semigroup books. If is any one

of Green’s relation, then the containing the element

is denoted

Theorem 10.1.6

Let S be a finite semigroup. The following are equivalent.

(i) .

(ii)

for some

(iii)

for some

Proof (i)

(ii). Suppose that . Then by definition,

for some . Notice that

It follows that

(ux)ma(yv)m

for all

≥1. Similarly

(xu)mb(vy)m

. Because

is finite there is a

positive integer

such that

(ux)p

an idempotent by Theorem 10.1.2. We have that

ea(yv)p

and

< previous page page_219 next page >

< previous page page_220 next page >

Page 220

It follows that

((ux)p

−1

u)xa

. Hence . Similarly, there is a positive integer

such that

(vy)q

is an idempotent. Now

by simply rewriting

x(ux)q

+1 and

(yv)q

+1. But

because

(vy)q

is an idempotent. But then,

Thus

(vy)q

−1

. But we also have

so we have proved that .

(ii)

(iii). The proof of this implication does not require finiteness. Suppose that for some

. By definition there are such that

Put

ycu.

We prove that and . To prove the first equivalence,

and

To prove the second equivalence,

and

(iii) (i). Straightforward.

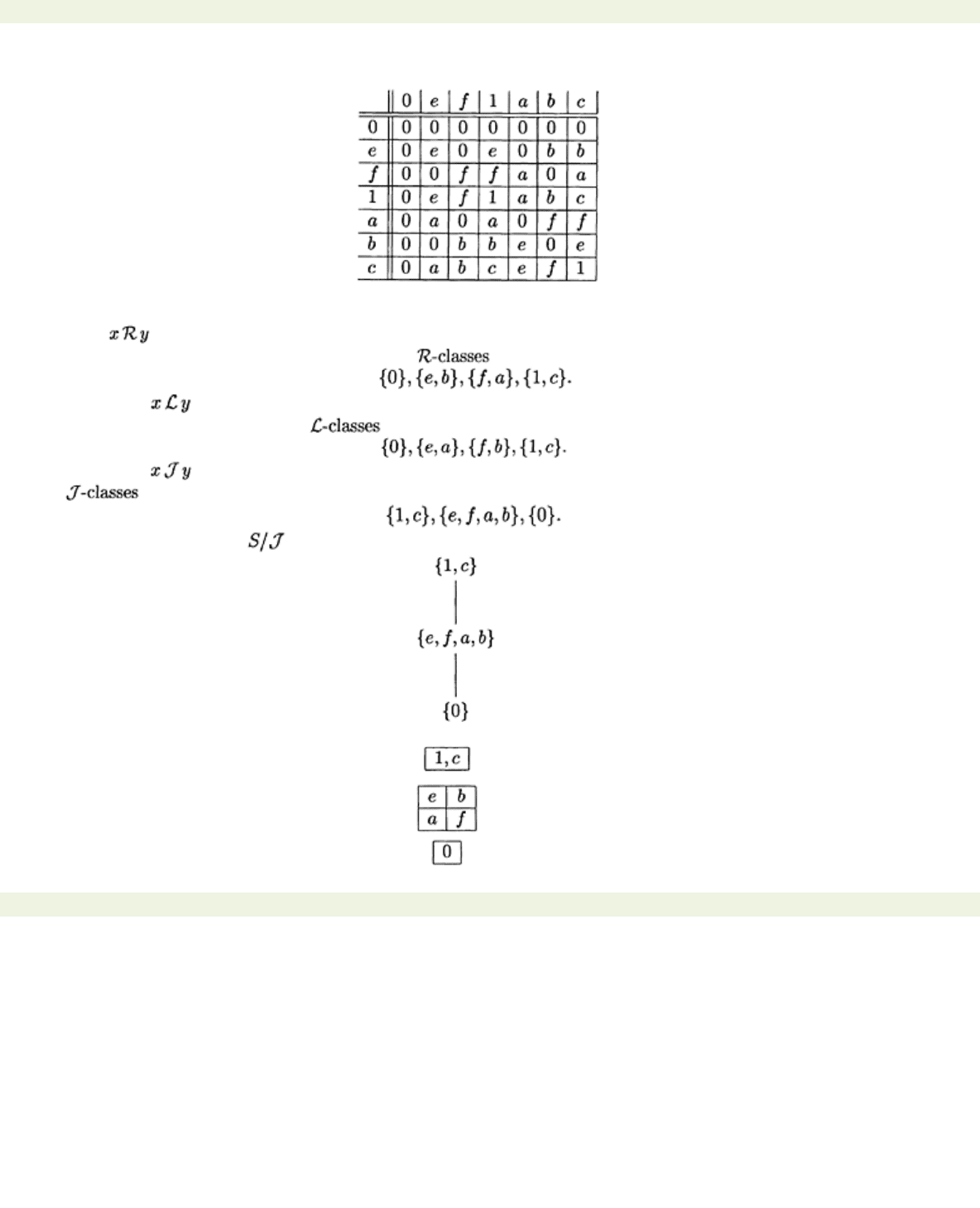
The result above is the basis of a pictorial device for representing the divisibility properties of finite

semigroups. I shall describe how this is constructed in stages. First, draw the Hasse diagram of the

partially ordered set . Next each vertex of the diagram is replaced by the corresponding .

Then each is divided into rows, where each row is an class. Finally, each is

divided into columns, where each column is an . Theorem 10.1.6 tells us that each row and each

column in a intersect in an . The resulting diagram is called an

eggbox diagram

< previous page page_220 next page >

< previous page page_221 next page >

Page 221

Example 10.1.7 What follows is the Cayley table of a monoid

We shall calculate Green’s relations for this monoid, and display them by means of an eggbox diagram.

Observe that because

is a monoid, Green’s relations can be defined in terms of

rather than

1. To

calculate we have to show that

. The set

is simply the set of elements occurring in the

row of the Cayley table belonging to

. The are therefore:

To show that

we have to show that

. The set

is simply the set of elements occurring in

the column belonging to

. The are therefore:

To show that have to show that

SxS

SyS

. We can use our previous calculations since

SxS

The

are therefore:

The partially ordered set can therefore be represented by the following Hasse diagram:

The eggbox diagram is therefore:

< previous page page_221 next page >

< previous page page_222 next page >

Page 222

There is an important technique for combining semigroups to make new ones. Let (

) and (

*) be

semigroups. On the set

define a binary operation as follows: if

then

Define functions

, π

: S

→

(s, t)

and

(s, t)

. The proof of the following is left as an

exercise.

Lemma 10.1.8

With the definition above, if S and T are semigroups, then S

T is a semigroup, and

and π

are semigroup homomorphisms. If S and T are both monoids, then S

T is a monoid, and

and π

are monoid homomorphisms

The construction above can be generalised as follows. Let

be semigroups (respectively monoids). Then

is a semigroup (respectively monoid) under

pointwise

multiplication: the product of

,…, an)

and

…, bn)

is defined to be

,…, anbn)

. The function,

where 1≤

≤

is a homomorphism (respectively, monoid homomorphism), called the ith

projection

homomorphism

. The semigroup

1×

…

is called the

product

of the semigroups

. We shall

sometimes write this product as . An element of is an

-tuple, which we shall write as

(si),

where 1≤

≤

Example 10.1.9 Let

, S

3 be three semigroups. We can first form the product

1×

2 and then

we can form the product

1×

)

3. Similarly, we can form the product

1×

2×

)

. The semigroups

1×

)

3 and

1×

2×

)

are isomorphic where the isomorphism takes

((s

, s

), s

)

, (s

))

. We leave the simple verification as an exercise. It is also easy to check that both

1×

)

3 and

1×

2×

)

are isomorphic to

1×

2×

3. This result can be generalied to deal with any product of

semigroups.

The following combines subsemigroups, products, and homomorphic images and is left as an exercise.

< previous page page_222 next page >

< previous page page_223 next page >

Page 223

Lemma 10.1.10

Let S

,…, Snand T

,…, Tnbe semigroups

(i)

Let Si be a subsemigroup of Ti for each

1≤

≤

Then S

1×

…

Snis a subsemigroup of T

1×

…

(ii)

Let αi: Si

→

Ti be a homomorphism for each

1≤

≤

Then

defined by

is a homomorphism.

Exercises 10.1

1. Let

be a set with

elements and product defined by

. Show that

is a semigroup in which

every element is idempotent.

2. Show that

is an idempotent in

if and only if

restricted to im

(α)

is the identity function.

3. Prove Lemma 10.1.4.

4. Complete the proof of Lemma 10.1.5.

5. Show that in a commutative semigroup .

6. Let

and

be idempotents in a semigroup

. Prove that

(i)

and

(ii)

and

7. Let

be a finite, non-empty set. Show that in the full transformation monoid

T(X)

the following hold:

(i) .

(ii) .

(iii) .

Hence construct the eggbox diagrams of

2 and

8. Prove Lemma 10.1.8.

< previous page page_223 next page >

< previous page page_224 next page >

Page 224

9. Let

, S

3 be semigroups. Prove that

1×

2×

)

is isomorphic to

1×

)

10. Prove Lemma 10.1.10.

10.2 Recognisability by a monoid

The syntactic monoid of a recognisable language can be constructed from the minimal automaton of the

language. But just as languages can be recognised by automata that are not minimal so they can also

be recognised by monoids that are not their syntactic monoids. To make this precise we need to

develop a little more semigroup theory.

Theorem 10.2.1

Let A be a finite alphabet.

(i)

Let S be a semigroup and let α: A

→

S be a function

Then there is a unique homomorphism

such that

for each .

(ii)

Let S be a monoid and let α: A

→

S be a function

Then there is a unique monoid homomorphism

such that for each .

Proof We prove (i), and then the proof of (ii) is immediate. Let . Define

It is easy to check that is a homomorphism, and by construction it has the correct property.

The above theorem has an important consequence.

Proposition 10.2.2

(i)

Let S be a finitely generated semigroup. Then S is a homomorphic image of A

for some finite

alphabet A

(ii)

Let S be a finitely generated monoid. Then S is a monoid homomorphic image of A

for some finite

alphabet A

Proof We prove the semigroup case. The monoid case is then immediate. Since

is a finitely generated

semigroup, there is a finite subset

such that

+. Let

be any set that has the same number

of elements as

. This means that there is a bijection from

. Thus each element of

corresponds

to a unique element of

. By Theorem 10.2.1, there is a homomorphism

from

+ to

which maps

each element of

to the corresponding element of

. By Proposition 9.1.8, the image of

is a

subsemigroup of

< previous page page_224 next page >

< previous page page_225 next page >

Page 225

containing

. Thus the image of

contains

. Hence

is surjective.

Because of Proposition 10.2.2, the semigroups

+ and the monoids

* play a special role in the theory

of semigroups. Loosely speaking, they form the templates from which all (finitely generated) semigroups

and monoids can be built by means of homomorphic images.

Let

be a finite alphabet. The semigroup

+ is called the

free semigroup on the set A

because of the

property described in Theorem 10.2.1. Similarly, we say that

* is the

free monoid on the set A

There is a further consequence of Theorem 10.2.1, which we shall use later in this chapter.

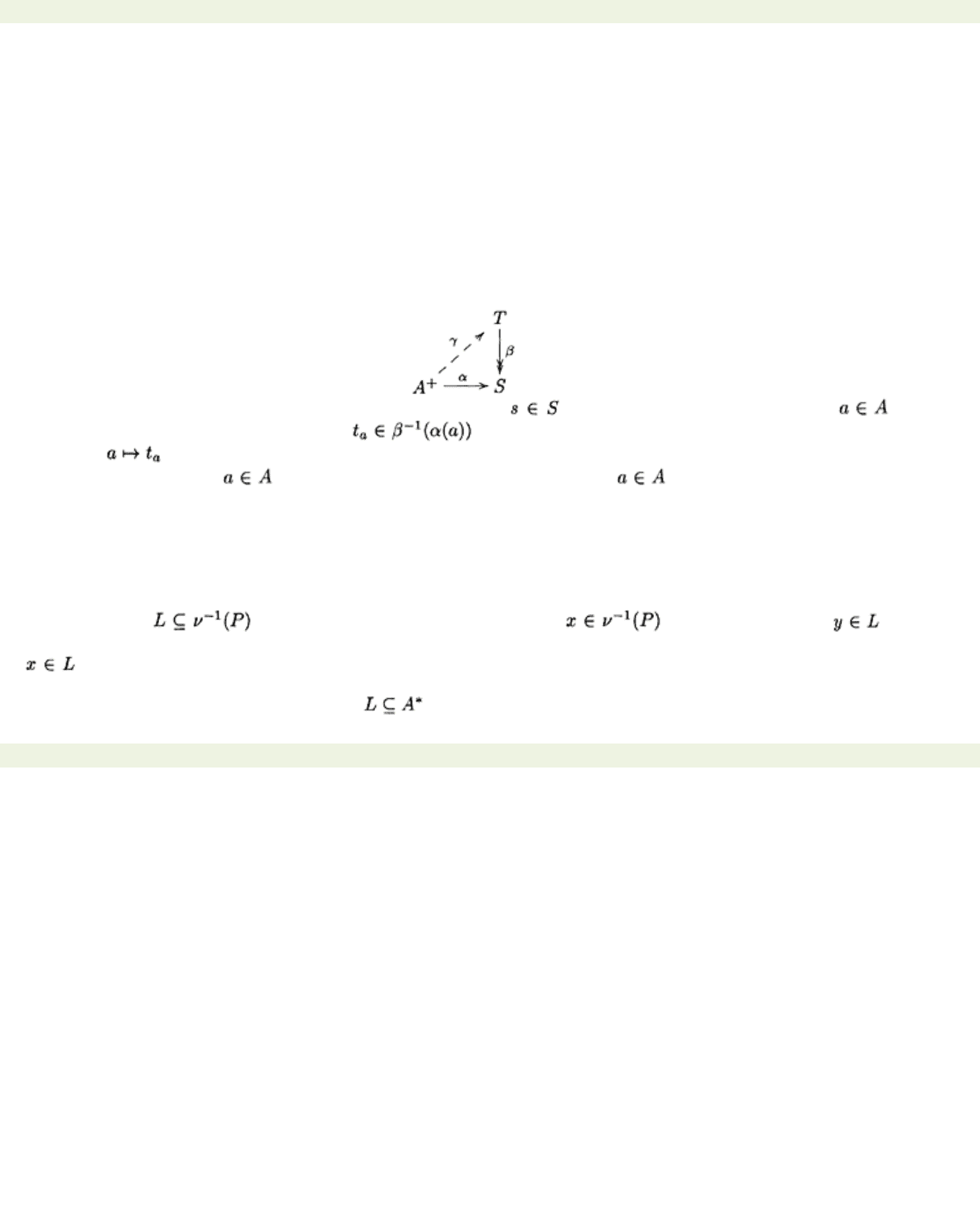
Proposition 10.2.3

Let α: A

+→

S be a homomorphism, and let β: T

→

S be a surjective homomorphism

Then there is a homomorphism γ: A

+→

T such that βγ

The same result holds when A

is replaced by

and all the homomorphisms are monoid homomorphisms

Proof In the diagram below, the solid arrows represent the homomorphisms we have been given and

the dashed arrow is the one we have to define.

Because

is surjective,

−1

(s)

is non-empty for each the set. In particular, for each the

set

−1

(α(a))

is non-empty. Choose . We have therefore defined a function from

given by . By Theorem 10.2.1, this can be extended to a unique homomorphism

γ: A

+→

such

that

γ(a)

for each . It follows that

β(γ(a))

α(a)

for each . Thus the homomorphisms

βγ

and

agree on the generating set

and so they must agree on the whole of

+. It follows that

βγ

α,

as required.

To motivate what follows, we isolate an important property of the syntactic monoid of a language.

Lemma 10.2.4

Let L be a language over the alphabet A, let M(L) be its syntactic monoid, and let ν:

*→

M(L) be the homomorphism that maps a string x to σL(x)

Let P

ν(L), a subset of the syntactic

monoid

Then L

−1

(P)

(ν

−1

ν)(L)

Proof Clearly

. We prove that equality holds. Let . Then there exists such

that

ν(x)

ν(y)

and so

xσLy

. But by Proposition 9.4.2, the language

is a union of

σL

-classes. Thus

as required.

The result above motivates the following definition. Let

be a finite alphabet,

a monoid, and

α:

*→

a monoid homomorphism. Let .

< previous page page_225 next page >

< previous page page_226 next page >

Page 226

We say that

α recognises L

if there is a subset such that

−1

(P)

. Usually, we shall just say

that the monoid

itself

recognises

the language

. In particular, the syntactic monoid

M(L)

recognises

by Lemma 10.2.4. We say that a language

recognisable (by a monoid)

if it is recognised by a

finite

monoid. Our first task is to show that this new type of recognisability agrees with our usual definition

via automata.

Theorem 10.2.5

A language is recognisable by a monoid if and only if it is recognisable in the

automata-theoretic sense.

Proof Let A=

(Q, A, i, δ, T)

be an automaton such that

(A)=

and let

(A) be the transition monoid

of A. Denote by the function associating a string with the effect of the string on the set of

states

. Thus . Put

the image of the language in the transition monoid. Clearly

. We show that in fact equality holds. Let . Then by definition there exists

such that . But and so because

and

have the same effect on the

states of A. Hence as required.

To prove the converse, suppose that

is recognised by a finite monoid. Specifically, there is a monoid

homomorphism

α: A

*→

and a subset such that

−1

(P)

. We shall prove that

is recognised

by a finite automaton. Define A=(

M, A,

δ, P

)

where 1 is the identity of

and

δ(m, a)

mα(a)

. It is

clear that A is a finite automaton. If

is a string in

* then

(m, u)

mα(u)

. We now determine

(A).

We have that iff iff . Hence

(A)=

A regular language may be recognised by many different monoids. The syntactic monoid occupies a

privileged position that can be characterised using a definition combining subsemigroups with

homomorphic images. Let

and

be semigroups. We say that

N divides M

is a homomorphic

image of a subsemigroup of

that is, there is a subsemigroup and a surjective homomorphism

α: M′

→

. If

and

are both monoids, we say that

divides

is a monoid homomorphic image

of a submonoid of

Theorem 10.2.6

Let L be a language over the alphabet A. The monoid M recognises L if and only if

M(L) divides M where M(L) is the syntactic monoid of L.

Proof Suppose that

is a monoid that recognises

. Then by definition there is a monoid

homomorphism

α: A

*→

and a subset such that

−1

(B)

. We show first that . Let

α(x)

α(y)

and suppose that for some . Then and so

which

implies that

. A similar argument shows that implies that . We have therefore

proved that implies . Let

M′=

(α)

. By Proposition 9.2.12, there is a surjective

homomorphism from

M′

M(L)

. It follows that

M(L)

divides

as required.

< previous page page_226 next page >