Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_197 next page >

Page 197

To check that a function is an isomorphism involves three things: showing that it is a homomorphism,

showing that is it a bijection, and showing that its inverse is a homomorphism. In fact, the last

condition comes for free.

Proposition 9.1.11

A bijective homomorphism is an isomorphism.

Proof Let

α: S

→

be a bijective homomorphism. We prove that

−1 is a homomorphism, which justifies

the claim. Let

Put

−1

(t)

and

s′

−1

(t′)

. Because

is a homomorphism

α(ss′)

α(s)α(s′)

Thus

ss′

−1

(α(s)α(s′))

. We therefore have

−1

(t)α

−1

(t′)

−1

(tt′)

and so

as required.

Exercises 9.1

1. Let

be a semigroup. Show explicitly that

for all

2. Let be the set of all real numbers. Show that the operation of subtraction is a binary operation on

but that it is neither associative nor commutative.

3. Let

be the set of all positive real numbers. Let ÷ denote the operation of division in which

. Show that ÷ is a binary operation on that is neither associative nor commutative.

4. Consider the operation

on , defined by the rule: . Show that ( , ) is a

commutative monoid.

5. Let denote the binary operation on defined . Show that is both commutative

and associative so that (

, ) is a commutative semigroup. Is ( , ) a monoid?

6. Let

. Show that

is a submonoid of with respect to addition. Find an explicit

description of the elements of

in particular what is the largest element of not in

Subsemigroups of

( , +)

are called

numerical semigroups.

You can find out more about them in [48],

for example.

7. Let

be the following element of

< previous page page_197 next page >

< previous page page_198 next page >

Page 198

Find all the elements in

8. Let

be the set of 2×2-matrices with coefficients from . Show explicitly that

is a monoid. Let

the monoid ( , ×). Define

δ: S

→

δ(A)

−

where

Show that

is a monoid homomorphism.

9. Complete the proof of Proposition 9.1.8.

10. Let

S, T

and

be semigroups. Prove the following:

(i) The identity function on

is an isomorphism from

to itself.

(ii) If

θ: S

→

is an isomorphism then

−1

: T

→

is an isomorphism.

(iii) If

θ: S

→

and are both isomorphisms then is an isomorphism.

11. Let

and

be isomorphic semigroups.

(i) Prove that |

iff |

(ii) Prove that

has an identity if and only if

has an identity.

(iii) Prove that

has a zero if and only if

has a zero.

(iv) Prove that

is commutative iff

is commutative.

9.2 Congruences

In Section 7.1, we showed that partitions and equivalence relations were different ways of thinking

about the same thing. We now introduce another way of thinking about equivalence relations that is

important in algebra.

Lemma 9.2.1

Let α: X

→

Y be a function between two sets

The set,

consisting of the inverse images of each of the elements in the image of α, is a partition of X.

Proof Each

−1

(y)

is non-empty, because

is chosen from the image of

. Suppose that

. Then there exists . But then

α(x)

and

α(x)

y′

. But

is a

function and so

y′,

which implies that

−1

(y)

−1

(y′)

. Finally, if then

α(x)

for some .

Hence

. We have shown that the three defining conditions

< previous page page_198 next page >

< previous page page_199 next page >

Page 199

for a partition of Section 7.1 hold.

The following example illustrates this result.

Example 9.2.2 Consider the function

→

where

and where the rule is given by means of the table below:

Notice that

is not surjective, because

is not in the image of

. The partition

induces on

We know from Section 7.1 that partitions and equivalence relations contain exactly the same

information. We can easily write down the equivalence relation associated with a function via its

partition: this relation is just

The relation ~ is usually denoted by ker

(α)

and is called the

kernel of α

Thus each function gives rise to an equivalence relation on its domain. On the other hand, the next

result tells us that we can construct surjective functions from equivalence relations.

Lemma 9.2.3

Let ρ be an equivalence relation on the set X. Define

by mapping x to ρ(x), the ρ-equivalence class that contains x. Then v is a surjective function.

Proof The equivalence relation

induces a partition on the set

whose blocks are the

-equivalence

classes. Each element of

belongs to a unique equivalence class, so that

is a well-defined function,

and because equivalence classes are non-empty, the function

is surjective.

The function

is called the

natural function

associated with the equivalence relation

and is sometimes

written

If we start with a function, we can construct an equivalence relation, and from that equivalence relation

we can construct its natural function. We are impelled to ask how the original function and the natural

function are related

< previous page page_199 next page >

< previous page page_200 next page >

Page 200

to each other. The following theorem answers this question.

Notation It is common to represent surjective functions thus:

and injective functions so:

Functions whose existence we assume are usually represented using solid lines, whereas functions

whose existence we are trying to establish are often represented using dashed lines. We shall use these

conventions whenever they help clarity.

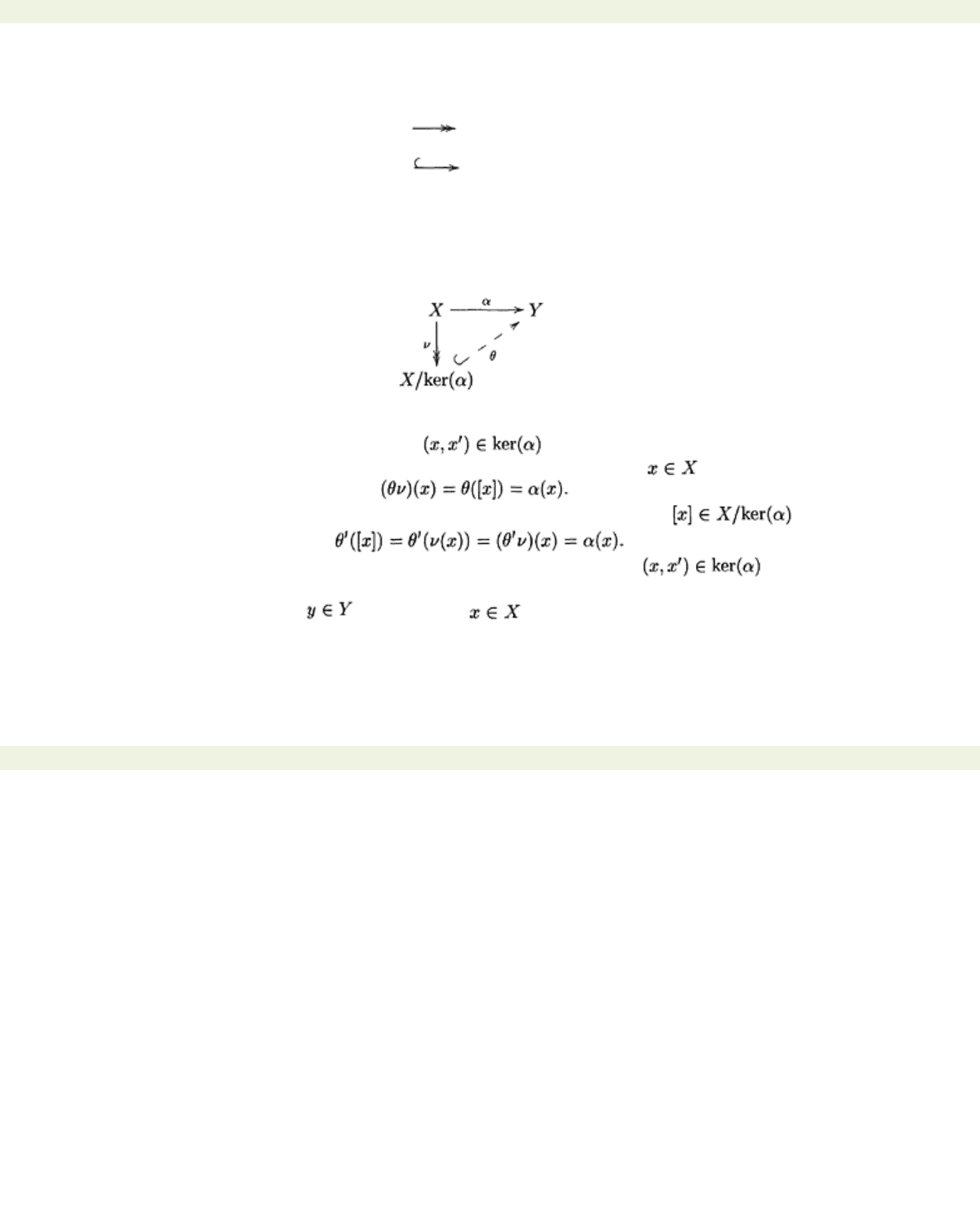
Theorem 9.2.4

Let α: X

→

Y be a function

Let ν: X

→

/ker

(α) be the natural function associated with

the equivalence relation

ker

(α)

Then there is a unique function θ: X

/ker

(α)

→

Y such that θν

addition, θ is injective.

The function θ is surjective if and only if α is surjective.

Proof Denote the ker

(α)

-equivalence class containing

[x]

. Define

to map

[x]

α(x)

. To see this

is well-defined, suppose that

[x]

[x′]

. Then and so

α(x)

α(x′)

. Thus the definition of

θ([x])

is independent of the choice of element from

[x]

we make. Let . Then

Hence

θν

. If

θ′

were another function such that

θ′ν

α,

then for each we would have

Hence

θ′

. Suppose that

θ([x])

θ([x′])

. Then

α(x)

α(x′)

. But then and so

[x]

[x′]

. It

follows that

is injective.

is surjective, then for each there exists such that

α(x)

. But then

θ([x])

and so

also surjective. We have proved that

is a bijection. On the other hand, if

is surjective then so is

because

θν

and both functions on the right-hand side are surjective, which implies that

surjective.

The theorem above may seem abstract, but an example will demonstrate that the idea behind it is

simple.

< previous page page_200 next page >

< previous page page_201 next page >

Page 201

Example 9.2.5 Consider the function

α: X

→

of Example 9.2.2. For convenience, label the blocks of

the partition which

induces on

as follows:

The function

from

/ker

(α)

is therefore given by the following table:

The unique injection from

promised by Proposition 9.2.4 is therefore given by

We shall now show how to adapt Theorem 9.2.4 when the sets are semi-groups and the function is a

homomorphism. Let

α: S

→

be a semigroup homomorphism. As before, we define an equivalence

relation ker

(α)

as follows:

Because

is a homomorphism between semigroups this equivalence relation has an additional property.

Proposition 9.2.6

Let

such that and . Then .

Proof By definition means

α(a)

α(b)

and means

α(c)

α(d)

. Now a is a

semigroup homomorphism and so we have the following equalities:

Thus .

The property described in Proposition 9.2.6 is so important we single it out as the basis of a definition.

Let

be a semigroup and let ~ be an equivalence relation defined on

. We say that ~ is a

congruence

and

implies that

. A ~-equivalence class is called a

congruence class

and the ~-

congruence class containing

is denoted by

[s]

. Elements in the same congruence class are said to be

congruent

. The set of congruence classes is denoted

/~.

Equivalence relations are related to partitions, and congruence relations are special kinds of equivalence

relations, so it is natural to ask what are the special kinds of partition that correspond to congruences?

The next definition

< previous page page_201 next page >

< previous page page_202 next page >

Page 202

provides the answer. Let

be a semigroup. An

admissible partition on S

is a partition

such that if

and

are blocks of the partition, then there is a block

in the partition, necessarily unique, such that

where .

Proposition 9.2.7

Let S be a semigroup. The equivalence relation corresponding to an admissible

partition on S is a congruence on S, and the set of congruence classes of a congruence is an admissible

partition.

Proof Let

be an admissible partition on

and let ~ be the corresponding equivalence relation. We

prove that ~ is a congruence. Let

and

. Then

and

belong to the same block,

say, of

Similarly

and

belong to the same block

. By assumption, where

is a block. Now

and so that . Similarly and so that . It follows that and so

bd,

as required.

Let

be a congruence on

and let

ρ(a)

and

ρ(b)

be two congruence classes. Let and .

Then

a′ρa

and

b′ρb

. Thus

a′b′ρab,

because

is a congruence. It follows that . Thus

. So the set of congruence classes forms an admissible partition.

Let ~ be any congruence on the semigroup

. We shall now show that we can define a binary operation

on the set

/~ in such a way that it becomes a semigroup. To do this, we have to find a way of

multiplying two congruence classes

[s]

and

[t]

. From the above result, we see that

[s][t]

is a subset of

the uniquely determined congruence class

[st]

. It is therefore natural to define . The proof

of the following is now straightforward.

Proposition 9.2.8

Let

be a congruence defined on the semigroup S

Define the binary operation on

the set S

/ ~

Then is a semigroup

It is worth emphasising that

[s][t]

is usually contained in

[st]

rather than equal to it. Nevertheless, it is

usual to denote the product in

/~ by concatenation. The semigroup

/~ is called a

quotient

factor

semigroup

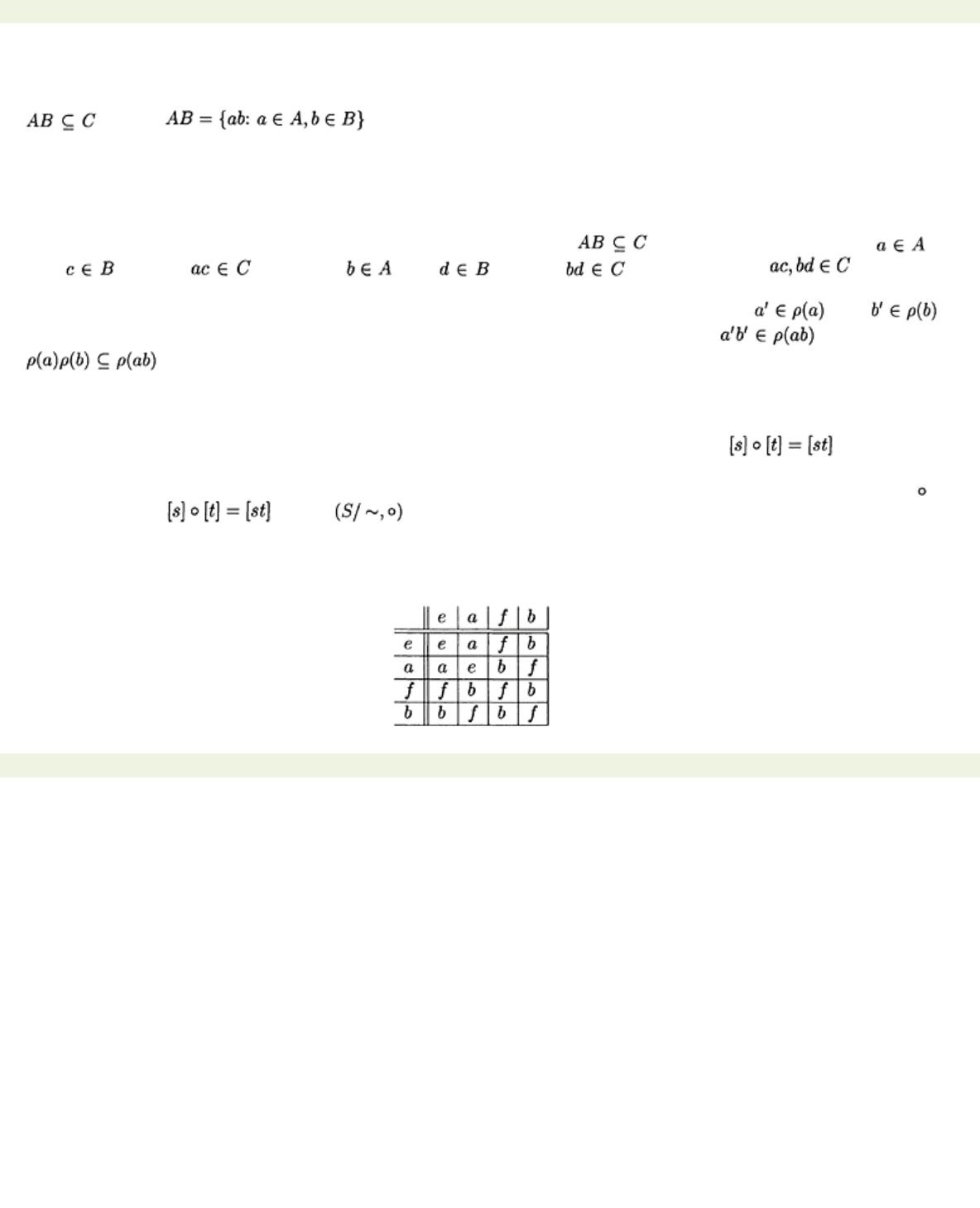
Example 9.2.9 Consider the following semigroup

< previous page page_202 next page >

< previous page page_203 next page >

Page 203

You might like to check that this really is a semigroup. To determine whether the partition

{{e, f}, {a,

b}}

is admissible we proceed as follows: we try to construct the Cayley table of

ρ;

if closure fails at

any point then the partition is not admissible. By definition

{[e], [a]}

. We calculate the products of

the elements in

as subsets of

and determine whether the result is contained in a single block:

•

[e][e]

{e, f}{e, f}

{ee, ef, fe, ff}

{e, f}

[e]

•

[e][a]

{e, f}{a, b}

{ea, eb, fa, fb}

{a, b}=[a]

•

[a][e]

{a, b}{e, f}

{ae, af, be, bf}

{a, b}

[a]

•

[a][a]

{a, b}{a, b}

{aa, ab, ba, bb}

{e, f}

[e]

The partition is therefore admissible. In this case, the product of two congruence classes is equal to a

congruence class rather than simply being contained in one. The Cayley table for

is therefore:

Let ~ be a congruence on

. There is a function

ν: S

→

which maps

[s]

. This function is defined

between two semigroups, so it is natural to ask if it is a homomorphism.

Lemma 9.2.10

Let S be a semigroup and

a congruence on S

Then the function ν: S

→

defined

is a semigroup homomorphism

Proof By definition

ν(ab)

[ab]

[a][b]

ν(a)ν(b)

The function

above is called the

natural homomorphism

associated with the congruence ~. The

following theorem extends Theorem 9.2.4 to semigroups and homomorphisms.

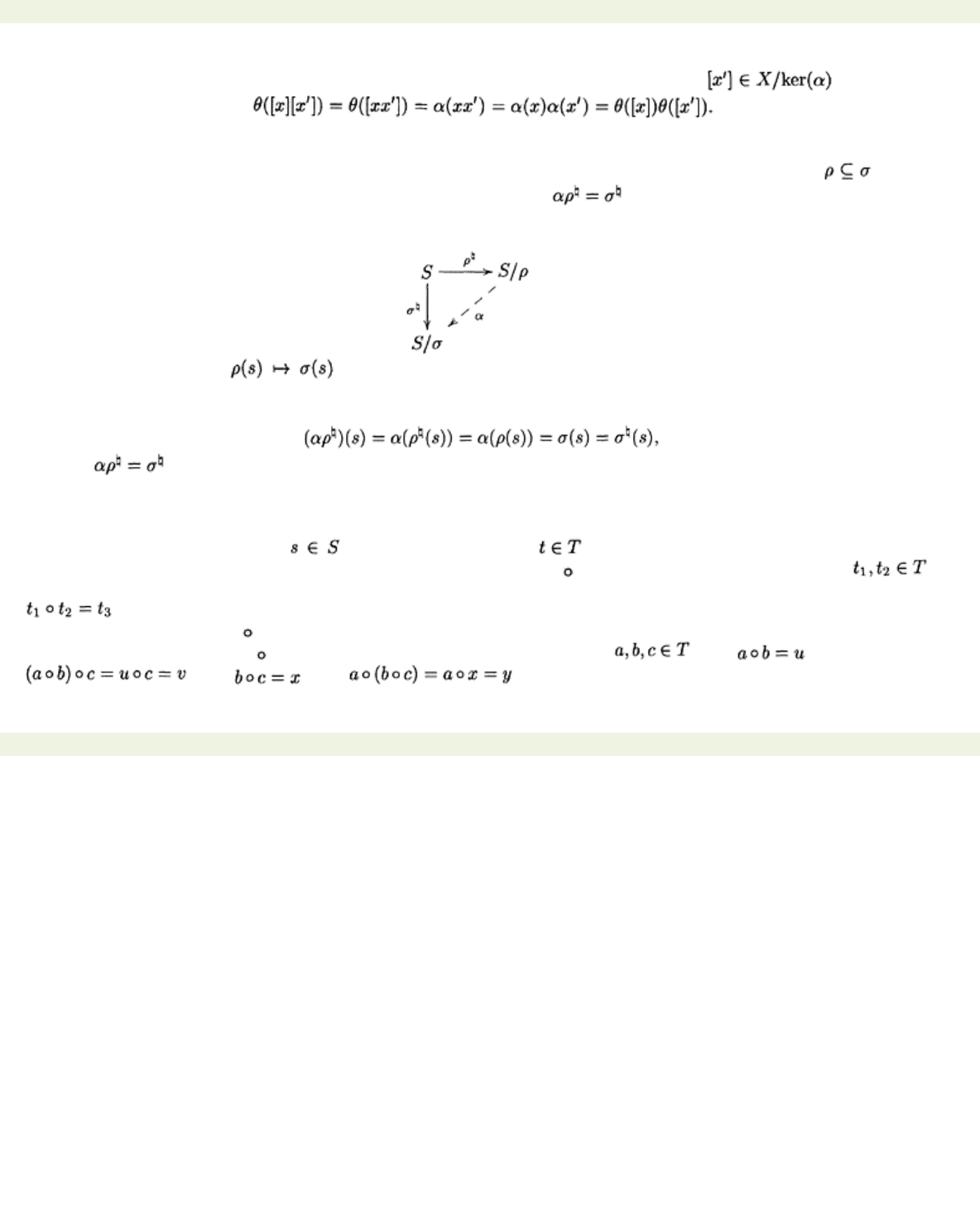
Theorem 9.2.11 (First Isomorphism Theorem)

Let α: S

→

T be a semi-group homomorphism

Then

there is a unique homomorphism θ: S

/ker

(α)

→

T such that θν

In addition, θ is injective. The

homomorphism θ is surjective if and only if α is surjective. If α is surjective, then T is isomorphic to

/ker

(α)

Proof All the set-theoretic results are as in Theorem 9.2.4, it only remains to prove that

and

are

homomorphisms: we proved that the former was

< previous page page_203 next page >

< previous page page_204 next page >

Page 204

a homomorphism in Lemma 9.2.10. To prove that

is a homomorphism, let . Then

The result above tells us that any homomorphic image of a semigroup

can be constructed, up to

isomorphism, by means of a congruence on

Proposition 9.2.12

Let S be a semigroup and let ρ and+be congruences on S such that

. Then

there is a surjective homomorphism α: S

→

σ such that

Proof The diagram below shows the homomorphisms we are given as solid arrows and the

homomorphism we wish to construct is a dashed arrow:

Define

α: S

→

by . Observe that if

ρ(s)

ρ(s′)

then

sρs′

and so

sσs′,

which gives

σ(s)

σ(s′)

. Thus the function

is well-defined. It is a homomorphism because

α(ρ(s)ρ(t))

α(ρ(st))

σ(st),

whereas

α(ρ(s))α(ρ(t))

σ(s)σ(t)

σ(st)

. It is clear that

is surjective. Finally,

so that

Dealing with semigroups described in terms of congruence classes can be inconvenient. However, there

is a simple way around this problem. Let ~ be a congruence on the semigroup

. Choose one element

from each congruence class in any way whatsoever. Denote the set of these elements by

. The key

property of

is that for each there exists a unique such that

. We call

a set of

congruence representatives

for ~. Define a binary operation on

in the following way. Let .

Then

2 is some element in

. By assumption

2 is congruent to a unique element

3 of

. Define

Proposition 9.2.13 (

)

is a semigroup isomorphic to S

/~.

Proof We show first that is an associative binary operation. Let . Let and

. Let and . We have to prove that

. We use the fact

that ~ is a congruence. Now

and

. Thus

abc

. Similarly

and

< previous page page_204 next page >

< previous page page_205 next page >

Page 205

abc

. Thus

. But and so by assumption

as required.

Define

θ: S

/~→

θ([s])

where and

. This is a well-defined function, for if

[s]

[s′]

then

s′

and so

s′

. Thus

θ([s′])

Suppose that

θ([s])

θ([s′])

. Then there is such that

s′

and so

s′

. It follows that

[s]

[s′]

Thus

is injective. Let . Then

θ([t])

and so

is surjective. We have proved that

is a bijection.

To show that

is a homomorphism, let . Let

and

where

u, .

Then

ab,

and . Thus . Then

and

It follows that

and so

is a bijective homomorphism, and consequently an isomorphism.

The example below illustrates the above result.

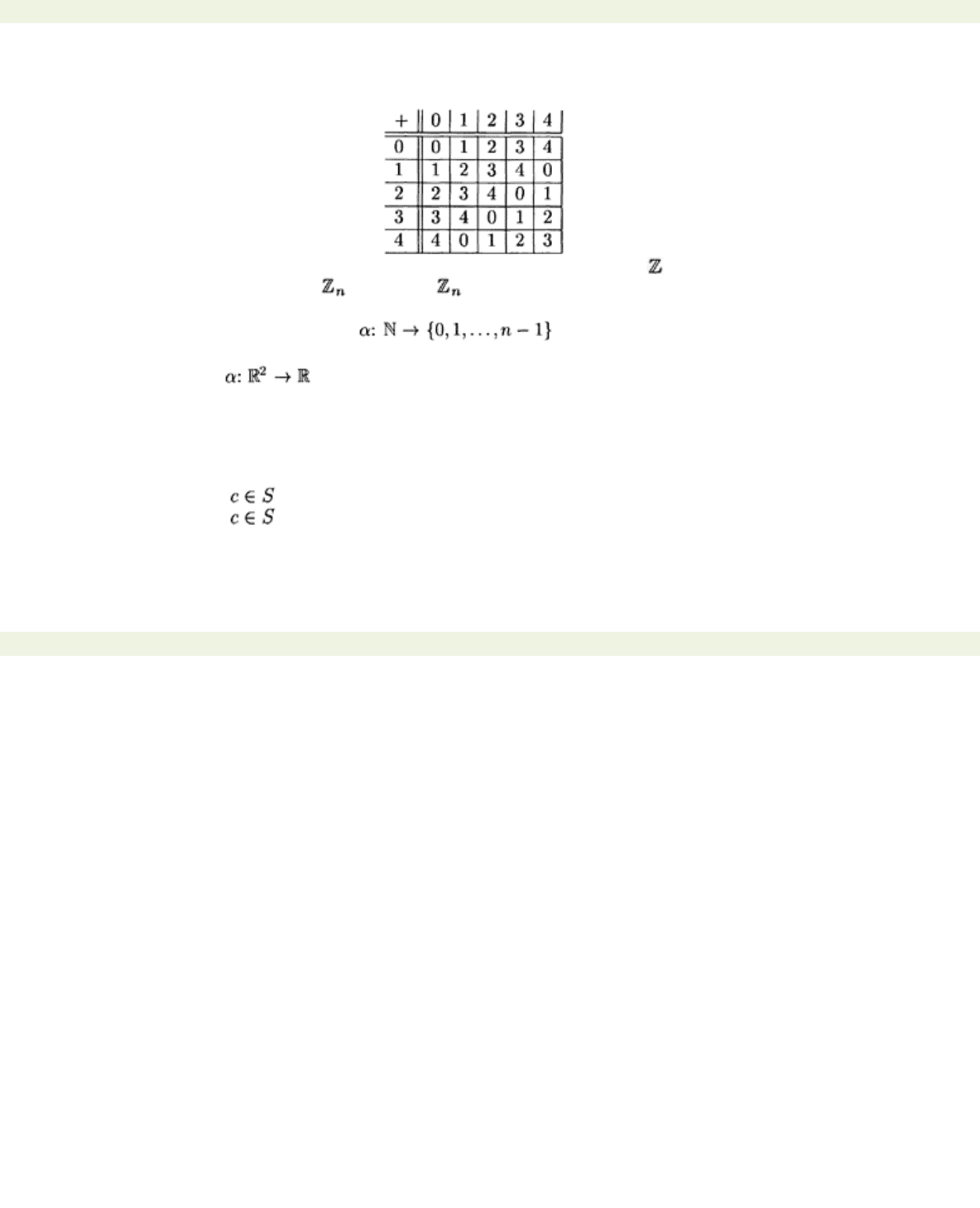
Example 9.2.14 We work with the monoid ( , +). Define = on as follows:

It is an easy exercise to check that = is an equivalence relation. It is also a congruence. To see why, let

and suppose that

and

. Then

−

and

−

for some integers

and

Thus (

)−(

(

). Hence

which shows that = is a congruence. There are 5

congruence classes:

• {…, −10, −5, 0, 5, 10,…},

• {…, −9, −4, 1, 6,…},

• {…, −8, −3, 2, 7,…},

• {…, −7, −2, 3, 8,…},

• {…, −6, −1, 4, 9,…}.

The binary operation on

is simple but unwieldy. For example,

is defined to be the =-congruence class containing, for example, 2+3=5. Thus

< previous page page_205 next page >

< previous page page_206 next page >

Page 206

An obvious set of congruence representatives in this case is {0, 1, 2, 3, 4}. The Cayley table of this set

with the binary operation defined according to Proposition 9.2.13 is

The above example can be extended to any modulus

≥2 defined on both for addition and for

multiplication. In this way, both ( , +) and ( , ×) are monoids.

Exercises 9.2

1. Let

≥2 be a fixed integer. Define by

α(a)

where

is the remainder 0≤

when a is divided by

. Describe the corresponding equivalence relation.

2. Define the function by

α(x, y)

−

. Describe the corresponding equivalence relation.

3. Use the semigroup of Example 9.2.9 to show that the equivalence relations ~ below are admissible.

(i)

{{e, a}, {f, b}}.

(ii)

{{e}, {a}, {f, b}}.

In each case, draw up the Cayley table of

/ ~.3

4. Let ~ be an equivalence relation on a semigroup

satisfying the following two conditions:

(LC)

and implies

(RC)

and implies

Prove that ~ is a congruence. Conversely prove that every congruence satisfies (LC) and (RC).

An equivalence relation on a semigroup is called a left congruence if it satisfies condition (LC), and is

called a

right congruence

if it satisfies (RC)

Thus

3Example 9.2.9 and this question are taken from [67].

< previous page page_206 next page >