Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_167 next page >

Page 167

Proposition 7.5.16

Every regular expression has only a finite number of dissimilar quotients.

Proof The proof is by induction but we have already done most of the work in Propositions 7.5.3 and

7.5.15. Suppose that

and

each have a finite number of dissimilar quotients. We prove that the same

is true for

M, LM,

and

*. The result is clear for

so we need only deal with the last two cases.

To prove that

has only finitely many dissimilar quotients we use Proposition 7.5.15(i). Let be the

finite set of dissimilar quotients of

and let be the finite set of dissimilar quotients of

. For each

we have that

−1

(LM)

is of the form, where and is a union of some elements

. Working with set notation is the same as assuming the associative, commutative, and

idempotency laws for union. It follows that if

and

each have finitely many dissimilar quotients so too

does

To prove that

* has only finitely many dissimilar quotients, we use Proposition 7.5.15(ii). For each

we have that

−1

* is of the form

where is a a union of some elements of . Once

again,

* has only finitely many dissimilar quotients.

The above result reassures us that as long as we at least recognise when two quotients are similar,

then our algorithm will terminate.

It remains to explain the implications for the automaton we construct of failing to recognise the equality

of two quotients. Suppose that

and

are two quotients of

such that

but we fail to recognise

this when constructing the transition tree used in the Method of Quotients. In the automaton we

construct from the transition tree,

and

will label two different states. These states will be

indistinguishable, because for each input

we have that iff

Exercises 7.5

1. Prove Lemma 7.5.2.

2. Complete the proof of Proposition 7.5.6.

3. Let

{a, b}

. For each of the languages below find the minimal automaton using the Method of

Quotients.

(i)

ab.

(ii) (

(iii)

(ab)

(iv) (

)*.

< previous page page_167 next page >

< previous page page_168 next page >

Page 168

(v) (

)*.

(vi)

(vii)

(

(viii) (

aab

(

)*.

4. Prove Lemma 7.5.12.

5. Fill in all the steps missing from Example 7.5.13.

6. Let

be a language over the alphabet

. Prove that

J.H.Conway [35] says that this result is “both Taylor’s theorem and the mean value theorem” for the

theory of quotients of languages.

7. Calculate the quotients of {

anbn: n

≥0}.

7.6 Summary of Chapter 7

•

Reduction of an automaton:

From each deterministic automaton A we can construct an automaton A

with the property that each pair of states in A is distinguishable and

(A). The automata A

and A

are isomorphic and both are reduced and accessible.

•

Minimal automaton:

Each recognisable language

is recognised by an automaton that has the

smallest number of states amongst all the automata recognising

this is the minimal automaton for

Such an automaton must be reduced and connected, and any reduced and connected automaton must

be minimal for the language it recognises. Any two minimal automata for a language are isomorphic.

•

Method of Quotients:

The minimal automaton corresponding to the language described by a regular

expression

can be constructed directly from

by calculating the quotients of

7.7 Remarks on Chapter 7

The minimisation algorithm, Algorithm 7.2.5, goes back to Huffman [69] and Moore [95]. The version I

have presented is an informal version of the one described in [65]. An efficient algorithm can be found

in [64]. The ‘Method

< previous page page_168 next page >

< previous page page_169 next page >

Page 169

of Quotients’ and, indeed, most of Section 7.5, is due to Brzozowski [19], although he points out that

quotients had been used by earlier writers. Brzozowski uses the term ‘derivative’ instead of ‘quotient’

and writes

DuL

rather than our

−1

. This terminology is based on the following two results

(Proposition 7.5.3(ii) and (iii)):

•

(

DaL

DaM,

•

Da(LM)

(DaL)M

δ(L)(DaM),

which are analogous to the following two results in calculus:

•

Conway [35] even goes so far as to have a chapter entitled “The differential calculus of events,” where

‘event’ is an older term for ‘language.’

< previous page page_169 next page >

< previous page page_170 next page >

Page 170

This page intentionally left blank.

< previous page page_170 next page >

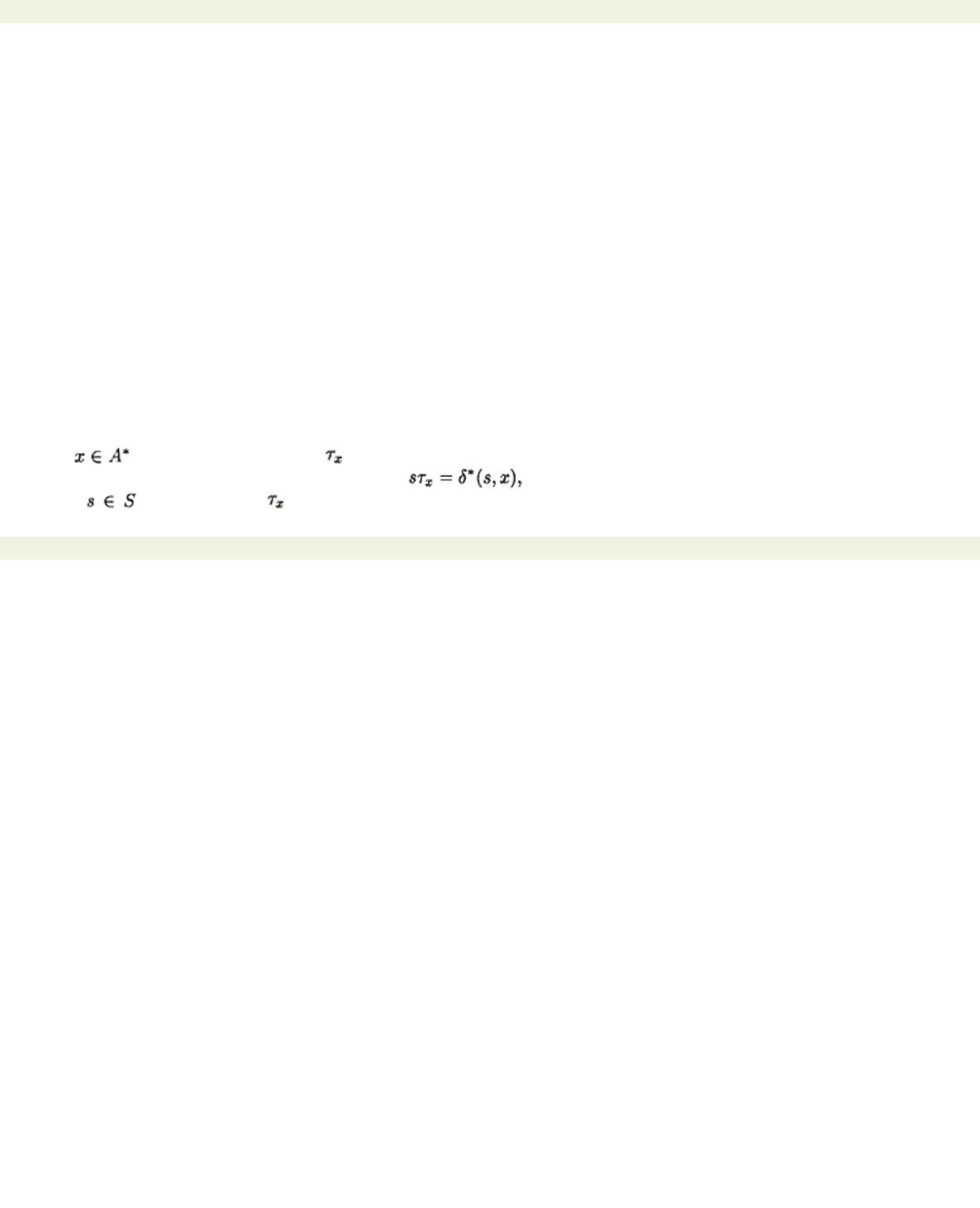
< previous page page_171 next page >

Page 171

Chapter 8

The transition monoid

In this chapter, we take the first steps in describing an algebraic method for answering questions about

recognisable languages. The basic idea is simple. Consider a complete deterministic automaton. Each

input string to the automaton defines a function from the set of states to itself. Although there are

infinitely many input strings, there can only be a finite number of distinct functions that arise in this way

because our machine has only a finite number of states. Thus the set of input strings leads to a finite

set of functions defined on the set of states. This set of functions has an additional property: the

composition of any two of them is again in the set. Because composition of functions is associative, we

therefore obtain a set equipped with an associative binary operation. Such a set is called a ‘semigroup,’

and because it has only finitely many elements, the semigroup in question is a ‘finite semigroup.’ Thus

with each automaton we can associate a finite semigroup. Now suppose we have a recognisable

language. This is accepted by an essentially unique minimal automaton by Theorem 7.4.2 and, by the

process above, we can associate a finite semigroup with this machine. It follows that with each

recognisable language we can associate a finite semigroup. We shall see in Chapters 9–12 that this

semigroup can be used to obtain important information about the language in question.

8.1 Functions on states

In this chapter, we shall be interested in the effect that input strings have on the set of states of an

automaton. We begin by making clear what we mean by this. Let A=

(S, A, i, δ, T)

be an automaton. For

each

we define a function from

as follows:

where . The function describes the

effect

of the string

on the set of states

< previous page page_171 next page >

< previous page page_172 next page >

Page 172

Notation Notice that we have written the function to the right of its argument rather than to the

left. This is because automata process input from left to right.

The function can be explicitly described by means of its row form. To see how, we assume that an

ordering of the states has been chosen. By the

row form of

we mean a table with two rows: the first

consisting of the states

listed in their order and the second consisting of the corresponding values .

Example 8.1.1 Consider the following automaton A:

The transition table for this automaton is

We have omitted the usual labelling of initial and terminal states in the transition table because they will

play no role in what we want to do. Let us calculate the effect of the string

. To do this we use the

extended transition function

*. We have that

1·

=(1·

)·a=1·

=2,

2·

=(2·

)·a=3·

=3,

3·

=(3·

)·a=3·

=3.

Thus is the function:

In row form, this function is represented by the table

More generally, we shall be interested in functions defined on any set to itself. Let

be a set, and let

be a function defined from

to itself. We shall write arguments on the left so that if then

(x)α

the value of

< previous page page_172 next page >

< previous page page_173 next page >

Page 173

. We shall usually write

xα

unless this could cause ambiguity. If

is also a function from

to itself,

then we can define a new function

from

to itself as follows:

In other words, we evaluate

and then

xα

. We call the

composition of α and β

. We shall

usually omit and write simply

αβ

Example 8.1.2 Let

={1, 2, 3, 4} and let

and

be the two functions that map

defined as

follows using row form:

If we compose the functions in accordance with our definition above we obtain the new function

αβ:

→

which is given by

Let us see how this result was obtained. The composite function

αβ

maps elements of

to elements of

. Thus the composite has the form:

Our job is to fill in the question marks. We begin with the first. To calculate 1

(αβ)

we have to calculate

)

β;

thus we calculate the effect

has on 1 and then the effect

has on the result:

We can therefore fill in the first question mark:

To fill in the second question mark we have to calculate 2

(αβ);

this is just

We can therefore fill in the second question mark:

The remaining two question marks can be calculated in the same way. The only point that has to be

remembered is that we always work from left to

< previous page page_173 next page >

< previous page page_174 next page >

Page 174

right. If we compose the functions in the opposite order we obtain the new function

βα: S

→

which is

given by

Let

be a set. Denote by

T(X)

the set of all functions

α: X

→

. If

={1,…,

} then we usually write

rather than

({1,…,

}). The

identity function on X,

denoted by

ι,

is the function from

defined by

xι

for each . The set

T(X)

equipped with composition of functions and the distinguished function

is called the

full transformation monoid on X

. The word ‘transformation’ is also used to mean ‘function’;

the meaning of the word ‘monoid’ will be given in Section 8.4.

Proposition 8.1.3

Let

Then α(βγ)

(αβ)γ

Furthermore, ια

αι

Proof Let . Then by definition,

A similar calculation shows that

Thus

α(βγ)

(αβ)γ

as required. The proof of the last assertion is left as an exercise.

The fact that

α(βγ)

(αβ)γ

is similar to a property we met in Section 1.1: composition of functions, like

concatenation of strings, is associative; when we compose three functions it does not matter where we

put the brackets. As we shall show in Chapter 9,1 more is true: in computing the composition of

elements

…αn

it does not matter where we put the brackets. However, as Example 8.1.2

shows, the order in which we compose functions is important. If and

is a positive integer

then we shall write

αn

to mean the composition of

with itself

times; if

=0 then we define

The proof of the following, except the last claim, is just a reformulation of Proposition 1.5.4. We leave it

all as an exercise.

Proposition 8.1.4

Let

(S, A, i, δ, T) be an automaton

Then for all x, . In addition

, the identity function on S.

The above result, together with the associativity of function composition, has the following consequence.

Let

…an

. Then .

1 Specifically, Theorem 9.1.1.

< previous page page_174 next page >

< previous page page_175 next page >

Page 175

Example 8.1.5 We compute in the automaton of Example 8.1.1. From our result above, this is

equal to

which is the composition of the following three functions in the given order:

This is simply

Let A=

(S, A, i, δ, T)

be an automaton, and let . We say that

x has the same effect as y

(

in the

automaton

A), written

if . Strictly speaking we should write =A to make clear the

dependence of = on the automaton, but we shall always use the simpler notation.

Proposition 8.1.6

Let

(S, A, i, δ, T) be an automaton

Then the relation

which

defines on A

an equivalence relation that has the following additional property: if and x

x′ and y

y′ then

x′y′

Proof The proof that = is an equivalence relation is left as an exercise.

To prove the second claim, we are given that

and . By Proposition 8.1.4,

Thus and so

x′y′

Exercises 8.1

1. List the elements of

and calculate all possible compositions.

2. If |

show that |

T(X)

3. Consider the automaton A below:

Write down , and in row form. Hence calculate the effects of

, b

and

< previous page page_175 next page >

< previous page page_176 next page >

Page 176

4. Complete the proof of Proposition 8.1.3 by showing that

ια

αι

5. Prove Proposition 8.1.4.

6. Complete the proof of Proposition 8.1.6 by showing that = is an equivalence relation.

8.2 The extended transition table

Let A=

(S, A, i, δ, T)

be an automaton. As we saw in Section 8.1, each string defines a function

from the set of states of A to itself. We shall be interested in

all

the functions that arise in this way.

In other words, the set of functions,

The question now arises of how we can find them in a systematic way. The transition table of A tells us

how to process individual input

letters:

the columns are labelled by the input letters, the rows by the

states, and the entry in row

and column

δ(s, a)

. Thus the effects of the input letters can be read

off from the columns of the transition table. In order to determine the effects of input

strings,

we have

to use the extended transition function

*. In principle, we could draw up an ‘extended transition table’

in which the columns were labelled by the strings in

*. Of course, this is not practical because there

are infinitely many strings. However, as we shall show, all the information in the extended transition

table can be presented in entirely finite terms. Before we explain how to do this in general, we give an

example.

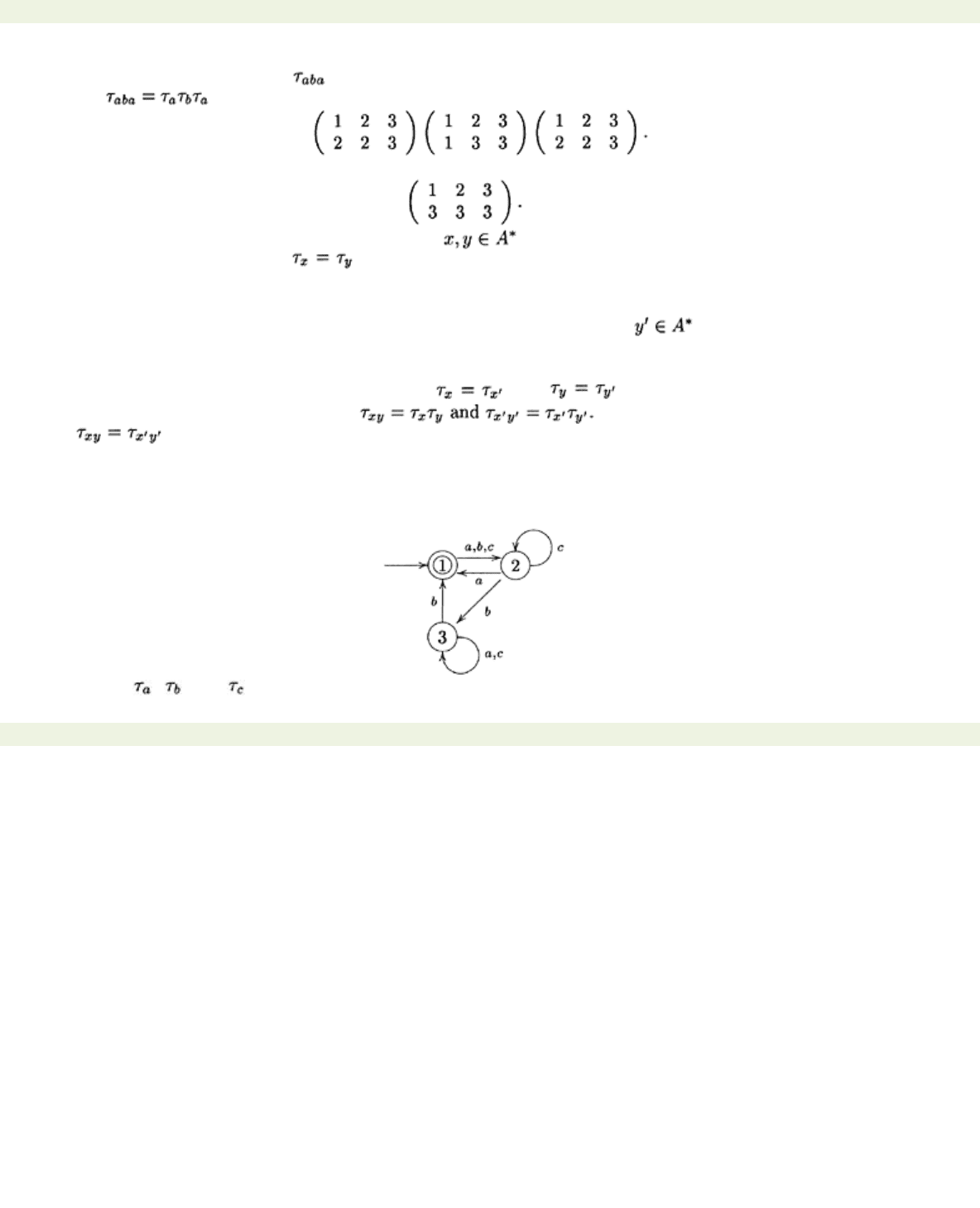
Example 8.2.1 Consider the following automaton A:

The transition table of A is given below:

We wish to describe the effects of

all

the strings in

*. We shall do this by expanding the transition table

into an ‘extended transition table’ by adding extra columns. At the same time we shall show how to get

around the problem of having infinitely many columns. The first point to note is that our extended

transition table is likely to have many columns, so it makes sense to

< previous page page_176 next page >