Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_177 next page >

Page 177

construct them vertically rather than horizontally. Thus the table above will be represented as follows:

This has the added benefit that we can now immediately read off from this table the row form of the

functions and

The strings in

* can be listed in the tree order:

From the definition of the extended transition function we know that is the identity function. We may

therefore incorporate the effect of

as follows:

Now we turn to the strings of length 2. We calculate the effect of

by computing

;

this is just

In the same way, we can calculate the effects of the other strings of length 2:

and

Our extended transition table now has the following form:

< previous page page_177 next page >

< previous page page_178 next page >

Page 178

I have marked certain rows with an ‘x.’ I shall explain why below. We could continue extending our table

by considering the effects of all strings of length 3; however, we do not need to. This is because each

string of length 2 has the same effect on the states of A as a string of length at most 1; we have

highlighted these rows with an ‘x.’ Thus we have the following:

We now have all the information needed to compute the effect of

any

input string with the minimum

effort. Consider the first few strings of length 3 in the tree order:

These calculations are correct by Proposition 8.1.6. It should be clear that every string of length 3 has

the same effect as one of the strings

ε, a, b

. More generally, every string in

* has the same effect as

one of these three strings.

The above example is typical: although there are infinitely many input strings there are only finitely

many effects that these input strings can have, because the automaton has only finitely many states. As

a result, the extended transition table, which is potentially infinite, can in fact be represented in finite

terms. It is this finite table that we shall call the

extended transition table

. The algorithm below is similar

to the construction of the transition tree of an automaton, described in Section 3.1, for the following

reason. If A=

(S, A, i, δ, T)

is a deterministic automaton with

states

,…sn},

construct a new

automaton B as follows: the set of states is

Sn,

the initial state is

,…, sn),

the transition function is

,…, sn)

1·

a,…, sn

a),

the terminal states are chosen arbitrarily. The algorithm below just

constructs the transition tree of B, but does so in tabular form.

Algorithm 8.2.2 (The extended transition table) Choose an order for the alphabet, and

accordingly order all input strings using the tree order. Construct a table whose columns are labelled by

the states of A in some order and whose rows will be labelled by some of the strings in

*. In addition,

certain rows will be marked with a cross.

(1) To start the algorithm off, the first row is labelled

and contains the states of A in the given order.

For each

calculate

δ(s, a)

for each state

if the resulting row of states is a repeat of an earlier

row, then mark it with a cross. We say that this row is ‘closed.’

< previous page page_178 next page >

< previous page page_179 next page >

Page 179

(2) The general procedure runs as follows: assume that we have completed the rows corresponding to

strings of length

. For each string

of length

in turn, which is

not

closed, compute for each the

effect of

on the states: if the resulting row of states is a repeat of an earlier row then mark it with a

cross.

(3) If all rows corresponding to strings of length

are closed then the algorithm terminates.

Here is an example of this algorithm in action.

Example 8.2.3 Consider the automaton A of Example 8.1.1:

We shall calculate its extended transition table. The algorithm begins with the following three rows:

In this case, there are so far no repeats. We therefore have to calculate the effects of all the strings

aa,

ab, ba

and

. We obtain the following:

We see that

and

. The next step of the algorithm considers the effect of the following strings:

aba, abb

and

baa, bab;

we do not need to consider the effects of

and

or of

and

because the rows corresponding to

< previous page page_179 next page >

< previous page page_180 next page >

Page 180

2 and

2 are closed. We obtain the following:

At this point our algorithm terminates because all strings of length 3 that appear in the table are closed.

There is a more compact way of recording the information contained in the extended transition table.

Let us first consider only those rows of the table that are not closed. The corresponding table is called

the

table of representatives

. In the case of Example 8.2.3, this is the following table:

Now we turn to the closed rows. For each closed row labelled

of the extended transition, the string

has the same effect as a unique representative

. We write

and call this a

relation

. The relations

arising from Example 8.2.3 are as follows:

We have listed them according to the tree order of their left-hand sides. It is clear that the extended

transition table contains exactly the same information as the table of representatives and the list of

relations. Algorithm 8.2.2 can easily be modified to yield the table of representatives and relations

directly.

< previous page page_180 next page >

< previous page page_181 next page >

Page 181

Algorithm 8.2.4 (Representatives and relations) We order the alphabet, and accordingly order all

input strings using the tree order. Construct a table whose columns are labelled by the states of A in

some order and whose rows are labelled by some of the strings in

*. We shall also construct a list of

relations.

(1) To start the algorithm off, the first row is labelled

and contains the states of A in the given order.

For each

calculate

for each state

if the resulting row of states is a repeat of an earlier row

labelled

then add

to the list of relations and erase the new row labelled

(2) The general procedure runs as follows: assume that we have completed the rows corresponding to

strings of length

. For each string

of length

in turn that appears in the table compute for each

the effect of

on the states: if the resulting row of states is a repeat of an earlier row labelled

then add

to the list of relations and erase the new row labelled

(3) The algorithm terminates when for some

all strings

of length

that appear in the table, all the

strings

for each lead to no new rows.

Once we have the table of representatives and relations produced by this algorithm there is a simple

algorithm for computing the effect of an arbitrary string over the input alphabet.

Algorithm 8.2.5 (Reduction of strings) Let A be an automaton and assume that we have applied

Algorithm 8.2.4 to A to obtain a table of representatives and a list of relations. Let

…an

be a non-

empty string over the input alphabet of A. The algorithm computes the unique representative

such

that

is a representative then we are done, otherwise

has a prefix

such that

is a relation. Let

uw′

. Then

uw′

vw′

. By construction |

vw′|<|w

|. Repeat this procedure with

replaced by

vw′

The algorithm terminates at one of the representatives

that will satisfy

by construction.

Example 8.2.6 Let us apply Algorithm 8.2.5 to the string

aababbbaa

using the table of representatives

and relations of Example 8.2.3. We obtain the following sequence of strings; prefixes used at each step

are underlined and the results of applying each relation are highlighted in bold:

< previous page page_181 next page >

< previous page page_182 next page >

Page 182

Thus

aababbbaa

Algorithms 8.2.4 and 8.2.5 together provide a fast way of computing the effect of an input string on the

states of an automaton: Algorithm 8.2.4 is carried out once to provide a table of representatives and a

list of relations, and then we implement Algorithm 8.2.5 for each input string we are interested in. It

remains for us to prove our claims.

Theorem 8.2.7

Algorithm 8.2.4 always halts, and the table of representatives and list of relations can

be used to calculate the effect of each input string in accordance with Algorithm 8.2.5.

Proof The proof that Algorithm 8.2.4 always halts is the same as the proof that the construction of the

transition tree of an automaton always halts, as explained prior to Algorithm 8.2.2.

It remains to show that we can compute the effect of any input string using Algorithm 8.2.5. We prove

the following: for each

there exists a representative

x′

such that

x′

that can be found using

Algorithm 8.2.5. This is trivially true for strings of length 0. Assume this is true for all strings

of length

at most

. We prove it is true for all strings of length

+1. Let

be a string of length

+1. Then

where

is a string of length

and . By assumption, we may use Algorithm 8.2.5 to find a

representative

y′

such that

y′

. Thus by Proposition 8.1.6, we have that

y′a

. Now

y′

is a

representative so according to Algorithm 8.2.4, either

y′a

is a representative, in which case we are done,

or it is equivalent to a representative

y″

Exercises 8.2

1. Calculate the extended transition table, and find all the relations for the following automata.

(i)

< previous page page_182 next page >

< previous page page_183 next page >

Page 183

(ii)

(iii)

8.3 The Cayley table of an automaton

In the last two sections, we have developed ways of calculating the effects of all input strings. This is

not intended to be an end unto itself: it is what we can do with them that is interesting. The first thing

we shall do is discard some of the information obtained from Algorithm 8.2.4.

Example 8.3.1 Consider the table of representatives and relations for the automaton in Example 8.2.3.

Our first step is to omit some of the information contained in the table of representatives: we are

interested in the representatives themselves but not their effects. There are three equivalent ways of

doing this.

Method 1 We represent this information as follows:

before the colon we write the representatives and after the colon we write the relations. We call this a

presentation

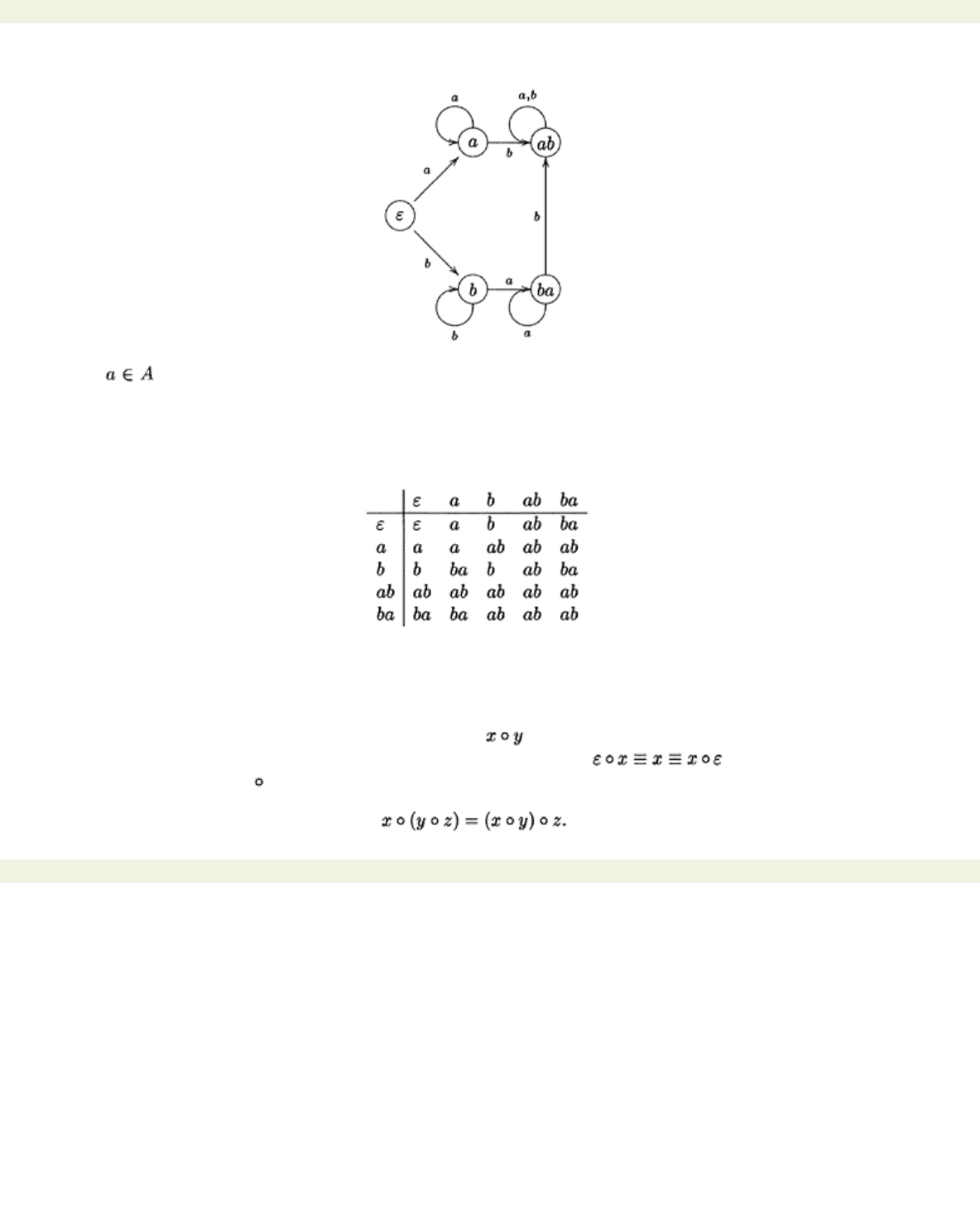
Method 2 The information in a presentation can also be represented diagrammatically in terms of a

labelled directed graph called the

Cayley graph

2This is not the most general definition of ‘presentation’ in semigroup theory, but it is the only one we

shall use in this book.

< previous page page_183 next page >

< previous page page_184 next page >

Page 184

the automaton:

This was constructed as follows: the vertices are labelled by the representatives; for each vertex

and

for each

we calculate the representative

and then draw an arrow from vertex

to vertex

labelled by

Method 3 We have seen that Algorithm 8.2.5 enables us to calculate for each string

a representative

such that

. In particular, we can apply this algorithm to the concatenation of two representative.

We draw up a table, called a

Cayley table,

whose rows and columns are labelled by the representatives

and where the entry in row

and column

is the unique representative

such that

The presentation, the Cayley graph, and the Cayley table contain the same information in different

forms. Given one we can calculate the other two.

We shall be particularly interested in the Cayley tables of automata. As we shall see there are patterns in

such tables that give us information about the language accepted by the automaton.

The Cayley table of an automaton is simply a way of describing the following operation on the set of

representatives: given representatives

and

then is defined to be the representative

such that

. The empty string

is a representative and it is clear that . The most important

property of the operation

is the following.

Proposition 8.3.2

Let x, y, z be three representatives. Then

< previous page page_184 next page >

< previous page page_185 next page >

Page 185

Proof We calculate first

Let

yz,

where

is a representative, and let

xu,

where

is a

representative. Thus

. Now

means and

means . In a

similar fashion, if

then we can show that . It follows that

v′

. But both

and

v′

are representatives and so

v′,

as required.

Exercises 8.3

1. Let

{a, b},

and consider the following languages:

(i)

(ii)

(iii)

For each language find:

(a) The minimal automaton A.

(b) The extended transition table of A.

(d) The Cayley table.

8.4 Semigroups and monoids

The Cayley table of an automaton is an example of a semigroup. This important idea will figure

prominently from now on, so in this section, we shall define what they are and give some examples.

Let

be a set. Any function

α: X

→

is called a

binary operation

. If then the value

(x, y)

α(x, y)

. Two examples of binary operations on the set are the function that maps

(a,

and the function that maps

(a, b)

. Notice that we write the binary operation in both

cases

between

the two inputs. This convention is usually adopted for all binary operations. Another point

to notice is that different binary operations may be defined on the same set. For this reason, we regard

a binary operation as an ordered pair: (

*) where

is the set and * is the specific binary operation. So

both ( , +) and ( , ×) are different binary operations on the same set.

Binary operations can be classified acording to the properties they enjoy. Let (

*) be a binary

operation. We say that it is

associative

for all . A set equipped with an associative binary operation is called a

semigroup

. If (

*) is

a semigroup then we often say that

is a semigroup

with respect to

the operation * or

under

the

operation *.

< previous page page_185 next page >

< previous page page_186 next page >

Page 186

If (

*) is a semigroup, then an element is called an

identity

for the binary operation * if

for all

. An element is called a

zero

for all

. The identity element does not change anything, whereas the zero makes everything into a

zero.

Semigroups will usually be denoted by capitals such as

S, T,…

. When dealing with general semigroup

operations, for example in proofs, it is usual to denote the operation by concatenation, however when

dealing with specific examples of semigroup operations we use the appropriate symbol for the binary

operation.

Proposition 8.4.1

A semigroup S has at most one identity element, and at most one zero.

Proof Suppose that

and

are both identity elements of

. This means that

and

for

all . We calculate the product

in two different ways. First,

is an identity element and so

Second

is an identity element and so

. Thus

and so

. Therefore if a semigroup

has

an identity element

it is unique.

Now let

and

be two zeros in

. Then

and

for all . Thus

and

from

which we get that

A semigroup with an identity is called a

monoid

. It follows that if a semi-group has an identity it has

exactly one, and so we can talk about

the

identity of a monoid. Similarly we can talk about

the

zero of a

semigroup if it has one.

Let

be a semigroup, and let 1 be a symbol not in

. Put and define a product on this set

as follows: if

then

is their product in

and 1

1 for all and 11=1. Then

1 is a

monoid with identity 1.3

A semigroup (

*) is said to be

finite

is a finite set and

infinite

otherwise. Finite semigroups (

can be described by means of

Cayley tables:

this is a table with rows and columns labelled by the

elements of

and with the element in row

and column

being

. We first met Cayley tables in

Section 8.3. A semigroup (

*) is said to be

commutative

for all

3Readers should be aware that some authors define

1 to be

when

is already a monoid.

< previous page page_186 next page >