Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_207 next page >

Page 207

a congruence is an equivalence relation that is both a left and a right congruence.

5. Let

≥2 be an integer. Consider the monoid ( , +). Define

(i) Prove that = is a congruence on with respect to addition.

(ii) Show that is a set of congruence representatives.

(iii) Draw up the Cayley table for (

, +).

Repeat the above question for the monoid (

, ×). In the case of (iii), draw up the Cayley table for ( ,

×).

6. Let

be an equivalence relation on a semigroup

. Define as follows: iff

xayρxby

for all

. Show that is a congruence on

contained in

ρ,

and that if

is any congruence on

contained in

then .

The congruence is the one that best approximates the equivalence relation ρ. There is an important

application of this result. Let A and B be two finite alphabets. Let f: A

+→

B be any function

Then f

induces an equivalence relation

ker

(f) on A

by Lemma 9.2.1. The largest congruence contained in

ker

(f) is denoted

It follows that A

+/=

f is a semigroup

This semigroup is the starting point for John

Rhodes’ theory of sequential functions. See

Chapter 5 of [5] for a discussion of this theory.

A special case of this construction occurs when B=

{0, 1}.

The function f is then determined by the

subset of A

consisting of all those strings such that f(x)

=1.

Such strings form a language

. It is easy to check that the congruence

f is defined by x

f y iff for all

The semigroup A

+/=

f is called the

syntactic semigroup

of the language L

9.3 The transition monoid of an automaton

We now have all the ideas necessary to understand Chapter 8.

Let A=

(S, A, i, δ, T)

be an automaton. We have seen that the function defined by

is a monoid homomorphism whose image is the transition monoid

(A) of A. We now look at

the congruence that induces on

*. This is nothing other than the relation = defined in Section 8.1. It

follows that

*/= is isomorphic to the image of by Theorem 9.2.11. Thus

*/= is isomorphic to the

transition monoid of A.

The monoid

*/= can also be described by picking representatives of the congruence classes as in

Proposition 9.2.13. There are many ways of doing this, but let us do so by picking from the class

[x]

the

string

that is smallest

< previous page page_207 next page >

< previous page page_208 next page >

Page 208

in the tree order. The monoid we obtain is isomorphic to

*/=, and is nothing other than the monoid of

representatives as described in Chapter 8.

If two semigroups are each isomorphic to a third, they are isomorphic to each other (by Question 10 of

Exercises 9.1). We conclude that the transition monoid and the monoid of representatives are

isomorphic to each other. We summarise what we have found in the following theorem.

Theorem 9.3.1

Let

(S, A, i, δ, T) be an automaton and let be the map associating

with x the function it induces on S

The kernel of

is the congruence

The semigroup A

*/=

isomorphic to the transition monoid of

it is also isomorphic to the monoid of representatives of

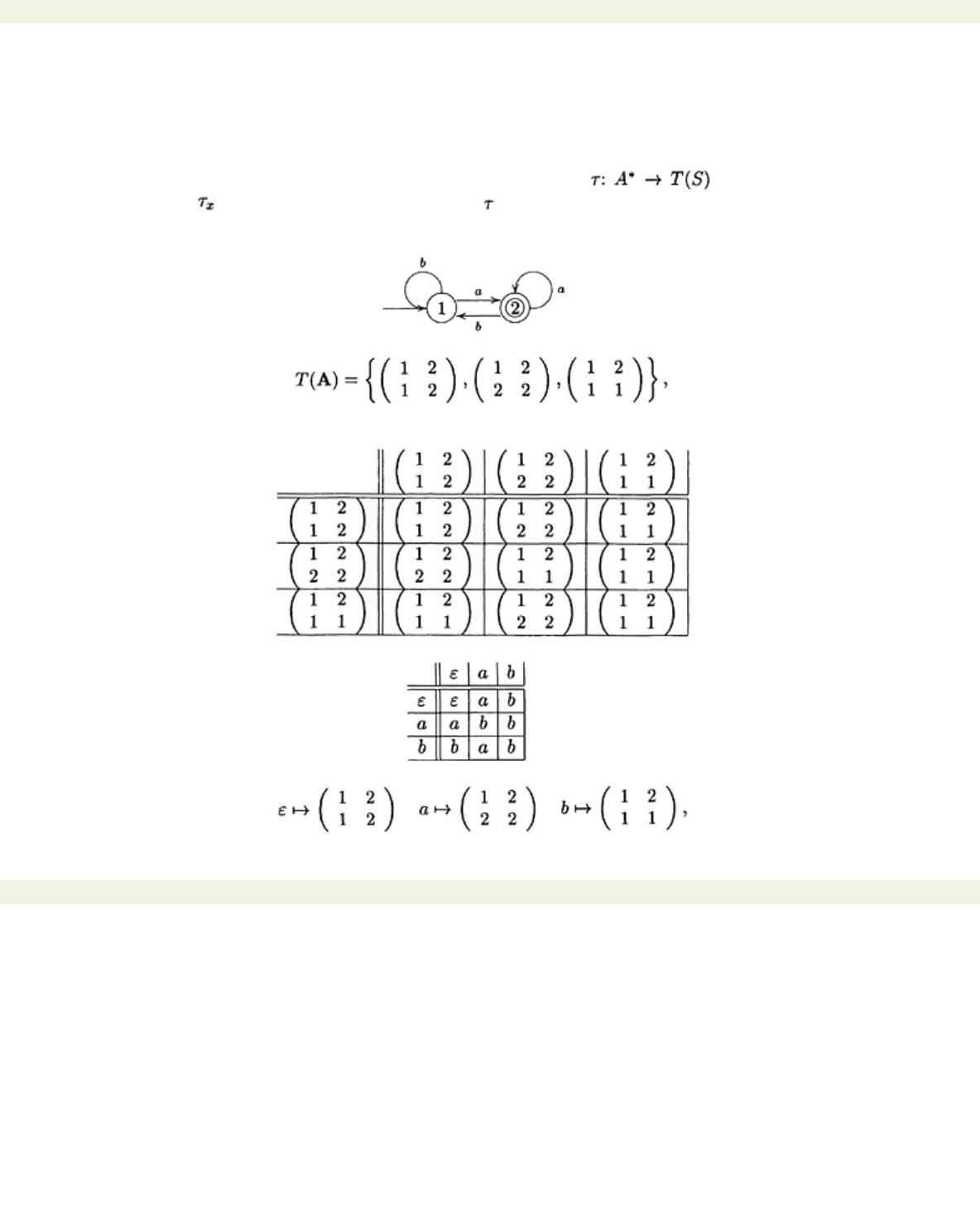
Example 9.3.2 We return to the automaton A of Example 8.2.1:

The transition monoid consists of the following elements:

and the monoid of representatives consists of the elements

{ε, a, b}

. The Cayley table of the transition

monoid is

The Cayley table for the monoid of representatives is

The isomorphism between these two monoids is determined by

respectively.

< previous page page_208 next page >

< previous page page_209 next page >

Page 209

Exercises 9.3

1. Let A=

(Q, A, q

, δ, F)

and B=

(S, A, s

, γ, G)

be automata. Let

θ: A

→

be an isomorphism. Prove

that the transition monoids

(A) and

(B) are isomorphic.

9.4 The syntactic monoid of a language

In this section, we shall show how to construct a monoid from

any

language. This monoid is finite if and

only if the language is recognisable, in which case it is isomorphic to the transition monoid of the

minimal automaton of the language.

Theorem 9.4.1

Let L be a recognisable language, whose minimal automaton is

with set of states S

Let be the function taking x to the function it induces on S. Then the kernel of is

given by the following:

if and only if for all we have that

Proof Let A=

(S, A, i, δ, T)

. Suppose that satisfy the condition that

for all

. We prove that . Let be an arbitrary state. We have to show that

We shall do this by proving that

and

are indistinguishable. Equality of

and

will then follow

from the fact that A is minimal and so reduced. By assumption, A is minimal and so accessible. It

follows that there exists such that

. Suppose that . Then and so

. By assumption, . Thus and so . We have shown that

The reverse implication can be proved similarly. We have therefore proved that . Hence

Now suppose that . By definition this means that . For any we have that

Suppose that . Then . But and so

(uxv)

(uyv)

. Hence , and

. We have proved that

< previous page page_209 next page >

< previous page page_210 next page >

Page 210

The reverse implication is proved similarly.

The above theorem motivates the following definition. Let

be an

arbitrary

language over the alphabet

. Define the relation

σL

* by if and only if

for all . Using this definition, we see that Theorem 9.4.1 says that when

recognisable. The following is left as an exercise.

Proposition 9.4.2

Let L be a language over the alphabet A. The relation σL is a congruence on A

with

the property that L is a union of some of the σL-classes

Let

be a language over the alphabet

. We call

σL

the

syntactic congruence of L

. The monoid

M(L)

σL

is called the

syntactic monoid

The definition of the syntactic congruence can be rendered more intuitive. One of the features of natural

languages is that words can be assigned to different grammatical categories, where words belonging to

the same category behave in the same way in the language. For example, in English we classify words

as being nouns, verbs, adjectives, adverbs, and so forth. To a first approximation a word is recognised

as a noun if it occurs in the same sorts of places in sentences as other nouns; likewise for verbs,

adjectives, etc. Let

be a language and let . A

context

for

is a pair of strings

such that . The set of all contexts of

is denoted by

C(x)

. Using this notation, we see that

means precisely that

C(x)

C(y)

. In other words,

and

occur as factors of elements of

exactly the same places. In terms of natural languages,

and

belong to the same ‘grammatical

category.’

Theorem 9.4.3

Let L be any language over the alphabet A. The syntactic monoid of L is finite if and

only if L is recognisable. If L is recognisable then the syntactic monoid is isomorphic to the transition

monoid of the minimal automaton for L.

Proof Suppose that

is recognisable with minimal automaton A. By Theorem 9.4.1, the kernel of is

σL

. Thus

σL

is the same as

*/=, and so by Theorem 9.3.1, the monoid

σL

is isomorphic to the

transition monoid of A. In particular,

σL

is finite.

Suppose that

σL

is finite. We prove that

is recognisable. Put

σL

and denote the

σL

congruence class containing

[x]

. Put

[ε]

and . Let . Define

[x]

[xa]

. This

is well-defined, because if then because

σL

is a congruence. Thus the definition

[x]

is independent of the choice of

. It follows that

< previous page page_210 next page >

< previous page page_211 next page >

Page 211

(Q, A, i,

·,

is a well-defined automaton. It is easy to check that if

is an arbitrary string in

* and

[x]

an arbitrary state in

then

[x]

[xu]

. To calculate

(A), observe that if and only if

. That is . But

is a union of

σL

-classes and so if and only if . It

follows that if and only if . Hence we have proved that

(A)=

and so

is recognisable.

It is worth stating explicitly how to calculate the syntactic monoid of a recognisable language.

Algorithm 9.4.4 Let

be a recognisable language. If

L(r),

where

is a regular expression, then we

can find the minimal automaton A of

using the Method of Quotients. Alternatively, if

(B) where B

is an automaton, then we can replace B by A=B

, which is again the minimal automaton for

. In

either case, we can then calculate the transition monoid of A using either Algorithm 8.2.2, thereby

obtaining explicitly the set of all functions induced by input strings to A, or Algorithms 8.2.4 and 8.2.5,

thereby obtaining an isomorphic copy of the transition monoid in terms of the monoid of

representatives. In either case, the monoid obtained is isomorphic to the syntactic monoid.

Describing the syntactic monoid of a recognisable language by means of a Cayley table is only practical

when it has a small number of elements. In general, the monoid is better described by means of its

representatives and relations.

Example 9.4.5 Let

)*. It is easy to check that the minimal automaton for

is the machine A

below.

< previous page page_211 next page >

< previous page page_212 next page >

Page 212

The table of representatives is

The set of relations is

(1)

aba

(9)

(2)

bab

(10)

(3)

3 (11)

(4)

3 (12)

(5)

3 (13)

(6)

2 (14)

(7)

3 (15)

(8)

3 (16)

Many of these relations are either superfluous or can be simplified using the fact that = is a congruence.

Relations (4), (5) and (8) tell us that

3 is the zero for the semigroup. I shall signal this by writing

3=0

and removing relations (4), (5) and (8). Relation (3) tells us that

3=0. The relations (7), (12) and (15)

are now superfluous. Notice that (6) follows from (1), because

a(aba)

;

and (10) follows from

(2), because

b(bab)

2. Relation (14) follows from (2), because

ab(bab)

;

and

relation (16) follows from (9) and (2), because

We therefore end up with the following set of relations:

(1)

3=0=

(2)

aba

(3)

bab

< previous page page_212 next page >

< previous page page_213 next page >

Page 213

(4)

(5)

(6)

These provide a more succinct description of the syntactic monoid of

as against the Cayley table,

which has 152=225 entries.

Exercises 9.4

1. Prove Proposition 9.4.2.

2. Compute the Cayley tables of the syntactic monoids of the following recognisable languages over

{a, b}

. Use as congruence representatives the strings arising from Algorithm 8.2.4.

(i) (

)*.

(ii) (

)+.

(iii)

(ab)

(iv)

)

(v)

aba.

(vi) (

(

)*.

(vii) (

aba

(

)*.

(viii)

ababa.

9.5 Summary of Chapter 9

•

Semigroup theory:

Semigroups and monoids form the algebraic component of automata theory.

Fundamental ideas concerned with semigroups are: subsemigroups, homomorphisms, and isomorphisms.

Each homomorphism of a semigroup is associated with a congruence and the image of the

homomorphism is isomorphic to the quotient or factor semigroup constructed from the congruence.

•

The syntactic monoid:

With each language we can construct a monoid, called the syntactic monoid.

This monoid is finite if and only if the language is recognisable. In this case, the syntactic monoid is

isomorphic to the transition monoid of the minimal automaton of the language.

< previous page page_213 next page >

< previous page page_214 next page >

Page 214

9.6 Remarks on Chapter 9

Theorem 9.2.11 is the ‘First Isomorphism Theorem’. There are two others in common use. The

Second

Isomorphism Theorem

runs as follows: let

be a congruence on a semigroup

and let

be a

subsemigroup of

. Then

ρ′

(T×T)

is a congruence on

so we can form the quotient semigroup

′

. On the other hand,

is a subsemigroup of

containing

. Observe that if and

aρb,

then . We can therefore form

the quotient semigroup

T′

. The Second Isomorphism Theorem states that

ρ′

is isomorphic to

T′

The

Third Isomorphism Theorem

is essentially Proposition 9.2.12: since

is a homomorphic image of

there is a congruence, say, such that is isomorphic to

. The congruence is usually

denoted .

Our characterisation in Theorem 9.4.3 of recognisable languages in terms of the syntactic congruence is

the one most useful to us, but many books give another characterisation, which is worth describing

here. Let A=

(Q, A, i, δ, T)

be an

accessible

automaton. Define the relation

* by iff

. It is easy to check that

A is an equivalence relation on

where each equivalence class is of

the form for some . In addition,

A is a right congruence, in the sense of

Question 4 of Exercises 9.2, and if then iff . We now use these properties as the

basis of a definition. A

Myhill-Nerode relation for the language

is any right congruence on

with the property that if

then iff . Thus

A is a Myhill-Nerode relation with a finite

number of right congruence classes. Now let

be an arbitrary language. Define

ρL

* by

iff for all . Then it can be checked that

ρL

is a Myhill-Nerode relation for

and that if

is any Myhill-Nerode relation for

then .

The Myhill-Nerode Theorem states that the following are equivalent:

(i) A language

over the alphabet

is recognisable.

(ii) There is a Myhill-Nerode relation for

with finitely many right congruence classes.

(iii) The relation

ρL

has only finitely many right congruence classes.

I shall sketch the proof.

(i) (ii). If

is recognisable, then it is recognised by some accessible automaton A. From the above,

A is a Myhill-Nerode relation for

with finitely many right congruence classes.

(ii) (iii). If

is some Myhill-Nerode relation for

with finitely many right congruence classes, then

from

we deduce that

ρL

has only finitely many right congruence classes.

< previous page page_214 next page >

< previous page page_215 next page >

Page 215

(iii) (i). From the relation

ρL,

we can construct an accessible automaton

whose states are the right

congruence classes and so, by assumption, there really are only finitely many states.

The details can be found in Lectures 15 and 16 of [75]. According to [65], the proof of this result is due

to Nerode [98], with Myhill [97] being responsible for that part of Theorem 9.4.3 that states that the

syntactic congruence of a language has only finitely many congruence classes if and only if the language

in question is recognisable.

The right congruence

ρL,

and the congruenee

σL

are special cases of the ‘principal congruences’ (see

page 175 of [77]) that can be defined for any subset

of any semigroup

see Proposition 10.3.2, for

example.

The syntactic monoid of a language surfaced first in [114] and their theory was systematically worked

out in [87].

< previous page page_215 next page >

< previous page page_216 next page >

Page 216

This page intentionally left blank.

< previous page page_216 next page >