Лабораторный практикум - Математические методы и модели в расчётах на ЭВМ

Подождите немного. Документ загружается.

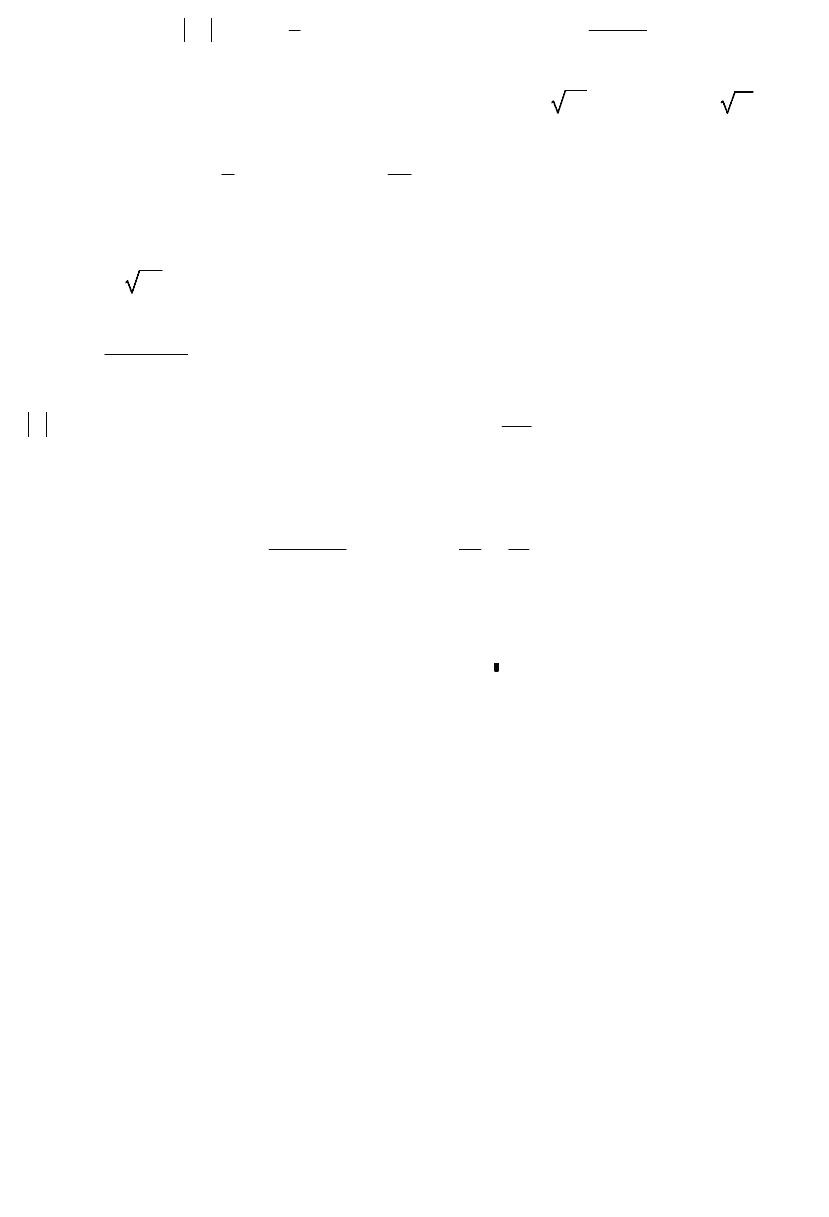
град 19.481 0.34

180



радarg z( ) 0.34z 95.769

Im z( ) 31.9Re z( ) 90.3z 90.3 31.9iz z1

z1 z2( )

z3















z3 10 9 iz2 7 6 iz1 4 i 5i 1i

Îïåðàöèè ñ êîìïëåêñíûìè ÷èñëàìè

sin















1tan















1cos ( ) 1

10 2.15410 3.1623

27e

54.598log 10( ) 1ln e( ) 1

4 2( )

2.5 2.8337 5.04 10



0.4444 42 10 4 4

С помощью панели Symbolic и оператора Complex можно

преобразовывать комплексные числа:

4 7 i( )

5 2 i

complex

6

1i

Для получения сопряжённого комплексного числа необходимо нажать

клавишу < ” > после ввода исходного комплексного числа:

5 7 i( )



5 7i

При помощи панели Calculus и вычислительных операторов можно

проводить операции дифференцирования, интегрирования, суммирования и

вычисления произведения:





15





120

Для ввода и написания функций, определённых пользователем, лучше

пользоваться клавиатурой, для ввода встроенных функций – как

клавиатурой, так и инструментарием. Для определения функции

пользователя необходимо ввести имя функции, в скобках через запятую

ввести имена переменных, ввести оператор присваивания и в появившийся

местозаполнитель ввести выражение, определяющее функцию. Например,

необходимо вычислить функцию

yxyxyxf *),(



при х=5, у=10. Ниже приведён результат ввода:

f x y( ) x

 x y x 5 y 10 f x y( ) 175 f 5 10( ) 175

В Mathcad предусмотрены операторы, позволяющие строить

двухмерные (декартовые и полярные) и трёхмерные (поверхности, линии

уровня, гистограммы, множество точек и векторное поле) графики. Все они

создаются с помощью панели инструментов Graph (выбор соответствующей

пиктограммы), либо путём выбора соответствующего элемента подменю

Insert → Graph→ Вставка. В результате в обозначенном месте появляется

пустая область графика. Далее в местозаполнители необходимо ввести имена

переменных или функции и аргумента, которые должны быть изображены

графически. Для построения графика в декартовой системе координат

предварительно необходимо сформировать два вектора данных или ввести

функцию:

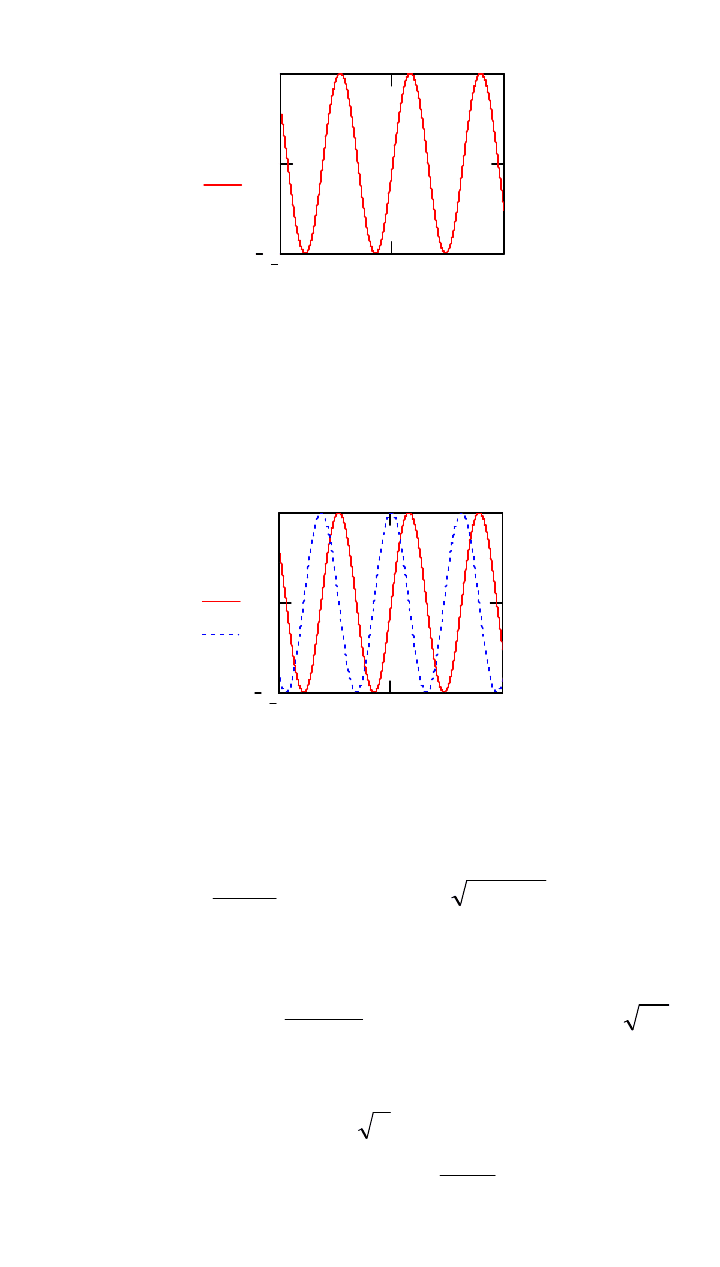
f1 t( ) sin t( )

10 0 10

f1 t( )

По умолчанию график строится в диапазоне аргумента от -10 до +10.

На одном графике можно построить до 16 различных зависимостей,

для чего используется клавиша < , > для введения названия другой функции

этого же аргумента или другого:

f1 t( ) sin t( ) f2 x( ) cos x( )

10 0 10

f1 t( )

f2 x( )

t x

При редактировании графиков можно менять диапазон и масштаб осей.

Порядок выполнения работы

1. Выполнить следующие математические операции:

.);143ln();10/tan();sin();cos(

;;9;8;

710

)10(4

127log

efbxay

bacba











2. Вычислить

.3103;742;651

;1);5arg();4Im();5Re(;

3*2

15;3214

iziziz

еслиzzzz

zzzzzz







3. Определить значение функций

.8,

4,2)10ln()cos()(

;34;9,5xy)f(x,











tttf

yxyxy

4. Построить графики функций

).cos()sin()(;210)(;351)(

tttfttftttf 

Вопросы для самопроверки

Почему пакет Mathcad называют мощным калькулятором?

Для чего служат панели инструментов Mathcad?

Перечислите пункты главного меню пакета Mathcad.

Приведите примеры встроенных функций и операторов пакета

Mathcad.

Опишите процедуру построения двухмерного графика. Как можно

построить несколько графиков разных аргументов? Как редактируются

графики?

Что такое оптимизация программ?

Литература

Макаров Е.Г. Инженерные расчёты в Mathcad. Учебный курс. – Спб.:

Питер, 2003. – 448с.: ил.

Гурский Д.А. Вычисления в MathCAD / Д.А. Гурский. – Мн.: Новое

знание, 2003. – 814с.: ил.

Кирьянов Д.В. Самоучитель Mathcad 12. – СПб.: БХВ-Петербург, 2004.

– 576с.: ил.

Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad. –

СПб.: БХВ-Петербург, 2005. – 464с.: ил.

Алексеев Е.Р., Чеснокова О.В. Решение задач вычислительной

математики в пакетах Mathcad 12, MATLAB 7, Maple 9 / Алексеев Е.Р.,

Чеснокова О.В. – M.: НТ Пресс, 2006. – 496с.: ил. – (Самоучитель).

Лабораторная работа № 2 - 2

Алгебраические уравнения и линейная алгебра

Цель работы: выработать навыки использования различных программ

для решения алгебраических уравнений и дать представления о

возможностях пакета при выполнении действий над матрицами.

Введение

В пакете Mathcad матричные вычисления реализованы в виде

операторов, написание которых по смыслу максимально приближено к их

математическому смыслу. Матрицы должны иметь соответствующие

размерности.

Для ввода матрицы необходимо использовать математическую панель

Matrix. Простейшие действия с матрицами рассмотрим на примерах:

invA

0.857

0.4

0.886

0.429

0.143

0.2

0.086













invA A

1



geninv A( )

0.857

0.4

0.886

0.429

0.143

0.2

0.086















detA 35detA AM













M A QQ















tr A( ) 14F













F D 2D













D C 10

1

3

1













C A BB













B A

A















Матрицы определённого вида создаются с помощью следующих

встроенных функций:

identity 3( )













 G













 diag G( )















Отдельные части матрицы выделяются с помощью операторов:

1 2

8 A

 













 submatrix A 0 1 1 2( )















Характеристики матриц можно получить с помощью следующих

встроенных функций:

rows A( ) 3 cols A( ) 3 rank A( ) 3

cond1 A( ) 38.571 cond2 A( ) 21.975 conde A( ) 23.079 condi A( ) 28.571

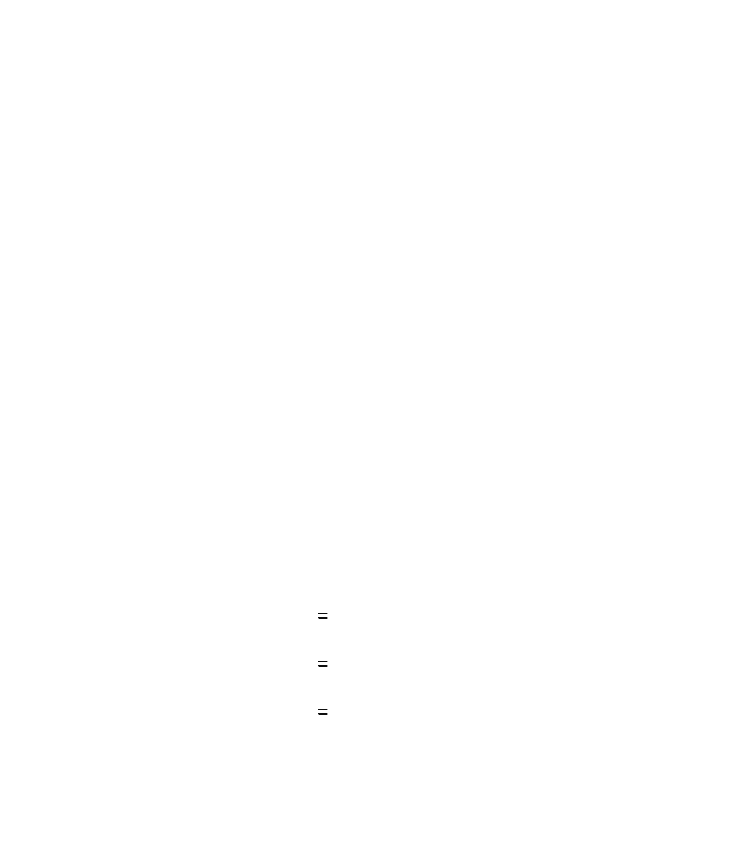
Последние встроенные функции позволяют вычислять числа

обусловленности (condition number) квадратной матрицы в норме L1, L2, в

евклидовой норме и в ∞ - норме. Число обусловленности связано с нормой

матрицы:

norm1 A( ) 18 norm2 A( ) 16.247 norme A( ) 16.523 normi A( ) 20

Анализ линейных электрических цепей постоянного и переменного

тока связан с решением систем линейных алгебраических уравнений,

которые в матричной форме записываются как

;

ERI





где G, R – квадратные матрицы узловых проводимостей и контурных

сопротивлений; φ, I, J, E – вектор - столбцы узловых потенциалов, контурных

токов, узловых токов и контурных ЭДС. В Mathcad такие системы можно

решать с помощью встроенной функции lsolve(…) или встроенного блока

Given - Find:

20

10

20

23

10

23













 E

54













 lsolve R E( )

0.14

0.86

0.018















I11 0 I22 0 I33 0

Given

40 I11 20 I22 10 I33 23

20 I11 60 I22 23 I33 54

10 I11 23 I22 75 I33 17

find I11 I22 I33( )

0.14

0.86

0.018















Первый алгоритм – метод Гаусса, второй – линейный численный

алгоритм.

При анализе и синтезе систем управления возникает задача поиска

собственных векторов и собственных чисел квадратной матрицы А, которую

называют матрицей состояния. Собственные числа матрицы А являются

корнями характеристического уравнения системы управления. Для решения

таких задач в Mathcad встроены функции [3]:

- eigenvals(A) – вычисляет вектор собственных значений матрицы А;

- eigenvecs(A) – вычисляет матрицу, содержащую нормированные

собственные векторы, соответствующие собственным значениям матрицы А;

n-й столбец вычисляемой матрицы соответствует собственному вектору n-го

собственного значения, вычисляемого eigenvals(A);

- eigenvec(A,p) – вычисляет собственный вектор для матрицы А и заданного

собственного значения р.

Листинг применения этих функций представлен ниже:













 A 210 eigenvals A( )

15.91

3.545 0.795i

3.545 0.795i















eigenvecs A( )

0.213

0.91

0.354

0.807

0.371 0.334i

0.201 0.244i

0.807

0.371 0.334i

0.201 0.244i















eigenvec A 15.91( )

0.213

0.91

0.354















Характеристическое полином системы определяется матричным

уравнением

),*det()( AIppF 

где I – единичная матрица, р – переменная. Это функция переменной р и её

необходимо упростить с помощью математической панели Symbolic →

simplify:













 I















F p( ) p I A simplify p

23 p

 126 p 210

Полученное выражение является полиномом и его корни определяются

с помощью функции polyroots(a), где а – вектор коэффициентов полинома.

Первым в векторе должен идти свободный член полинома:

210

126

23













 polyroots a( )

3.545 0.795i

3.545 0.795i

15.91















Корни полинома и собственные числа матрица А совпадают.

Для функции polyroots(a) предусмотрены два численных метода –

метод полиномов Лаггера (установлен по умолчанию) и метод парной

матрицы. Для смены метода необходимо вызвать меню, нажав правую мышь

на слове polyroots и выбрать соответствующий метод.

Порядок выполнения работы

1. Введите матрицы

1000

0100

0010

0001

;

25735

21919

58123

94510









































 IBA

2. Выполните следующие математические операции: C = B

; D = A*B;

Q = A-10; trA; detA.

3. Для матрицы А определить её характеристики, собственные числа и

числа обусловленности.

4. Решить систему линейных алгебраических уравнений

.105376221117

;60321245110

;78317210150







xxx

5. Решить матричное уравнение

.0)*det(  AIp

Вопросы для самопроверки

Дайте определение матрицы и приведите примеры единичной и

диагональной матриц.

Какие операции можно проводить с матрицами?

Что такое вырожденная и невырожденная матрицы?

Какие методы реализованы в Mathcad для решения СЛАУ?

Как рассчитываются собственные числа матриц?

Литература

Макаров Е.Г. Инженерные расчёты в Mathcad. Учебный курс. – Спб.:

Питер, 2003. – 448с.: ил.

Гурский Д.А. Вычисления в MathCAD / Д.А. Гурский. – Мн.: Новое

знание, 2003. – 814с.: ил.

Кирьянов Д.В. Самоучитель Mathcad 12. – СПб.: БХВ-Петербург, 2004.

– 576с.: ил.

Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad. –

СПб.: БХВ-Петербург, 2005. – 464с.: ил.

Алексеев Е.Р., Чеснокова О.В. Решение задач вычислительной

математики в пакетах Mathcad 12, MATLAB 7, Maple 9 / Алексеев Е.Р.,

Чеснокова О.В. – M.: НТ Пресс, 2006. – 496с.: ил. – (Самоучитель).

Лабораторная работа № 2 - 3

Решение обыкновенных дифференциальных уравнений в Mathcad

Цель работы: закрепить знания о применении дифференциальных

уравнений для анализа временных характеристик электрических цепей и

систем управления; развить навыки и умения решать дифференциальные

уравнения.

Введение

Дифференциальные уравнения – это уравнения, в которых

неизвестными являются функции. Обыкновенное дифференциальное

уравнение имеет единственное решение, если заданы начальные или

граничные условия. Решить дифференциальное уравнение – значит

определить неизвестную функцию на определённом интервале изменения её

аргумента (в нашем случае это время t). Для численного интегрирования

одного обыкновенного дифференциального уравнения n порядка можно

использовать блок Given / Odesolve или встроенные функции.

Применение блока Given / Odesolve для решения уравнений первого

порядка реализуется в три этапа:

- Given

- ввод дифференциального уравнения, разрешённого относительно первой

производной, и начального условия с помощью логических операторов;

- Odesolve(t,t1), где t1 - конечное время;

- построение графика функции.

Имеется возможность выбирать метод решения – метод Рунге-Кутты с

фиксированным шагом (по умолчанию) и адаптивный. Для этого нажатием

правой мыши на области функции Odesolve вызывается контекстное меню и

выбирается один из пунктов: Fixed или Adaptive.

Рассмотрим решение дифференциального уравнения первого порядка

.0)0(,1000100  ii

Данное уравнение имеет точное аналитическое решение

).100exp(1010)( tti 

и численное решение, полученное с помощью блока Given / Odesolve, легко

можно проверить. Непосредственное применение этого блока дает

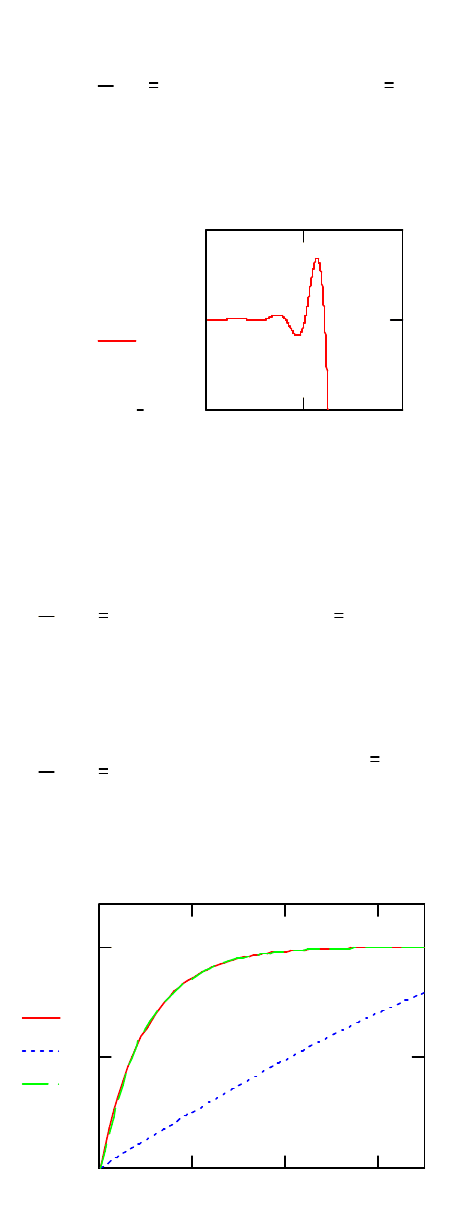
неудовлетворительный результат (метод Рунге – Кутты с фиксированным

шагом, рис. 1; адаптивный, кривая i1, рис. 2).

Для точного решения целесообразно применять функцию

Odesolve(t,t1,m), где m – число шагов интегрирования на интервале решения.

Пример применения этой функции приведён на рис. 2 (кривая i2). Здесь же

показано точное аналитическое решение (кривая ir). Очевидно, что получен

хороший результат.

Аналогично можно решать дифференциальные уравнения порядка

выше первого. Начальные условия задаются на функцию и её производные

до n-1 порядка включительно.

Given

i t( )

100 i t( ) 1000 i 0( ) 0

i Odesolve t 0.7( )

0 0.5 1



i t( )

Рис. 1

ir t( ) 10 10 e

100 t

 t 0 0.001 0.7

Given

i1 t( )

100 i1 t( ) 1000 i1 0( ) 0

i1 Odesolve t 0.7( )

Given

i2 0( ) 0

i2 t( )

100 i2 t( ) 1000

i2 Odesolve t 0.7 100( )

0 0.02 0.04 0.06

ir t( )

i1 t( )

i2 t( )

Рис. 2

Для решения дифференциальных уравнений первого порядка и систем

дифференциальных уравнений первого порядка в Mathcad предусмотрены

три встроенные функции, обращение к которым выполняется одинаково:

- rkfixed(y0,t0,tk,m,D) – метод Рунге-Кутты четвёртого порядка с

фиксированным шагом;

-Rkadapt(…) – метод Рунге-Кутты четвёртого порядка с переменным шагом;

-Bulstoer(…) - метод Булирша-Штера, целесообразно применять, если

известно, что решение является гладкой функцией. Здесь у0 – вектор

начальных условий в точке t0 размерностью n×1; t0 – начальное время; tk –

конечное время; m – число шагов на интервале решения; D – векторная

функция двух переменных, у и t. Результат расчёта выдается в виде матрицы

размерностью m×2: первый столбец – аргумент, второй – значение функции .

Эту особенность необходимо учитывать при построении графиков, ибо в

качестве переменных рассматриваются величины u1

(функция) и u1

(аргумент). Верхний индекс должен указываться с помощью панели Matrix

→M

< >

, т.е. u1

<1>

и u1

<0>

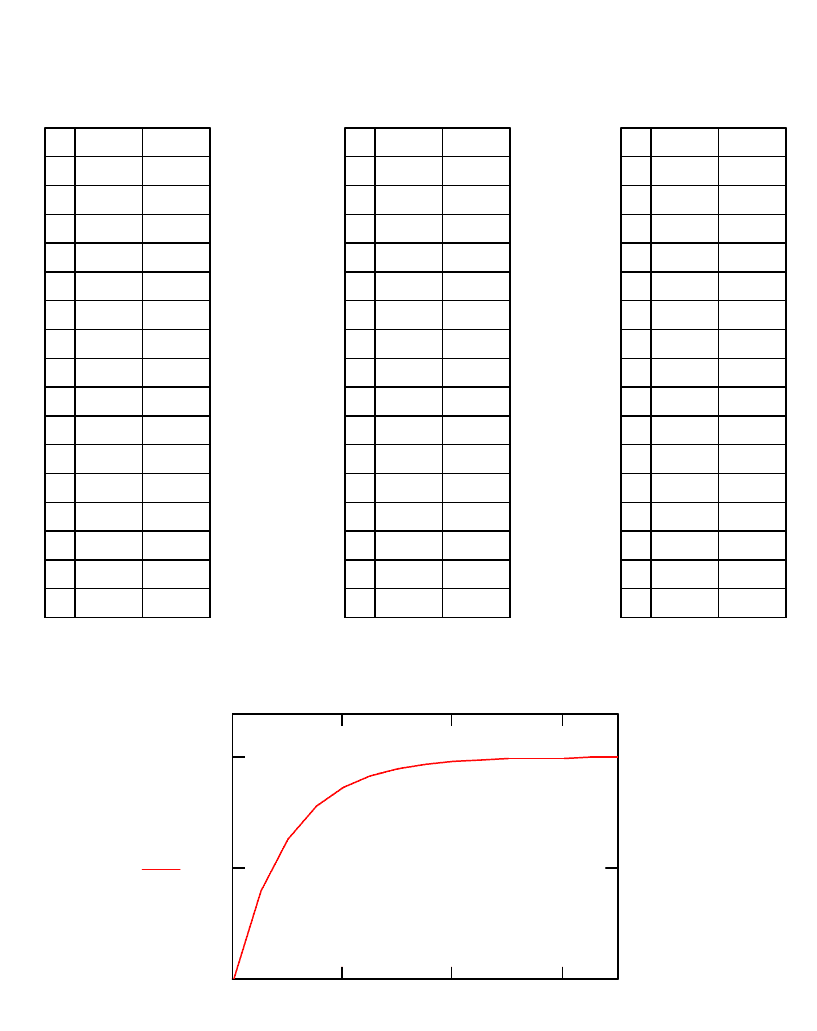
Пример расчёта приведён на рис. 3.

D t i( ) 100 i 1000 i0 0 t0 0 tk 0.5 m 100

u1 rkfixedi0 t0 tk m D( ) u2 Bulstoer i0 t0 tk m D( ) u3 Rkadapt i0 t0 tk m D( )

0 1

0 0

5·10

-3

3.932

0.01 6.318

0.015 7.766

0.02 8.645

0.025 9.178

0.03 9.501

0.035 9.697

0.04 9.816

0.045 9.889

0.05 9.932

0.055 9.959

0.06 9.975

0.065 9.985

0.07 9.991

0.075 9.994

 u2

0 1

0 0

5·10

-3

3.935

0.01 6.321

0.015 7.769

0.02 8.647

0.025 9.179

0.03 9.502

0.035 9.698

0.04 9.817

0.045 9.889

0.05 9.933

0.055 9.959

0.06 9.975

0.065 9.985

0.07 9.991

0.075 9.994

 u3

0 1

0 0

5·10

-3

3.935

0.01 6.321

0.015 7.769

0.02 8.647

0.025 9.179

0.03 9.502

0.035 9.698

0.04 9.817

0.045 9.889

0.05 9.933

0.055 9.959

0.06 9.975

0.065 9.985

0.07 9.991

0.075 9.994



0 0.02 0.04 0.06

 

Рис. 3