Лабораторные работы по курсу общей физики (2-я Редакция 2012 г.)
Подождите немного. Документ загружается.

2
Если М
тр
=const, нить нерастяжима и нет проскальзывания между нитью и
шкивом, то движение системы тел можно считать равноускоренным. Для
равноускоренного движения справедливы следующие соотношения:
V
2
= 2a x , ω
2
= 2ε α. (3)
Разделив (2) на α, получаем с учетом выражения (3)
mg r = Iε + ma r + M
тр
, (4)
где r – радиус шкива.
Заменяя a = ε r, определим момент инерции маятника
2
mr
Mmgr
I
тр
−
−
=
ε
(5)
Для равноускоренного движения (см. дабораторную работу №3)
2
4
Dt
x
=ε
(6)
Преобразуем (5) с учетом (6)
4
2
2
D
mKtI −=
,
где
x
DM
D
mg
K
тр
4
)
2
( −
=
(7)
Значение K указано в паспорте установки.
Для нашей установки
4
2
D
mI >>
. Это эквивалентно выполнению
следующих неравенств: (Iω
2
/2) >> (mV
2
/2), mgx >> max, g>> a, (gt
2
/2)>> (at
2
/2)
= x.
Для расчетов представим момент инерции в окончательном виде
I = K t
2
(8)
Для определения момента инерции маятника необходимо измерить время
прохождения грузом m расстояния x (см. рисунок в лабораторной работе
№3).
3
Задания
1. Закрепив тела на равных расстояниях от оси вращения, измерьте это
расстояние (R).
2. Намотав нить на шкив большого диаметра,, произведите трехкратное
измерение времени опускания груза t.
3. Повторите опыт при четырех различных расстояниях закрепляемых тел от
оси вращения.
4. Вычислите моменты инерции маятника для всех измерений 2 и 3.
5. Рассчитайте оценки стандартных отклонений для всех полученных
значений момента инерции.
6. Постройте график зависимости момента инерции от расстояния масс до
оси вращения в координатах I, R
2
с учетом вычисленных оценок стандартных
отклонений.
Контрольные вопросы
1. Какова цель данной работы?
2. Что называется моментом инерции тела?
3. При каких допущениях получена формула (1)? Что необходимо учесть
при проведении эксперимента, чтобы эта формула была справедлива?
4. При каких допущениях движение маятника и груза можно считать
равноускоренным?
5. При каких допущениях получена формула (8)?
6. Как измерить расстояния от оси вращения до центра массы тела,
закрепленного на стержне?
7. Как рассчитать оценку стандартного отклонения момента инерции
маятника Обербека?
8. В каких осях следует построить зависимость момента инерции от
расстояния грузов до оси вращения, чтобы выяснить, подтвердилась ли
теоретическая зависимость (1)?
9. Выполняются ли неравенства, приведенные в работе?
Рекомендуемая литература
1. Савельев И. Н. Курс общей физики. – М.: Наука, 1989. – Т. 1, § 31-33.
2. Ландау Л. Д., Ахиезер А. И., Лифшиц Е. М. Курс общей физики. – М.:
Наука, 1969. - § 25, 28.
1
Лабораторная работа № 5
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ МЕТОДОМ
КЛЕМАНА И ДЕЗОРМА
В данной работе определяется отношение теплоемкостей при постоянном
давлении и постоянном объеме С
р
/С
v
≡ g для воздуха. Полученное значение g
сравнивается с теоретическим.
Обсуждение методики работы.
Одним из самых простых и остроумных методов определения g
является метод Клемана и Дезорма, основанный на использовании
адиабатического процесса. Уравнение адиабаты для идеального газа
PV
g
=const позволяет при известных давлении и объеме некоторой массы газа
в двух состояниях вычислить g. Для выполнения адиабатического процесса
можно поместить газ в термоизолированный сосуд и в нем производить
адиабатическое сжатие или расширение газа.
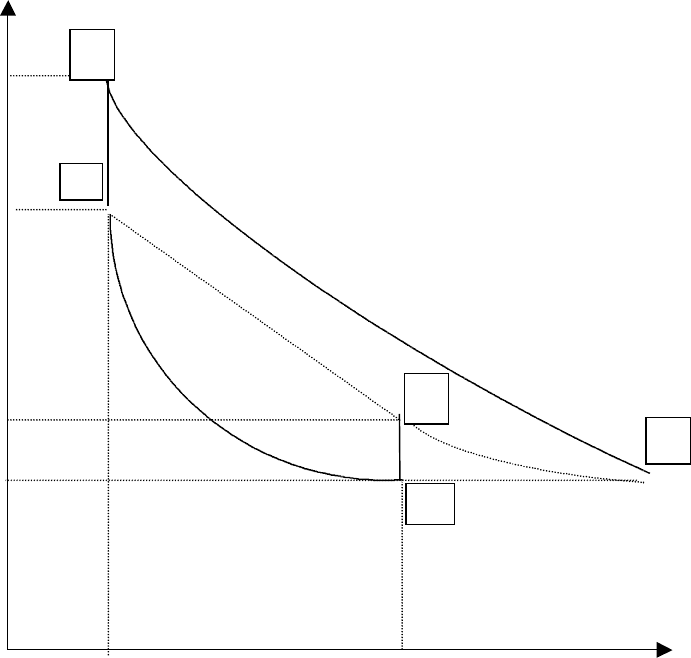
Изобразим графически в координатах P, v (где v = V/m – объем
приходящийся на единицу массы газа) основные процессы, используемые в
работе для определения g (Рис.1).
P
P
1
P
2
P
4
P
3
V
1
V
2
V
Рис.1
1
2
0
3
4

2
1. Кривая 0-1 соответствует накачиванию воздуха в баллон. Давление при
этом увеличивается а удельный объем уменьшается. Относительно
температуры в точке 1 можно только сказать, что она не ниже комнатной.
2. Как только накачивание прекращаем и сохраняем неизменный объем,
давление в баллоне начинает падать (так и происходит на опыте). При
постоянном объеме уменьшение давления сопровождается понижением
температуры. Значит в точке 1 температура оказалась выше комнатной, и на
участке 1-2 она снижается за счет контакта с окружающей средой до
комнатной.
3. Когда давление перестает изменяться (точка 2), резко выпускаем воздух из
баллона. Будем считать, что это адиабатическое расширение 2-3. В
результате объем рассматриваемой массы газа увеличивается от V
2
до V
3
,
температура должна понизиться.
4. Снова объем газа выдерживаем постоянным – изохорический процесс на
участке 3-4. На опыте обнаруживается, что давление при этом повышается,
следовательно, повышается и температура. Это значит .что в точке 3
температура действительно была ниже комнатной и теперь она повышается
до комнатной за счет контакта с окружающей средой.
В точках 0, 4, 2 газ имеет одинаковую температуру – комнатную, т.е.
мысленно мы эти точки можем уложить в на гипотетическую изотерму 0-4-2.
Это обстоятельство позволило Клеману и Дезорму обойтись без измерения
начального и конечного объема газа. Имеено в этом и сказалось остроумие
предложенного метода.
Для точек 2 и 3, лежащих на одной адиабате, можно записать (рис. 1).
P
2
V
2
γ
= P
3
V
3
γ
(1)
Для точек 2 и 4, лежащих на одной мысленно проведенной изотерме, можно
записать (рис. 1)
P
2
V
2
=P
4
V
4
(2)
Кроме того, прямая 3-4 изображает изохорический процесс, т.е.
V
3
=V
4
(3)
Решая систему (1)-(3), получим уравнение для нахождения γ. В него, кроме
давлений, которые легко измеряются манометром, больше ничего не входит
2
3
2
4
P
P
P
P
=
γ
(4)
3
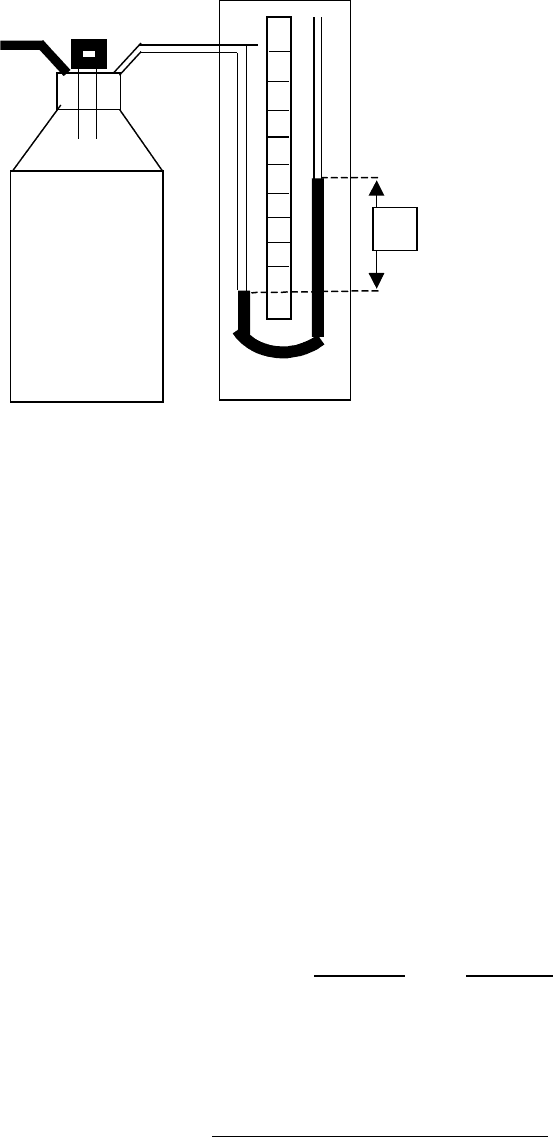
Описание экспериментальной установки
Сказанное выше и определяет все
особенности экспериментальной
установки. Она состоит из стеклянного
сосуда, закрытого проб кой, в которую
вмонтированы две трубки и
быстродействующий клапан для
выпускания воздуха из сосуда (рис. 2).
Одна трубка соединяет полость сосуда
с манометром. Манометром служит U-
образная трубка, наполненная
подкрашенной жидкостью. Давление
измеряется по разности уровней в
коленах трубки. Вторая трубка через
клапан соединяет полость баллона с
насосом.
Рис.2
Измерение
Величина P
2
= P
0
+ h
1
, где P
0
- атмосферное давление, h
1
- разность между
атмосферным давлением и давлением воздуха в баллоне после накачивания
воздуха и охлаждения его до комнатной температуры (см. рис. 1, точка 2).
Аналогично, давление P
4
= P
0
+ h
2
, где h
2
– разность между атмосферным
давлением и давлением внутри баллона после адиабатического расширения и
нагревания воздуха в баллоне до комнатной температуры (см. рис. 1, точка
4). Давление Р
3
= Р
0
. Подставив эти значения в формулу (4), получим
10
0
10
20
hP
P
hP
hP
+
=
+
+
γ
Логарифмируя это уравнение, находим
)ln()ln(
)ln(ln
1020
100
hPhP
hPP
+−+
+
−
=γ
(5)
При условии, что P
0
>> h
1
и h
2
, для упрощения этой формулы используем
известное свойство логарифмов ln(1+x) ≅ x при. x<<1. Тогда
ln(P
0
+ h
1
) = lnP
0
(1+ h
1
/P
0
) ≅ lnP
0
+ h
1
/P
0
;
ln(P
0
+ h
2
) ≅ lnP
0
+ h
2
/P
0
;
h

4
(6)
21
1
hh
h
−
=γ
Таким образом эксперимент сводится к измерениям h
1
и h
2
.
Теоретическое значение γ.
Полученное экспериментальное значение γ сравниваем с теоретическим.
При этом, воздух в баллоне считаем идеальным газом двухатомных молекул,
связь атомов в молекулах принимаем жесткой. Расчет теоретического
значения γ при таких допущениях произведите самостоятельно.
Оценка стандартного отклонения величины γ
Величины h
1
и h
2
определяются по разностям уровней жидкости в U-
образной трубке манометра. Стандартное отклонение σ
γ
находим по формуле
переноса ошибок:
( )
h
hh
h
σσ
γ
2
21
1
2
−
=
(7)
Задания
1) Измерьте γ три раза.
2) Рассчитайте оценку стандартного отклонения величины γ.
3) Сравните экспериментальное и теоретическое значения γ.
Контрольные вопросы
1. Что Вы будете определять в данной работе? Что Вы ожидаете получить?
2. Что такое γ?
3. Что называется молярной теплоемкостью и почему она зависит от условий
нагревания?
4. Что называется удельной теплоемкостью и как она связана с молярной?
5. Какие изопроцессы используются для вывода расчетной формулы в
данной работе? Запишите уравнения этих процессов.
6. Какова связь между давлениями в точках 2, 3, 4 на диаграмме рис.1?
7. Как в полученном выражении (4) записать давления, зная показания
манометра и атмосферное давление?
8. При каких условиях ln(P
0
+ h) можно заменить на lnP
0
+ h/P
0
?
9. Как в данной работе Вы будете оценивать случайные отклонения
величины γ?
5
10. Согласуется ли полученное Вами значение γ с теоретическим? Что это
означает?
11. Выполняется ли в данной работе условие (h/P
0
) << 1? (Учтите, что h и P
0
должны быть выражены в одинаковых единицах).
Рекомендуемая литература
1. Савельев И. В. Курс общей физики. – М.: Наука, 1989. – Т. 1. - § 68, 69, 72.
2. Яворский Б. И. и др. Курс физики. – М.: Высшая школа, 1973. – Т. 1. - §
9.2, 10.1-10.5.
1. Кикоин И.К., Кикоин А.К. Молекулярная физика. – М.: Физмат, 1963. –
Гл. 2 - § 1-9.
Министерство образования Российской Федерации
Новосибирский государственный технический университет
МЕХАНИКА
И ТЕРМОДИНАМИКА
Лабораторный практикум по физике для студентов
1,2 курсов всех факультетов и форм обучения
Составители: В.Г.Дубровский, А.А.Корнилович,
И.И.Суханов, А.А.Харьков
Рецензент: В.Н.Холявко
Работа подготовлена на кафедре Прикладной и
теоретической физики
Новосибирск 2002
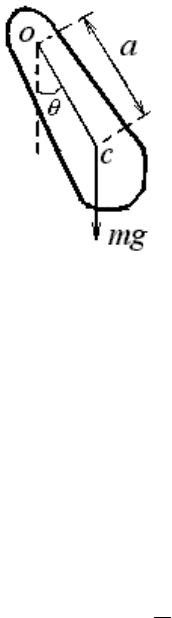
1
Лабораторная работа № 20 а
СВОБОДНЫЕ КОЛЕБАНИЯ ФИЗИЧЕСКОГО МАЯТНИКА
Цель работы – исследование зависимости периода колебаний
физического маятника от положения оси вращения, относительно которой
происходит качание маятника. Полученную зависимость использовать для
экспериментального определения момента инерции тела относительно оси,
проходящей через центр инерции, и относительно других осей ,параллельных
первой.
Дифференциальное уравнение колебаний физического маятника
Физический маятник - твердое тело, которое может вращаться под
действием своей силы тяжести
mg
вокруг неподвижной горизонтальной оси
o
, не проходящей через центр инерции
c
этого тела. Схема маятника
показана на рисунке 1.
Рис. 1
Дифференциальное уравнение колебаний (уравнение движения)
физического маятника можно получить из закона сохранения энергии. В
состоянии равновесия потенциальную энергию маятника будем считать
равной нулю. Тогда при отклонении маятника на угол
θ
потенциальная
энергия будет равна
).cos1(mgaЕ
п
θ
−
=
Кинетическая энергия маятника
2
к
I
2
1
Е θ
&
=
В этом выражении
I
- момент инерции маятника относительно оси вращения,
θ
&
- первая производная от угла поворота по времени ( угловая скорость ).
Полная механическая энергия маятника

2
)cos1(mgaI
2
1
ЕЕЕ
2
пк
θθ −+=+=
&
( 1 )
Если угол отклонения от положения равновесия
θ
мал, то
2
1cos
2
θ
θ −≈ .
Тогда выражение (1 ) можно переписать в виде
22
mga
2
1
I
2
1
Е θθ +=
&
( 2 )
Поскольку при колебаниях маятника неизбежно совершается работа по
преодолению сил трения, механическая энергия
Е
постепенно убывает.
Учитывая, что в дальнейшем нас будет интересовать прежде всего период
колебаний, предположим, что потери энергии за время одного периода по
сравнению с полной энергией пренебрежимо малы. Определим уравнение
движения , а из него и период колебаний, в этом приближении.
Если потерями энергии пренебречь, то
const
Е
=
, а
0
Е
=
&
. Определим
Е
&
из выражения ( 2 ) и приравняем эту производную нулю. В результате
получим выражение
0
I
mga
=+ θθ
&&
( 3 )
Решение дифференциального уравнения ( 3 ) имеет вид
)tcos(
0m
ϕ
ω
θ
θ
+
=
( 4 )
Здесь
m
θ
- амплитуда колебаний, )t(
0
ϕ
ω
+
- фаза колебаний,
ω
- круговая (
циклическая ) частота,
0
ϕ
- начальная фаза. Амплитуда колебаний и
начальная фаза из уравнения (3) не находятся. Они определяются заданием
так называемых начальных условий. Круговая частота колебаний
ω
определяется видом уравнения (3) и равна корню квадратному из
коэффициента перед переменной
θ
, т. е.
I
mga
=ω (5)
Период колебаний
Т
связан с
ω
соотношением
ω
π
2
T = . Учитывая ( 5 ),
получим выражение для периода колебаний
mga
I
2T π= ( 6 )
Колебания, описываемые выражением (4) называются гармоническими.
Уравнение (3) является дифференциальным уравнением гармонического
осциллятора (в нашем случае – физического маятника), записанным в
стандартной форме.
