Лабораторные работы по курсу общей физики (2-я Редакция 2012 г.)

8

гармоническое колебание, которое является результатом суперпозиции

двух нормальных колебаний с близкими частотами.

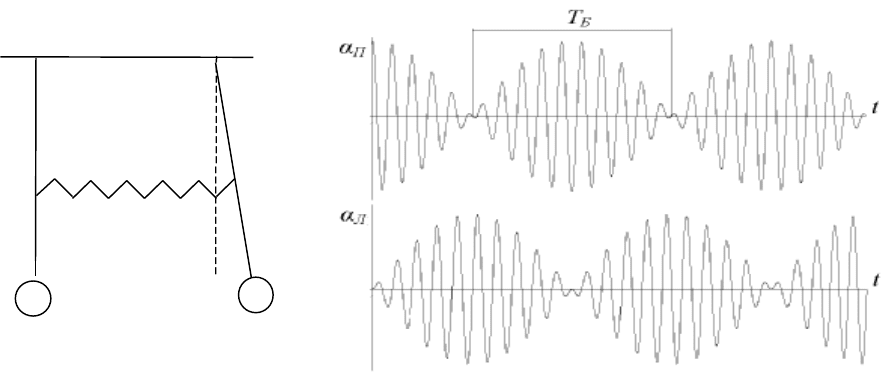
Рис. 5

На рис.5 показан характер движения маятников. Частоты биений обоих

маятников одинаковы и равны разности частот нормальных колебаний:

12

ωωω −=

Б

.

Период биений равен

)/(2/2

12

ωωπωπ

−

=

ББ

T

(31)

Таким образом, теоретическое рассмотрение процессов, происходящих в

экспериментальной установке, приводит к следующим выводам.

1) Первоначальное отклонение маятников в одну и ту же сторону на

равные углы возбуждает нормальные колебания первого (синфазного)

типа. При этом частота этого нормального колебания

1

ω совпадает с

частотой

0

ω колебаний одного отдельно взятого маятника

(изолированного от другого маятника) и не зависит от положения

пружины.

2) Первоначальное отклонение маятников в разные стороны на равные по

величине углы возбуждает нормальные колебания второго

(противофазного) типа. Частота этого нормального колебания

2

ω

больше частоты первого нормального колебания

1

ω . Увеличение

расстояния

r

от оси вращения до места закрепления пружины приводит

к возрастанию частоты

2

ω .

0

α

9

3) При первоначальном отклонении маятников на неравные углы

(например, в ситуации рис. 5) каждый из маятников совершает сложное

негармоническое движение, являющееся суперпозицией (суммой)

нормальных колебаний обоих типов. При слабой связи маятников при

этом наблюдается явление биений с частотой биений

Б

ω . С увеличением

расстояния

r

частота биений возрастает.

В настоящей работе проводится экспериментальная проверка этих

теоретических выводов.

Измерение частот колебаний.

В данной работе непосредственно измеряется время

N

t наблюдения

N

колебаний. Если

Т

- период колебаний, то

N

tNT /2/2 ππω == (32)

Таким образом, по измеренному времени

N

t можно рассчитать

соответствующую частоту колебаний

ω

(т.е.

0

ω ,

1

ω ,

2

ω ,

Б

ω ).

Погрешность

ω

σ измерений частот зависит от погрешности измерений

времени

N

колебаний. Чем больше число

N

, тем меньше

ω

σ . В задании к

работе даны рекомендованные значения

N

.

Формулу для расчета величины

ω

σ предлагается вывести самостоятельно.

Задание к лабораторной работе

В рассмотренной теоретической модели углы отклонения маятников от

положения равновесия полагались малыми (предположения (1) (2)),

поэтому при выполнении лабораторной работы следует иметь в виду, что

максимальные углы отклонения маятников должны быть не более,

например, 10 градусов.

В задании даны рекомендованные значения для чисел наблюдаемых

колебаний

N

(30, 10 и 5). Можно брать большие, чем рекомендованные,

значения величины

N

. При этом точность измерения частот возрастет.

1. Снять пружину. Измерить частоты

0

ω собственных колебаний каждого из

маятников по времени 30 колебаний. Если частоты маятников отличаются

друг от друга более чем на 1%, то их необходимо уравнять, перемещая

чечевицу одного из маятников по стержню (штанге).

2. Установить пружину в положение, при котором период биений в

несколько раз (например, в 5 раз) превышает период колебаний

маятников). Измерить частоты нормальных колебаний

1

ω и

2

ω по

10

времени 10 колебаний, возбуждая эти колебания в соответствии с рис. 3 и

4. Измерить при том же положении пружины частоту биений

Б

ω по

времени 5 биений, возбуждая их по схеме рис. 5. Проводя эти измерения,

наблюдайте за движением одного маятника. Отсчет времени начинайте с

положения, когда амплитуда колебания маятника равна нулю. Помните,

что период одного биения – это минимальный промежуток времени, через

который амплитуда колебания маятника снова станет равной нулю

(повторение состояния).

3. Выполнить пункт 2 задания еще для 4-х других положений пружины,

поднимая его вверх.

4. Вычислить частоту биений

Б

ω как разность частот нормальных

колебаний для всех 5-ти положений пружины.

5. Представить результаты измерений с учетом погрешностей измерений

графически в удобной для восприятия и сопоставления форме.

6. По результатам работы сделать выводы относительно справедливости

следующих теоретических предсказаний:

• о приближенном равенстве частоты

1

ω синфазного нормального

колебания частоте

0

ω гармонических колебаний отдельного, не

связанного маятника;

• о независимости частоты

1

ω от расстояния

r

;

• об увеличении частоты

2

ω противофазного нормального колебания с

увеличением расстояния

r

:

0

2

12

/ ωωω Jkr+≈ ;

• о равенстве частоты биений

Б

ω разности частот нормальных

колебаний:

12

ωωω −=

Б

;

• об увеличении частоты биений

Б

ω с увеличением расстояния

r

:

0

2

/ ωω Jkr

Б

≈ .

Контрольные вопросы

1. Какова цель работы?

2. Какие формулы являются рабочими?

3. Что Вы будете измерять непосредственно?

4. Что Вы будете определять косвенно?

5. Каким образом Вы будете измерять частоты нормальных колебаний и

частоту биений?

6. Какие графические зависимости Вы ожидаете получить? Что Вы решили

отложить по осям координат?

7. Как Вы собираетесь вычислять погрешности всех величин?

11

8. Вывели ли Вы соответствующие формулы для расчета соответствующих

погрешностей?

9. Как определяется число степеней свободы?

10. Как записывается основное уравнение динамики вращательного

движения?

11. Как выведены уравнения (4) и (5)?

12. Когда уравнения (7), (8) переходят в уравнения гармонических

колебаний?

13. Какие колебания называются нормальными?

14. Что такое явление биений?

15. Когда возникает это явление?

16. Почему биения не представляют собой гармонические колебания?

17. Что такое амплитуда биений? Изобразите график зависимости амплитуды

биений от времени.

18. Почему частота биений равна разности нормальных частот, а не их

полуразности, как это записано в формулах (20), (21) и (27), (28)?

19. Что происходит с энергиями маятников в процессе биений?

20. Подтверждают ли Ваши экспериментальные результаты теоретические

выводы?

Литература

1. Трофимова Т.И. Курс физики: Учеб. пособие для втузов. – М.: Высш. шк.,

1999. – 542 с., § 142, § 144.

1

Лабораторная работа №21

СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ ОДИНАКОВОЙ

ЧАСТОТЫ

Цель работы – научиться измерять разность фаз гармонических

колебаний одинаковой частоты методом сложения колебаний,

экспериментально определить зависимость фазового сдвига между

колебаниями напряжения на двух последовательно соединенных элементах

электрической цепи от частоты и сравнить полученную зависимость с

рассчитанной теоретически.

Теоретическое введение

1. Сложение двух одинаково направленных гармонических колебаний.

При сложении двух одинаково направленных колебаний некоторой

материальной точки результирующее смещение

s

точки равно

алгебраической сумме смещений

1

s и

2

s в каждом из колебаний. Этот же

случай реализуется и при сложении колебаний скалярных физических

характеристик колебательной системы ( давления, силы тока, напряжения и

т.д. ). Если частоты складываемых колебаний равны, то

(

)

111

tcosAs

ϕ

ω

+

=

,

(

)

22

tcosAs

ϕ

ω

+

=

.

Сложение таких колебаний можно произвести, воспользовавшись методом

векторных диаграмм

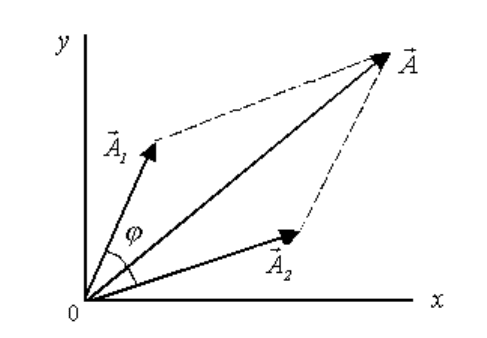
Рис. 1

На рис.1 показано положение векторов

1

A

r

,

2

A

r

и результирующего вектора

A

r

для некоторого момента времени. Угол

ϕ

между векторами

1

A

r

и

2

A

r

равен

12

ϕ

−

. Так как векторы

1

A

r

и

2

A

r

вращаются с одинаковой угловой

скоростью

ω

, угол

ϕ

со временем не изменяется. Следовательно, и

2

результирующий вектор

A

r

вращается с той же угловой скоростью

ω

, а

соответствующие

колебания совершаются с циклической частотой

ω

. Амплитуду

результирующего колебания можно найти по теореме косинусов, согласно

которой

ϕcosAA2AAA

21

2

1

2

++= (1)

Формула (1) позволяет найти амплитуду результирующего колебания

A

,

если известны амплитуды

1

A и

2

A складываемых колебаний и

соответствующая разность фаз

ϕ

. Эту формулу можно преобразовать к виду

21

2

1

2

AA2

AAA

arccos

−−

=ϕ (2)

По формуле (2) можно найти разность фаз

ϕ

, если известны амплитуды

1

A ,

2

A и

A

.

2. Сложение двух взаимно перпендикулярных гармонических колебаний.

Если материальная точка может совершать колебания как вдоль оси

x

,

так и вдоль перпендикулярной к ней оси

y

с одинаковой частотой

ω

, то при

одновременном колебании вдоль этих осей колебания описываются

уравнениями

t

cos

a

x

ω

=

(

)

ϕ

ω

+

=

tcosby , (3)

где

a

и

b

- амплитуды колебаний ,

ϕ

- разность фаз (фазовый сдвиг)

колебаний. Если из этих уравнений исключить время, то после некоторых

преобразований можно получить уравнение траектории движения точки,

которое имеет вид:

ϕϕ

2

sincos

ab

xy

2

b

y

a

x

=−+ (4)

Это уравнение эллипса . Материальная точка описывает этот эллипс за

время, равное периоду складываемых колебаний. Ориентация эллипса и его

размеры зависят от амплитуд

a

и b складываемых колебаний и разности фаз

ϕ

.

Уравнение (3) справедливо не только для колебаний материальной

точки. Так например, подавая переменное электрическое напряжение

1

U на

вход

Y

и напряжение

2

U той же частоты на вход

X

осциллографа , можно

заставить световое пятно на экране осциллографа совершать колебания как

вдоль оси

X

, так и вдоль оси

Y

. На экране осциллографа будет

высвечиваться траектория движения этого пятна – эллипс. На рис.2 показан

вид эллипса для некоторого частного случая.

Из уравнения (4) следует, что при

0x =

3

ϕ

2

sin

b

y

=

или

b

y

sin ±=ϕ .

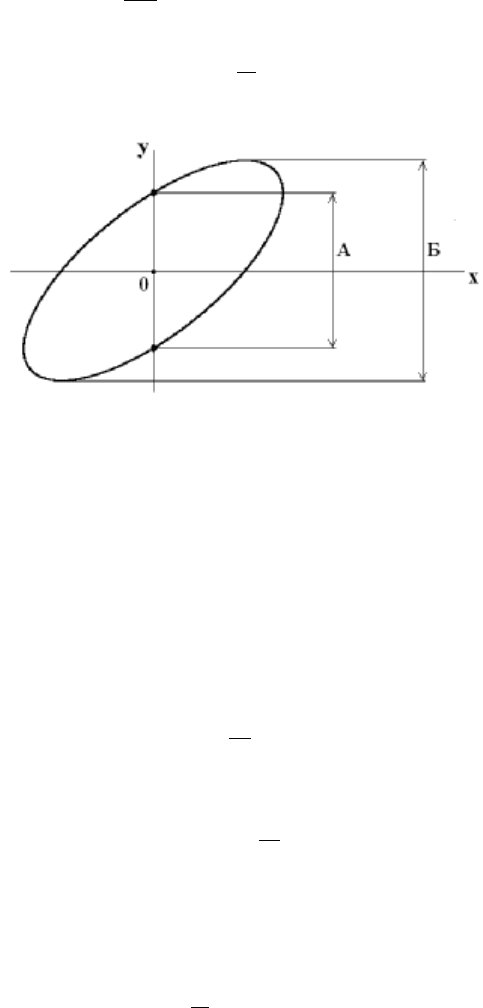
Рис.2

Следовательно, по виду эллипса можно определить

ϕ

sin

и фазовый сдвиг

ϕ

.

Следует отметить, что определить знак

ϕ

sin

, а следовательно и знак

фазового сдвига, по виду эллипса обычно бывает невозможно, поскольку при

большой частоте колебаний невозможно проследить, движется ли световое

пятно вдоль эллипса по часовой стрелке или против. Поэтому в работе будем

определять

ϕ

sin

и фазовый сдвиг только по модулю. В соответствии с

обозначениями, принятыми на рис.2

Б

А

sin =ϕ ,

Б

A

arcsin=ϕ (5)

Поскольку складываемые колебания подаются на разные входы

осциллографа, коэффициенты усиления в каналах которых могут быть

разными, отношение амплитуд

b

a

колебаний светового пятна может не

совпадать с отношением амплитуд напряжений, подаваемых на входы

осциллографа. Однако при измерении фазового сдвига по формуле (5) надо

знать амплитуду колебаний светового пятна только вдоль оси

y

. Амплитуда

колебаний вдоль оси

x

может быть любой.

Анализ ошибки измерения фазового сдвига этим методом показывает,

что наиболее предпочтительным является случай, когда

ba ≈

. Этого можно

достичь, регулируя коэффициенты усиления соответствующих усилителей.

4

Описание экспериментальной установки

Схема установки, предназначенной для изучения сложения колебаний

напряжения в цепи, состоящей из двух последовательно соединенных

элементов с импедансами

1

Z и

2

Z , показана на рис.3.

Рис. 3

Генератор электрических колебаний Г , элементы исследуемой цепи

1

Z и

2

Z ,

а также вольтметр В и входы x и y осциллографа О соединены через

коммутатор К. Коммутатор позволяет осуществить четыре варианта

измерений:

1) измерение напряжения

1

U на элементе

1

Z ;

2) измерение напряжения

2

U на элементе

2

Z ;

3) измерение напряжения

U

на цепочке последовательно соединенных

элементов

1

Z и

2

Z ;

4) измерение разности фаз колебаний напряжения на элементах

1

Z и

2

Z ;

В качестве элемента цепи

1

Z используется резистор

1

R . В качестве элемента

цепи

2

Z используются соединенные параллельно резистор

R

и конденсатор

C

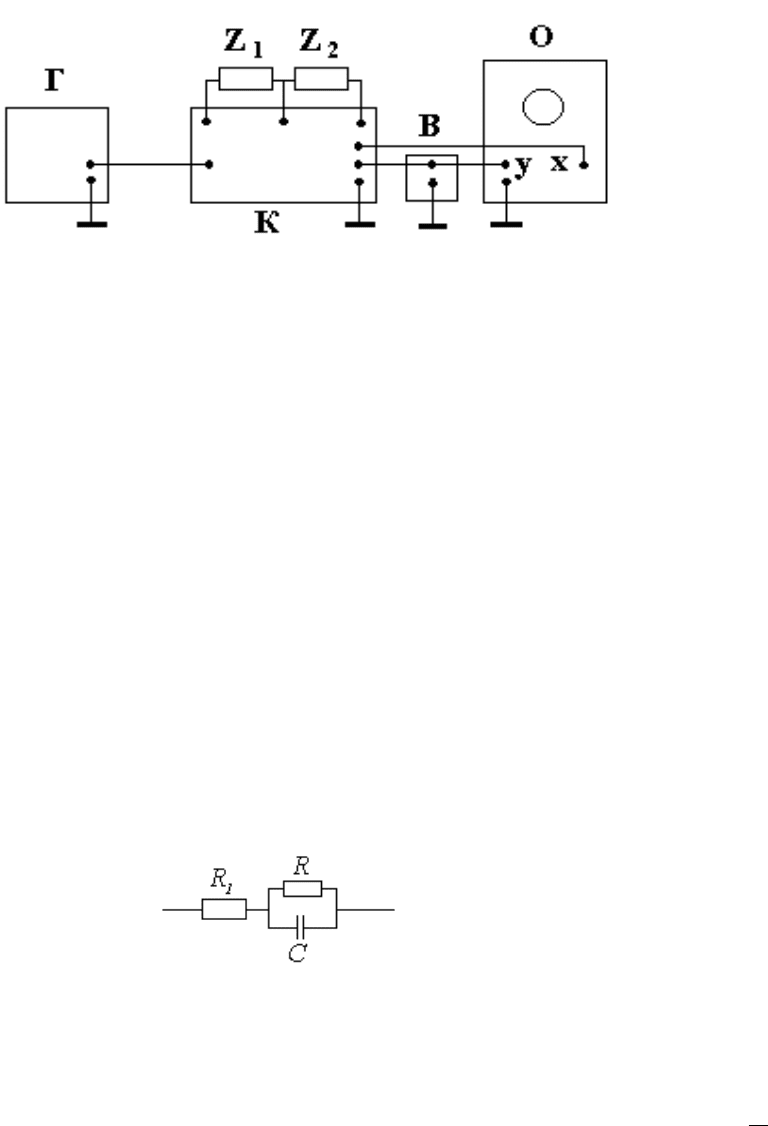
. Соответствующая схема показана на рисунке 4.

Рис.4

Напряжение на резисторе

R

равно напряжению на конденсаторе. Ток через

конденсатор

C

I опережает по фазе ток через резистор

R

I на

2

π

.

Соответст

вующая векторная диаграмма для токов показана на рис.5.

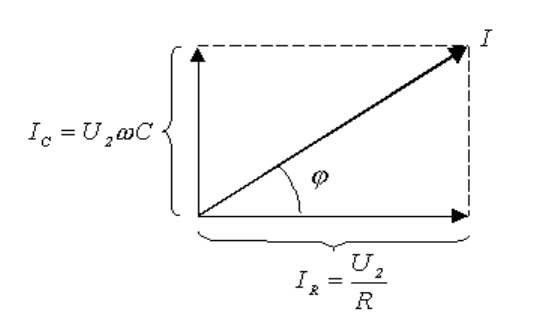
5

Рис. 5

Из приведенной диаграммы следует, что

RC

tg

ω

ϕ

=

(6 )

Так как элементы

1

Z и

2

Z соединены последовательно, через них протекает

один и тот же ток

I

. Напряжение

1

U на резисторе

1

R совпадает по фазе с

этим током. Напряжение

2

U на резисторе

R

совпадает по фазе с током

R

I .

Следовательно , разность фаз между напряжениями

1

U и

2

U такая же , как и

между токами

I

и

R

I , т.е. равна углу

ϕ

, определяемому выражением (6).

Напряжения

1

U ,

2

U и

U

можно измерить как с помощью осциллографа,

так и с помощью вольтметра. Измерения с помощью вольтметра

предпочтительнее, так как точность таких измерений выше. При проведении

этих измерений рекомендуется с помощью осциллографа следить за формой

сигнала, подаваемого с генератора . Она должна быть синусоидальной. В

случае искажения формы сигнала следует уменьшить напряжение на выходе

генератора до уровня, обеспечивающего синусоидальную форму

Задание к работе

1.Измерить с помощью вольтметра напряжения

1

U ,

2

U и

U

в диапазоне

частот, указанном в паспорте установки ( по 10 значений для каждого из

напряжений ).

2. По результатам измерений найти фазовый сдвиг

ϕ

и

ϕ

tg

.

3. Определить фазовый сдвиг

ϕ

и

ϕ

tg

методом фигур Лиссажу для тех же

частот, что и в п. 1.

4. Построить график зависимости

ϕ

tg

от

ω

, рассчитаный теоретически по

формуле (5).

5. На график нанести точки, полученные по п.п. 2 и 3 ( изображение точек,

полученных по п.п. 2 и 3, между собой должны различаться).

6. Экспериментально полученную зависимость

ϕ

tg

от

ω

сравнить с

теоретической. Сделать выводы о степени соответствия результатов,

полученных разными методам

Контрольные вопросы

1. Получите выражение (1) для результирующего колебания.

6

2. Докажите, что при взаимно перпендикулярных колебаниях с

одинаковой частотой траекторией движения точки является эллипс.

3. Как по виду эллипса на экране осциллографа определить разность фаз

колебаний?

4. Получите выражение для ожидаемой зависимости

ϕ

tg

от

ω

.

5. Какой график вы будете строить?

Литература

1. Трофимова Т.И. Курс физики.- М: Высшая школа, 1997.- § 145.

2. Савельев И.В. Курс общей физики.- Кн. 1.- М: Наука. Физматлит, 1998.-

§ 8.8.

3. Детлаф А.А. Яворский Б.М. Курс физики.-М: Высшая школа, 1999.-

§27.4.

Лабораторные работы по курсу общей физики (2-я Редакция 2012 г.)

Подождите немного. Документ загружается.