Лабораторные работы по курсу общей физики (2-я Редакция 2012 г.)
Подождите немного. Документ загружается.


7
4. Построить график зависимости рассчитанных теоретически и
определенных экспериментально периодов колебаний от емкости на
одних и тех же осях. В каких осях строить график решить самостоятельно.
5. При одном из значений емкости
i
C (по указанию преподавателя)
измерить логарифмический декремент
λ
для пяти различных
сопротивлений
k
R . Оценить стандартное отклонение
λ
σ
.Построить график
зависимости
λ
от R (полного сопротивления контура).
6. Вычислить логарифмический декремент для контура по формуле (12) при
тех же значениях сопротивления R, что и в п.5.
7. Полученные в п.6 значения нанести на график, простроенный в
соответствии с п.5.
8. Вычислить критическое сопротивление для контура при одном из
значений емкости конденсатора. Убедиться экспериментально, что при
таком значении сопротивления колебания прекращаются.
9. Сделать вывод о степени соответствия модели колебательного контура с
идеальными элементами R, L и C нашему реальному контуру.
Контрольные вопросы
1. Какие колебания называются свободными? Получите дифференциальное
уравнение, описывающее затухающие колебания в колебательном
контуре.
2. Как выглядит решение дифференциального уравнения для случая
затухающих колебаний? Чему равны период колебаний Т и коэффициент
затухания
β
? Как эти величины выражаются через параметры контура L,
C и R ?
3. Что такое логарифмический декремент? Как он выражается через
параметры контура? Соотношение между
λ
и
β
.
4. Что такое критическое сопротивление? Его выражение через параметры
контура.
5. Как с помощью осциллографа измерить период колебаний T ? В каком
случае период колебаний можно считать равным LCπ2 ?
6. Как с помощью осциллографа измерить логарифмический декремент?
7. Каким требованиям должны удовлетворять катушка индуктивности и
конденсатор, чтобы соответствующий контур наиболее точно описывался
дифференциальным уравнением (3) ?
Литература
1. Савельев И. В. Курс общей физики.- Кн2.- М.: Наука. Физматлит, 1998.-
§ 13.3
2. Трофимова Т. И. Курс физики.- М.: Высшая школа , 1997.-§ 143, 146.
3. Б.М Детлаф А.А.,Яворский. Курс физики.- М.: Высшая школа, 1999.-§
28.1
1
Лабораторная работа № 23 а
Вынужденные колебания в колебательном контуре
Цель работы: Экспериментально исследовать зависимость напряжения на
конденсаторе в электромагнитном колебательном контуре от частоты
последовательно включенной переменной Э.Д.С. Определить резонансную
частоту, сравнить ее с расчетной.
Теоретическое введение
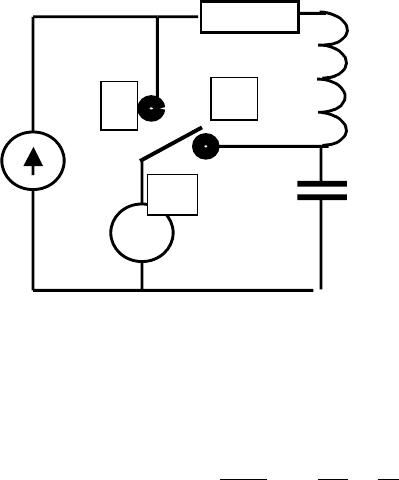
Рассмотрим схему из последовательно соединенных конденсатора,
катушки индуктивности, резистора и генератора переменной ЭДС (рис.1).
Согласно закону Кирхгофа, сумма падений
напряжения на резисторе U
R
= IR и конден-
саторе U
C
= q/C равна сумме действующих в
цепи ЭДС, то есть переменной ЭДС генератора
E
L
= - L dI/dt:
U
R
+ U
C
= Е
L
+ E
Г
(1)
Рис.1
Выражая U
R
, U
C
и Е
L
через заряд конденсатора q и параметры контура L, C и
R (полное сопротивление контура), получаем дифференциальное уравнение
=++
C
q
dt
dq
R
dt
qd
L
2
2
E
m
cos(ωt+φ), (2)
описывающее вынужденные колебания.
Из теории дифференциальных уравнений известно, что при t » β
-1
, где β =
R/2L, решение уравнения (2) представляет собой колебания с частотой ω:
q(t) = cos ωt ; (3)
q
m
можно найти из следующих соображений. В левой части уравнения (2)
стоит сумма трех колебаний. Результат сложения можно найти, используя
метод векторных диаграмм [1]. Для этого запишем явный вид каждого из
этих трех колебаний:
q/C = (q
m
/C)cos ωt
R(dq/dt) = - Rq
m
ω sin ωt = Rq
m
ω cos(ωt+π/2)
L(d
2
q/dt
2
) = - ω
2
Lq
m
cos ωt = ω
2
Lq
m
cos(ωt+π)
V
1
2
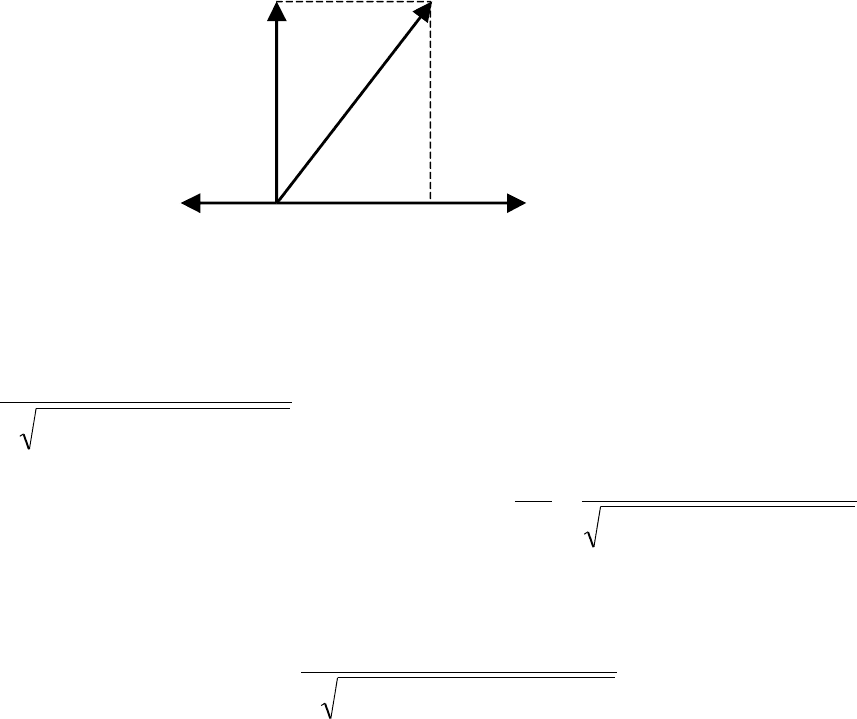
2
и сопоставим каждому колебанию вектор с длиной равной амплитуде
соответствующего колебания. Начальные фазы колебаний определяют
ориентацию векторов относительно горизонтальной оси (см.рис.2).
Rq
m
ω E
m
ω
2
Lq
m
q
m
/C
Рис. 2
Из рисунка очевидно, что ((q
m
/C) - ω
2
Lq
m
)
2
+ (Rq
m
ω)
2
= (E
m
)
2
. Отсюда
находим
2222
0
2
4)(
ωβωω +−
=
L
E
q
m
m
, где β = R/2L ,
2
0
ω
= 1/LC. Амплитуда
напряжения на конденсаторе
2222
0
2
2
0
4)( ωβωω
ω
+−
==
mm
Cm
E
C
q
U .
Выражение для U
Cm
, учитывая связь ω = 2πν, удобно переписать как
функцию частоты ν, измеряемой в герцах:
22222
0
2
2
0
/)( πνβνν
ν
+−
=
L
E
U
m
Cm
(4)
Из формулы (4) видно, что амплитуда напряжения U
Cm
на конденсаторе
зависит от соотношения частот: частоты собственных колебаний ν
0
и частоты
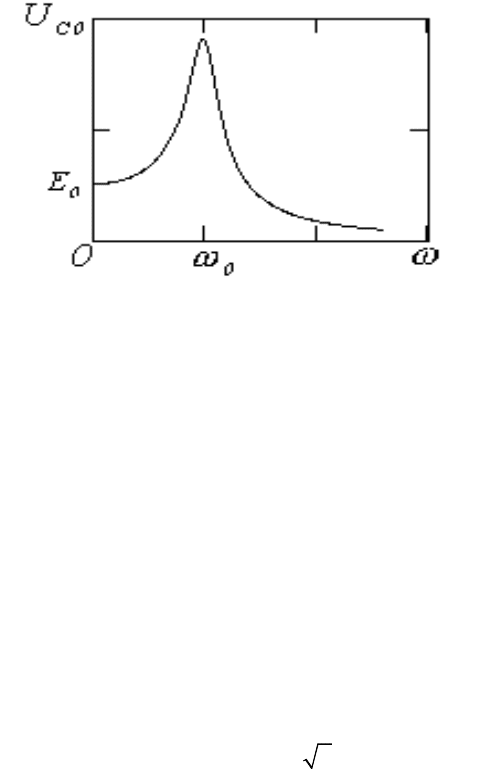
колебаний вынуждающей ЭДС ν. График функции U
Cm
(ν) при нескольких
значениях сопротивления R показан на рисунке 3. Максимальное значение
U
Cm
(ν) достигается при некоторой частоте ν
Р
, называемой резонансной.
Найти ν
Р
можно, исследуя выражение (4) амплитуды вынужденных
колебаний на максимум (можно исследовать на минимум подкоренное
выражение, стоящее в знаменателе). Найдя резонансную частоту ν
Р
,
нетрудно убедиться, что в общем случае она не равна собственной частоте ν
0
,
а тем меньше ее, чем больше коэффициент затухания.
3
Рис.3.
Описание установки
В лабораторной установке (смотри схему на рис.1) напряжение на
конденсаторе измеряется вольтметром в положении 2 переключателя; в
положении 1 вольтметр подключается непосредственно к генератору,
являющемся источником переменной ЭДС регулируемой частоты.
Вольтметр, обладающий большим внутренним сопротивлением, позволяет
измерять переменные напряжения в широком интервале частот. Чтобы
исключить влияние внутреннего сопротивления генератора R
г
на
измеряемые величины напряжений, необходимо выполнение соотношения R
г
< R. В этом случае, в положении 1 переключателя показания вольтметра
практически соответствуют величине E
m
/
2
.
Задание к работе
1) Ознакомиться в лаборатории с инструкцией по пользованию приборами
установки.
2) Рассчитать ν
Р
и ее погрешность по исходным данным установки.
3) При заданных значениях R, изменяя частоту выходного напряжения ге-
нератора и поддерживая постоянное значение амплитуды его напряжения (по
указанию преподавателя), снять частотные характеристики напряжения на
конденсаторе. Особо тщательно проводить измерения вблизи резонансных
частот (для этого, используя расчеты п.2, вначале, определить
экспериментально эти частоты грубо).
4) В общих осях построить графики зависимости U
Cm
от частоты для
различных R. Определить по графикам U
Cm
(ν) резонансные частоты.
Сравнить их с расчетными с учетом погрешностей.
5) По графикам U
Cm
(ν), пользуясь формулой (U
Cm
)
max
= QE
m
, найти
добротность Q контуров при использованных значениях R.
6) Сделать выводы относительно: изменения ν
Р
и Q в зависимости от
сопротивления, включенного в контур; высоты максимумов кривых при
4
разных сопротивлениях; а также совпадения между между резонансными
частотами, найденными экспериментально и вычисленными.
Контрольные вопросы
1) Какие колебания называются вынужденными?
2) Что такое резонанс напряжений на конденсаторе в контуре?
3) Нарисуйте принципиальную схему установки. Для чего необходимо
регулярно проверять удерживается ли первоначально заданное выходное
напряжение генератора?
4) Напишите дифференциальное уравнение вынужденных колебаний.
Запишите и проанализируйте частное решение этого уравнеия.
5) Получите выражение для амплитуды колебаний напряжения на
конденсаторе (выражение (4)).
6) Найдите резонансную частоту для U
Cm
.
7) Получите выражение для амплитуды колебаний тока в цепи и найдите
резонансную частоту для I
Cm
.
8) Как вычислить ω
0
и ν
0
?
9) Какой график вы будете строить в работе? Какой он будет иметь вид?
Проходит ли он через начало координат? Как сдвигается резонансная частота
при увеличении сопротивления контура?
10) Что такое добротность Q колебательного контура? Покажите, что Q
связана с U
Cm
формулой (U
Cm
)
max
≈ QE
m
, справедливой при больших
значениях Q.
11) Получили ли вы то, что ожидали?
12) Приведите примеры применения резонанса в технике.
Литература
1. Савельев И.В. Курс общей физики.- М.:Наука, 1998

1
Лабораторная работа №23 б
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Цель работы – экспериментальное исследование частотной зависимости
напряжения на конденсаторе при вынужденных колебаниях в колебательном
контуре. Определение резонансной частоты, полосы пропускания и
добротности колебательного контура. Сравнение полученных результатов с
рассчитанными теоретически.
Теоретическое введение
Рассмотрим колебательный контур, схема которого показана на рис. 1.
Рис. 1
Будем считать, что контур состоит из идеальных элементов R, L и C .
Последовательно с этими элементами включен генератор гармонических
электрических колебаний с э.д.с.
.cos
0
tEE
ω
=
(1)
Внутреннее сопротивление генератора будем считать настолько малым по
сравнению с сопротивлением резистора R , что им можно пренебречь.
Энергия электромагнитного поля в контуре
C
2
q
2
qL
W
22
ЭМ
+=
&
(2)
Если E = 0, то колебания в контуре являются свободными и энергия
электромагнитного поля убывает, причем
Rq
dt
dW
2ЭМ
&
−= (3)
Электромагнитная энергия переходит в джоулево тепло. При включенном
генераторе, когда
0
E
≠
, энергия от генератора передается контуру и идет на
увеличение
ЭМ
W . В этом случае
EqRq
dt
dW
2
ЭМ
&&
+−= , (4)
где
Eq
&
- электрическая мощность, подводимая к контуру. Колебания в
этом случае уже не являются свободными и называются вынужденными.
2
Из выражения (4) с учетом (1) и (2) можно получить дифференциальное
уравнение
.cos
0
tE
C
q
qRqL ω=++
&&&
(5)
В этом уравнении
qL
&&
- напряжение на катушке индуктивности,
qR
&
-
напряжение на резисторе,
C
q
- напряжение на конденсаторе. Уравнение (5)
выражает второе правило Кирхгофа для последовательного колебательного
контура.
После включения генератора в колебательном контуре сначала
возникает так называемый переходной режим вынужденных колебаний. В
этом режиме в колебательном контуре одновременно совершаются
колебания двух типов. Первый тип – это свободные затухающие колебания,
совершающиеся с частотой
22
0
βωω −=
′
. Второй тип – незатухающие вынужденные колебания с
частотой вынуждающей силы (с частотой
ω
генератора). При работе в этом
режиме RqEq
2
&
&
> . Происходит процесс накопления энергии
ЭМ
W в
контуре. Через промежуток времени
β
∆
/
5
t
≈
, где
β
- коэффициент
затухания , колебания первого типа практически исчезнут и контур будет
работать в режиме установившихся вынужденных колебаний. В этом
режиме мощность потерь энергии в контуре полностью компенсируется
подводимой электрической мощностью. Энергия электромагнитного поля и
амплитуда колебаний в контуре со временем не изменяются. В настоящей
работе будут рассматриваться колебания именно в этом, установившемся
режиме. Решение уравнения (5) в этом случае должно иметь вид:
(
)
00
tcosqq
ϕ
ω
+
=
, (6)
то есть должны существовать такие значения
0
q и
0
ϕ
, при которых
подстановка выражения (6) в дифференциальное уравнение обращает это
уравнение в тождество.
Определим амплитудное значение заряда
0
q . Для этого подставим
выражение (6) в уравнение (5). Получим
( ) ( )
tcosEtcos
C
q
2
tcosRqtcosLq
00
0
00o
2
0
ωϕω
π
ϕωωπϕωω =++
+++++
(7)
или
( ) ( )
tcosEtcosU
2
tcosUtcosU
0o0C00R00L
ωϕω
π
ϕωπϕω =++
+++++ ,
(8)
где
3
2
00L
LqU ω=
ω
00R
RqU
=
(9)
C
q
U
0
0C
=
амплитудные значения напряжений на элементах контура. В отличие от
мгновенных значений напряжений на элементах контура и мгновенного
значения э.д.с. генератора, сумма амплитудных значений напряжений не
равна амплитуде э.д.с. генератора.
Для решения задачи сложения колебаний удобно воспользоваться
методом векторных диаграмм. Диаграмма, соответствующая уравнению (8)
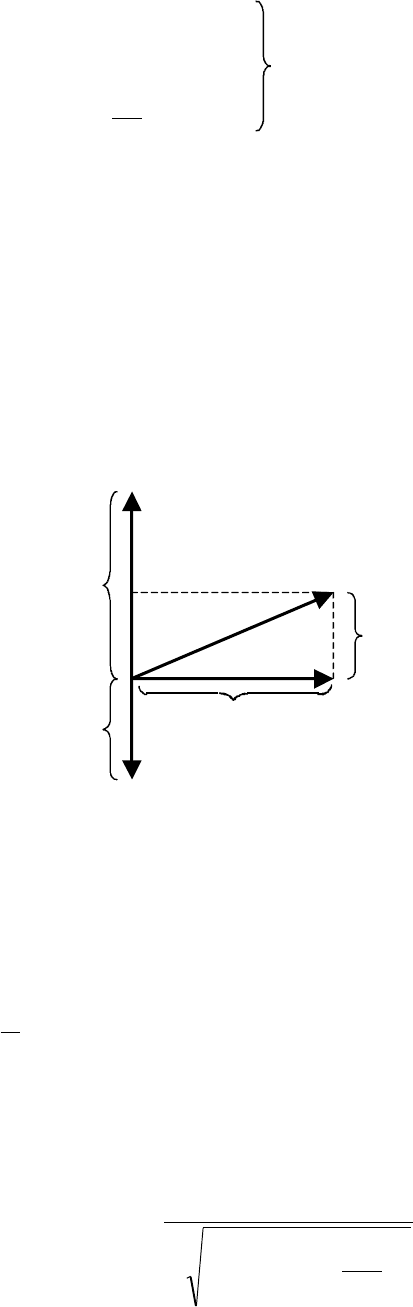
показана на рис. 2.
L
U
E
0L
U
0
E
(
)
0C0L
UU
−
0C
U
R
U
0R
U
C
U
Рис. 2
Направление векторов на диаграмме зависит от времени. Векторы
вращаются против часовой стрелки с угловой скоростью
ω
. Однако
взаимное расположение векторов при этом не изменяется. Диаграмма,
изображенная на рис.2 соответствует моменту времени, когда
1
2
tcos
0
=
++
π
ϕω . Из рис. 2 следует, что
(
)
2
0C0L
2
0R
2
0
UUUE −+= (10)
Если в это уравнение подставить амплитудные значения напряжений из (9) и
решить это уравнение относительно
0
q , то получим выражение
2
2
0
0
C
1
LR
E
q
−+
=
ω
ωω
(11)
Экспериментально для проверки теоретических выводов гораздо проще
измерить не амплитудное значение заряда
0
q , а пропорциональную ему
величину – амплитуду напряжения на конденсаторе. Амплитуда напряжения
на конденсаторе
4
2
2
00
0C
C
1
LRC
E
C
q
U
−+
==
ω
ωω
(12)
Учитывая, что
0
LC
1
ω=
; β=
L2
R
, выражение (12) преобразуем к виду
( )
22
2
2
0
2
2
00
0C
4
E
U
ωβωω
ω
+−
= (13)
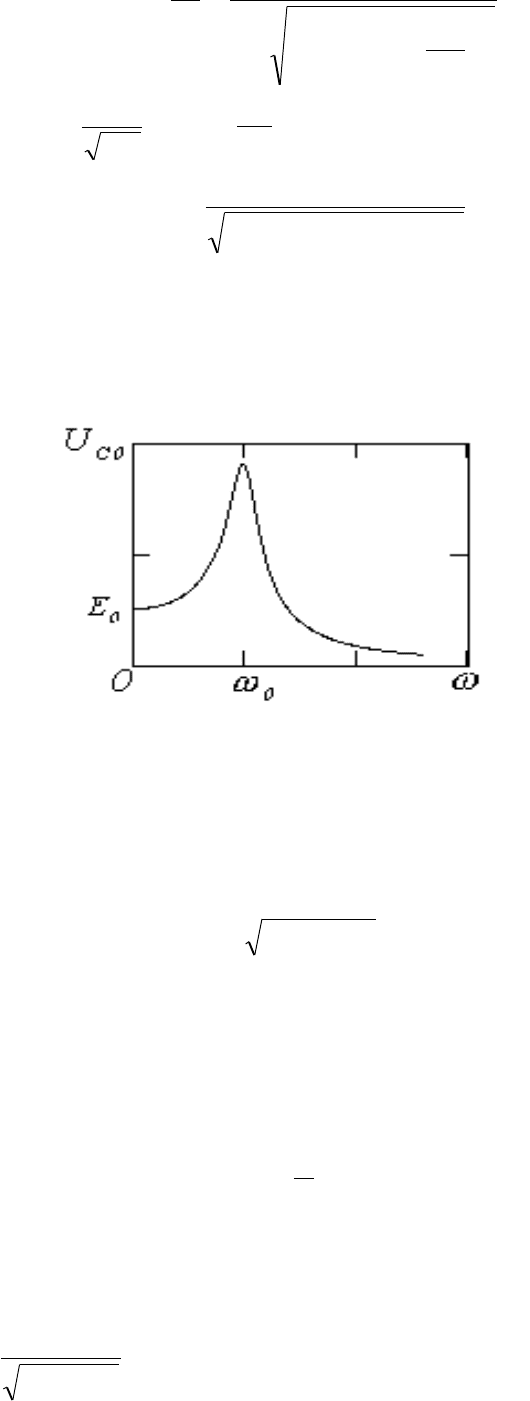
На рис. 3 приведен график зависимости
0C
U от
ω
при постоянном значении
0
E (для частного случая, когда
0
14,0
ω
β
=
).
Рис. 3
Из рисунка следует, что зависимость
0C
U от
ω
проходит через максимум.
Соответствующая кривая называется резонансной кривой. Частота, на
которой резонансная кривая проходит через максимум, называется
резонансной частотой. Исследовав выражение (13) на максимум, получим
выражение для резонансной частоты
22
0Р
2βωω −= (14)
В большинстве используемых на практике контуров
2
0
2
ωβ << и резонансная
частота
Р
ω
практически не отличается от
0
ω
.
Одной из важных характеристик колебательного контура является его
добротность. Добротность
Q
определяется как величина, обратно
пропорциональная логарифмическому декременту
λ
:
λ
π
=Q (15)
Логарифмический декремент
λ
связан с коэффициентом затухания
β
и
периодом свободных колебаний соотношением
T
β
λ =
, (16)
где
22
0
2
T
βω
π
−
= .

5
При
2
0
2
ωβ << для логарифмического декремента получим выражение
0
2
ω
πβ
λ = ,а для добротности –
β
ω
2
Q
o
= (17)
Для колебательного контура
LC
1
0
=ω ;
L
2
R
=β , поэтому добротность
может быть выражена через параметры элементов контура формулой
C
L
R
1
Q = (18)
Самое большое значение амплитуда напряжения на конденсаторе
0C
U имеет на резонансной частоте
Р
ω
(при условии, что
0
E не зависит от
частоты). Определим, чему равно отношение
0
0C
E
U
на частоте
Р
ω
ω =
. В
этом случае из (13) следует
( )
2Р
2
2
2
0
2
Р
2
0
0
0C
4
E
U
ωβωω
ω
+−
= . (19)
При
2
0
2
ωβ << можно считать, что
0Р
ω
ω
=
. Тогда
β
ω
2E
U
0
0
0C
= (20)
откуда в соответствии с формулой (7) имеем
Q
E
U
0
Co
= (21)
Таким образом, для того, чтобы экспериментально определить добротность
контура, достаточно измерить амплитуду напряжения
0C
U и амплитуду э.д.с.
генератора
0
E на частоте резонанса.
Как известно, максимальное значение амплитуда
0C
U имеет на
резонансной частоте. Существует такая частота
Р1
ω
ω
<
, на которой
амплитуда напряжения на конденсаторе равна 21 от максимальной.
Существует частота
Р2
ω
ω
>
, на которой амплитуда напряжения на
конденсаторе также равна 21 от максимальной. Интервал частот от
1
ω
до
2
ω
называется полосой пропускания контура. В пределах этого интервала
амплитуда напряжения на конденсаторе больше (или равна) 21 от
