Kutz M. Handbook of materials selection

Подождите немного. Документ загружается.

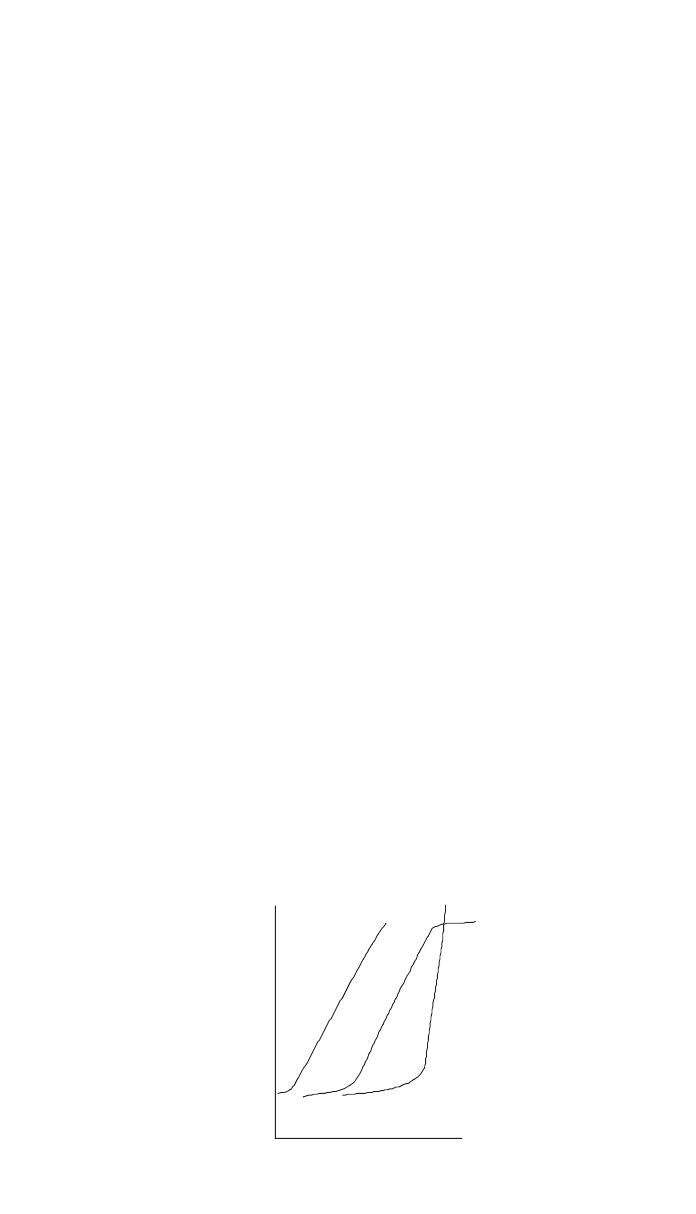
668 NONDESTRUCTIVE INSPECTION

Log (relative exposure)

Density Log(B /B)

321

Type K

Type F

Type M

Fig. 17 Density or darkness of X-ray ﬁlm versus relative exposure for three common ﬁlms.

ment by its weight fraction in the material and summing these quantities. Mul-

tiplying this quantity by the density of the material yields its attenuation

coefﬁcient. This procedure is not often used in practice because the results are

valid only for a narrow band of wavelengths. In practice, radiographic equiva-

lency factors are used instead. This process points out that each element in a

material contributes to the attenuation coefﬁcient by an amount proportional to

its atomic percentage in the composition.

4.4 Film-Based Radiography

The classical method of recording an X-ray image is with ﬁlm. Because of the

continued importance of this medium of recording and the fact that much of the

technology associated with it is applicable to newer solid-state recording meth-

ods, this next section explores ﬁlm radiography in some detail.

The relationship between the darkness produced on an X-ray ﬁlm and the

quantity of radiation falling on it is shown in Fig. 17. This is a log-log plot of

darkness or ﬁlm density and relative exposure. Varying the time of exposure,

intensity of the beam, or specimen thickness will change the ﬁlm density. The

slope of the curve along its linear portion is referred to as the ﬁlm gamma,

␥

Film has characteristics that are quite analogous to electronic devices. For ex-

ample, the greater the gamma or ampliﬁcation capability of the ﬁlm, the smaller

its dynamic range—the range of exposures over which density is linearly related

to thickness. If it is necessary to use a high gamma ﬁlm to detect very subtle

ﬂaws in a part with a wide range of thickness, then it will be necessary to expose

several different ﬁlm types in the same cassette—see Fig. 18. In this way, each

ﬁlm will be optimized for ﬂaw detection in a narrow range of thickness of the

part.

Using what we have learned so far, it is possible to calculate the minimum

detectable ﬂaw size for a speciﬁc RT situation. A method is even available to

check the radiographic procedure to determine if it has achieved the calculated

capability. This procedure does not ensure that the radiograph was taken with

the specimen in the proper orientation; it only provides a method of checking

the radiographic procedures for proper execution. This is covered in the section

on penetrameters (Section 4.5).

4 RADIOGRAPHY 669

Log (relative exposure)

Density, Log(B /B)

123

12345

Fig. 18 Density versus relative exposure for ﬁlms that could be used in a multiple ﬁlm expo-

sure to obtain optimum ﬂaw delectability in a complex part.

No. #

Fig. 19 Schematic of typical ﬁlm penetrameter.

Using knowledge of the minimum density difference that is detectable by the

average radiographic inspector, the following relationship may be derived that

relates the radiographic sensitivity S to both RT parameters and thickness

changes in the specimen:

2.3

S ⫽

␥

⫻

␮

⫻ x

where S is the radiographic sensitivity in percent,

␥

is the ﬁlm gamma for the

exposure conditions used,

␮

is the attenuation coefﬁcient of the specimen ma-

terial, and x is the maximum thickness of the part associated with the radio-

graphic ﬁlm. To check the RT process to determine if this sensitivity was

achieved the radiographer uses a penetrameter.

4.5 The Penetrameter

An example of a penetrameter is shown schematically in Fig. 19, while its image

on a radiograph is shown schematically in Fig. 20. This type of penetrameter

was chosen because it is easily related to the previous discussion of radiographic

sensitivity. This penetrameter is quite simply a thin strip of metal or polymeric

material in which three holes of varying sizes are machined or punched. It is

composed of the same material as the specimen and has a thickness of 1, 2, or

4% of its maximum thickness. The holes in the penetrameter have diameters

that are 1, 2, and 4 times its thickness. The sensitivity achieved for each radi-

ographic is determined by noting the smallest hole just visible in the thinnest

670 NONDESTRUCTIVE INSPECTION

Fig. 20 Radiograph of the penetrameter shown in Fig. 19. The 1T hole is just visible indicating

the resolution obtained in the radiograph.

Table 3 Sensitivity versus the Smallest

Hole Just Visible in the Thinnest

Penetrameter

Sensitivity, S (%)

Quality Level

(%T–Hole Diameter)

0.7 1–1T

1.0 1–2T

1.4 2–1T

2.0 2–2T

2.8 2–4T

4.0 4–2T

penetrameter on a ﬁlm and by using Table 3. By calculating the radiographic

sensitivity and then noting the level achieved in practice, the radiographic pro-

cess can be quantitatively evaluated. While this procedure does not offer any

guarantee of ﬂaw detection, it is quite useful in evaluating the effectiveness the

RT process.

Almost all variables of the radiographic process may be easily and rapidly

changed with the aid of tables, graphs, and nomograms, which are usually pro-

vided by ﬁlm manufacturers free of charge. For more information in this regard

the reader is referred to the commercial literature.

4.6 Real-Time Radiography

While ﬁlm radiography represents the bulk of the radiographic NDE performed

at this time, new methods of both recording the data and analyzing it are coming

into widespread usage. For example, ﬁlmless radiography (FR) or real-time (RT)

radiography testing uses solid-state detectors or television detection and image-

processing methods instead of ﬁlm to record the image. These methods have

several advantages along with some disadvantages. For example, FR permits

viewing a radiographic image while the specimen is being moved. This often

permits the detection of ﬂaws that would normally be missed in conventional

ﬁlm radiography because of the limited number of views or exposures usually

taken—remember that the X-ray beam must pass along a cracklike ﬂaw in order

to be detectable. Additionally, the motion of some ﬂaws enhances their detect-

ability because they present the inspector with a different image as a function

of time than he or she is accustomed to viewing. Additionally, image enhance-

4 RADIOGRAPHY 671

Fig. 21 Computed tomography of ﬂashlight.

ment techniques can now be economically applied to these images because of

the availability of inexpensive, fast computing hardware. The price to be paid

for these advantages is the lower resolution of the FR image compared to ﬁlm.

Typical resolution capabilities of FR systems are in the range from 4 to perhaps

20 line pairs/mm, while ﬁlm resolution capabilities are in the range from 10 to

100 line pairs/mm. This means some very ﬁne ﬂaws may not be detectable with

FR and the inspector must resort to ﬁlm. However, in cases where resolution is

not the limiting factor in delectability, the beneﬁts of software-enabled image

enhancement can be signiﬁcant. While the images on ﬁlm may also be enhanced

using the image-processing schemes, they cannot be performed in real or near

real time, as can be done with a totally electronic system.

4.7 Computed Tomography

Another advance in industrial radiography with and unrealized capability to link

NDE with engineering design and analysis is computed tomography (CT). The

principle advantage of this method is that it produces an image of a thin slice

of the specimen under examination. This slice is parallel to the path of the X-

ray beam as it passes through the specimen as contrasted to the image produced

by classical radiography, where the image is formed on a plane perpendicular

to the path of the X-ray beam on passage through the specimen. The classical

radiographic image can be difﬁcult to interpret because it collapses all of the

image information in the specimen between the source of X-rays and the re-

cording media, whereas the CT image is computed or calculated from X-ray

intensity data and does not contain information from planes outside the thin

slice.

This comparison is best explained with images with these two modalities.

Figure 13 shows a typical radiograph where one can easily see the image of the

top and bottom surfaces of the tube under inspection. Contrast this with the

image in Fig. 21 that shows a CT slice through a ﬂashlight. The individual

672 NONDESTRUCTIVE INSPECTION

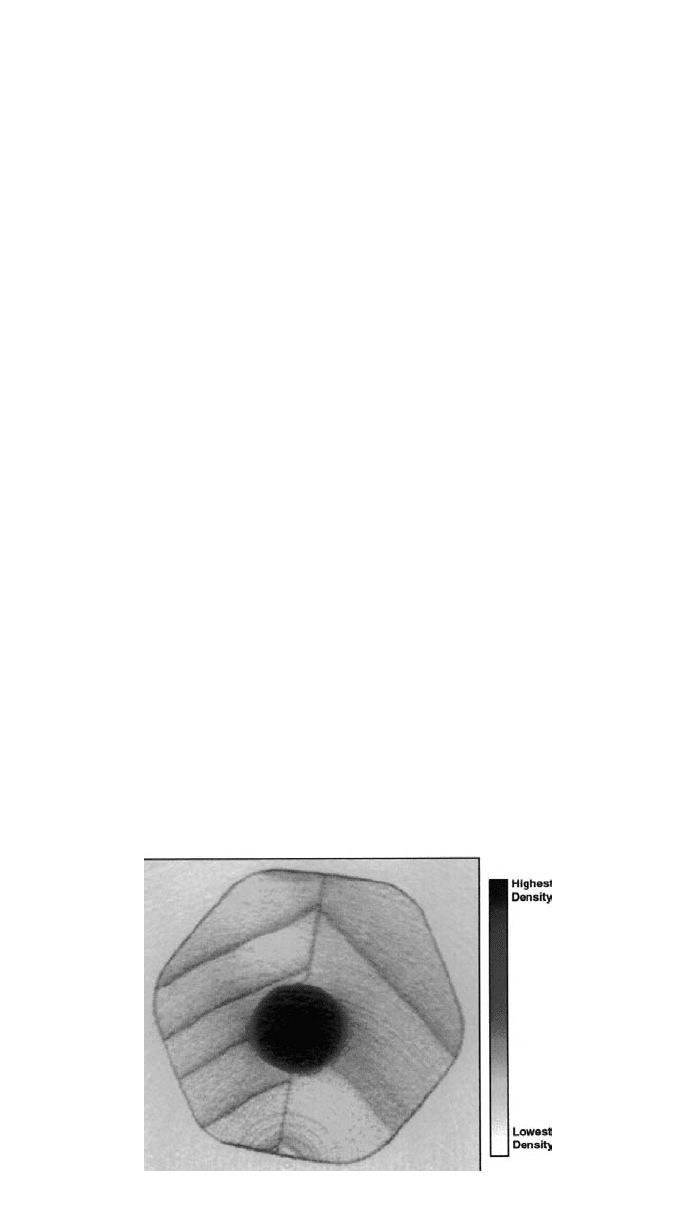
Fig. 22 Computed tomograph of a pencil. The reader will note the yearly growth rings and

even the growth variations within a single growing season.

components of the ﬂashlight are easily visible and any misplacement of its com-

ponents or defects in its assembly could be easily detected. An image on a ﬁner

scale than this can clearly reveal microstructural details of a material as shown

in Fig. 22. Everyone will recognize that this is a pencil. Not only are the key

features clearly visible, but even the growth rings of the wood are clearly visible.

In fact, the details of the growth during each season are visible as rings within

rings. The information in the CT image contrasted with conventional radiographs

is striking. First, the delectability of a defect is independent of its position in

the image. This is not the case with the classical radiograph where the defect

delectability decreases signiﬁcantly with depth in the specimen because the de-

fect represents a smaller change in the attenuation of the X-ray beam as the

depth increases. Second, the defect delectability is very nearly independent of

its orientation. This again is clearly not the case with classical radiography. The

extent to which CT could alter radiography is only now being explored. New

applications are being discovered frequently. For example, with the computed

digital image of CT it is possible to search for various ﬂaw conditions using

computer analysis and relieve the inspector of much of the tedium of examining

structures for the odd ﬂaw. In addition, it is possible to link the digital CT image

with ﬁnite-element analysis software to examine precisely how the ﬂaws present

will affect such parameters as the stress distribution, heat ﬂow, etc. With little

effort one could analyze the full three-dimensional performance of many engi-

neering structures.

5 EDDY CURRENT INSPECTION

Eddy current methods are used principally to inspect electrically conducting

components for near-surface ﬂaws such as cracks and voids, heat treatment con-

dition, external dimensions and wall thickness of thin-walled tubing, and thick-

ness of nonconducting coatings on a metallic substrate.

Quite often several of

these conditions can be monitored simultaneously if instrumentation capable of

multiple frequencies is used and the results are analyzed using computer algo-

rithms.

5 EDDY CURRENT INSPECTION 673

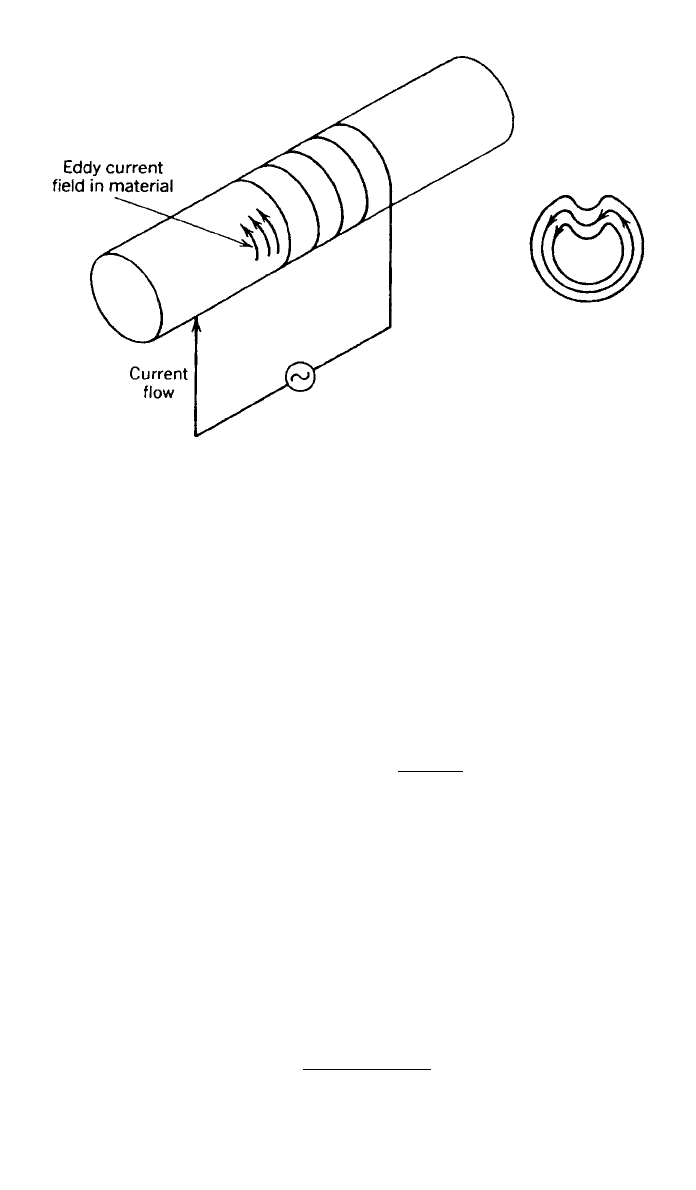
This NDE method is based on the principle that eddy currents are induced in

a conducting material when a coil or array of conductors (probe) with an alter-

nating or pulsating electric current is placed in close proximity to the surface of

the material. The induced currents create an electromagnetic ﬁeld that opposes

the ﬁeld of the inducing coil in accordance with Lenz’s law. The eddy currents

circulate in the part in closed, continuous paths, and their magnitude depends

on several variables. The ﬁrst is the magnitude and frequency of the current in

the inducing coil. Second, is the coil’s shape and position relative to the surface

of the part, the electrical conductivity, magnetic permeability, and shape of the

part. Finally, there are the inﬂuences of any discontinuities or inhomogenities

within the material. Therefore, the eddy currents are useful in exploring these

properties of test materials, as well as any discontinuities or variations in ge-

ometry and dimensions of materials.

5.1 Skin Effect

Since alternating currents are necessary to eddy current inspection, information

from the inspection is limited to the near-surface region by the skin effect. Within

the material, the eddy current density decreases rapidly with distance from the

surface. The density of the eddy current ﬁeld falls off exponentially with depth

and diminishes to a value of about 37% of the at-surface value at a depth referred

to as the standard depth of penetration (SDP). The SDP in meters may be cal-

culated with the simple formula

SDP ⫽

兹

␲

␴␮

where ƒ is the test frequency in hertz,

␴

is the test material’s electrical conduc-

tivity in mho/m (see Appendix B for a table of conductivities for common

metals), and

␮

is its permeability in H/m. This latter quantity is the product of

the relative permeability of the specimen, 1.0 for nonmagnetic materials, and

the permeability of free space, which is 4

␲

⫻ 10 H/m.

⫺

5.2 Impedance Plane

While the SDP is used to give an indication of the depth from which useful

information can be obtained, the choice of the independent variables in most

test situations is usually made using the impedance plane diagram suggested by

Forster.

It is theoretically possible to calculate the optimum inspection param-

eters from numerical codes based on Maxwell’s equations, but this is a tedious

task that is justiﬁed only in special situations.

The eddy currents induced at the surface of a material are time varying and

have amplitude and phase. The complex impedance of the coil used in the in-

spection of a specimen is a function of a number of variables. The effect of

changes in these variables can be conveniently displayed with the impedance

diagram that displays the variations in amplitude and phase of the coil impedance

as functions of the dependent variables specimen conductivity, thickness, and

distance between the coil and specimen or lift-off. For the case of an encircling

coil on a solid cylinder, shown schematically in Fig. 23, the complex impedance

plane is displayed in Fig. 24. The reader will note that the ordinate and abscissa

674 NONDESTRUCTIVE INSPECTION

Fig. 23 Schematic representation for an eddy current inspection of a solid cylinder.

Also shown are the eddy current paths within the cross section of the cylinder

in the vicinity of the crack.

are normalized by the inductive reactance of the empty coil. This eliminates the

effects of the coil/specimen geometry. The numerical values are shown on the

large curve, called reference numbers. These numbers are used to combine

the effects of conductivity and size of the test specimen and the frequency of

the measurement into a single parameter. In this way, the diagram is useful for

most test conditions encountered by the NDE inspector. The reference numbers

shown on the outermost curve are obtained with the following relationship, for

nonmagnetic materials:

Reference # ⫽ r兹2

␲

␮␴

where r is the radius of the bar in meters, ƒ is the frequency of the test in hertz,

␮

is the magnetic permeability of free space (4

␲

⫻ 10 H/m), and

␴

is the

⫺

conductivity of the specimen in mho/m. The outer curve in Fig. 24 is useful

only for the case where the coil is the same size as the solid cylinder, which

almost never happens. For those cases when the coil is larger than the test

specimen, which is usually the case, a coil-ﬁlling factor is calculated. This is

quite easily accomplished with the following formula:

diameter

specimen

N ⫽

冉冊

diameter

coil

Figure 24 shows the impedance plane with a curve for a cylinder/coil inspection

geometry with a ﬁll factor of 0.75. Note that the reference numbers on the

ordinate representing the different ﬁll factors can be determined by projecting a

5 EDDY CURRENT INSPECTION 675

Fig. 24 Normalized impedance diagram for a long encircling coil on a solid, nonferromagnetic

cylinder. For N ⫽ 1 the coil and cylinder have the same diameter, while for N ⫽ 0.75 the coil is

approximately 1.155 times larger than the cylinder.

straight line from point 1.0 on the ordinate to the reference number of interest.

This is shown for reference number 5.0. Both the ﬁll factor and the reference

number change when the size of either the specimen or coil changes. This is

shown in Fig. 24 for solid cylinders. The other geometry of general interest is

the thin-walled tube—remember that the skin effect limits the thickness of a

conductor that may be inspected.

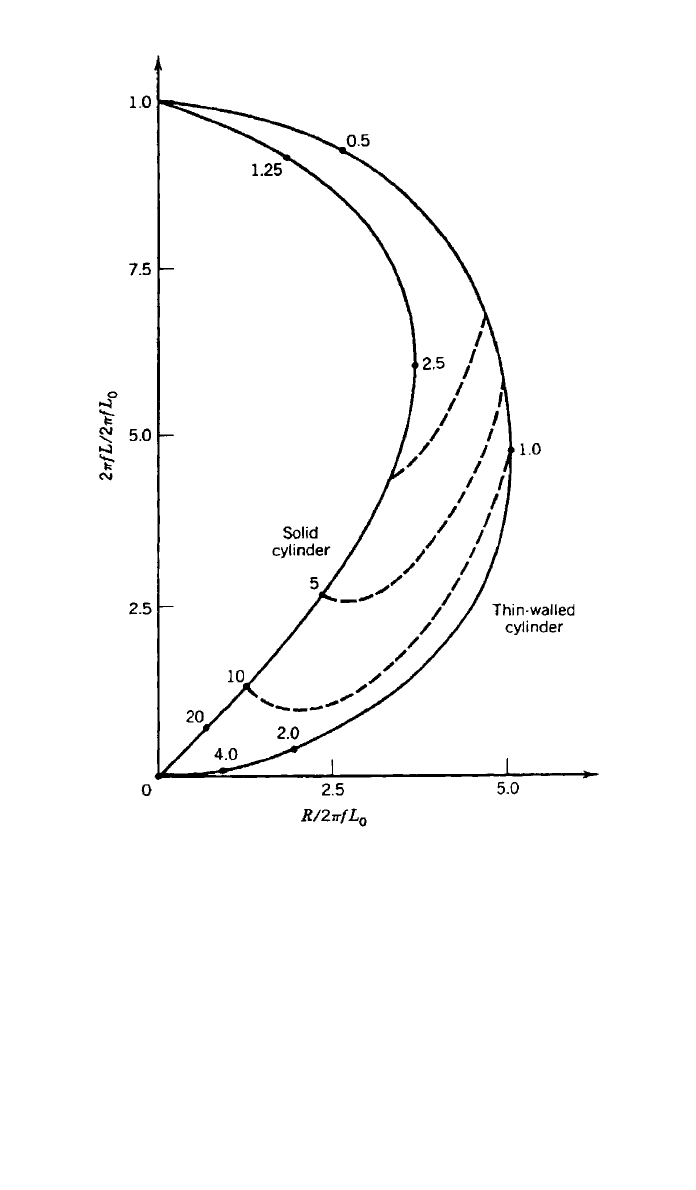
For an inﬁnitely thin-walled tube the impedance plane is shown in Fig. 25.

Also included in this ﬁgure is the curve for a solid cylinder. The curve segments

676 NONDESTRUCTIVE INSPECTION

Fig. 25 Normalized impedance diagram for a long encircling coil on both a solid and

thin-walled conductive but nonferromagnetic cylinders. The dashed lines represent the

effects of varying wall thickness.

that connect these two extreme cases are for walled cylinders of varying thick-

ness. The semicircular curve for the thin cylinder is used in the same manner

as described above.

5.3 Lift-Off of Inspection Coil from Specimen

In many inspection situations the only independent variables are frequency and

lift-off. High frequencies are used for detecting defects such as surface cracks

or corrosion, and low frequencies are mostly used to detect deeply buried de-

fects. While it is possible to change the coil shape and measurement conﬁgu-

ration, the reader is referred to the literature for a discussion of the effects of

these more complex variables. The relationships discussed thus far would seem

5 EDDY CURRENT INSPECTION 677

Fig. 26 Effects of various changes in inspection conditions on local signal changes

in the impedance plane of Fig. 25. Phase differentiation is relatively easily accomplished

with current instrumentation.

of little practical usefulness. However, if a small section of Fig. 25 is expanded

as shown in Fig. 26, then their utility of a well-chosen frequency will become

apparent. In this ﬁgure, vectors represent small changes in thickness, lift-off,

and conductivity. Since these vectors all point in different directions, the signals

that they represent have different phases. Thus, instrumentation with phase dis-

crimination circuitry can differentiate among these different conditions. Changes

in conductivity can arise from several different conditions, the most important

of which is due to material inhomogeneity. For example, aluminum alloys can

have quite different conductivities depending either on their heat treatment or

the presence of cracks or voids. These ﬂaws decrease the apparent conductivity

of the specimen because the eddy currents must either travel a longer distance

to complete their circuit or the material presents a more resistive path. There

are other important eddy current inspection capabilities that cannot be covered

in this brief description of this important tool. These include the inspection of

ferromagnetic alloys, plate and sheet stock, and the measurement of ﬁlm thick-

ness on metallic substrates. For a treatment of these and other special applica-

tions of eddy current NDE, the reader is referred to the Nondestructive Testing

Handbook, Vol. 4, Electromagnetic Testing.

There are many methods of making and displaying eddy current measure-

ments. Two of the more common methods are shown schematically in Fig. 27.

In the absolute coil arrangement very accurate measurements can be made of

the difference between the two different samples. One can be a standard, while

the other is the component in question. In the differential coil arrangement the

differences between two variables at two slightly different locations are com-

pared. For this arrangement slightly varying dimensions and conductivity are not

sensed, while singularities such as cracks or voids are highlighted even in the

presence of other more slowly changing variables. The electronic circuitry used

to accomplish each of these measurements can vary dramatically depending on

the inspection. This aspect of eddy current testing will not be covered here, and

the reader is referred to the manufacturers and engineering literature for details

of the appropriate electronic circuitry.