Kurfess T.R. Robotics and Automation Handbook
Подождите немного. Документ загружается.

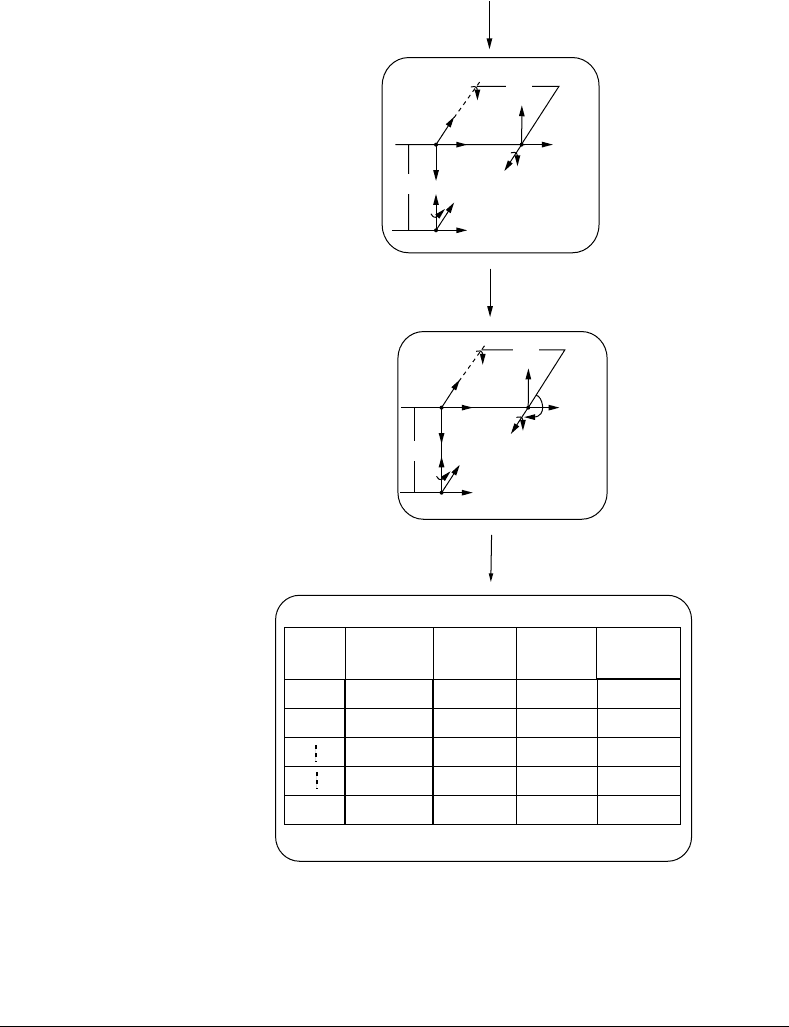
8
-6 Robotics and Automation Handbook
Axis
Number
Twist angle
a
i
Link length
a
i
Link offset
d
i
Joint angle
q
i
1
2
n
a
1
a
2
a
n
a
1
a
2
a
n
d
1
d
2
d
n
q
1
q
2
q
n
D-H Parameters Table
Z
1
q
3
Y
2
Z
2
X
2
Y
1
q
2
Y
0
q
1
X
0
Z
0
X
1
a
2
d
1
a
2
Determine a
i
Z
1
Z
0
q
3
Y
2
Z
2
X
2
Y
1
q
2
Y
0
q
1
X
0
X
1
a
2
d
1
Determine
d
i
and
a
i
FIGURE 8.4 (Continued).
8.3 Algorithm for Determining the Homogenous Transformation
Matrix, A
◦
n
After determining the D-H parameters, the next step is to derive the homogeneous transformation matrix
from one frame to the next. We will denote the U
i
(θ
i
) matrix as the rotation matrix about the Z
i−1
axis while the V
i
(α
i
) matrix as the rotation matrix denoting the rotation about the X
i
axis. To perform
coordinate transformation from reference frame {F
i
} to reference frame {F
i−1
},weneedtoderivethe
rotation matrix and the displacement vector. The rotation matrix from {F
i
} to {F
i−1
} is given by
R
i−1
i
= U
i
V
i
(8.14)
Copyright © 2005 by CRC Press LLC
D-H Convention 8
-7
where U
i
(θ
i
)isgivenby
U
i
(θ
i
) =
cos(θ
i
) −sin(θ
i
)0
sin(θ
i
) cos(θ
i
)0
001
(8.15)
and V
i
(α
i
)isgivenby
V
i
(
α
i
)
=
10 0
0 cos(α
i
) −sin(α
i
)
0 sin(α
i
) cos(α
i
)
(8.16)
The homogeneous transformation matrix transforming coordinates from {F
i
} to {F
i−1
} is given by
A
i−1
i
= A
i−1
i
A
i
i
(8.17)
where A
i
i
is the screw displacement about the axis x
i
through an angle α
i
and distance a
i
. Similarly, A
i−1
i
is the screw displacement about the axis z
i
through an angle θ
i
and distance d
i
. The expression for A
i−1
i
and A
i
i
is given by
A
i−1
i
=
0
U
i
3×3
0
d
i
000
1
(8.18)
A
i
i
=
a
i
V
i
3×3
0
0
000
1
(8.19)
Consequently,
A
i−1
i
=
0
U
i
0
d
i
000
1
a
i
V
i
0
0
000
1
=
U
i
V
i
U
i
s
i
01
(8.20)
Expanding the various terms in Equation (8.20) we get
U
i
V
i
=
cθ
i
−sθ
i
0
sθ
i
cθ
i
0
001
10 0
0 cα
i
−sα
i
0 sα
i
+cα
i
=
cθ
i
−sθ
i
cα
i
sθ
i
sα
i
sθ
i
cθ
i
cα
i
−cθ
i
sα
i
0 sα
i
+cα
i
U
i
s
i
=
cθ
i
−sθ
i
0
sθ
i
cθ
i
0
001
a
i
0
0
+
0
0
d
i
=
cθ
i
a
i
sθ
i
a
i
d
i
(8.21)
where
s
i
=
a
i
0
d
i
(8.22)
Copyright © 2005 by CRC Press LLC
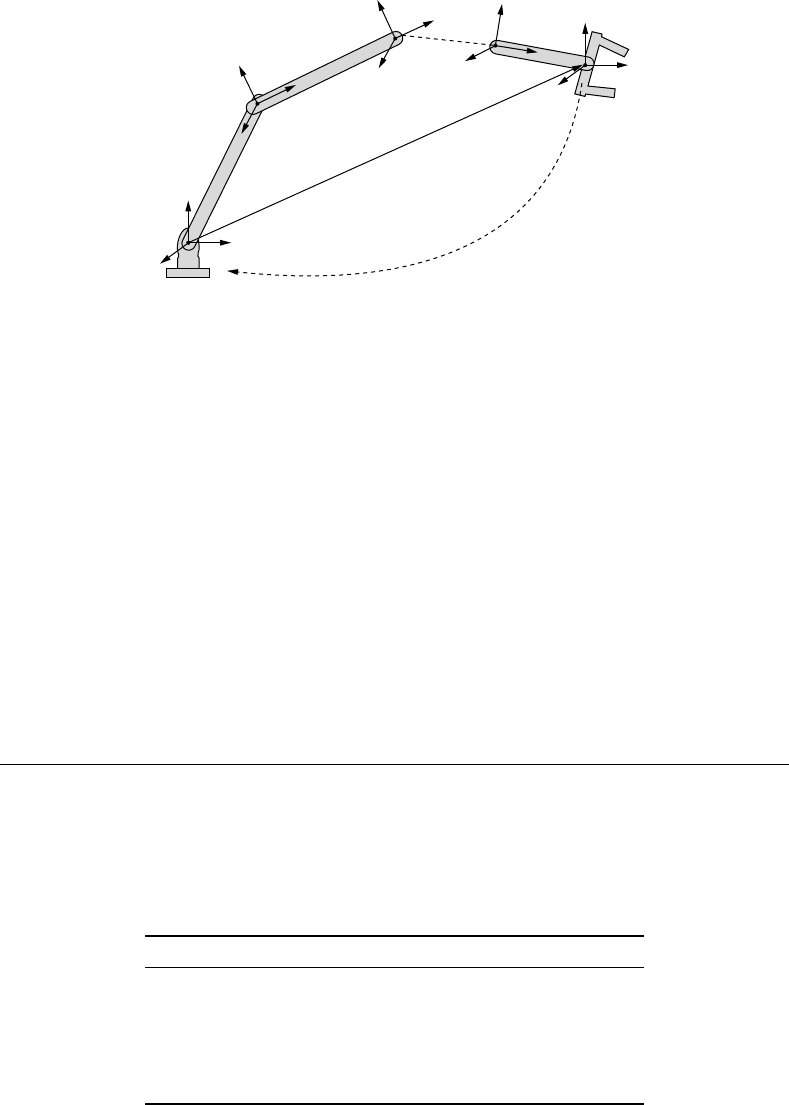
8
-8 Robotics and Automation Handbook
o
0
o
n
o
1
d
0
n
A
0
n
o
2
o
n−1
FIGURE 8.5 Transformation from the endeffector frame to the base frame.
Performing the composition from the nth frame to the base frame (see Figure 8.5), we get
A
0
n
= A
0
1
A
1
2
...A
n−1
n
=
R
0
n
d
0
n
01
(8.23)
Based on Equations (8.20) and (8.23) we can write
R
0
n
= (U
1
V
1
)(U
2
V
2
) ···(U
n
V
n
) (8.24)
and
d
0
n
= U
1
s
1
+U
1
V
1
U
2
s
2
+U
1
V
1
U
2
V
2
U
3
s
3
...+U
1
V
1
U
2
V
2
...U
n−1
V
n−1
U
n
s
n
(8.25)
8.4 Examples
Example 8.1
Figure 8.6 is an example of a robotic arm manipulator with five joints. In this manipulator, three joints
are rotational and two joints are prismatic. Thus, the robot has five degrees of freedom.
No. Twist Angle α
i
Link Length a
i
Joint Offset d
i
Joint Angle θ
i
1
(0−1)
000θ
Va ri ab le
1
2
(1−2)
π/20d
Va ri ab le
2
0
3
(2−3)
π/20 0θ
Va ri ab le
3
4
(3−4)
00d
Va ri ab le
4
0
5
(4−5)
000θ
Va ri ab le
5
The first step in determining the D-H parameters is to locate the joints of the robot arm manipulator
and determine if the joint is prismatic or revolute. For the five-degrees-of-freedom manipulator, starting
from the base joint, joints 1, 3, and 5 are revolute joints, while joints 2 and 4 are prismatic joints. Because
Copyright © 2005 by CRC Press LLC
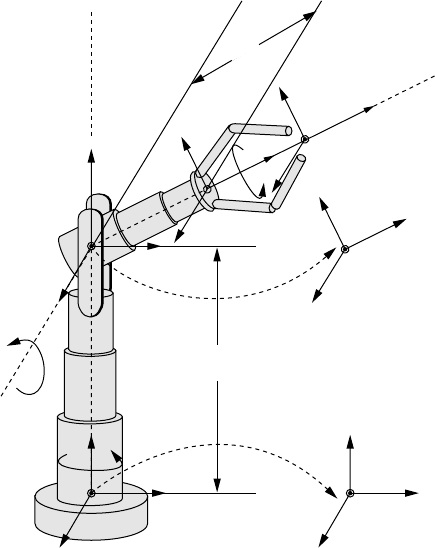
D-H Convention 8
-9
X
1
Z
1
d
2
d
4
X
5
Z
2
Z
5
Z
3
Z
4
X
2
X
0
Y
4
Y
3
Y
1
Y
0
X
3
X
4
Y
2
Y
5
q
5
q
3
q
1
Z
0
FIGURE 8.6 D-H notation for a five-degrees-of-freedom robot arm manipulator.
joints 1, 3, and 5 are revolute, the θ
i
values are variable, i.e., θ
Variable
1
, θ
Variable
3
, and θ
Variable
5
, respectively.
Since there is no rotation about prismatic joints, the θ
i
values for joints 2 and 4 are zero. Similarly for
prismatic joints 2 and 4, the d
i
values are variable, i.e., d
Variable
2
and d
Variable
4
while θ
2
and θ
4
are zero.
As per the flow chart in Figure 8.4, the next step is to set up the joint coordinate frames starting with
the base joint 1. The Z
0
axis points in the direction such that θ
1
is about the Z
0
axis. X
0
and Y
0
are set
up for a right-hand coordinate frame. Joint 2 is a prismatic joint. Thus Z
1
points in the direction of the
translation of the prismatic joint, X
1
is in the plane perpendicular to Z
0
and the direction of Y
1
completes
the right-handed coordinate system. Joint 3 is a revolute joint so the same system follows for assigning
the coordinate frame as the first joint. X
2
lies in the plane perpendicular to Z
2
(and also away from Z
1
).
Similarly the coordinate system for joints 4 and 5 can be assigned as shown in Figure 8.6.
Having established the coordinate frames, the next step is to determine the D-H parameters. We begin
by first determining that α
i
. α
i
is the rotation about X
i
to make Z
i−1
parallel with Z
i
(starting from Z
i−1
).
Starting with axis 1, the rotation about X
1
to make Z
0
parallel with Z
1
is zero because the Z axes for both
are parallel. For axis 2, the rotation required about X
2
to take Z
1
parallel to Z
2
is 90
◦
or π/2. Similarly α
3
is also π/2. Both α
4
and α
5
are zero because the Z axes are parallel for the last two joints.
The next step is to determine a
i
and d
i
. a
i
is the link length and always points away from the Z
i−1
axis.
d
i
is the offset and is always along the Z
i−1
axis. For axis 1, there is no offset in the Z
0
direction from joint
1 to joint 2, so d
1
is equal to zero. Also, the distance between axes 1 and 2 is zero, so a
1
is zero. As seen
from the schematic of the five-degrees-of-freedom manipulator in Figure 8.6, the only nonzero a
i
and d
i
D-H parameters are d
Variable
2
and d
Variable
4
. Each of these distances is in the Z
i−1
direction, so the respective
d values are equal to these distances.
Having determined all the D-H parameters, the transformation matrix A
0
5
can now be computed.
The transformation matrix consists of the rotation matrix R
0
5
and the displacement vector d
0
5
. Using the
Copyright © 2005 by CRC Press LLC
8
-10 Robotics and Automation Handbook
expression in Equation (8.24) and Equation (8.25) we get
R
0
5
= (U
1
V
1
)(U
2
V
2
)(U
3
V
3
)(U
4
V
4
)(U
5
V
5
)
(8.26)
d
0
5
=U
1
s
1
+ (U
1
V
1
)U
2
s
2
+ (U
1
V
1
)(U
2
V
2
)U
3
s
3
+ (U
1
V
1
)(U
2
V
2
)(U
3
V
3
)U
4
s
4
+(U
1
V
1
)(U
2
V
2
)(U
3
V
3
)(U
4
V
4
)U
5
s
5
(8.27)
The following matrices are the individual U and V matrices for each axis of the manipulator.
U
1
=
cos(θ
1
) −sin(θ
1
)0
sin(θ
1
) cos(θ
1
)0
001
, V
1
=
100
010
001
U
2
=
100
010
000
, V
2
=
10 0
00−1
01 0
U
3
=
cos(θ
3
) −sin(θ
3
)0
sin(θ
3
) cos(θ
3
)0
001
, V
3
=
10 0
00−1
01 0
U
4
=
100
010
001
, V
4
=
100
010
001
U
5
=
cos(θ
5
) −sin(θ
5
)0
sin(θ
5
) cos(θ
5
)0
001
, V
5
=
100
010
001
Similarly the s
i
vector is given by
s
1
=
0
0
0
, s
2
=
0
0
d
2
, s
3
=
0
0
0
, s
4
=
0
0
d
4
, s
5
=
0
0
0
Substituting the above U
i
, V
i
, and s
i
into Equation (8.26) and Equation (8.27) we get
R
0
5
=
C
1
C
3
C
5
+ S
1
S
5
−C
1
C
3
S
5
+ S
1
C
5
C
1
S
3
S
1
C
3
C
5
−C
1
S
5
−S
1
C
3
S
5
−C
1
C
5
S
1
S
3
S
3
C
5
−S
3
S
5
−C
3
(8.28)
d
0
5
=
C
1
S
3
d
4
S
1
S
3
d
4
d
2
−C
3
d
4
(8.29)
where C
a
= cos(a) and S
a
= sin(a).
The final transformation matrix is thus given by
A
0
5
=
C
1
C
3
C
5
+ S
1
S
5
−C
1
C
3
S
5
+ S
1
C
5
C
1
S
3
C
1
S
3
d
4
S
1
C
3
C
5
−C
1
S
5
−S
1
C
3
S
5
−C
1
C
5
S
1
S
3
S
1
S
3
d
4
S
3
C
5
−S
3
S
5
−C
3
d
2
−C
3
d
4
0001
(8.30)
Copyright © 2005 by CRC Press LLC
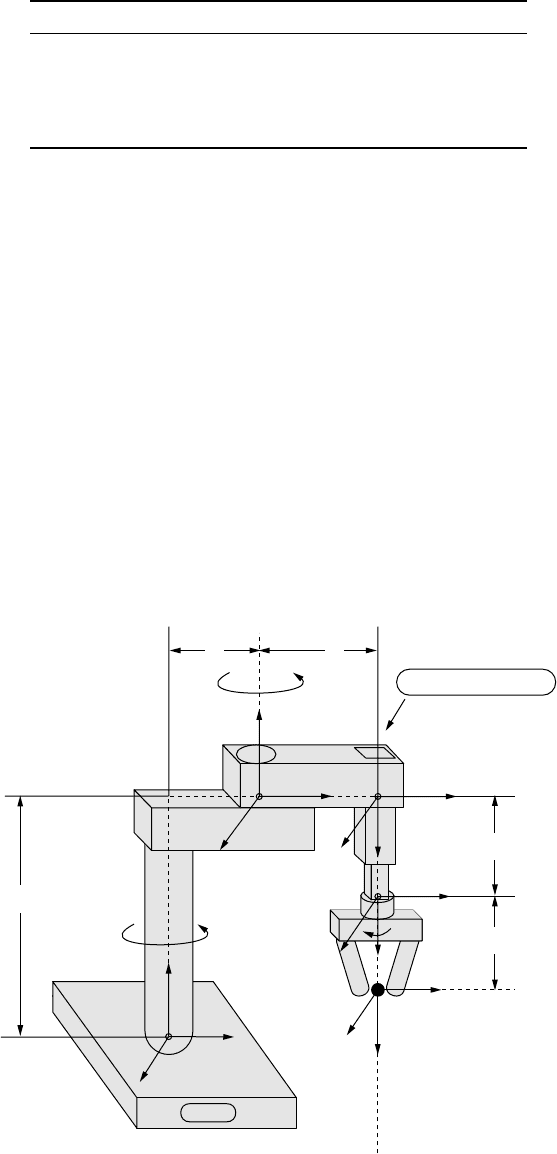
D-H Convention 8
-11
TABLE 8.1 D-H Parameters for the SCARA
No. Twist Angle α
i
Link Length a
i
Link Offset d
i
Joint Angle θ
i
1
(0−1)
0 a
1
d
1
θ
Va ri ab le
1
2
(1−2)
π a
2
0 θ
Va ri ab le
2
3
(2−3)
00d
Va ri ab le
3
0
4
(3−4)
00d
4
θ
Va ri ab le
4
Example 8.2: The SCARA Robot
The SCARA robot is a four axis robot arm manipulator with three revolute joints and one prismatic joint
(see Figure 8.7 and Table 8.1). The name SCARA is an acronym for selective compliance assembly robot arm.
The first step in determining D-H parameters for the SCARA is to locate the joints and determine the
rotation or translation of each joint. The SCARA has four joints with three of them being revolute joints
and one prismatic joint. Each of the revolute joints, 1, 2, and 4, have a θ value of θ
variable
i
with i being the
joint number. The prismatic joint (joint 3) has a θ valueofzeroandad value of d
variable
3
. Starting from the
base, the joint coordinate frames are assigned based on the algorithm outlined before.
Having established the coordinate frames, the next step is the determination of the D-H parameters.
We be gin by first determining α
i
. α
i
is the rotation about X
i
to make Z
i−1
parallel with Z
i
(starting from
Z
i−1
). Starting with axis 1, the rotation about X
1
to make Z
0
parallel to Z
1
is 0 because they are parallel.
For axis 2, the α is π or 180
◦
because Z
2
is pointing down along the translation of the prismatic joint. α
3
and α
4
are zero because Z
3
and Z
4
are parallel with Z
2
and Z
3
, respectively.
The next step is to determine a
i
and d
i
. a
i
is the link length and always points away from the Z
i−1
axis.
d
i
is the offset and is always along the Z
i−1
axis. For axis 1, there is an offset between axes 1 and 2 in the
BASE
PRISMATIC JOINT
d
1
X
1
X
2
X
3
X
4
X
0
Y
1
Y
2
Y
3
Y
4
Y
0
Z
2
Z
3
Z
1
Z
4
Z
0
a
1
a
2
q
2
q
1
q
4
d
4
d
3
FIGURE 8.7 Schematic of the SCARA robot with the appropriate coordinate frames.
Copyright © 2005 by CRC Press LLC
8
-12 Robotics and Automation Handbook
Z
0
direction so the offset is equal to d
1
. There is also a distance between the axes, which is equal to a
1
.For
axis 2, there is a distance between axes 2 and 3 away from the Z
1
axis equal to a
2
. d
2
is equal to zero. Axis
3 is a prismatic joint, so d is variable, i.e., d
Variable
3
. Between axes 3 and 4, there is an offset only in the Z
direction, so d
4
is equal to this distance. a
3
and a
4
are both zero.
Having determined all the D-H parameters, the transformation matrix A
0
4
can now be computed.
The transformation matrix consists of the rotation matrix R
0
4
and the displacement vector d
0
4
. Using the
expression in Equation (8.24) and Equation (8.25) we get
R
0
4
= (U
1
V
1
)(U
2
V
2
)(U
3
V
3
)(U
4
V
4
) (8.31)
d
0
4
= U
1
s
1
+ (U
1
V
1
)U
2
s
2
+ (U
1
V
1
)(U
2
V
2
)U
3
s
3
+ (U
1
V
1
)(U
2
V
2
)(U
3
V
3
)U
4
s
4
(8.32)
The following matrices are the individual U and V matrices for each axis of the manipulator.
U
1
=
cos(θ
1
) −sin(θ
1
)0
sin(θ
1
) cos(θ
1
)0
001
, V
1
=
100
010
001
U
2
=
cos(θ
2
) −sin(θ
2
)0
sin(θ
2
) cos(θ
2
)0
001
, V
2
=
100
0 −10
00−1
U
3
=
100
010
001
, V
3
=
100
010
001
U
4
=
cos(θ
4
) −sin(θ
4
)0
sin(θ
4
) cos(θ
4
)0
001
, V
4
=
100
010
001
Similarly the s
i
vector is given by
s
1
=
a
1
0
d
1
, s
2
=
a
2
0
0
, s
3
=
0
0
d
3
, s
4
=
0
0
d
4
Substituting the above U
i
, V
i
, and s
i
into Equation (8.31) and Equation (8.32) we get
R
0
4
=
C
12
C
4
+ S
12
S
4
−C
12
S
4
+ S
12
C
4
0
S
12
C
4
−C
12
S
4
−S
12
S
4
−C
12
C
4
0
00−1
(8.33)
d
0
4
=
C
1
a
1
+C
12
a
2
S
1
a
1
+ S
12
a
2
d
1
− d
3
− d
4
(8.34)
where C
a
= cos(a), S
a
= sin(a), C
ab
= cos(a + b) and S
ab
= sin(a + b).
The final transformation matrix is
A
0
4
=
C
12
C
4
+ S
12
S
4
−C
12
S
4
+ S
12
C
4
0 C
1
a
1
+C
12
a
2
S
12
C
4
−C
12
S
4
−S
12
S
4
−C
12
C
4
0 S
1
a
1
+ S
12
a
2
00−1 d
1
− d
3
− d
4
0001
(8.35)
Copyright © 2005 by CRC Press LLC
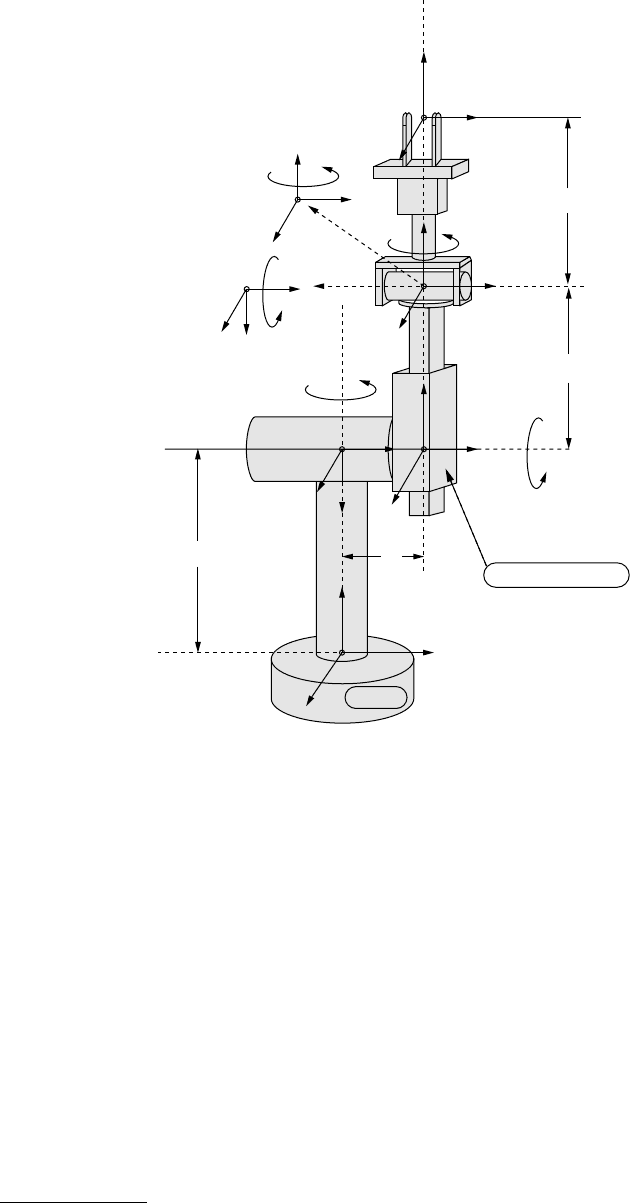
D-H Convention 8
-13
Z
1
d
2
d
1
d
3
d
6
X
5
X
6
Z
1
Z
5
Z
6
Z
3
Z
4
X
2
X
0
Y
4
Y
3
Y
1
Y
0
X
4
Y
2
Y
6
Y
5
q
5
q
6
q
4
q
2
q
1
Z
0
BASE
PRISMATIC JOINT
X
3
Z
2
X
1
FIGURE 8.8 Schematic of the Stanford arm.
Example 8.3: The Stanford Arm
Designed in 1969 by Victor Scheinman, the Stanford arm was one of the first robots exclusively designed
for computer control.
1
The Stanford arm is a 6-axis robot manipulator with five revolute joints and one
prismatic joint, giving it six degrees of freedom
The first step in determining the D-H parameters for the Stanford arm is to locate the joints and
determine if the joint is prismatic or revolute (Table 8.2). Starting from the base joint, joints 1, 2, 4, 5, and
6 are all revolute joints. The θ
i
values are θ
Variable
1
, θ
Variable
2
, θ
Variable
4
, θ
Variable
5
, and θ
Variable
6
, respectively. Since
there is no rotation about prismatic joints, θ
3
is equal to zero but d
3
is equal to d
Variable
3
. Starting from the
base, the joint coordinate frames are assigned based on the algorithm outlined before.
Having established the coordinate frames, the next step is to determine the D-H parameters. We begin
by first determining α
i
. α
i
is the rotation about X
i
to make Z
i−1
parallel with Z
i
. For axis 1, the rotation
required about X
1
to take Z
0
parallel to Z
1
is −90
◦
or −π/2. Similarly α
2
and α
5
are equal to 90
◦
or π/2.
For axes 3 and 6, Z
i−1
and Z
i
are parallel, so α
3
and α
6
are equal to zero.
1
http://www-db.stanford.edu/pub/voy/museum/pictures/display/1-Robot.htm
Copyright © 2005 by CRC Press LLC

8
-14 Robotics and Automation Handbook
TABLE 8.2 D-H Parameters for the Stanford Arm
No. Twist Angle α
i
Link Length a
i
Link Offset d
i
Joint Angle θ
i
1
(0−1)
−π/2 0 d
1
θ
Va ri ab le
1
2
(1−2)
π/20 d
2
θ
Va ri ab le
2
3
(2−3)
00d
Va ri ab le
3
0
4
(3−4)
−π/2 0 0 θ
Va ri ab le
4
5
(4−5)
π/20 0θ
Va ri ab le
5
6
(5−6)
00d
6
θ
Va ri ab le
6
The next step is to determine a
i
and d
i
. a
i
is the link length and always points away from the Z
i−1
axis.
d
i
is the offset and is along the Z
i−1
axis. As seen from the schematic of the Stanford arm, there is no
distance between axes in any other direction besides the Z direction, thus the a
i
for each link is zero.
Having determined all the D-H parameters, the transformation matrix A
0
6
can now be computed.
The transformation matrix consists of the rotation matrix R
0
6
and the displacement vector d
0
6
. Using the
expression in Equation (8.24) and Equation (8.25) we get
R
0
6
= (U
1
V
1
)(U
2
V
2
)(U
3
V
3
)(U
4
V
4
)(U
5
V
5
)(U
6
V
6
) (8.36)
d
0
6
=U
1
s
1
+ (U
1
V
1
)U
2
s
2
+ (U
1
V
1
)(U
2
V
2
)U
3
s
3
+ (U
1
V
1
)(U
2
V
2
)(U
3
V
3
)U
4
s
4
+(U
1
V
1
)(U
2
V
2
)(U
3
V
3
)(U
4
V
4
)U
5
s
5
+ (U
1
V
1
)(U
2
V
2
)(U
3
V
3
)(U
4
V
4
)(U
5
V
5
)U
6
s
6
(8.37)
The following matrices are the individual U and V matrices for each axis of the manipulator.
U
1
=
cos(θ
1
) −sin(θ
1
)0
sin(θ
1
) cos(θ
1
)0
001
, V
1
=
100
001
0 −10
U
2
=
cos(θ
2
) −sin(θ
2
)0
sin(θ
2
) cos(θ
2
)0
001
, V
2
=
10 0
00−1
01 0
U
3
=
100
010
001
, V
3
=
100
010
001
U
4
=
cos(θ
4
) −sin(θ
4
)0
sin(θ
4
) cos(θ
4
)0
001
, V
4
=
100
001
0 −10
U
5
=
cos(θ
5
) −sin(θ
5
)0
sin(θ
5
) cos(θ
5
)0
001
, V
5
=
10 0
00−1
01 0
U
6
=
cos(θ
6
) −sin(θ
6
)0
sin(θ
6
) cos(θ
6
)0
001
, V
6
=
100
010
001
Similarly the s
i
vector is given by
s
1
=
0
0
d
1
, s
2
=
0
0
d
2
, s
3
=
0
0
d
3
, s
4
=
0
0
0
, s
5
=
0
0
0
, s
6
=
0
0
d
6
Copyright © 2005 by CRC Press LLC

D-H Convention 8
-15
Substituting the above U
i
, V
i
, and s
i
into Equation (8.36) and Equation (8.37), we get the following,
where C
i
= cos(i) and S
i
= sin(i):
R
0
6
=
r
11
r
12
r
13
r
21
r
22
r
23
r
31
r
32
r
33
(8.38)
r
11
= ((C
1
C
2
C
4
− S
1
S
4
)C
5
−C
1
S
2
S
5
)C
6
+ (−C
1
C
2
S
4
− S
1
C
4
)S
6
r
12
=−((C
1
C
2
C
4
− S
1
S
4
)C
5
−C
1
S
2
S
5
)S
6
+ (−C
1
C
2
S
4
− S
1
C
4
)C
6
r
13
= (C
1
C
2
C
4
− S
1
S
4
)S
5
+C
1
S
2
C
5
r
21
= ((S
1
C
2
C
4
+C
1
S
4
)C
5
− S
1
S
2
S
5
)C
6
+ (−S
1
C
2
S
4
+C
1
C
4
)S
6
r
22
=−((S
1
C
2
C
4
+C
1
S
4
)C
5
− S
1
S
2
S
5
)S
6
+ (−S
1
C
2
S
4
+C
1
C
4
)C
6
r
23
= (S
1
C
2
C
4
+C
1
S
4
)S
5
+ S
1
S
2
C
5
r
31
= (−S
2
C
4
C
5
−C
2
S
5
)C
6
+ S
2
S
4
S
6
r
32
=−(−S
2
C
4
C
5
−C
2
S
5
)S
6
+ S
2
S
4
C
6
r
33
=−S
2
C
4
S
5
+C
2
C
5
d
0
6
=
d
11
d
21
d
31
(8.39)
d
11
=−S
1
d
2
+C
1
S
2
d
3
+ ((C
1
C
2
C
4
− S
1
S
4
)S
5
+C
1
S
2
C
5
)d
6
d
21
=C
1
d
2
+ S
1
S
2
d
3
+ ((S
1
C
2
C
4
+C
1
S
4
)S
5
+ S
1
S
2
C
5
)d
6
d
31
= d
1
+C
2
d
3
+ (−S
2
C
4
S
5
+C
2
C
5
)d
6
The final transformation matrix is
A
0
6
=
R
0
6
d
0
6
000
1
(8.40)
Example 8.4: The Mitsubishi PA-10 Robot Arm
The Mitsubishi PA-10 robot arm is a 7-joint robot manipulator. All seven of the joints are revolute, and
thus the manipulator has seven degrees of freedom. The first step in determining the D-H parameters of
the Mitsubishi PA-10 robot arm is to locate each joint and determine whether it is rotational or prismatic
(Table 8.3 and Figure 8.9). As seen in Figure 8.9, all the joints are rotational joints. Because all the joints
are rotational the θ
i
values are variable. Starting from the base, the joint coordinate frames are assigned
based on the algorithm outlined before.
TABLE 8.3 D-H Parameters of the Mitsubishi PA-10 Robot Arm
No. Twist Angle α
i
Link Length a
i
Joint Offset d
i
Joint Angle θ
i
1
(0−1)
−π/2 0 0 θ
Va ri ab le
1
2
(1−2)
−π/2 0 0 θ
Va ri ab le
2
3
(2−3)
π/20 d
3
θ
Va ri ab le
3
4
(3−4)
π/20 0θ
Va ri ab le
4
5
(4−5)
π/20 d
5
θ
Va ri ab le
5
6
(5−6)
−π/2 0 0 θ
Va ri ab le
6
7
(6−7)
00d
7
θ
Va ri ab le
7
Copyright © 2005 by CRC Press LLC
