Kurfess T.R. Robotics and Automation Handbook

Подождите немного. Документ загружается.

The Dynamics of

Systems of Interacting

Rigid Bodies

Kenneth A. Loparo

Case Western Reserve University

Ioannis S. Vakalis

Institute for the Protection and Security of

the Citizen (IPSC) European Commission

7.1 Introduction

7.2 Newton’s Law and the Covariant Derivative

7.3 Newton’s Law in a Constrained Space

7.4 Euler’s Equations and the Covariant Derivative

7.5 Example 1: Euler’s Equations for a Rigid Body

7.6 The Equations of Motion of a Rigid Body

7.7 Constraint Forces and Torques between

Interacting Bodies

7.8 Example 2: Double Pendulum in the Plane

7.9 Including Forces from Friction and from

Nonholonomic Constraints

7.10 Example 3: The Dynamics of the Interaction

of a Disk and a Link

7.11 Example 4: Including Friction in the Dynamics

7.12 Conclusions

7.1 Introduction

In this chapter, we begin by examining the dynamics of rigid bodies that interact with other moving or

stationary rigid bodies. All the bodies are components of a multibody system and are allowed to have

a single point of interaction that can be realized through contact or some type of joint constraint. The

kinematics for the case of point contact has been formulated in previous works [52–54]. On the other

hand, the case of joint constraints can be easily handled because the type of joint clearly deﬁnes the de-

grees of freedom that are allowed for the rigid bodies that are connected through the joint. Then we will

introduce a methodology for the description of the dynamics of a rigid body generally constrained by

points of interaction. Our approach is to use the geometric properties of Newton’s equations and Euler’s

equations to accomplish this objective. The methodology is developed in two parts, we ﬁrst investigate

the geometric properties of the basic equations of motion of a rigid body. Next we consider a multibody

system that includes point interaction that can occur through contact or some type of joint constraint.

Each body is considered initially as an independent unit and forces and torques are applied to the bodies

through the interaction points. There is a classiﬁcation of the applied forces with respect to their type

-2 Robotics and Automation Handbook

(e.g., constraint, friction, external). From the independent dynamic equations of motion for each body we

can derive a reduced model of the overall system, exploiting the geometric properties of the physical laws.

The framework that is developed can also be used to solve control problems in a variety of settings. For

example, in addition to each point contact constraint, we can impose holonomic and/or nonholonomic

constraints on individual bodies. Holonomic and nonholonomic constraints have been studied extensively

in the areas of mechanics and dynamics, see, for example [4,37]. Holonomic control problems have been

studied recently in the context of robotics and manipulation, for example [33,34]. On the other hand,

nonholonomic control problems, which are more difﬁcult to solve, have recently attracted the attention of

a number of researchers and an extensive published literature is developing. Speciﬁc classes of problems

have been studied, such as mechanical systems sliding or rolling in the plane, see, for example [9–11].

Another category of nonholonomic control problems deals with mobile robots and wheeled vehicles,

for example [7,8,15,28–31,36,42–48,50,51]. Spacecrafts and space robots are a further class of mechan-

ical systems with holonomic constraints. The reason for this characterization is the existence of certain

model symmetries that correspond to conserved quantities. If these quantities are not integrable, then

we have a nonholonomic problem. A number of works have been published in this area, see, for exam-

ple [16,21,26,35,38,49,55], and the literature in this area is still developing. Important techniques based on

the concept of geometric phases have also been developed for the solution of holonomic control problems

[9,19,27,32,38–40].

7.2 Newton’s Law and the Covariant Derivative

Application of Newton’s law is a very familiar technique for determining the equations of motion for an

object or a particle in three space (IR

). The fact that we use Newton’slawinIR

, which has some nice

geometric properties, disguises the intrinsic geometric aspects of the law. A geometric interpretation of

Newton’s law becomes apparent when we use it in cases where the object or the particle is constrained to

move on a subset Q, or a submanifold M,inIR

. As we have seen from some of our previous work [53],

such submanifolds result when the object is conﬁned to move in contact with other surfaces in IR

, which

can be stationary or moving (other objects). Whenever an object is in contact with a surface in IR

then

we have “reaction” forces as a result of the contact, and three reaction forces are applied to the object and

on the surface. These forces in the classical formulation are vectors vertical to the common tangent plane

between the objects or the object and the surface at the point of contact, and it is necessary to distinguish

these forces from the friction forces that are introduced tangent to the contacting surfaces. The “reaction”

forcesareintroducedinNewton’s formulation of the equations of motion because the object is constrained

to move on a given surface. We begin our development by considering the original form of Newton’slawin

. Assume that there is an object moving in IR

, then Newton’s law states that the acceleration multiplied

by the mass of the object is equal to the applied forces on the object. We can elaborate more on this simple

form of the law so that its geometric aspects become more obvious. This can be done using concepts from

Riemannian geometry in IR

. The kinetic energy metric in IR

, which when expressed in local coordinates

is given by E =

The kinetic energy metric gives a Riemannian structure to IR

, denoted by

·, · : TIR

× TIR

−→ IR and E =

v

, v



Definition 7.1 A Riemannian structure on a manifold N is a covariant tensor k of type T

(N). The

covariant tensor k : TN × TN −→ IR, is nondegenerate and positive deﬁnite.

Nondegenerate and positive deﬁnite mean that k(v

, v

) > 0, ∀v

∈ T

N when v

= 0. In this

chapter we will consider only positive deﬁnite Riemannian metrics. Some of the following deﬁnitions

and theorems are also valid for pseudo-Riemannian metrics [1]. The Riemannian structure is important

because later in the development we will need to induce a metric from one manifold to another manifold

Tensor notation requires superscripts for coordinates instead of subscripts.

The Dynamics of Systems of Interacting Rigid Bodies 7

-3

through an immersion. This requires a positive deﬁnite Riemannian metric on the ﬁrst manifold and the

extension to a pseudo-Riemannian metric requires further investigation and will not be discussed here.

In order to establish a geometric form for the acceleration component of Newton’slaw,weneedtoin-

troduce the notion of a connection on a general Riemannian manifold. The connection is used to describe

the acceleration along curves in more general spaces like a Riemannian manifold, see Boothby [12].

Definition 7.2 A C

∞

connection ∇ on a manifold N is a mapping ∇ : X(N) × X(N) −→ X(N)

deﬁned by ∇(X, Y) −→ ∇

Y,∇ satisﬁes the linearity properties for all C

∞

functions f, g on N and

X, X



, Y, Y



∈ X(N):

1. ∇

fX+gX



Y = f (∇

Y) + g (∇



2. ∇

( fY+ gY



) = f ∇

Y + g∇



+ (Xf)Y + (Xg)Y



Here, X(M) denotes the set of C

∞

vector ﬁelds on the manifold M.

Definition 7.3 A connection on a Riemannian manifold N is called a Riemannian connection if it has

the additional properties:

1. [X, Y ] =∇

Y −∇

2. XY, Y



=∇

Y, Y



+Y, ∇





Here, [·, ·] denotes the Lie bracket.

Theorem 7.1 If N is a Riemannian manifold, then there exists a uniquely determined Riemannian con-

nection on N.

A comprehensive proof of this theorem can be found in W.M. Boothby [12]. The acceleration along a

curve c(t) ∈ N is given by the connection ∇

c(t)

c(t). In this context the Riemannian connection denotes

the derivative of a vector ﬁeld along the direction of another vector ﬁeld, at a point m ∈ N.

To understand how the covariant derivative, deﬁned on a submanifold M of IR

, leads to the abstract

notion of a connection, we need to introduce the derivative of a vector ﬁeld along a curve in IR

. Consider a

vector ﬁeld X deﬁnedonIR

and a curve c(t) ∈ IR

.LetX(t) = X |

c(t)

, then the derivative of X(t) denoted

X(t) is the rate of change of the vector ﬁeld X along this curve. Consider a point c(t

) = p ∈ IR

and the vectors X(t

) ∈ T

c(t

)

and X(t

+ t) ∈ T

c(t

+t)

. We can use the natural identiﬁcation of

c(t

)

with T

c(t

+t)

, and the difference X(t

+t) − X(t

) can be deﬁned in T

c(t

)

. Consequently,

the derivative

X(t

) can be deﬁned by

X(t

) = lim

t→0

X(t

+ t) − X(t

)

t

Consider a submanifold M imbedded in IR

, and a vector ﬁeld X on M, not necessarily tangent to M.

Then, the derivative of X along a curve c(t) ∈ M is denoted by

X(t) ∈ T

c(t)

.Atapointc(t

) = p ∈ M,

the tangent space T

can be decomposed into two mutually exclusive subspaces T

= T

M ⊕T

⊥

Consider the projection p

: T

−→ T

M, the covariant derivative of X along c(t) ∈ M is deﬁned as

follows:

Definition 7.4 The covariant derivative of a vector ﬁeld X on a submanifold M of IR

along a curve

c(t) ∈ M is the projection p

(

X(t)) and is denoted by

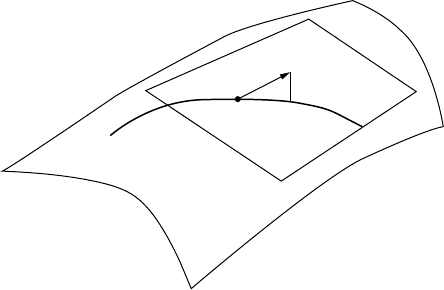
An illustration of the covariant derivative is given in Figure 7.1. The covariant derivative gives rise to

the notion of a connection through the following construction: Consider a curve c(t) ∈ M, the point

p = c(t

),and the tangentvectortothe curve X

c(t

)atp. We can deﬁnethe map ∇

: T

M −→ T

by ∇

Y : X

−→

t=t

, along any curve c(t) ∈ M such that

c(t

) = X

and Y ∈ M. Along the curve

c(t)wehave∇

c(t)

Y =

. The connection can be deﬁned as a map ∇ : X(M)×X(M) −→ X(M), where

-4 Robotics and Automation Handbook

X(t)

c(t)

c(t

)

X(t

+ ∆t)

FIGURE 7.1 The covariant derivative of a vector ﬁeld X.

∇ :(X, Y ) −→ ∇

Y. In a general Riemannian manifold, the connection is deﬁned ﬁrst and then the

covariant derivative is introduced by

=∇

c(t)

Y. In general, the acceleration on a Riemannian manifold

N, along a path c(t), is given by

∇

c(t)

It then follows that the equation for a geodesic curve is given by ∇

c(t)

c(t) = 0.

Consider now a curve c : I −→ IR

, which represents the motion of a body or a particle in IR

Computing the acceleration of the body along this curve provides only one part of the expression needed

for Newton’s law. Because IR

is a Riemannian manifold, the acceleration along a curve is given by the

connection ∇

c(t)

c(t) ∈ TIR

Consequently, we need to examine the geometric properties of the forces applied to the object. As

mentioned previously, the forces in the classical approach are considered as vectors in IR

, but this is not

sufﬁcient for a geometric interpretation of Newton’s law. Geometrically the forces are considered to be

1-forms on the cotangent space associated with the state space of the object, which in our case is T

∗

The main reason that the forces are considered to be 1-forms is because of the concept of “work.” Actually,

the work done by the forces along c(t) is given by the integral of the 1-forms representing the forces that

are acting along c(t).

Although we have provided a geometric interpretation for the acceleration and the forces, there is still a

missing link because the acceleration is a vector ﬁeld on the tangent space TIR

and the forces are 1-forms

on the cotangent space T

∗

. Thus, we cannot just multiply the acceleration by the mass and equate the

product with the forces. The missing link is provided by the kinetic energy metric, using its properties

as a covariant tensor. More speciﬁcally, if we consider a covariant tensor k on a manifold N of the type

(N), then there is a map associated with the tensor called the ﬂat map of k (refer to R. Abraham and

J.E. Marsden [1] for more details). Let k



denote the ﬂat map, deﬁned by

∀v ∈ TN k



(v) = k(v, ·) and k



: TN −→ T

∗

thus k



(v) is a 1-form on T

∗

N. Consider the kinetic energytensor E =

σ (u, u)onIR

, then σ



: TIR

−→

∗

and ∀v ∈ TIR

, σ



(v)isa1-forminT

∗

If we let the ﬂat map of the kinetic energy tensor σ



act on the covariant derivative ∇

c(t)

c(t), we obtain

a 1-form in T

∗

. The geometric form of Newton’s law is then given by



(∇

c(t)

c(t)) = F

(7.1)

where F denotes the 1-forms corresponding to the forces applied on the body.

The Dynamics of Systems of Interacting Rigid Bodies 7

-5

If the body is constrained to move on a submanifold M of IR

, the state space of the object is no longer

but the submanifold M of IR

7.3 Newton’s Law in a Constrained Space

Next, we need to examine how to describe the dynamics of the constrained object on the submanifold

M, instead of IR

.Morespeciﬁcally we want to ﬁnd a description of Newton’s law on the constrained

submanifold M, to develop dynamic models for systems of interacting rigid bodies, with the ultimate

objective of developing control strategies for this class of systems. In order to constrain the dynamic

equation σ



(∇

c(t)

c(t)) = F on the submanifold M, we must constrain the different quantities involved

in Newton’s law; we begin with the restriction of the kinetic energy tensor σ to M.

Consider a smooth map f : N −→ N



,whereN, N



are C

∞

manifolds. Let T



) denote the set of

covariant tensors of order k on N



. Then if  ∈ T



), we can deﬁne a tensor on N in the following way:

∗

: T



) −→ T

(N)

( f

∗

)

, ..., u

) = 

f (p)

( f

∗

, ..., f

∗

)

where

∈ T

Ni= 1, ..., k and f

∗p

: T

N −→ T

f (p)



denotes the derived map of f . The map f

∗

is called the pull-back. Earlier we denoted the dual map of

∗

,by f

∗

. This notation is consistent with that of a pull-back because the dual f

∗

: T

∗

f (p)



−→ T

pulls back 1-forms which are tensors of type T



) and belong to T

∗

f (p)



, to 1-forms in T

∗

N,whichare

tensors of type T

(N).

The pull-back in the algebraic sense can be deﬁned without the further requirement of differentiability,

and the manifold N need not be a submanifold of N



. Next, we examine under what conditions we can

pull-back a covariant tensor on a manifold N and ﬁnd a coordinate expression in the local coordinates of

N. The answer is given by the following theorem from R. Abraham, J. E. Marsden, and T. Ratiu [2]:

Theorem 7.2 Let N and N



be two ﬁnite dimensional manifolds and let f : N −→ N



be a C

∞

map with

a local expression

= f

, ..., x

) i = 1, ..., n in the appropriate charts, where dim(N) = m and

dim(N



) = n. Then, if t is a tensor in T



), the pull-back f

∗

t is a tensor in T

(N) and has the coordinate

expression:

( f

∗

,..., j

∂y

∂x

···

∂y

∂x

,...,k

◦ f

Here ( f

∗

,..., j

and t

,...,k

, denote the components of the tensors f

∗

t and t, respectively. To pull-back

a tensor from a manifold N



to a manifold N requires a C

∞

map f : N −→ N



, with a coordinate

representation y

= f

, ..., x

). There is a certain condition that guarantees that a map between two

manifolds can have a coordinate representation, and thus can be used to pull-back a covariant tensor.

The notion of an immersion is important for the further developement of these ideas (see F. Brickell and

R.S. Clark [13] for more details).

Definition 7.5 Let N



and N be two ﬁnite dimensional differentiable manifolds and f : N −→ N



∞

map, then f is called immersion if for every point a ∈ N rank( f ) = dim(N).

Here we also use tensor notation for the coordinates.

-6 Robotics and Automation Handbook

When studying the dynamics of rigid bodies, we deal with Riemannian metrics, which are tensors of type



). Using the general theorem for pulling back covariant tensors and the deﬁnition of an immersion,

the following theorem results, see F. Brickell and R.S. Clark [13]:

Theorem 7.3 If a manifold N



has a given positive deﬁnite Riemannian metric then any global immersion

f : N −→ N



induces a positive deﬁnite Riemannian metric on N.

A manifold N is a submanifold of a manifold N



if N is a subset of N



and the natural injection

i : N −→ N



is an immersion. Submanifolds of this type are called immersed submanifolds. If in

addition, we restrict the natural injection to be one to one, then we have an imbedded submanifold [13].

There is an alternative deﬁnition for a submanifold where the subset property is not included along

with the C

∞

structure, see W.M. Boothby [12]. In our case, because we are dealing with the constrained

conﬁguration space of a rigid body which is subset of IE(3), it seems more natural to follow the deﬁnition

of a submanifold given by F. Brickell and R.S. Clark [13].

From the previous theorem we conclude that we can induce a Riemannian metric on a manifold N

if there is a Riemannian manifold N



and a map f : N −→ N



, which is an immersion. The manifold

N need not be a submanifold of N



. In general, N will be a subset of N



and the map f : N −→ N



needed to induce a metric. We consider a system of rigid bodies with each body of the system as a separate

unit moving in a constraint state space because of the presence of some joint or point contact beween it

and the rest of the bodies. The case of a joint constraint is easier to deal with because the type of joint

also deﬁnes the degrees of freedom of the constrained body. The degrees of freedom then deﬁne the map

that describes the constrained conﬁguration space of motion as a submanifold of IE(3). Accordingly we

can then induce a Riemannian metric on the constrained conﬁguration space. The case of point contact

is more complicated. We have studied the problem of point contact, where the body moves on a smooth

surface B in [53]. In this work we have shown that the resulting constrained conﬁguration space M is a

subset of IE(3). M is also a submanifold of IE(3) × B and there is a map µ

: M −→ IE(3). This map is

not necessarily the natural injection i : M −→ IE(3). The map µ

therefore should be an immersion so

that it induces a Riemannian metric on M from IE(3). This is not generally the case when we deal with the

dynamics of constrained rigid body motions deﬁned by point contact.

Using this analysis we can now study the geometric form of Newton’s law for bodies involved in

constrained motion. To begin with we need to endow the submanifold M of IR

with a Riemannian

structure. According to the discussion above this is possible using the pull-back of the Riemannian metric

σ on IR

through the natural injection j : M −→ IR

,where j is by deﬁnition an immersion. We let

σ = j

∗

σ denote the induced Riemannian structure on the submanifold M by the pull-back j

∗

. We can

explicitly compute the coordinate representation of the pull-back of the Riemannian metric

σ if we use the

fact that positive deﬁnite tensors of order T



) on a manifold N



can be represented as positive deﬁnite

symmetric matrices. In our case, the Riemannian metric in IR

can be represented as a 3 × 3 positive

deﬁnite symmetric matrix given by

σ =













Assume that the submanifold M is two-dimensional and has coordinates {x

, x

}, and {y

, y

} are the

coordinates of IR

. Then, the derived map j

∗

: TM −→ TIR

has the coordinate representation:

∗







∂ j

∂x

∂ j

∂x

∂ j

∂x

∂ j

∂x

∂ j

∂x

∂ j

∂x







The Dynamics of Systems of Interacting Rigid Bodies 7

-7

The induced Riemannian metric

σ on M (by using the pull-back) has the following coordinate

representation:

σ = j

∗

σ =



∂ j

∂x

∂ j

∂x

∂ j

∂x

∂ j

∂x

∂ j

∂x

∂ j

∂x





















∂ j

∂x

∂ j

∂x

∂ j

∂x

∂ j

∂x

∂ j

∂x

∂ j

∂x







In a similar way we can pull-back 1-forms from T

∗



to T

∗

N, considering that 1-forms are actually

tensors of order T



). We can represent a 1-form ω in the manifold N



, with coordinates {y

, ..., y

as ω = a

+···+a

. Then using the general form for a tensor of type T



), the pull-back of ω

denoted by

ω = f

∗

ω, has the coordinate representation:

ω =







∂ f

∂x

···

∂ f

∂x

∂ f

∂x

···

∂ f

∂x



















where f = f

, ..., f

is the coordinate representation of f and {x

, ..., x

} are the coordinates of N.

Using this formula we can “pull-back” the 1-forms that represent the forces acting on the object. Thus on

the submanifold M, the forces acting on the object are described by

F = j

∗

F . If, for example, we consider

the case where M is a two-dimensional submanifold of IR

, then the 1-form representing the forces applied

on the object F = F

+ F

is pulled back to

F = j

∗

F =



∂ j

∂x

∂ j

∂x

∂ j

∂x

∂ j

∂x

∂ j

∂x

∂ j

∂x















Next we use the results from tensor analysis and Newton’s law to obtain the dynamic equations of a rigid

body on the submanifold M.InNewton’s law the ﬂat map σ



, resulting from the Riemannian metric σ ,

is used. A complete description of the various relations is given by the commutative diagram

TIK

T*IK

TM T*m

Let

c = c |

denote the restriction of the curve c(t)toM.Let

∇ denote the connection on M associated

with the Riemannian metric

σ . Then we can describe Newton’slawonM by



(

∇

c(t)

c(t)) =

(7.2)

We have to be careful how we interpret the different quantities involved in the constrained dynamic

equation above, because the notation can cause some confusion. Actually, the way we have written

-8 Robotics and Automation Handbook



= j

∗

(σ



◦ j

∗

), j

∗

is the pull-back of the 1-form σ



◦ j

∗

. In contrast with the formula,

σ = j

∗

σ ,

where j

∗

is the pull-back of the tensor σ . Actually it is true that



= ( j

∗

σ )



= j

∗

(σ



◦ j

∗

The dynamic Equations (6.2) describe the motion of the object on the submanifold M. The main

advantage of the description of the dynamics of the body on M is that we obtain a more convenient model

of the system for analysis and control purposes.The “reaction” forcesthat wereintroduced asa consequence

of the constraint do not appear explicitly in the model. In the modiﬁed 1-forms, that represent the forces

on the constraint submanifold M denoted by

F = j

∗

F , the “reaction” forces belong to the null space of

∗

.The“reaction” forces act in directions that tend to separate the rigid body from the constraint, and they

do not belong to T

∗

M. The classical argument that the “reaction” forces do no work along the constrained

path

c(t) gives another justiﬁcation for this result [6]. In the case of contact between a rigid body and a

surface, the constraint submanifold M of the rigid body is a submanifold of IE(3) × B. The argument that

no work is done along the path

c(t) holds for the case where the surface that the body moves in contact

with is stationary. In the case of a dynamic system that consists of two contacting bodies where the contact

surface is moving, the argument is that the “reaction” forces do exactly the same amount of work, but with

opposite signs. In this case, of course, we have to consider the dynamic equations of both bodies as one

system [20]. As we are going to see in the next section, the reduction of the dynamic equations to describe

motion on the submanifold M, in the case of contact, also involves the description of Euler’s equations

written in geodesic form.

7.4 Euler’s Equations and the Covariant Derivative

In order to have a complete description of the dynamic equations that determine the behavior of a rigid

body in IR

, we have to consider Euler’s equations also. This set of differential equations was discovered

by Euler in the 18th century and describes the rotational motion of a rigid body. The original form of the

equations is given by

+ (I

− I

)ω

= M

+ (I

− I

)ω

= M

+ (I

− I

)ω

= M

where ω

, ω

are the rotational velocities around each axis of a coordinate frame attached to the body.

This coordinate frame is moving along with the body and is chosen such that the axes are coincident with

the principal axes of the body. Thus I

, I

, and I

are the principle moments of inertia. Finally M

, M

and M

are the external torques applied around each of these axes.

Euler’s representation of the rotational dynamics, although it has a very simple form, comes with two

major disadvantages. The ﬁrst is that the equations are described in body coordinates and if we try to

solve the equations for ω

, ω

, and ω

we have no information about the orientation of the body. This is

a consequence of the fact that there is no reference frame, with respect to which the angular orientation

of the bodies can be measured. The second disadvantage is that this form of Euler’s equations obscures

the fact that they have the form of a geodesic on SO(3); SO(3) is the space of rotations of a rigid body in

(IR

). The geodesic form of Euler’s equations was discussed by V.I. Arnold in [5]. In this work V.I. Arnold

shows that Euler’s equations in their original form are actually described using the local coordinates of

so(3); here so(3) is the Lie algebra corresponding to SO(3) and is also the tangent space of SO(3) at the

identity element. The main idea is to use the exponential map in order to identify the tangent space of a

group G at the identity T

G, with the group (G) itself. The following deﬁnition of the exponential map is

based on notions of the ﬂow of a vector ﬁeld and left invariant vector ﬁelds on a group, see, for example,

Boothby [12] or Brickell and Clark [13]:

Definition 7.6 Consider a group G and a left invariant vector ﬁeld X on G.Wedenoteby :

IR ×G −→ G the ﬂow of X which is a differentiable function. For every v ∈ T

G, there is a left invariant

vector ﬁeld X on G such that X

= v. Then the exponential map exp : T

G −→ G is deﬁned by

v → (1, e).

The Dynamics of Systems of Interacting Rigid Bodies 7

-9

g(t)

Φ(1, e)

FIGURE 7.2 The action of the exponential map on a group.

Where (1, e) is the result of the ﬂowofavectorﬁeld X applied on the identity element e for t = 1.

Figure 7.2 illustrates how the exponential map operates on elements of a group G.

Consider the tangent space of the Lie group G at the identity element e, denoted by T

G. The Lie

algebra of the Lie group G is identiﬁed with T

G, and it can be denoted by V. The main idea underlying

this analysis is the fact that we can identify a chart in V, in the neighborhood of 0 ∈ V, with a chart in the

neighborhood of e ∈ G.Morespeciﬁcally, what V.I. Arnold proves in his work is that Euler’s equations

for a rigid body are equations that describe geodesic curves in the group SO(3), but they are described in

terms of coordinates of the corresponding Lie algebra so(3). This is done by the identiﬁcation mentioned

above using the exponential map exp : so(3) −→ SO(3). We are going to outline the main concepts and

theorems involved in this construction. A complete presentation of the subject is included in [5]. A Lie

group acts on itself by left and right translations. Thus for every element g ∈ G, we have the following

diffeomorphisms:

: G −→ G, L

h = gh

: G −→ G, R

h = hg

As a result, we also have the following maps on the tangent spaces:

g∗

: T

G −→ T

G, R

g∗

: T

G −→ T

Next we consider the map R

−1

: G −→ G, which is a diffeomorphism on the group. Actually, it is

an automorphism because it leaves the identity element of the group ﬁxed. The derived map of R

−1

going to be very useful in the construction which follows:

= (R

−1

)

e∗

: T

G = V −→ T

G = V

Thus, Ad

is a linear map of the Lie algebra V to itself. The map Ad

has certain properties related to

the Lie bracket [·, ·] of the Lie algebra V. Thus, if exp : V −→ G and g (t) = exp( f (t)) is a curve on G,

then we have the following relations:

exp( f (t))

ξ = ξ + t[ f, ξ ] +o(t

)(t → 0)

[ξ, n] = [Ad

ξ, Ad

There are two linear maps induced by the left and right translations on the cotangent space of G, T

∗

These maps are the duals to L

g∗

and R

g∗

and are known as pull-backs of L

and R

, respectively:

∗

: T

∗

G −→ T

∗

G, R

∗

: T

∗

G −→ T

∗

-10 Robotics and Automation Handbook

We have the following properties for the dual maps:

∗

ξ, n) = (ξ, L

g∗

∗

ξ, n) = (ξ, R

g∗

for ξ ∈ T

∗

G, n ∈ T

G. Here, (ξ, n) ∈ IR is the value of the linear map ξ applied on the vector ﬁeld n, both

evaluated at g ∈ G. In general we can deﬁne a Euclidean structure on the Lie algebra V via a symmetric

positive deﬁnite linear operator A : V −→ V

∗

(A : T

G −→ T

∗

G), (Aξ, n) = (An, ξ) for all ξ, n ∈ V.

Using the left translation we can deﬁne a symmetric operator A

: T

G −→ T

∗

G according to the relation

ξ = L

∗

−1

∗

ξ. Finally, via this symmetric operator we can deﬁneametriconT

G by

ξ, n

= (A

n, ξ ) = (A

ξ, n) =n, ξ 

for all ξ, n ∈ T

G. The metric ·, ·

is a Riemannian metric that is invariant under left translations. At the

identity element e, we denote the metric on T

G = V by ·, ·.Wecandeﬁne an operator B : V×V −→ V

using the relation [a, b], c=B(c, a), b for all b ∈ V. B is a bilinear operator, and if we ﬁx the ﬁrst

argument, B is skew symmetric with respect to the second argument:

B(c, a), b+B(c, b), a=0

In the case of rigid body motions the group is SO(3) and the Lie algebra is so(3), but we are going to

keep the general notation in order to emphasize the fact that this construction is more general and can

be applied to a variety of problems. The rotational part of the motion of a body can be represented by a

trajectory g (t) ∈ G.Thus

g represents the velocity along the trajectory

g ∈ T

g(t)

G. The rotational velocity

with respect to the body coordinate frame is the left translation of the vector

g ∈ G to T

G = V. Thus, if

we denote the rotational velocity of the body with respect to the coordinate frame attached to the body by

, then we have ω

= L

−1

∗

g ∈ V. In a similar manner the rotational velocity of the body with respect

to an inertial (stationary) frame is the right translation of the vector

g ∈ T

g(t)

G to T

G = V, which we

denote by ω

= R

−1

∗

g ∈ V.

In this case we have that A

: T

G −→ T

∗

G is an inertia operator. Next, we denote the inertia

operator at the identity by A : T

G −→ T

∗

G. The angular momentum M = A

g ∈ V can be expressed

with respect to the body coordinate frame as M

= L

∗

M = Aω

and with respect to an inertial frame

= R

∗

M = Ad

∗

−1

M (Ad

∗

−1

is the dual of Ad

−1

∗

Euler’s equations according to the notation established above are given by

dω

= B(ω

, ω

), ω

= L

−1

∗

This form of Euler’s equations can be derived in two steps. Consider ﬁrst a geodesic g (t) ∈ G such that

g(0) = e and

g(0) = ω

. Because the metric is left invariant, the left translation of a geodesic is also a

geodesic. Thus the derivative

dω

depends only on ω

and not on g.

Using the exponential map, we can consider a neighborhood of 0 ∈ V as a chart of a neighborhood of

the identity element e ∈ G. As a consequence, the tangent space at a point a ∈ V, namely T

V, is identiﬁed

naturally with V. Thus the following lemma can be stated.

Lemma 7.1 Consider the left translation L

exp(a)

for a ∈ V. This map can be identiﬁed with L

for

a→0. The corresponding derived map is denoted by L

∗a

, and L

∗a

: V = T

V → V = T

V.Ifξ ∈ V

then

a∗

ξ = ξ +

[a, ξ ] + o(a

)

Because geodesics can be translated to the origin using coordinates of the algebra V, the derivative

dω

gives the Euler equations. The proof of the lemma as well as more details on the rest of the arguments can

be found in [5].