Kurfess T.R. Robotics and Automation Handbook
Подождите немного. Документ загружается.


The Dynamics of Systems of Interacting Rigid Bodies 7
-21
Next ξ
∗
is calculated:
ξ
∗
=
10 0 0
00 0 0
01 0 0
00 1 0
tan(
˜
θ
2
)0−tan(
˜
θ
2
)
˜
z
1
−
˜
y
1
+sin(
˜
θ
2
)
cos(
˜
θ
2
)
00 0 1
We can easily see that the map ξ is an immersion, because the rank(ξ
∗
) = 4. Applying ξ
∗
to the 1-forms
of the forces and the torques on the RHS of the dynamic equations, we obtain
ξ
∗
(F + T) =
−m
2
gtan(
˜
θ
2
)
0
m
2
gtan(
˜
θ
2
)
−
˜
z
1
−
˜
y
1
+sin(
˜
θ
2
)
cos(
˜
θ)
2
m
2
g + u
2
We observe that all the reaction forces have disappeared from the model because the complete model
is defined on the constraint submanifold M
1
× M
2
. Thus, we could have neglected them in the initial
modeling of the individual interacting bodies. Special attention should be paid to include the frictional
forces and torques that might occur at the points of interaction (see Example 4).
The kinetic energy tensor ρ has a matrix representation:
ρ =
m 00 0 0 0
0 m 00 0 0
00I 000
000m
2
00
0000m
2
0
0000 0I
2
and we can compute
¯
ρ = ξ
∗
ρ:
¯
ρ =
m
2
tan(
˜
θ
2
)
2
+ m 0 −m
2
tan(
˜
θ
2
)
2
˜
z
1
−
˜
y
1
+sin(
˜
θ
2
)
cos(
˜
θ
2
)
2
m
2
tan(
˜
θ
2
)
0 I 00
−m
2
tan(
˜
θ
2
)
2
0 m
2
tan(
˜
θ
2
)
2
+ m
2
−
˜
z
1
−
˜
y
1
+sin(
˜
θ
2
)
cos(
˜
θ
2
)
2
m
2
tan(
˜
θ
2
)
˜
z
1
−
˜
y
1
+sin(
˜
θ
2
)
cos(
˜
θ
2
)
2
m
2
tan(
˜
θ
2
)0−
˜
z
1
−
˜
y
1
+sin(
˜
θ
2
)
cos(
˜
θ
2
)
2
m
2
tan(
˜
θ
2
)
(
˜
z
1
−
˜
y
1
+sin(
˜
θ
2
))
2
cos(
˜
θ
2
)
4
m
2
+ I
2
7.11 Example 4: Including Friction in the Dynamics
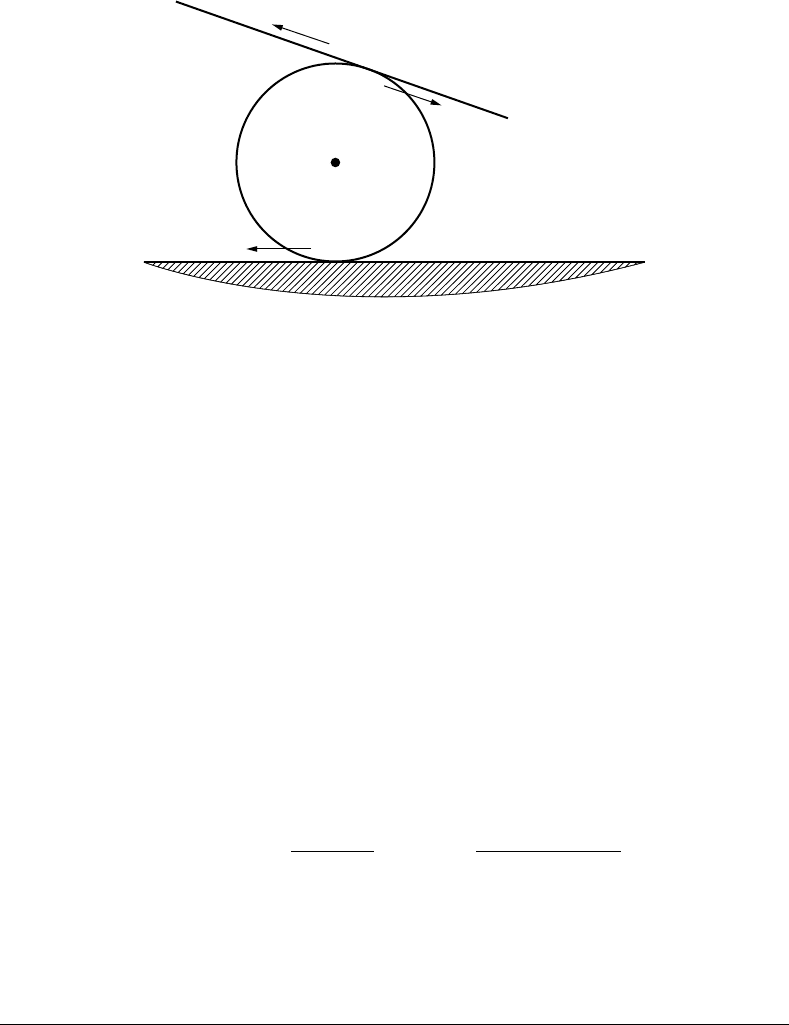
In Example 2 we did not include the friction forces that can occur at the points of contact. If we introduce
friction at the points of contact (Figure 7.6), we have to include these forces in the dynamics as additional
components of the 1-forms representing the forces and torques. When we describe the dynamics of the
disk and the link on the constraint manifolds M
1
and M
2
, respectively, the resulting forces and torques
must include the friction, which affects only the RHS of the dynamic equations.
Copyright © 2005 by CRC Press LLC
7
-22 Robotics and Automation Handbook
–f
1
f
1
f
2
FIGURE 7.6 Friction forces as a result of contact.
Thus the friction forces f
1
and f
2
are included in the 1-forms representing the forces and the torques,
and the RHS of Newton’s and Euler’s equations is given by
−vsin(θ
2
) + f
1
cos(θ
2
) − f
2
u − vcos(θ
2
) −mg − f
1
sin(θ
2
)
− f
1
− f
2
vsin(θ
2
) − f
1
cos(θ
2
)
vcos(θ
2
) −m
2
g + f
1
sin(θ
2
)
0
Here the friction forces contribute to both the forces and torques, as we mentioned above. If we want to
describe the dynamics on the product manifold, M
1
× M
2
, we pull-back this 1-form to obtain
ξ
∗
(F + T) =
−m
2
gtan(
˜
θ
2
) + f
1
sin(
˜
θ
2
) tan(
˜
θ
2
) + f
1
cos(
˜
θ
2
) − f
2
− f
2
− f
1
m
2
gtan(
˜
θ
2
) − f
1
sin(
˜
θ
2
) tan(
˜
θ
2
) − f
1
cos(
˜
θ
2
)
−
˜
z
1
−
˜
y
1
+sin(
˜
θ
2
)
cos(
˜
θ)
2
m
2
g + u
2
+
f
1
sin(
˜
θ
2
)(
˜
z
1
−
˜
y
1
+sin(
˜
θ
2
))
cos
2
(
˜
θ
2
)
As we can see, the friction forces affect the dynamics of the system of interacting bodies on the constraint
submanifold M
1
× M
2
, in contrast to the reaction forces which disappear. The LHS of the dynamic
equations on M
1
× M
2
is unchanged from before.
7.12 Conclusions
In this chapter we have presented a method for the description of the dynamics of a multibody system
where individual elements of the system interact through point contact or through a joint. The modeling
methodology uses results from Differential Geometry to develop a systemtic procedure for deriving a
reduced configuration space and the equations for the system dynamics. The method can be viewed as
an extention to the method proposed by Kron described in B. Hoffmann [20]. Based on this modeling
method, we can restrict the configuration space of a multibody system and, at the same time, exclude
the interaction forces and torques. The resulting constrained model is appropriate for the investigation of
simulation and control of multibody systems, and other related problems.
Copyright © 2005 by CRC Press LLC
The Dynamics of Systems of Interacting Rigid Bodies 7
-23
References
[1] Abraham, R. and Marsden, J.E. (1985). Foundations of Mechanics. Addison-Wesley, Reading, MA.
[2] Abraham, R., Marsden, J.E., and Ratiu, T. (1988). Manifolds, Tensor Analysis and Applications.
Applied Mathematical Sciences. Springer-Verlag, Heidelberg.
[3] Armstrong-Helouvry, B., Dupont, P., and Canudas de Wit, C. (1994). A survey of models, analysis
tools and compensation methods for the control of machines with friction. Automatica, 30, 7,
1083–1038.
[4] Arnold, V.I., Kozlov, V.V., and Neishtadt, A.I. (1988). Mathematical Aspects of Classical and Celestial
Mechanics. Springer-Verlag, Vol. 3.
[5] Arnold, V.I. (1966). Sur la Geometrie Differentielle des Groupes de Lie de Dimension Infinie
et ses Applications a l’ Hydrodynamique des Fluides Parfait. Ann. Inst. Fourier. Grenoble 16, 1,
319–361.
[6] Arnold, V.I. (1978). Mathematical Methods of Classical Mechanics. Springer-Verlag, Heidelberg.
[7] Barraquand, J. and Lacombe, J.C. (1989). On nonholonomic mobile robots and optimal maneuver-
ing. Proceedings of the IEEE International Symposium on Intelligent Control, 25–26 September 1989,
pp. 340–347.
[8] Barraquand, J. and Lacombe, J.C. (1991). Nonholonomic multibodv mobile robots: Controllability
and motion planning in the presence of obstacles. Proceedings of the IEEE International Conference
on Robotics and Automation, 2328–2335.
[9] Bloch, A. , Reyhanoglu, M, and McClamroch, N.H. (1992). Control and stabilization of nonholo-
nomic dynamic systems.” IEEE Transactions on Automatic Control, 37, Il, 1746–1757.
[10] Bloch, A. and McClamroch, N.H. (1989). Control of mechanical systems with classical nonholo-
nomic constraints. Proceedings of the 28th IEEE Conference on Decision and Control, 201–205.
[11] Bloch, A., McClamroch, N.H., and Reyhanoglu M. (1990). Controllability and stabilizability of a
nonholonomic control system. Proceedings of the 29th IEEE Cotiference on Decision and Control,
1312–1314.
[12] Boothby, W.M. (1986). An Introduction to Differentiable Manifolds and Riemannian Geometry.
Academic Press, New York.
[13] Brickell, F. and Clark, R.S. (1970). Differentiable Manifolds. Van Nostrand Reinhold.
[14] Burke, W. (1976). Applied Differential Geometry. Cambridge University Press, Cambridge.
[15] Canudas de Wit, C. and Sordalen, O.J. (1992). Exponential stabilization of mobile robots with
nonholonomic constraints. IEEE Transactions on Automatic Control, 13, 11, 1791–1797.
[16] Chen, C.K. and Sreenath , N. (1993). Control of coupled spatial two-body systems with nonholo-
nomic constraints. Proceedings of the 32nd IEEE Conference on Decision and Control, 949–954.
[17] Goldstein, B. (1944). Mechanics. Quart. Appl. Math., 2, 3, 218–223.
[18] Greenwood, D.T. (1965). Principles of Dynamics. Prentice Hall, NJ, 229–274.
[19] Gurvits, L. and Li, Z. (1993). Smooth time-periodic feedback solutions for nonholonomic motion
planning. In: Nonholonomic Motion Planning, Z. Li and J. Canny, eds, Kluwer, Dordretch, 53–108.
[20] Hoffmann, B. (1944). Kron’s Method of Subspaces. Quart. Appl. Math., 2, 3, 218–223.
[21] Hussein, N.M. and Kane, T.R. (1994). Three dimensional reorientation maneuvers of a system of
interconnected rigid bodies. J. Astron. Sci., 42, 1, 1–25.
[22] Kozlov, V.V. (1982). Dynamical systems with nonintegrable restrictions I. (Engls. Transl.). Mosc.
Univ. Mech. Bull., 37, 3–4, 27–34.
[23] Kozlov, V.V. (1982). Dynamical systems with nonintegrable restrictions II. (Engls. Transl.). Mosc.
Univ. Mech. Bull., 37, 3–4, 78–80.
[24] Kozlov, V.V. (1983). Dynamical systems with nonintegrable restrictions III. (Engls. Transl.). Mosc.
Univ. Mech. Bull., 38, 3, 27–34.
[25] Kozlov, V.V. (1983). Realization of nonintegrable constraints in classical mechanics. (Engls. Transl.).
Soviet Phys. Dokl., 28, 9, 735–737.
[26] Krishnaprasad, P.S. and Yang, R. (1991). Geometric phases, anholonomy, and optimal movement.
Proceedings of the IEEE International Conference on Robotics and Automation, 2185–2189.
Copyright © 2005 by CRC Press LLC
7
-24 Robotics and Automation Handbook
[27] Krishnaprasad, P. S., Yang, R., and Dayawansa, W.P. (1991). Control problems on principle bundles
and nonholonomic mechanics. Proceedings of the 30th IEEE Conference on Decision and Control,
1133–1137.
[28] Latombe, J.-C. (1991). Robot Motion Planning. Kluwer, Boston.
[29] Laumond, J.-P. (1993). Controllability of a multibody mobile robot. IEEE Transactions on Robotics
and Automation, 9, 6, 755–763.
[30] Laumond, J.-P., Jacobs, P.E.,Taix, M., and Murray, R.M. (1994). A motion planner for nonholonomic
systems. IEEE Transactions on Robotics and Automation, 10, 5, 577–593.
[31] Laumond, J.-P., Sekhavat, S., and Vaisset, M. (1994). Collision-free motion planning for a nonholo-
nomic mobile robot with trailers. Proceedings of the IFAC Symposium on Robot Control, Capri, Italy.
[32] Marsden, J.E. (1992). Lectures on mechanics. London Mathematical Society Lecture Notes Series,
174, Cambridge University Press, Cambridge.
[33] McClamroch, N.H. and Bloch, A.M. (1988). Control of constrained Hamiltonian systems and
applications to control of constrained robots. In: Dyanmical Systems Approaches to Nonlin-
ear Problems in Systems and Control, F.M.A. Salam and M.L. Levi, eds, SIAM, Philadelphia,
394–403.
[34] McClamroch, N.H. and Wang, D. (1988). Feedback stabilization and tracking of constrained
robots. IEEE Trans. Automat. Contr., 33, 419–426.
[35] McNally, P.J. and McClamroch, N.H. (1993). Space station attitude disturbance arising from
internal motions. Proceedings of the American Control Conference, 2489–2493.
[36] Murray, R.M., Li, Z., and Sastry, S.S. (1994). A Mathematical Introduction to Robotic Manipulation.
CRC Press, Bota Raton, FL.
[37] Neimark, Y. and Fufaev, N.A. (1972). Dynamics of Nonholonomic Systems. Am. Math. Soc. Transl.,
vol. 33.
[38] Reyhanoglu, M. and McClamroch, N.H. (1992). Planar reorientation maneuvers of space multibody
spacecraft using internal controls. J. Guidance Control Dynamics, 15, 6, 1475–1430.
[39] Reyhanoglu, M. and AI-Regib, E. (1994). Nonholonomic motion planning for wheeled mobile
systems using geometric phases. Proceedings of the 9th IEEE International Symposium on Intelligent
Control, Columbus, Ohio, 135–140.
[40] Reyhanoglu, M., McClamroch, N.H., and Bloch, A.M. (1993). Motion planning for nonholonomic
dynamic systems. In: Nonholonomic Motion Planning, Z. Li and J. F. Canny, eds, Kluwer, Dordretch,
201–234.
[41] Rosenberg, M.R. (1977). Analytical Dynamics of Discrete Systems. Plenum Press, New York,
239–243.
[42] Sahai, A., Secor, M., and Bushnell, L. (1994). An obstacle avoidance algorithm for a car pulling
many trailers with kingpin hitching. Proceedings of the 33rd IEEE Conference on Decision and
Control, 2944–2949.
[43] Samson, C. (1991). Velocity and torque feedback control of a nonholonomic cart. Advanced Robot
Control, C. Canudas de Wit, ed., LNCIS 162, Springer-Verlag, Germany, 125–151.
[44] Samson, C. (1993). Time-varying feedback stabilization of a car-like wheeled mobile robot. Int. J.
Robotics Res., 12, 1, 55–66.
[45] Samson, C. and Ait-Abderrahim, K. 1991. Feedback stabilization of a nonholonomic wheeled
mobile robot. Proceedings of International Conference on Intelligent Robots and Systems (IROS).
[46] Samson, C. (1995). Control of chained system: Application to path following and time-varying
point-stabilization of mobile robots. IEEE Transactions on Automatic Control, 40, 1, 64–77.
[47] Sordalen, O.J. and Wichlund, K.Y. (1993). Exponential stabilization of a car with n trailers.
Proceedings of the 32nd IEEE Control and Decision Conference, 1, 978–983.
[48] Sordalen, O.J. (1993). Conversion of the kinematics of a car with n trailers into a chained form.
Proceedings of the IEEE International Conference on Robotics and Automation, 382–387.
[49] Sreenath, N. (1992). Nonlinear control of planar multibody systems in shape space. Math. Control
Signals Syst., 5, 4, 343–363.
Copyright © 2005 by CRC Press LLC
The Dynamics of Systems of Interacting Rigid Bodies 7
-25
[50] Tilbury, D., Laumond, J.-P., Murray, R., Sastry, S.S., and Walsh, G.C. (1992). Steering, car-like
systems with trailers using sinusoids. Proceedings of the IEEE International Conference on Robotics
and Automation, 2, 1993–1998.
[51] Tilbury, D., Murray, R., and Sastry, S.S. (1993). Trajectory, generation for the N-trailer problem using
Goursat normal form. Proceedings of the 32nd IEEE Conference on Decision and Control, 971–977.
[52] Vakalis, J.S. (1995). Conditions for point contact between robot arm and an object for manipulation
modelling and control. Stud. Informatics Control, 7, 2, 107–127.
[53] Vakalis, J.S. and Loparo, K. (1996). Configuration space of a body moving on a surface and the
kinematics of rolling. Int. J. Engng. Sci., 34, 7, 831–850.
[54] Vakalis, J.S. (1990). “Kinematic and dynamic modelling of interacting manybody systems with
applications to robotics.” Ph.D Thesis, CWRU 1990.
[55] Walsh, G.C. and Sastry, S.S. (1995). On reorienting linked rigid bodies using internal motions.
IEEE Trans. Robotics Automation, 11, 1, 139–145.
Copyright © 2005 by CRC Press LLC

8
D-H Convention
Dr. Jaydev P. Desai
Drexel University
8.1 Introduction
8.2 D-H Parameters
8.3 Algorithm for Determining the Homogenous
Transformation Matrix, A
◦
n
8.4 Examples
8.1 Introduction
Denavit-Hartenberg in 1955 developed a notation for assigning orthonormal coordinate frames to a pair
of adjacent links in an open kinematic chain. The procedure involves finding the link coordinates and
using them to find the 4×4 homogeneous transformation matrix composed of four separate submatricies
to perform transformations from one coordinate frame to its adjacent coordinate frame. D-H notation
is valuable to the area of robotics in which robot manipulators can be modeled as links of rigid bodies.
Most industrial robot manipulators are open loop kinematic chains consisting of a base, joints, links,
and an endeffector. The ability to control a robot endeffector in three-dimensional space requires the
knowledge of a relationship between the robot’s joints and the position and orientation of the endeffector.
The relationship requires the use and an understanding of the rotation matrix and the translation vector.
8.2 D-H Parameters
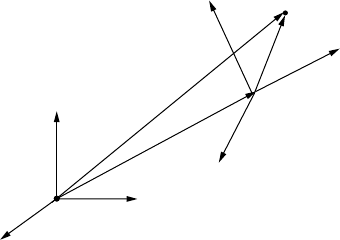
Figure 8.1 shows a schematic of two orthonormal reference frames; one is the fixed (inertial) frame and
the other is the moving (noninertial) frame. The fixed reference frame comprising the triad of unit vectors
(
−→
e
1
,
−→
e
2
,
−→
e
3
) has the origin at point O. The moving frame comprising the triad of unit vectors(
−→
e
1
,
−→
e
2
,
−→
e
3
)
has the origin at point O
. The rotation matrix transforms coordinatesfrom one reference frame to another.
Since most robotic manipulators have individual joint reference frames, which are displaced by a finite
distance and rotation, it is necessary to develop a uniform methodology for deriving the transformation
from one reference frame to the next. The D-H parameters for a robot manipulator help to systematically
derive the transformation from one joint to the next. As a result, it is possible to derive the transformation
from the robot endeffector to the base coordinate frame of the robot arm.
In Figure 8.1(a), a point U in the fixed frame {F} can be described by equation:
−→
U = U
1
−→
e
1
+U
2
−→
e
3
+U
3
−→
e
3
(8.1)
where U
1
, U
2
, and U
3
are the projections of the vector
−→
U along the x, y, and z axes, which have unit
vectors,
−→
e
1
,
−→
e
2
, and
−→
e
3
, respectively. Similarly the same point U can also be described in the moving frame
Copyright © 2005 by CRC Press LLC

8
-2 Robotics and Automation Handbook
Z
{F}
{M}
{F}
U
y′
x′
x
z′
y
O, O′
(a)
z
y
x
{M}
z′
x′
y′
a
(b)
FIGURE 8.1 (a) Schematic of two orthonormal coordinates frames {F} and {M} and (b) rotation by fixed angle
about the x-axis.
{M}, by the equation:
−→
U = U
1
−→
e
1
+U
2
−→
e
2
+U
3
−→
e
3
(8.2)
where U
1
, U
2
, and U
3
are the projections of the vector
−→
U along the x
, y
, and z
axes, which have unit
vectors,
−→
e
1
,
−→
e
2
, and
−→
e
3
, respectively.
From Equation (8.1) and Equation (8.2), we can conclude that
U
1
−→
e
1
+U
2
−→
e
3
+U
3
−→
e
3
= U
1
−→
e
1
+U
2
−→
e
2
+U
3
−→
e
3
(8.3)
By taking the dot product with
−→
e
1
on both sides in Equation (8.3), we get
U
1
= (
−→
e
1
·
−→
e
1
)U
1
+ (
−→
e
2
·
−→
e
1
)U
2
+ (
−→
e
3
·
−→
e
1
)U
3
(8.4)
Similarly taking the dot product with
−→
e
2
, and
−→
e
3
separately in Equation (8.3), we get
U
2
= (
−→
e
1
·
−→
e
2
)U
1
+ (
−→
e
2
·
−→
e
2
)U
2
+ (
−→
e
3
·
−→
e
2
)U
3
(8.5)
U
3
= (
−→
e
1
·
−→
e
3
)U
1
+ (
−→
e
2
·
−→
e
3
)U
2
+ (
−→
e
3
·
−→
e
3
)U
3
(8.6)
From Equation (8.4), Equation (8.5), and Equation (8.6), we conclude that:
U
1
U
2
U
3
=
R
F
M
U
1
U
2
U
3
(8.7)
where R
F
M
is the general expression for rotation matrix transforming coordinates from the moving frame
{M} to the fixed frame {F} and is given by
R
F
M
=
−→
e
1
·
−→
e
1
−→
e
1
·
−→
e
2
−→
e
1
·
−→
e
3
−→
e
2
·
−→
e
1
−→
e
2
·
−→
e
2
−→
e
2
·
−→
e
3
−→
e
3
·
−→
e
1
−→
e
3
·
−→
e
2
−→
e
3
·
−→
e
3
(8.8)
For the specific case of rotation about the x-axis by an angle α, such as that shown in Figure 8.1(b), the
rotation matrix is given by
R
F
M
(x; α) =
10 0
0 e
2
· e
2
e
2
· e
3
0 e
3
· e
2
e
3
· e
3
=
10 0
0 cos(α) −sin(α)
0 sin(α) cos(α )
(8.9)
Copyright © 2005 by CRC Press LLC
D-H Convention 8
-3
O
x
{F}
z
P
F
d
F
y
x′
O′
y′
P
M
z′
U
{M}
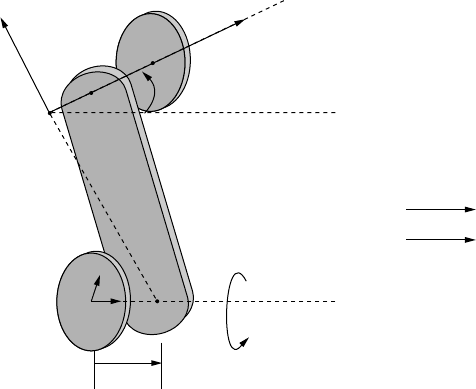
FIGURE 8.2 Schematic of two coordinates frames — one fixed frame {F} and the other moving frame {M} whose
origins are displaced by a finite displacement.
Summarized below are the properties of the rotation matrix:
r
The determinant of the rotation matrix is 1.
r
The norm of any given row or column of the rotation matrix is 1.
r
The dot product of any row or column vector with another row or column vector, (except itself),
is zero.
r
Inverse of the rotation matrix is a rotation matrix, and it is the transpose of the original matrix,
i.e., R
−1
= R
T
.
r
Product of rotation matrices is also a rotation matrix.
Let P
F
be the vector representation in the fixed frame {F} of the point U shown in Figure 8.1(a). The
same point can be expressed by vector p
M
, in the moving frame {M}. Based on Equation (8.7), we can
write
P
F
= R
F
M
p
M
(8.10)
Let us now analyze the second case of two coordinate frames whose origins O and O
are displaced by
a finite displacement vector d
F
(expressed in the fixed frame). As seen from Figure 8.2, the fixed reference
frame {F} has its origin at O while the moving frame {M} has its origin at O
.
Based on previous analysis, if
−→
d
F
=
−→
0 , then we can write P
F
= R
F
M
p
M
. However, since O and O
are
a finite distance apart,
−→
d
F
=
−→
0,wehave
P
F
= R
F
M
p
M
+ d
F
(8.11)
where R
F
M
is the rotation transformation from the moving frame {M} and the fixed frame {F}, and d
F
is the displacement expressed in the fixed frame between the origin O
of the moving frame {M} and the
origin O of the fixed frame {F}.
P
x
P
y
P
z
F
= R
F
M
p
x
p
y
p
z
M
+
d
x
d
y
d
z
F
(8.12)
The rotation matrix and the displacement vector are submatrices of the 4 ×4 homogenous transforma-
tion matrix A
F
M
. Equation (8.12) is the same as Equation (8.11) except that the point P
F
has been written
Copyright © 2005 by CRC Press LLC
8
-4 Robotics and Automation Handbook
X
i
d
i
a
i
O
i
z
i
link i + 1
link i − 1
link i
axis i + 1
axis i
{F
i
}
{F
i−1
}
q
i
a
i
O
i−1
Z
i−1
O′
X
i−1
d
i
= link offset
a
i
= link length
Z
i
a
i
= Z
i−1
about x
i
X
i
q
i
= X
i−1
about z
i−1
FIGURE 8.3 Schematic of the adjacent axes with the appropriately assigned reference frames for determining the
Denavit-Hartenburg parameters.
in vector form. Equation (8.13) provides the expression for the 4 ×4 homogenous transformation matrix
A
F
M
. Thus, we can write
P
x
P
y
P
z
F
=
R
F
M
3×3
d
F
3×1
000
1
p
x
p
y
p
z
⇒A
F
M
=
R
F
M
3×3
d
F
3×1
000
1
(8.13)
Having described the general relationship for transforming coordinates from one reference frame to
the other, we can now discuss the D-H parameters. In Figure 8.3, link i connects link i − 1 to link
i + 1 through a
i
.Thefigure is used to demonstrate the steps involved in determining the Denavit and
Hartenberg parameters. D-H notation is a method of assigning coordinate framesto the different joints of a
robotic manipulator. The method involves determining four parameters to build a complete homogeneous
transformation matrix. These parameters are the twist angle α
i
, link length a
i
, link offset d
i
, and joint
angle θ
i
. Parameters a
i
and α
i
are based on the geometry of the manipulator and are constant values based
on the manipulator geometry, while parameters d
i
and θ
i
can be variable (depending on whether the joint
is prismatic or revolute).
The following steps denote the systematic derivation of the D-H parameters.
1. Label each axis in the manipulator with a number starting from 1 as the base to n as the endeffector.
O
o
is the origin of the base coordinate frame. Every joint must have an axis assigned to it.
2. Set up a coordinateframe for each joint. Startingwith the base joint, set up a right handed coordinate
frame for each joint. For a rotational joint, the axis of rotation for axis i is always along Z
i−1
.Ifthe
joint is a prismatic joint, Z
i−1
should point in the direction of translation.
3. The X
i
axis should always point away from the Z
i−1
axis.
4. Y
i
should be directed such that a right-handed orthonormal coordinate frame is created.
5. For the next joint, if it is not the endeffector frame, steps 2–4 should be repeated.
6. For the endeffector, the Z
n
axis should point in the direction of the endeffector approach.
7. Joint angle θ
i
is the rotation about Z
i−1
to make X
i−1
parallel to X
i
(going from X
i−1
to X
i
).
8. Twist angle α
i
is the rotation about X
i
axis to make Z
i−1
parallel to Z
i
(going from Z
i−1
to Z
i
).
Copyright © 2005 by CRC Press LLC
D-H Convention 8
-5
9. Link length a
i
is the perpendicular distance between axis i and axis i + 1.
10. Link offset d
i
is the offset along the Z
i−1
axis as shown schematically in Figure 8.3. Thus d
i
is the
distance between O
i−1
and O
i
along Z
i−1
(axis i).
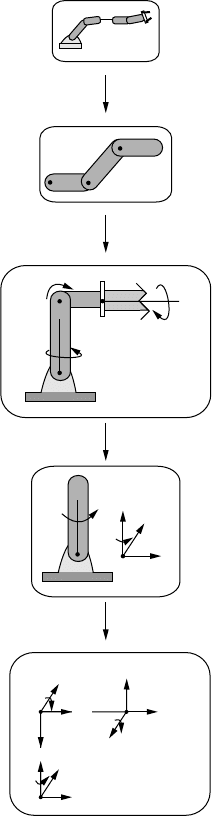
The above steps are shown schematically in the flowchart in Figure 8.4.
In a robot manipulator, there are commonly two types of joints: revolute and prismatic. The revolute
joint allows for rotation between two links about an axis, and the prismatic joint allows for translation
(sliding) motion along an axis. In a revolute joint, the link offset d is a constant while the joint angle θ is
a variable, and in a prismatic joint, the link offset d is variable and the joint angle θ is normally zero. The
link length a
i
and the twist angle α
i
are determined by the geometry of the manipulator and are therefore
constant values.
Locate
Robot arm
Label joints
Determine joint
rotations or translations
q
1
Set up
base coordinate frame
q
q
Z
0
X
0
Y
0
=
O
i−1
O
i+1
O
i
q
2
q
1
q
3
Z
1
q
3
Y
2
Z
2
X
2
Y
1
Y
0
q
1
X
0
q
2
Z
0
X
1
Set up
joint coordinate frames
FIGURE 8.4 Flow chart for the process of determining the Denavit-Hartenburg parameters for a given robot manip-
ulator.(Continued)
Copyright © 2005 by CRC Press LLC
