Kurfess T.R. Robotics and Automation Handbook

Подождите немного. Документ загружается.

The Dynamics of Systems of Interacting Rigid Bodies 7

-11

Thus, if g(t) is a geodesic of the group G, then the equations that describe the rotational motion of a

rigid body are given by

∇

g(t)

g(t) = 0

and these are Euler’s equations for the case that there are no torques applied on the body. Here, ∇ is

the Riemannian connection on the group G, with the Riemannian metric given by the kinetic energy

K =



g

ρ(

g), and ·, ·

as deﬁned above. In the case that there are external torques applied

on the body, we have to modify the equations. We consider the torques T as 1-forms such that T ∈ T

∗

If we denote the kinetic energy metric by ρ : T

G ×T

G → IR, then we can write Euler’s equations in the

form



(∇

g(t)

g(t)) = T

At this point we can further study the rotational dynamics of a rigid body in the case where the body is

constrained to move on a submanifold G



of G. The equations of motion are still going to be geodesics

of the constrained kinetic energy metric. Consider next a submanifold G



of G and let j : G



→ G be

the natural injection. In general, the submanifold G



will not have the property of a subgroup of G.For

example, this would happen if the body was constrained to move in IR

. In this case the subgroup is the

one-dimensional subgroup of plane rotations. The same arguments that occur in the case of Newton’slaw

apply here also. Thus if G



is a submanifold of G, it means that the natural injection is an immersion.

Consequently, the Riemannian metric can be pulled back on the submanifold G



using the natural injection

j. We can write the constrained Euler equations on the submanifold G



in the form



(

∇

g(t)

g(t)) = j

∗

(T)

where



= j

∗

(ρ



◦ j

∗

) and

g(t) = g(t) |



∇ denotes the Riemannian connection on the submanifold



, induced by the Riemannian metric

ρ. Because we are interested in studying the general case of a rigid

body and the result of the presence of certain constraints, we have to consider the Euclidean manifold

× SO(3). In the next example we investigate the representation of Euler’s equations in the form of

geodesics in terms of the coordinates of the group SO(3). This example will illustrate how the arguments

developed up to this point can be applied to this case.

7.5 Example 1: Euler’s Equations for a Rigid Body

Consider a coordinate chart of the Lie group SO(3). We can use as coordinates any convention of the

Euler angles. In this example, we use the Y convention (Goldstein [17]) with φ, θ, ψ as coordinates, where

0 ≤ φ ≤ 2π ,0≤ θ ≤ π,0≤ ψ ≤ 2π . Consider a trajectory g(t) ∈ SO(3) representing the rotational

motion of a rigid body in IR

. The coordinates of the trajectory are given by φ(t), θ (t), ψ(t), and thus the

coordinates of the velocity are

g(t) ={

φ(t),

θ(t),

ψ(t)}. The velocity with respect to the body coordinate

system is ω

= L

−1

∗

g, which when given in matrix form yields



















−sin(θ ) cos(ψ) cos(ψ)0

sin(θ) sin(ψ) cos(ψ)0

cos(θ)01



















The subscript g emphasizes the local character of the metric because the velocities are measured with respect to a

moving coordinate frame.

-12 Robotics and Automation Handbook

With respect to an inertial coordinate frame, the velocity of the body is ω

= R

−1

∗

g, which when given

in matrix form yields



















0 −sin(φ) sin(θ) cos(φ)

0 cos(φ) sin(θ ) sin(φ)

1 0 cos(θ)



















The kinetic energy metric is given by K =



g, 

ω

, ω

. We can choose a coordinate frame

attached to the body such that the three axes are the principle axes of the body; thus,

A =







0 I

00I







We can calculate the quantity A

= L

∗

−1

∗

, which when given in matrix form yields







−sin(θ ) cos(ψ) sin(θ ) sin(ψ) cos(θ)

sin(ψ) cos(ψ)0

001













0 I

00I













−sin(θ ) cos(ψ) sin(ψ)0

sin(θ) sin(ψ) cos(ψ)0

cos(θ)01







We can write Euler’s equations in group coordinates using the formula



(∇

g) = T

The complete system of Euler’s equations, using the coordinates given by the three Euler angles, is given

φ I

sin(ψ)

sin(θ)

+ 2

ψ I

cos(ψ) sin(ψ) sin(θ)

− 2

ψ I

cos(ψ) sin(ψ) sin(θ)

φ I

cos(ψ)

sin(θ)

θ I

sin(ψ)

cos(θ) sin(θ ) +2

θ I

cos(ψ)

cos(θ) sin(θ ) −2

θ I

cos(θ) sin(θ)

−

θ I

sin(ψ)

sin(θ) +

θ I

sin(ψ)

sin(θ) +

θ I

cos(ψ) sin(ψ) sin(θ) −

θ I

cos(ψ) sin(ψ) sin(θ)

θ I

cos(ψ)

sin(θ) −

θ I

cos(ψ)

sin(θ) −

θ I

sin(θ) +

φ I

cos(θ)

cos(ψ) sin(ψ) cos(θ) −

cos(ψ) sin(ψ) cos(θ) +

ψ I

cos(θ) = T

−

sin(ψ)

cos(θ) sin(θ ) −

cos(ψ)

cos(θ) sin(θ ) +

cos(θ) sin(θ ) −

ψ I

sin(ψ)

sin(θ)

ψ I

sin(ψ)

sin(θ) +

φ I

cos(ψ) sin(ψ) sin(θ) −

φ I

cos(ψ) sin(ψ) sin(θ) +

ψ I

cos(ψ)

sin(θ)

−

ψ I

cos(ψ)

sin(θ) +

ψ I

sin(θ) +

θ I

sin(ψ)

− 2

θ I

cos(ψ) sin(ψ)

θ I

cos(ψ) sin(ψ) +

θ I

cos(ψ)

= T

−

cos(ψ) sin(ψ) sin(θ)

θ I

sin(ψ)

sin(θ) −

θ I

sin(ψ)

sin(θ)

−

θ I

cos(ψ)

sin(θ) +

θ I

cos(ψ)

sin(θ) −

θ I

sin(θ) +

φ I

cos(θ) +

cos(ψ) sin(ψ)

−

cos(ψ) sin(ψ) +

ψ I

= T

Observe that the torques T are given in terms of the axes of the Euler angles and, thus, cannot be

measured directly. This happens because the axis of rotation for an Euler angle is moving independent of

the body during the motion. This can be circumvented by using the torques around the principle axes,

and then expressing them via an appropriate transformation to torques measured with respect to the axes

The Dynamics of Systems of Interacting Rigid Bodies 7

-13

of the Euler angles. Because the torques are considered as 1-forms, if we want to translate the torques with

respect to the group coordinates to torques with respect to body coordinates, we have to use a covariant

transformation. The relationship between the corresponding velocities is given by ω

= L

−1

∗

g, and for

the torques we have T

= L

−1

∗

T,whereT

are the torques with respect to the body coordinate system,

and T are the torques with respect to the group coordinate system. Thus, T can be replaced by (L

∗

−1

)

−1

according to the formula



















cos(ψ)

sin(θ)

sin(ψ)

cos(ψ) cos(θ)

sin(θ)

sin(ψ)

sin(θ)

cos(ψ)

−sin(ψ) cos(θ )

sin(θ)

00 1



















Up to this point we have investigated the geometric properties of the basic equations of motion of a

rigid body. Next we will use these properties to model multibody systems where we assume that the rigid

bodies interact through point contact or joints. We have used results from some of our previous work

and techniques from Differential Geometry to study the geometric properties of Newton’s and Euler’s

equations. The ﬁnal goal is to extend the modeling method for dynamical systems introduced by Kron,

which is presented in Hoffmann [20], to interacting mulibody systems.

7.6 The Equations of Motion of a Rigid Body

According to the analysis presented so far, we have derived a representation for the dynamics of a rigid

body which suits our needs. The geodesic representation of the dynamics is the most appropriate to handle

constrained problems. We have described Newton’s and Euler’s equations in their geodesic form on the

manifolds IR

and SO(3), respectively, with the Riemannian kinetic energy metrics



(∇

c(t)

c(t)) = F

(7.3)



(∇

g(t)

g(t)) = T

These metrics can be written in tensor form as E =

and K =

.WhereE and K are

the translational and the rotational kinetic energies, respectively. Also v

, i = 1, 2, 3 are the components

of the velocity

c(t) and u

, i = 1, 2, 3 are the components of the velocity

g(t). Next, we want to combine

the two sets of equations in order to treat them geometrically as a uniﬁed set of dynamical equations for

a rigid body. The conﬁguration manifold where the position and the orientation of the rigid body in the

Euclidean space are described is IE(3) = IR

× SO(3). It is obvious from the analysis so far that we can

use the same process of transforming the translational and rotational dynamics of a rigid body, when the

body is constrained to move on a subset of the conﬁguration space, instead of the total conﬁguration

space. Combining the two sets of dynamics of a rigid body does not affect the geometric properties of

Newton’s and Euler’s equations, as we described them in the previous sections of this chapter. To extend the

reduction process of the dynamics of rigid body motion on the combined conﬁguration manifold IE(3), we

have to introduce a combined kinetic energy metric. More precisely, the sum of the two metrics associated

with the translational and rotational motions is appropriate for a combined kinetic energy metric, i.e.,

E + K =

. We can then deﬁne the equations of motion of a free rigid body.

Definition 7.7 The dynamic equations which deﬁne the motion of a free rigid body are given by the

equations for a geodesic on the manifold IE(3) with Riemannian metric given by the combined metric

 = σ +ρ.

When there are forces and torques acting on the body, then we have to modify the equations of the

geodesics in the form of Equations (7.3). In the case that the body is constrained to move on a subset

M of IE(3), we can describe the dynamics of the body on M under the same conditions we established

in the previous sections for Newton’s and Euler’s equations. Thus, if M is a submanifold of IE(3), then

-14 Robotics and Automation Handbook

we can pull-back the Riemannian metric on M from IE(3) using the natural injection from M to IE(3),

whichisbydeﬁnition an immersion. Actually this is the case that occurs when the rigid bodies interact

through a joint. Depending on the type of joint, we can create a submanifold of IE(3) by considering only

the degrees of freedom allowed by the joint. The other case that we might encounter is when M is a subset

of IE(3), which is also a manifold (with differential structure established independent of the fact that is

a subset ) and there is a map l : M −→ IE(3). This is what happens in the case where the rigid bodies

interact with contact. As we proved in [53], the subset M is also a manifold with a differential structure

established by the fact that M is a submanifold of IE(3) × B. Also we proved in [53] that there exists a map

: M −→ IE(3). In the case that this map is an immersion, we can describe the dynamics of the rigid

body on M.

According to our assumptions about the point interaction between rigid bodies, joints and contact are

the two types of interactions that are being considered. Our intention is to develop a general model for the

dynamics of a set of rigid interacting bodies; therefore, both cases of contact and joint interaction might

appear simultaneously in a system of equations describing the dynamics of each rigid body in the rigid

body system. Thus we will consider the more general case where the dynamics are constrained to a subset

M of IE(3), which is a manifold, and that there exists a map l : M −→ IE(3) which is an immersion. We can

use as before the pull-back l

∗

: T

∗

IE(3) −→ T

∗

M to induce a metric on M. If we denote the Riemannian

metric on IE(3) by  = σ + ρ, then the induced Riemannian metric on M is





= l

∗

 . Consider next a

trajectory on IE(3), r (t):(c(t), g (t)). If this curve is a solution for the dynamics of a rigid body, it satisﬁes

Equations (7.3) which can be written in condensed form





(∇

r (t)

r (t)) = F + T

(7.4)

The term ∇

r (t)

r (t) has the same form as the RHS of the geodesic equations and depends only on the

corresponding Riemannian metric  . When we describe the dynamics on the manifold M, with the

induced Riemannian metric

 , the corresponding curve

r (t) ∈ M should satisfy the following equations:





(

∇

r (t)

r (t)) = l

∗

(F + T)

(7.5)

where F +T is the combined 1-form of the forces and the torques applied to the unconstrained body. The

term

∇

r (t)

r (t) is again the same as the RHS of the equations for a geodesic curve on M and depends only

on the induced Riemannian metric

 . Thus in general, the resulting curve

r (t) ∈ M will not be related

to the solution of the unconstrained dynamics except in the case where M is a submanifold of IE(3), and

in this case we have

r (t) = r (t) |

. It is natural to conclude that the 1-form l

∗

(F + T) includes all forces

and torques that allow the rigid body to move on the constraint manifold M. In the initial conﬁguration

space IE(3), the RHS of the dynamic equations includes all the forces and torques that make the body

move on the subset M of IE(3); these are sometimes referred to as “generalized constraint forces.” Let F

and T

denote, respectively, these forces and torques. We can separate the forces and torques into two

mutually exclusive sets, one set consisting of the forces and torques that constrain the rigid body motion

on M and the other set of the remaining forces and torques which we denote by F

, T

.Thuswehave

F + T = (F

+ T

) ⊕ (F

+ T

). We can deﬁne a priori the generalized constraint forces as those that

satisfy the condition

∗

+ T

) = 0 (7.6)

This is actually what B. Hoffmann described in his work [20] as Kron’s method of subspaces. Indeed in this

work Kron’s ideas about the use of tensor mathematics in circuit analysis are applied to mechanical systems.

As Hoffman writes, Kron himself gave some examples of the application of his method in mechanical

systems in an unpublished manuscript. In this chapter we actually develop a methodology within Kron’s

framework, using the covariant derivative, for the modeling of multibody systems. From the analysis that

we have presented thus far it appears as if this is necessary in order to include not only joints between the

bodies of the system but also point contact interaction.

The Dynamics of Systems of Interacting Rigid Bodies 7

-15

7.7 Constraint Forces and Torques between Interacting Bodies

Because one of the main objectives is to develop dynamic models of multibody systems suitable for control

studies, our ﬁrst task is to investigate some of the ways in which rigid bobies can interact. By interaction

between rigid bodies here we do not mean dynamic interaction in the sense of gravity. Instead, we mean

kinematic interaction through points on the surfaces of the rigid bodies. More precisely, in this work we

say that two rigid bodies are interacting when for a given position of the rigid bodies, the set of points

belonging to the surface of one rigid body coincides with a set of points belonging to the surface of another

rigid body. To put this deﬁnition in a dynamic context, we can say that if γ

(t) and γ

(t) are two curves

in IE(3) describing the motion of two rigid bodies in IR

, then we have interaction if at least two points of

these two curves coincide for some instant of time t = t

. In our construction we restrict the modeling of

interaction by introducing the following assumptions:

1. There is only one point on each body that coincides with one point on the other body at any instant

of time.

2. During the motion of the interacting bodies, there is a nonempty interval of time with positive

measure for which interaction occurs.

3. The interaction points follow continuous paths on the surfaces of the interacting bodies.

The second condition avoids impulsive interaction, which requires special investigation. The third con-

dition is necessary to avoid cases where the interaction might be interrupted for some time and then

continue again. In this later case our model fails unless special care is taken to include such transitions in

the modeling. With these three assumptions for the interaction between rigid bodies, the possible types

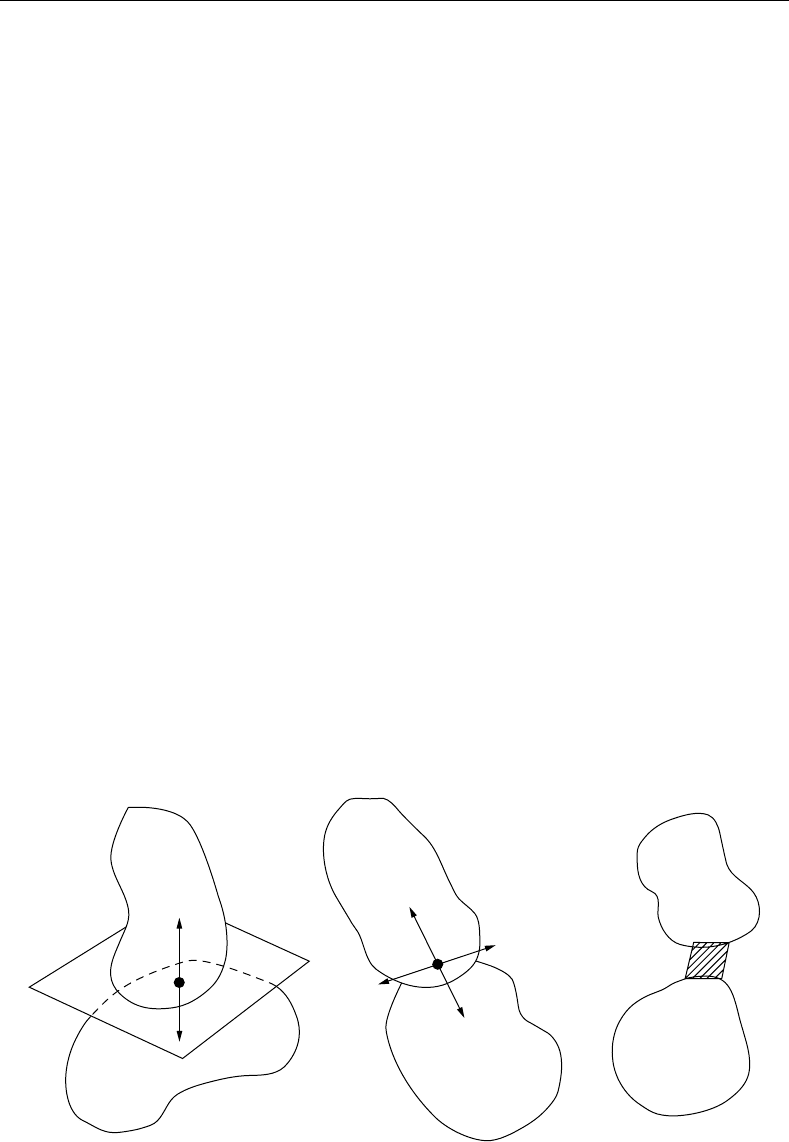
of interaction are illustrated in Figure 7.3.

Precisely the possible interactions include contact, joint connection, and rigid connection. The last case

is of no interest because the two bodies behave dynamically as one. In the other two cases, the interaction

results in a kinematic constraint for one of the bodies. We can replace this constraint in the study of

dynamics with a force acting on each body. In the case of a joint between the interacting bodies, the

constraint can be replaced by forces of equal and opposite signs acting on each body. The direction of

the force is not speciﬁed, see Figure 7.3. In the case of contact, the constraint is replaced by a force in the

direction vertical to the common tangent plane at the point of contact. Forces can act in the tangential

direction, but they have nothing to do with the constraint; they are friction forces. In both cases the forces

are such that the constraints are satisﬁed. This is an a priori consideration for the constraints. In this way,

FIGURE 7.3 Possible types of interaction.

-16 Robotics and Automation Handbook

a constraint resulting from the interaction between two rigid bodies can be replaced by certain forces that

act on the unconstrained bodies. The type of forces depends on the type of constraints. To make this point

more clear, we present several examples.

7.8 Example 2: Double Pendulum in the Plane

In this example we will develop a model for the double pendulum with masses concentrated at the ends

of the links. We regard initially each body separately (Figure 7.4). Thus, the ﬁrst link has one degree of

freedom θ, and the second has three degrees of freedom {φ, x, y}. For the second body (link) x, y are the

coordinates of the center of the mass attached to the end of the link, and φ is the rotational degree of

freedom of the link of the second body. The joint between the two links acts as a constraint imposed on

the second link that is kinematically expressed by

x =l

sin(θ) +l

sin(φ)

y =−l

cos(θ) −l

cos(φ)

Thus, in order that the point at one end of the second link always coincides with the point P of the other

link, a force with components F

, F

is required to act on the unconstrained second link. These forces are

exerted by the tip of the ﬁrst link, and there is an equal but opposite force −F

, −F

acting on the ﬁrst link.

We could have considered the ﬁrst body as a free body in two dimensions constrained by the ﬁrst joint,

but this does not provide any additional insight for the double pendulum problem. We can separate the

rotational and the translational equations of motion for the system consisting of the two bodies in the form



(∇

r (t)

r (t)) = F + T

In our case

ρ =







00 0

0000

00m

000m







–F

(x, y)

FIGURE 7.4 Double pendulum and associated interaction forces.

The Dynamics of Systems of Interacting Rigid Bodies 7

-17

The degrees of freedom of the system are θ, φ, x and y, and the matrix expression for ∇

r (t)

r (t)is













The matrix expression of the 1-form of the forces and the torques F + T is

F + T =







−m

g sin(θ) − F

cos(θ) + F

sin(θ)

−F

cos(φ) + F

sin(φ)

−F

− m







At this point we have described the equations of motion for the two free bodies that make up the system.

Next we proceed with the reduction of the model according to the methodology described above. The

degrees of freedom of the constrained system are

θ,

φ, and we can construct the map ξ according to

ξ : {

θ,

φ}−→{

θ,

φ, l

sin(

θ) +l

sin(

φ), −l

cos(

θ) −l

cos(

φ)}

Next ξ

∗

is calculated:

∗







cos(

θ) l

cos(

φ)

sin(

θ) l

sin(

φ)







It is obvious that the map ξ is an immersion, because the rank(ξ

∗

) = 2. Consequently, we compute

ρ = ξ

∗

ρ:

ρ =



cos(

θ −

φ)

cos(

θ −

φ) l



Applying ξ

∗

on the 1-forms of the forces and the torques on the RHS of the dynamic equations of motion

we obtain

∗

(F + T) =



−m

gsin(

θ) −l

gsin(

θ)

−l

gsin(

φ)



We observe that all the reaction forces have disappeared from the model because we are on the constrained

submanifold. Thus, we could have neglected them in the initial free body modeling scheme. We continue

with the calculation of

∇

r (t)

r (t), which deﬁnes a geodesic on the constraint manifold. The general form

of the geodesic is [12,14]

+ 

-18 Robotics and Automation Handbook

where x

are the degrees of freedom of the constrained manifold and 

are the Christoffel symbols. We

have that



= 0



= 0



cos(

θ −

φ) sin(

θ −

φ)

−l

cos(

θ −

φ)



) sin(

θ −

φ)

−l

cos(

θ −

φ)



sin(

θ −

φ)

−l

cos(

θ −

φ)



cos(

θ −

φ) sin(

θ −

φ)

−l

cos(

θ −

φ)

+ 



θ +2

+ 2

φ + 2

+ 2



We apply



in the form of a matrix operating on

∇

r (t)

r (t), and equating the result with ξ

∗

(F + T) yields

the following equations of motion:



+ m

θ +m

cos(

θ −

φ)

φ +l

sin(

θ −φ)

φ + m

cos(

θ −

φ)

θ −m

sin(

θ −

φ)





−m

sin(

θ) − m

sin(

θ)

sin(

φ)



which are exactly the equations that are obtained using the classical Lagrangian formulation [41].

7.9 Including Forces from Friction and from

Nonholonomic Constraints

Friction forces,and the resulting torques, can be added naturally within the modeling formalism presented.

Frictional forces are introduced when a body moves in contact with a nonideal surface and the friction

forces have a direction which opposes the motion. There is a signiﬁcant literature on the subject of friction,

which actually constitutes the separate scientiﬁc ﬁeld of triboblogy. What is important for our formulation

is that the direction of the friction forces is opposite to the direction of the motion. Modeling of the friction

forces is also a complicated subject and depends on additional information about the nature of contacting

surfaces. The magnitude of the friction forces can depend on the velocity or the square power of the

velocity [3], for example. At this point we will not investigate the inclusion of friction forces and torques as

functions of the velocities and other parameters. Because a complete model requires this information, we

will leave this matter for future investigation. Nonholonomic constraints are a special case of constraints

that appear in a certain class of problems in dynamics. These constraints are not integrable (e.g., rolling)

and can be represented as 1-forms. Integrability is a property deﬁned for a set of equations describing

kinematic constraints with the general form J (q)dq = 0 (1-forms), where J (q)isn × (n − m) matrix

with rank equal to (n − m). If the initial dynamic system can be described on a n-dimensional manifold

M, then the constraint equation J (q)dq = 0 is said to be integrable on M if there exists a smooth (n −m)-

dimensional foliation whose leaves are (n −m)-dimensional submanifolds with all of their points tangent

to the planes deﬁned by the constraint equations [4]. Alternatively, integrability of the constraints can be

deﬁned with respect to the associated vector ﬁelds, vanishing when the 1-forms of constraints operate on

them. In this context integrability of the vanishing vector ﬁelds is deﬁned by the Frobenious theorem [12].

The Dynamics of Systems of Interacting Rigid Bodies 7

-19

From the existing literature it is obvious that these types of constraints are more difﬁcult to deal with

and a lot of attention is required in their use. Many times they lead to falacies [41] and they have been

the cause of many discussions. It has also been shown that using the nonholonomic constraints with

different variational principles (D’ Alembert, Hamilton, etc.) can lead to different solutions (Vakonomic

mechanics [22–25]). In our formalism we deal with elementary (not generalized) entities like forces and

torques applied on each body. Initially it appears as if there is no better way to introduce a force or a

torque from a nonholonomic constraint in any modeling formalism. The forces and the torques from a

nonholonomic constraint are frictional, but they produce no work. The virtual work produced by these

forces and torques is of third order (δx

) in the related displacement [18], and these forces and torques

are acting on the body to keep the constraint valid. This is equivalent to requiring that the forces and the

torques act in the direction of the 1-form representing the nonholonomic constraint (Burke [14]). This

interpretation allows the introduction of Lagrange multipliers in a nonvariational framework, and a force

or torque in the direction of the 1-form ω should be of the form F = λω.

Next, consider a procedure where the objective is to model the dynamics of a set of interacting bodies.

We begin by considering each body separately and all the forces and torques that are acting on the body,

including applied and reaction forces and torques. Then, because of the existence of constraints, each body

is actually moving on a submanifold of the original conﬁguration space deﬁned by a natural injection j .

The resulting forces and torquesare, as we pointed out earlier, l

∗

(F +T). The constraint forces and torques

disappear from the dynamics on the resulting submanifold because l

∗

) = 0. Thus, in considering

the dynamics on the submanifold, we should not include the torques and forces that result because of the

constraints at the initial stage of the modeling. What is important, though, is being able to distinguish

between constraint forces and torques and the other exerted forces and torques caused from friction, for

example. These other exerted forces and torques do have an effect on the dynamics on the submanifold. In

the case of contact between two bodies for example, friction forces can be introduced in the direction of

the common tangent plane. In the reduction process of the initial conﬁguration space, this friction force

will remain present. The effect of these types of forces can dramatically alter the behavior of a rigid body,

producing interesting phenomena; for example, in the case of contact interaction, they can cause rolling

phenomenon. To control a system using a model that includes these types of forces and torques, we need to

introduce them as measurable quantities in the model. Certain assumptions can be used a priori for special

cases, like pure sliding motion. However, there are other situations where the cause of a change from one

type of motion to another, with little or no a priori information about the frictional forces and torques,

is unknown. Neglecting information on how the forces and torques can affect the qualitative properties

of the motion can be disastrous from a modeling perspective. On the other hand, trying to describe the

dynamics using principles like the D’Alembert-Lagrange or Hamiltonian formulations can result in an

ambiguous model, as in the case of nonholonomic constraints, see, for example [4,22–25]. Next we present

a systematic procedure for modelling the dynamics of a set of interacting bodies using the conﬁguration

space reduction method. This is done in the context of the above discussion, regarding the forces and the

torques that are involved as a result of the interaction. Several examples are used to illustrate the approach.

7.10 Example 3: The Dynamics of the Interaction

of a Disk and a Link

The constrained conﬁguration space of the disk is M

, a two-dimensional submanifold of IE(3) × B

.Let

denote the surface of the disk and let B

denote the surface of the link. The coordinates of IE(2) × B

are {z

, z

, θ, φ}, and for the submanifold they are {

θ}. In a similar way the constrained conﬁguration

space of the link is M

, a two-dimensional submanifold of IE(2) × B

. The coordinates of M

are {

}

and for IE(2) × B

they are {y

, y

, θ

, τ

The modeling methodology requires deriving Newton’s and Euler’s equations for each body separately,

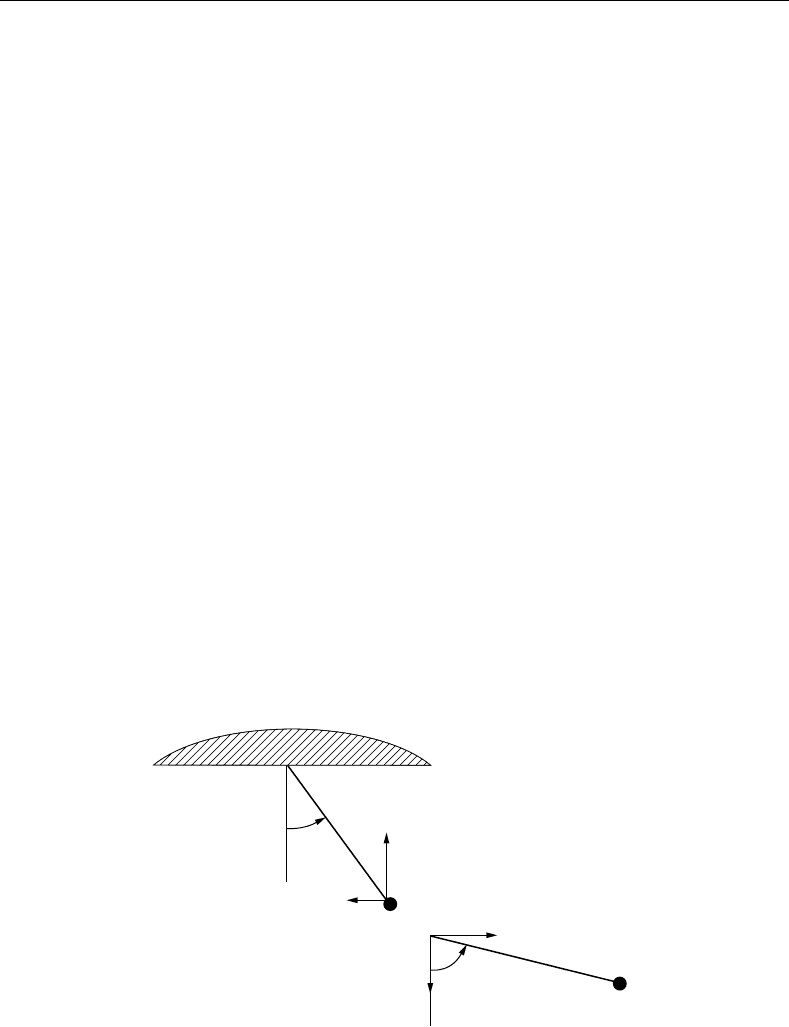
with the external and the reaction forces and torques included as shown in Figure 7.5. At this point, we

-20 Robotics and Automation Handbook

, y

)

, z

)

–v



FIGURE 7.5 Disk in contact with a link.

assume that there are no friction forces generated by the contact. The set of the dynamic equations is

=−vsin(θ

)

= u − vcos(θ

) −mg

θ =0

= vsin(θ

)

= vcos(θ

) −m

= u

− vτ

Where m, I are the mass and the moment of inertia of the disk, m

, I

are the mass and the moment

of inertia of the link, and u

is the input (applied) torque. As we mentioned previously, the dynamic

equations that describe the motion for each body are described initially on IE(2). The torques and the

forces are 1-forms in T

∗

IE(2). The dynamic equations of the combined system are deﬁned on IE(2) ×IE(2),

but the constrained system actually evolves on M

× M

. We can restrict the original system of dynamic

equations to M

× M

using the projection method developed earlier. Thus we need to construct the

projection function ξ : M

× M

−→ IE(2) × IE(2). We already have a description of the projection

mappings for each constrained submanifold, µ

: M

−→ IE(2) and ν

: M

−→ IE(2). We can use

the combined projection function ξ = (µ

, ν

) for the projection method. As stated previously, the

forces and torques are 1-forms in T

∗

IE(2), and for the link, for example, they should have the form

a(y

, y

, θ

)dy

+b(y

, y

, θ

)dy

+c(y

, y

, θ

)dθ

. However, in the equations for the 1-forms we have the

variables τ

and u

, which are different from {y

, y

, θ

}. The variable u

is the input (torque) to the link,

and τ

is the point of interaction between the link and the disk. Thus τ

can be viewed as another input

to the link system. In other words, when we have contact between objects, the surfaces of the objects in

contact must be included in the input space. When we project the dynamics on the constraint submanifold

, then τ

is assigned a special value because in M

, τ

is a function of {

} (the coordinates of M

We can compute the quantities ξ

∗

and ξ

∗

that are needed for the modeling process. The projection map ξ

is deﬁned as

ξ : {

θ,

}−→



,1,

θ,

1 +sin(θ

)(

−

)

cos(

)

+ 1,

