Kurfess T.R. Robotics and Automation Handbook

Подождите немного. Документ загружается.

Trajectory Planning for Flexible Robots 9

-15

Desired Response

FIGURE 9.20 Response to shaped square trajectory.

constructing reaction jet commands, the amount of fuel can be limited or set to a speciﬁc amount [39–44].

It is also possible to limit the transient deﬂection [45, 46]. Furthermore, vibration reduction and slewing

can be completed simultaneously with momentum dumping operations [47].

The sections above are not intended to be complete, but they are an attempt to give an introduction to

and a reference for using command generation in the area of trajectory following. The list of successful

applications and extensions of command generation will undoubtedly increase substantially in the years

to come.

9.3 Feedforward Control Action

Feedforward control is concerned with directly generating a control action (force, torque, voltage, etc.),

rather than generating a reference command. By including an anticipatory corrective action before an

error shows up in the response, a feedforward controller can provide much better trajectory tracking than

with feedback control alone. It can be used for a variety of cases such as systems with time delays, nonlinear

friction [48], or systems performing repeated motions [49]. Most feedforward control methods require

an accurate system model, so robustness is an important issue to consider. Feedforward control can also

be used to compensate for a disturbance if the disturbance itself can be measured before the effect of the

disturbance shows up in the system response. A block diagram for such a case is shown in Figure 9.21.

The generic control system diagram that was ﬁrst shown in Figure 9.5 shows the feedforward block

injecting control effort directly into the plant, as an auxiliary to the effort of the feedback controller.

Decoupling this type of control from the action of the command generator, which creates an appropri-

ate reference command, makes analysis and design of the overall control system simpler. However, this

nomenclature is not universal. There are numerous papers and books that refer to command generation

Plant

Feedback

Controller

ΣΣ

Feedforward

Controller

Disturbance

Measurement

FIGURE 9.21 Feedforward compensation of disturbances.

-16 Robotics and Automation Handbook

+ bs

Feedforward

Controller

-sτ

FIGURE 9.22 Feedforward compensation of a system with a time delay.

as feedforward control. In order to establish clarity between these two fundamentally different control

techniques, the following nomenclature will be used here:

Command Generation attempts to produce an appropriate command signal to a system. The

system could be open or closed loop. In an open loop system, the command would be a force

acting directly on the plant. In a closed-loop system, the command would be a reference signal

to the feedback controller.

Feedforward Control produces a force acting directly on the plant that is auxiliary to the feedback

control force. Without a feedback control loop, there cannot be feedforward control action.

One reason for the inconsistent use of the term feedforward is because some techniques can be employed in

either a feedforward manner or in the role of a command generator. However, the strengths and weakness

of the techniques change when their role changes, so this effect should be noted in the nomenclature.

9.3.1 Feedforward Control of a Simple System with Time Delay

To demonstrate a very simple feedforward control scheme, consider a system under proportional feedback

control that can be modeled as a mass-damper system with a time delay. The block diagram for this case

is shown in Figure 9.22. The desired output is represented by the reference signal R. The actions of the

feedforward control and the feedback control combine to produce the actuator effort U that then produces

the actual output Y.

Let us ﬁrst examine the response of the system without feedforward compensation. Suppose that the

feedback control system is running at 10 Hz, the time delay is 0.1 sec, m = 1, and b = 0.5. The dynamic

response of the system can be adjusted to some degree by varying the proportional gain K . Figure 9.23

shows the oscillatory step response to a variety of K values. This is a case where the system ﬂexibility results

from the feedback control rather than from the physical plant. Note that for low values of K , the system is

−0.5

0.5

1.5

2.5

246810

K = 1 K = 3 K = 7

Response

Time

FIGURE 9.23 Step response of time-delay system without feedforward compensation.

Trajectory Planning for Flexible Robots 9

-17

−20

−15

−10

−5

0246810

K = 1 K = 3 K = 7

Control Effort

Time

FIGURE 9.24 Control effort without feedforward compensation.

sluggish. The system rise time can be improved by increasing K , but that strategy soon drives the system

unstable. The corresponding control effort is shown in Figure 9.24.

Rather than performing a step motion, suppose the desired motion was a smooth trajectory function

such as:

r (t) = 1 −cos(ωt)

(9.23)

The simple proportional feedback controller might be able to provide adequate tracking if the frequency

ofthe desiredtrajectorywas verylow. However, if the trajectory is demanding (relativetosystemfrequency),

then the feedback controller will provide poor tracking as shown in Figure 9.25. To improve performance,

we have several options ranging from redesigning the physical system to improve the dynamics and reduce

the time delay, adding additional sensors, improving the feedback controller, using command shaping, or

adding feedforward compensation. Given the system delay, feedforward compensation is a natural choice.

A simple feedforward control strategy would place the inverse of the plant in the feedforward block

shown in Figure 9.22. If this controller can be implemented, then the overall transfer function from

desired response to system response would be unity. That is, the plant would respond exactly in the desired

manner. There are, or course, limitations to what can be requested of the system. But, let us proceed with

this example and discuss the limitations after the basic concept is demonstrated. In this case, the plant

0246810

K = 1

K = 3

K = 7

Desired Path

Response

Time

FIGURE 9.25 Tracking a smooth function without feedforward compensation.

-18 Robotics and Automation Handbook

−0.5

0.5

1.5

2.5

0246810

Desired Path

K = 1

K = 7

Response

Time

FIGURE 9.26 Tracking a smooth function with feedforward compensation.

transfer function including the time delay is

−sτ

+ bs

(9.24)

The feedforward controller would then be

+ bs

−sτ

(9.25)

Note that this would be implemented in the digital domain, so the time delay in the denominator

becomes a time shift in the numerator. This time shift would be accomplished by essentially looking ahead

at the desired trajectory. Without knowing the future desired trajectory for at least the amount of time

corresponding to the delay, this process cannot be implemented.

Figure 9.26 shows that under feedforward compensation, the system perfectly tracks the desired trajec-

tory for various values of the feedback gain. This perfect result will not apply to real systems because there

will always be modeling errors. Figure 9.27 shows the responses when there is a 5% error in the system mass

and damping parameters. With a low proportional gain, the tracking is still fairly good, but the system

goes unstable for the higher gain. If the error is increased to 10%, then the tracking performance with the

low gain controller also starts to degrade as shown in Figure 9.28.

One important issue to always consider with feedforward control is the resulting control effort. Given

that the feedback controller generates some effort and the feedforward adds to this effort, the result might

−0.5

0.5

1.5

2.5

0246810

Desired Path K = 1 K = 7

Response

Time

FIGURE 9.27 Effect of 5% model errors on feedforward compensation.

Trajectory Planning for Flexible Robots 9

-19

−0.5

0.5

1.5

2.5

0246810

Desired Path K = 1

Response

Time

FIGURE 9.28 Effect of 10% model errors on feedforward compensation.

be unrealistically high effort that saturates the actuators. Furthermore, the control effort can be highly

dependent on the desired trajectory. Consider again the smooth trajectory given in Equation (9.23). The

Laplace transform is

R(s ) =

s(s

+ ω

)

(9.26)

Sending the desired trajectory through the feedforward compensator, results in a feedforward control

effort of

(s)R(s ) = e

sτ

(ms + b)

+ ω

(9.27)

Converting this into the time domain yields

mω

cos(ω[t + τ ]) +bωsin(ω[t + τ ]) (9.28)

sin(ω[t + τ ] + C

) (9.29)

where

= ω



+ b and C

= tan

−1



mω



(9.30)

Note that the control effort increases with the desired frequency of response. Therefore, requesting very

fast response will lead to a large control effort that will saturate the actuators. This effect is demonstrated

in Figure 9.29. Finally, if the desired trajectory has discontinuous derivatives that cannot physically be

realized, such as step and ramp commands for systems that have an inertia, then the feedforward control

effort would also be unrealizable and saturate the actuators.

9.3.2 Feedforward Control of a System with Nonlinear Friction

The above example showed the possibility of using feedforward compensation to deal with a time delay

and ﬂexibility induced by the feedback controller. Another good use of feedforward control is to help

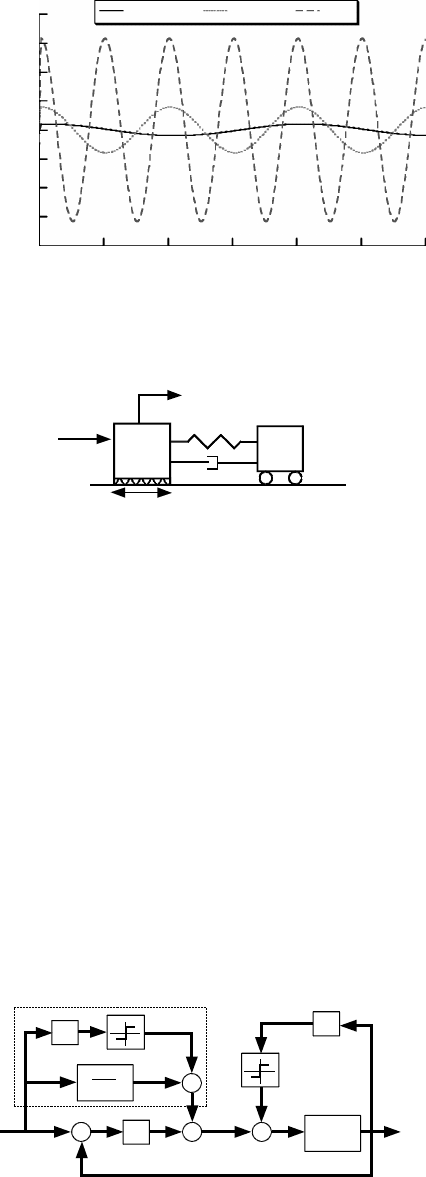
compensate for nonlinear friction. Consider the system shown in Figure 9.30. An applied force moves a

mass subject to Coulomb friction. Attached to the base unit is a ﬂexible appendage modeled as a mass-

spring-damper system.

-20 Robotics and Automation Handbook

−200

−150

−100

−50

100

150

200

0 0.5 1 1.5 2 2.5 3

0.5 Hz 1 Hz

2 Hz

Control Effort

Time

FIGURE 9.29 Control effort tracking various frequencies with feedforward compensation.

applied

friction

FIGURE 9.30 Model of system with Coulomb friction.

If a reasonable model of the friction dynamics exists, then a feedforward compensator could be useful

to improve trajectory tracking. A block diagram of such a control system is shown in Figure 9.31. Note

again that the feedforward compensator contains an inverse of the plant dynamics.

Let us ﬁrst examine the performance of the system without the feedforward compensation. To do this,

we start with a baseline system where Mass A is 1, Mass B is 0.5, the spring constant is 15, the damping

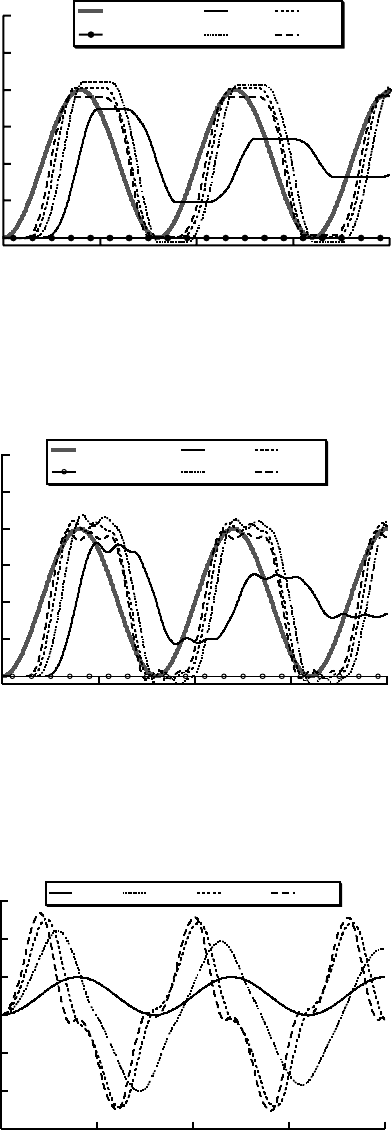
constant is 0.3, and the coefﬁcient of friction is 0.3. Figure 9.32 shows the response of Mass A for various

values of the feedback control gain when the desired path is a cosine function in Equation (9.23). For a gain

of 1, the control effort is too small to overcome the friction, so the system does not move. Larger values

of gain are able to break the system free, but the trajectory following is very poor. Figure 9.33 shows the

response of Mass B for the same range of feedback gains. This part of the system responds with additional

ﬂexible dynamics. The corresponding control effort is shown in Figure 9.34.

When the feedforward compensator is turned on, the tracking improves greatly, as shown in Figure 9.35.

The control effort necessary to achieve this trajectory following is shown in Figure 9.36. The control effort

Feedforward Controller

Friction

applied

Σ Σ

−

FIGURE 9.31 Block diagram of friction system with feedforward compensation.

Trajectory Planning for Flexible Robots 9

-21

0.5

1.5

2.5

0 5 10 15 20

Desired Path

K = 1

K = 3

K = 5

K = 7

K = 9

Response of Mass A

Time

FIGURE 9.32 Response of mass A in friction system without feedforward compensation.

0.5

1.5

2.5

0 5 10 15 20

Desired Path

K = 1

K = 3

K = 5

K = 7

K = 9

Response of Mass B

Time

FIGURE 9.33 Response of mass B in friction system without feedforward compensation.

−6

−4

−2

0 5 10 15 20

K = 1 K = 3 K = 5 K = 7

Control Effort

Time

FIGURE 9.34 Control effort in friction system without feedforward compensation.

-22 Robotics and Automation Handbook

0.5

1.5

2.5

0 5 10 15 20

Desired Path

, K = 3

, K = 7

Response

Time

FIGURE 9.35 Response of friction system with feedforward compensation.

contains discontinuous jumps that will not be strictly realizable with real actuators, so the actual trajectory

tracking will not be perfect, as predicted through simulation. As with any feedforward control technique,

robustness to modeling errors is an issue. Figure 9.37 shows how the tracking degrades as modeling errors

are introduced. Recall that feedforward control is dependent not only on the system model but also on the

desired trajectory. This is apparent in Figure 9.38 which shows the same modeling errors cause considerably

more tracking problems when the period of the desired trajectory is changed from 8 sec, as in Figure 9.37,

to 10 sec.

9.3.3 Zero Phase Error Tracking Control

The above feedforward control scheme is subject to the same limitations as for the system with a time

delay. For example, only physically realizable desired trajectories can be utilized. Another important

limitation exists with model-inverting feedforward control schemes. If the model contains non-minimum

phases zeros, then the model cannot be inverted. This would require implementing unstable poles in the

feedforward control path. A way around this problem is to invert only the portion of the plant that yields

a stable feedforward path.

To improve the performance of such partial-plant-inversion schemes, various extensions and scaling

techniqueshavebeendeveloped. A goodexampleof afeedforward controllerthat only invertstheacceptable

parts of the plant is the zero phase error tracking controller (ZPETC) [50]. In the digital formulation of

−4

−2

0 5 10 15 20

Desired Path

Control Effort

Amplitude

Time

FIGURE 9.36 Control effort for friction system with feedforward compensation.

Trajectory Planning for Flexible Robots 9

-23

0.5

1.5

0 5 10 15 20

Desired

5% Error

10% Error

15% Error

20% Error

Response

Time

FIGURE 9.37 Response of mass B with modeling errors.

this controller, the plant transfer function is written in the following form:

G(z

−1

) =

−d

−1

)

A(z

−1

)

(9.31)

The numerator is broken down into three parts — a pure time delay z

−d

, a part that is acceptable for

inversion B

, and a part that should not be inverted B

9.3.4 Conversion of Feedforward Control to Command Shaping

Consider the control structure using a ZPETC controller shown in Figure 9.39. The physical plant and the

feedback controller have been reduced to a single transfer function described by

−1

) =

−d

−1

)

−1

)

(9.32)

where B

−1

) = b

+ b

−1

+···+b

−s

.Thec subscripts have been added to denote the transfer

function now represents the entire closed-loop system dynamics. The superscripts on the numerator again

refer to parts that are acceptable and unacceptable for inversion. In this case, the output of the ZPETC is

a reference signal for the closed-loop controller. It does not directly apply a force to the plant. It therefore

0.5

1.5

0 5 10 15 20 25

Desired Path

5% Error

10% Error

15% Error

20% Error

Response

Time

FIGURE 9.38 Response of mass B with modeling errors and slower tr-ajectory.

-24 Robotics and Automation Handbook

−1

)

ZPETC

FIGURE 9.39 ZPETC as a command generator.

does not try to overrule or add to the efforts of the feedback controller. Given this structure, the ZPETC

should be considered a command generator, rather than a feedforward compensator.

To cancel the acceptable portion of the plant model, create the ZPETC so that the reference signal is

given by

r (k) =

−1

)

−1

(1)

∗

(k + d)

(9.33)

Rather than invert the unacceptable zeros, the reference signal is formed using the unacceptable portion

evaluated at 1. B

(1) is a scaling term to compensate for the portion of the system that is not inverted. Note

that the ZPETC operates on a term related to the desired trajectory denoted by y

∗

. Choosing this function

carefully can also help compensate for the incomplete model inversion. Note that for perfect trajectory

tracking, we would choose

∗

(k) =

(1)

−1

)

(k) (9.34)

However, the term in the denominator would cause unacceptable oscillation or instability in the calculation

of y

∗

. The natural choice would then be to simply choose

∗

(k) = y

(k) (9.35)

However, this would lead to a phase lag between the desired response and the actual response. In order to

reduce the phase lag, the ZPETC uses

∗

(k) =

(z)

(1)

(k) (9.36)

The total effect of the ZPETC can then be summarized as

r (k) =

−1

u∗

−1

)

−1

)



(1)



(k + d + s ) (9.37)

where s is the number of unacceptable zeros and B

u∗

−1

) = b

+ b

c(s−1)

−1

+···+b

−s

9.4 Summary

Trajectory following with ﬂexible robotic systems presents many challenges. For these applications, it is

obviously very important to design good mechanical hardware and a good feedback controller. Further-

more, a baseline command trajectory must be generated using knowledge of the physical limitations of the

system. Once that is accomplished, the detrimental effects of the system ﬂexibility on trajectory following

can be reduced through use of command shaping and feedforward control.

Command shaping operates by taking the baseline command and changing its shape slightly so that it

will not excite the ﬂexible modes in the system. Given that this process changes the shape of the reference

command, there is the possibility that the system will not exactly follow the intended trajectory. However,

the minor deviations produced by command shaping are usually less than the trajectory deviations caused

by the deﬂection that would occur without command shaping. Many command shaping methods have

good robustness to modeling errors. Therefore, they can be used on a wide variety of systems, even if their

dynamics are somewhat uncertain or change over time.