Куренков В.Ф. Химия высокомолекулярных соединений: Конспект лекций
Подождите немного. Документ загружается.

41
сополимеризации (рис. 8). Как видно из рис. 8, форма кривых
состава зависит от значений констант сополимеризации. Рас-
смотрим различные случаи:
1)
r
1
> 1 и r
2
< 1 , т.е. для всех соотношений концентраций
мономеров в исходной смеси сополимер обогащен звеньями М
1
;
2)
r
2
> 1 и r
1
< 1, т.е. при всех соотношениях концентраций
мономеров в исходной смеси сополимер обогащен звеньями М
2
;
3)
r
1
< 1 и r
2
< 1, т.е. при малых содержаниях М
1
в исходной
мономерной смеси сополимер обогащен звеньями М
1
, а при
больших – звеньями М
2
. В этом случае наблюдается склонность
к чередованию с сополимере звеньев М
1
и М
2
, которая усилива-
ется при приближении к нулю значений r
1
и r
2
. Кривая состава
пересекает диагональ диаграммы составов в точке, называемой
азеотропной, когда состав сополимера равен составу мономер-
ной смеси.
4)
r
1
> 1 и r
2
> 1 - редко реализуемый на практике случай,
когда должна получаться смесь гомополимеров или образовы-
ваться сополимер с длинными последовательностями одинако-
вых звеньев.
5)
r
1
= r
2
= 1 , т.е. для всех исходных соотношений концен-
траций мономеров состав сополимера равен составу мономерной
смеси. В этом случае обеспечивается получение однородного со-
полимера вплоть до полного исчерпания мономеров.
6)
r
1
≈ r
2
≈ 1. При этом независимо от состава смеси моно-
меров образуется эквимолекулярный сополимер с регулярным
чередованием звеньев.
Обычно произведение r
1
r
2
< 1 и реже r
1
r
2
= 1, что отвечает
идеальной сополимеризации.
Следует отметить, что дифференциальное уравнение сополи-
меризации применимо только при составах сополимера, опреде-
ленных при малых конверсиях. Если сополимер получен при
большой глубине превращения, то для расчёта используется ин-
тегральное уравнение Майо-Льюиса или Абкина. Указанные

42
уравнения основаны на допущении о независимости реакцион-
ной способности растущих частиц от природы предпоследнего
звена. Уравнения сополимеризации неприменимы при зависимо-
сти реакционной способности реагирующих частиц от природы
предпоследнего звена, в случае сополимеризации мономеров с
полярными и объёмными заместителями, в случае параллельно
протекающей с сополимеризацией деполимеризации, в случае
гетерофазной сополимеризации и др.
Определение констант сополимеризации
.
Определение констант сополимеризации осуществляют раз-
личными методами, но все они заключаются в эксперименталь-
ном определении состава сополимера, полученного при малых
конверсиях (менее 5%) для нескольких различных смесей моно-
меров М
1
и М
2
. Введём обозначение для состава исходной моно-
мерной смеси и состава сополимера:
E = [М
1
]/[ М
2
] и Z = [m
1
]/[ m
2
]
Метод Майо-Льюиса
Уравнение сополимеризации можно записать в следующем
виде:
r
2
= r
1
(E
2
/ Z) + (
Z
E
– E) (23)
Затем для произвольных значений r
1
рассчитывают пo урав-
нению (23) соответствующие значения r
2
и для каждой пары зна-
чений E и Z получают серию прямых в координатах r
2
= f(r
1
)
(рис.9). По координатам точки пересечения прямых находят ис-
комые значения r
2
и r
1
.

43
Рис. 9. Графический способ определения констант
сополимеризации по методу Майо-Льюиса.
Метод Файнемана-Росса
В основе метода лежит модификация уравнения сополиме-
ризации
E –
Z
E
= – r
2
+ r
1
(Е
2
/ Z) (24)
При построении зависимости E–
Z
E
от (Е
2
/Z) получают пря-
мую (рис. 10) и по величине отрезка, отсекаемого на оси орди-
нат, определяют значение (–r
2
), а по углу наклона прямой к оси
абсцисс –r
1
(r
1
= tg α).
Рис. 10. Графический спо-
соб определения констант
сополимеризации по мето-
ду Файнемана-Росса.
Здесь х = (E
2
/ Z) ,
у = E –
Z
E
.
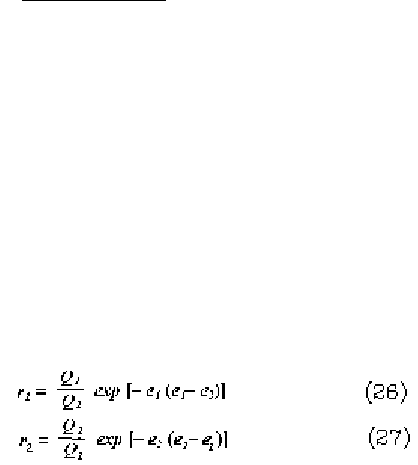
44
Схема “Q – e”
Для количественной характеристики реакционной способно-
сти мономеров в радикальной сополимеризации большое рас-
пространение получила схема “Q – e”, предложенная Алфреем и
Прайсом. В основе метода лежит допущение, что константу ско-
рости присоединения радикала i к мономеру j можно предста-
вить уравнением:
k
ij
= D
i
Q
j
exp (– e
i
e
j
) (25)
Индексы i и j относятся к макрорадикалу и мономеру соот-
ветственно. В уравнении (25) D и Q – параметры, характеризую-
щие общую реакционную способность радикала и мономера; e –
параметр, характеризующий полярные свойства (мономеру и ра-
дикалу приписывается одно и то же значение e).
Значения констант сополимеризации связаны с параметрами
Q и e уравнениями:
Значения Q
1
и e
1
вычисляют из опытных значений r
1
и r
2
при использовании в качестве стандарта мономера стирола. Вы-
бор стирола обусловлен тем, что он способен сополимеризовать-
ся с большинством мономеров. Для стирола Q
2
=1 и e
2
= – 0,8.
Согласно схеме Q – e мономеры с резко отличающимися пара-
метрами e характеризуются тенденцией к чередованию звеньев в
цепи. Сополимеризация мономеров с близкими параметрами Q и
почти идентичными параметрами e приводит к азеотропной со-
полимеризации.
Схема Q – e имеет приближенный и эмпирический характер,
а также не имеет полного теоретического обоснования. Однако
схема Q – e полезна, поскольку на её основе можно оценить от-
носительную реакционную способность мономеров и роль по-
лярны факторов для большинства сополимеризующихся моно-
меров. Значения Q и e для многих мономеров приводятся в спра-
вочной литературе.

45
Состав сополимера при глубоких конверсиях. Уравнение со-
полимеризации (для данной пары мономеров с известными кон-
стантами сополимеризации и определенным составом исходной
мономерной смеси) позволяет рассчитать мгновенный состав со-
полимера. Исходя из уравнения сополимеризации нельзя пред-
сказать состав сополимера, поученного при конверсиях 50-60%,
что имеет место в промышленных процессах. Это следствие из-
менения состава непрореагировавших мономеров с конверсией.
Изменение с конверсией состава мономерной смеси и состава
сополимера приводит к прогрессирующей композиционной неод-
нородности образующегося сополимера. Распределение по со-
ставу (степень неоднородности) зависит от конверсии. С повы-
шением конверсии увеличивается неоднородность сополимера
по составу.
Для получения однородного по составу сополимера нужно
руководствоваться следующим:
• подбирают мономерные пары с константами сополимери-
зации, близкими единице, чтобы состав мономерной смеси ми-
нимально изменялся с увеличением конверсии;
• реакцию проводят по возможности ближе азеотропного
состава;
• ограничиваются минимально возможными конверсиями
при получении сополимеров;
• сохраняют постоянным состав мономерной смеси путём
добавления в ходе реакции в реакционную смесь более активно-
го сомономера.
2.1.3. Ионная полимеризация
В промышленности до середины 50-х годов ХХ века при по-
лучении полимеров основное место занимали радикальные про-
цессы. В настоящее время наряду с радикальными используются
и ионные процессы, на долю которых приходится около 20% от

46
общей массы полимеризационных материалов. Ионной полиме-
ризацией в промышленности получают ПЭ, ПП, ПБ, полифор-
мальдегид.
Ионная полимеризация вызывается различными полярными
соединениями, которые приводят к разрыву ненасыщенных свя-
зей (С=С, С=О, С≡N) или раскрытию карбоциклов и циклов, со-
держащих гетероатомы (О, N, S). Кроме того, ионная полимери-
зация может протекать и под действием ионизирующего излуче-
ния (радиационная полимеризация) и электрического тока. По-
этому ионной полимеризацией можно получить большее число
полимеров по сравнению с радикальной.
В зависимости от знака заряда на концевом атоме растущей
цепи ионную полимеризацию подразделяют на анионную (отри-
цательный заряд) и катионную (положительный заряд).
Активные центры при ионной полимеризации являются по-
лярными образованиями, компоненты которых называются рас-
тущим ионом (R
+
и R
−
) и противоионом (А
−
или В
+
).
Характер связи между компонентами катализатора зависит от
их свойств и природы реакционной среды. Активный центр мо-
жет быть поляризованной молекулой, ионной парой или свобод-
ным ионом.
Например, при анионной полимеризации:
Различные типы ионных форм обладают различной реакци-
онной способностью. На вышеприведенное ионизационное рав-
новесие существенно влияет природа реакционной среды и по-
этому ионная полимеризация в отличие от радикальной сильно
зависит от реакционной среды. Вследствие зависимости ионной
47
полимеризации от природы растворителя проводить ионную по-
лимеризацию сложнее, чем радикальную полимеризацию, но она
обеспечивает получение стереорегулярных полимеров - полиме-
ров лучшего качества. Ионной полимеризации свойственно так-
же отсутствие реакций обрыва и передачи цепи, т.е. образование
«живых» полимеров.
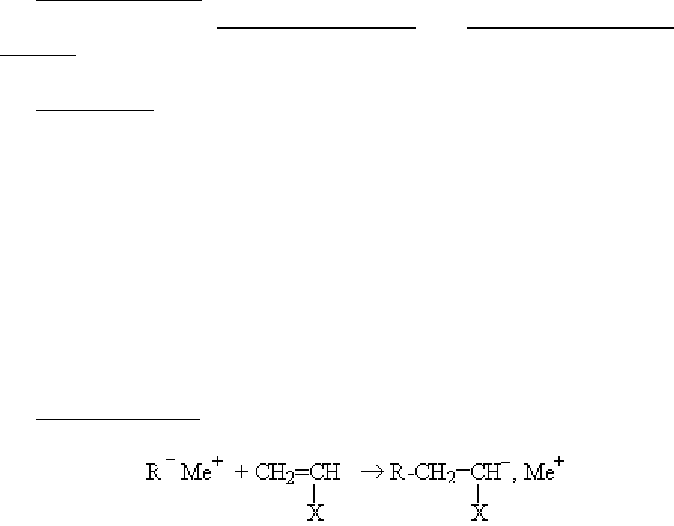
2.1.3.1. Анионная полимеризация
При анионной полимеризации конец растущей цепи заряжен
отрицательно и рост цепи можно изобразить следующим обра-
зом
∼М
n
−
+ M → ∼М
−
n+1
Катализаторами анионной полимеризации служат агенты ос-
новного характера - щелочные металлы
или производные метал-
лов I и II групп Периодической системы (амиды, алкоголяты, ал-
килы, ароматические комплексы).
Мономеры
для анионной полимеризации:
• ненасыщенные соединения СН
2
=СХY, где Х – группа,
снижающая электронную плотность у двойной связи (например,
CN, NO
2
, C
6
H
5
, -CH=CH
2
), Y – другая полярная группа.
• гетероциклические соединения (окиси, тиоокиси, лакто-
ны, лактамы, силоксаны),
• карбонилсодержащие соединения (например, альдегиды
полимеризуются по связи С=О).
Общая схема анионной полимеризации включает иницииро-
вание, рост, обрыв и передачу цепи (цепной процесс).
Инициирование
RMe
⇔ R
−
Me
+
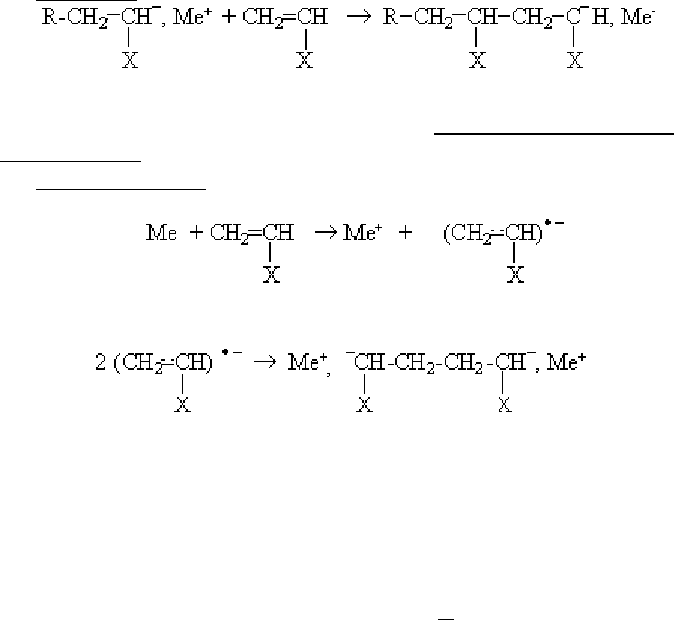
48
Рост цепи
Механизм анионной полимеризации под действием щелоч-
ных металлов:
Инициирование:
Анион-радикал возникает за счёт переноса
электрона от металла к мономеру.
Анион-радикалы рекомбинируют, образуя дианионы и рост
цепи идёт на обоих концах инициатора
Анионной полимеризации характерно отсутствие реакций
обрыва и передачи цепи, поэтому образуются «живые» полиме-
ры. После завершения полимеризации (после полного исчерпа-
ния мономера) активные центры сохраняются и при вводе новых
порций мономера продолжается рост цепи.
Скорость анионной полимеризации и ММ образующихся по-
лимеров определяются соотношениями
V
p
= [M][I
0
] (28) и Р = q ([M]/[ I
0
]), (29)
где q – конверсия.
При k
ин
>
k
р
цепи растут одновременно и образуется полимер
с узким ММР.
Скорость анионной полимеризации зависит от природы рас-
творителя и возрастает с увеличением его полярности.
Обрыв цепи возможен в следующих случаях:
1) За счёт реакции передачи цепи (путём отрыва активным
центром протона от растворителя или мономера)

49
Примером такой реакции является обрыв цепи при полиме-
ризация стирола под действием калия в жидком аммиаке.
2) При переносе гидрид-иона с конца цепи на противоион
илимономер
2.1.3.2. Катионная полимеризация
При катионной полимеризации конец растущей цепи заря-
жен положительно и рост цепи можно представить в виде
∼М
n
+
+ M → ∼М
+
n+
1
Катализаторами являются соединения кислотного характера:
протонные кислоты
(Н
2
SO
4
, HCl, H
3
PO
4
, HJO
4
, HF, HBr),
апротонные кислоты
- реагенты Фриделя – Крафтса с общей
формулой МеХ
n
, где Ме –металл, Х– галоген. Это кислоты
Льюиса. (BF
3
, BCl
3
, AlBr
3
, TiCl
4
, FeCl
3
). При использовании ап-
ротонных кислот необходим сокатализатор
– вода, спирты, про-
тонные кислоты, эфиры и др.)
Мономерами
для катионной полимеризации являются:
1) виниловые и диеновые мономеры, содержащие электро-
нодонорные заместители у двойной связи (например, изобутилен
СН
2
=С(СН
3
)
2
, α-метилстирол, изопрен). С увеличением элек-
троноположительности заместителя активность мономера в ка-
тионной полимеризации возрастает.
2) карбонилсодержащие соединения (по связи С=О), напри-
мер, формальдегид;
3) гетероциклические мономеры (с раскрытием цикла), на-
пример, оксиды олефинов.
50
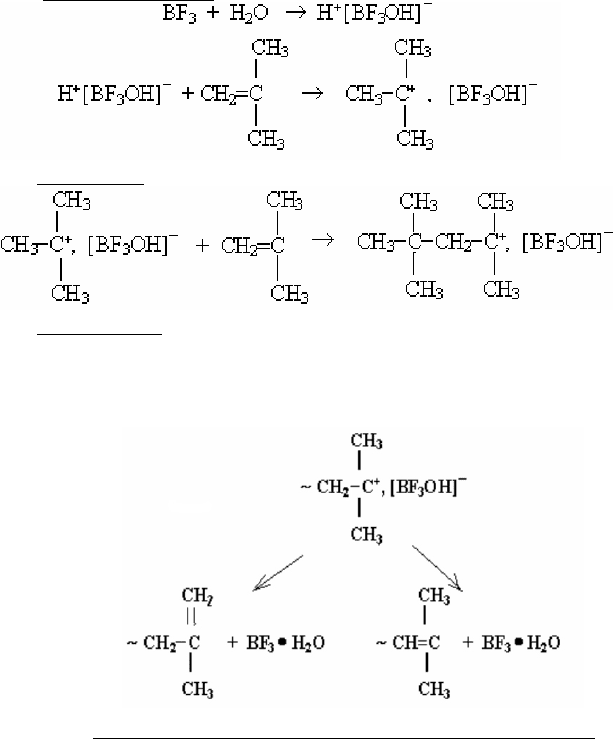
Схему катионной полимеризации на примере изобутилена в
присутствии ВF
3
и сокатализатора Н
2
О можно представить в
следующем виде:
Инициирование:
Рост цепи
:
Обрыв цепи
при катионной полимеризации – явление редкое,
но может протекать в следующих случаях:
1)
при переносе цепи с макроиона к противоиону или при
передаче цепи на мономер
.
2) при взаимодействии макроиона с противоионом
за счёт
перехода ионной связи в ковалентную
∼М
+
, А
+
→ ∼МА.
3) при присоединении анионного фрагмента противоиона к
карбокатиону.
