Курахтина Г.С. Общая электротехника: Учебное пособие

Подождите немного. Документ загружается.

чает, что напряжения на всех фазах потребителя изменятся причем напряжение будет ,

меньше на той фазе, где нагрузка больше.

Проследим за изменением положения точки

O на топографической диаграмме при

изменении нагрузки фазы А от короткого замыкания до холостого хода при неизменной

одинаковой нагрузке фаз В и С. При коротком фазы А точка будет иметь замыкании

потенциал точки А.

При холостом ходе (обрыв фазы А) точка рас-

середине отрезка, соединяющего В положится на точки

Рис. 2.50

и С на топографической диаграмме (рис. 2.50), как в так

этом случае фазы В и С соединены последовательно и

наход ым напряятся под линейн жением

U . Следовательно, при изменении нагрузки

фазы А от холостого хода до к откого замыкания точка будет скользить по медианеор

(рис. 2.52) треугольника. Это позволяет найти напряжения на всех фазах при любой ве-

личине нагрузки фазы А.

Рис. 2.52 Рис. 2.53 Рис. 2.51

Применяя это рассуждение для неравномерной нагрузки других фаз, нетрудно найти

положение точки топографической диаграмме, следовательно, и напряжения на фазах.

на

Четырехпроводная трехфазная система применяется для одновременного питания

как трехфазных, т фазных потребителей. ак и одно

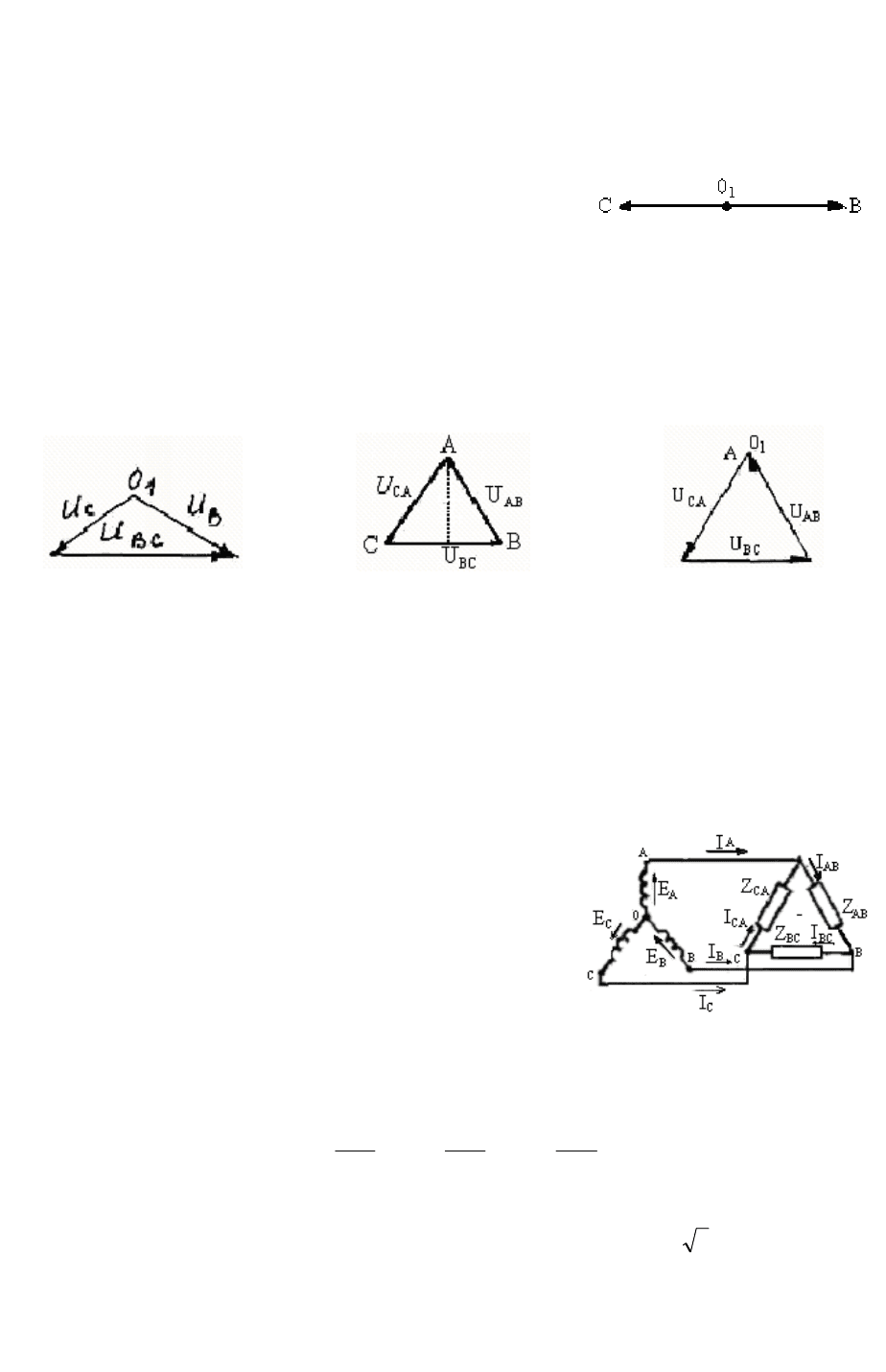
2.2.6. Соединение потребителей треугольником

Если потребители присоединить между линейны-

ми проводами, то они окажутся соединенными в виде

треугольника (рис. 2.54).

Трехфазная система при присоединении потребите-

лей треугольником имеет следующие свойства:

1. Система (потребители) нормально работает при

любом распределен нагрузки между фазами, так как ии

изменение нагрузки в одной фазе не сопровождается из-

менением токов в других фазах. Действительно, токи в потребителях (фазные токи) подсчи-

тываются по уравнениям, которые показываю

Рис. 2.54

т независимую работу потребителей (фаз):

I === ;;

BCAB

Сказанное справедливо при равенстве нулю сопротивлений линейных проводов.

2. При равномерной нагрузке линейные токи больше фазных в 3.

Доказательство. Напишем, например, для точки А уравнение по первому закону

Кирхгофа:

ABCAA

III

•••

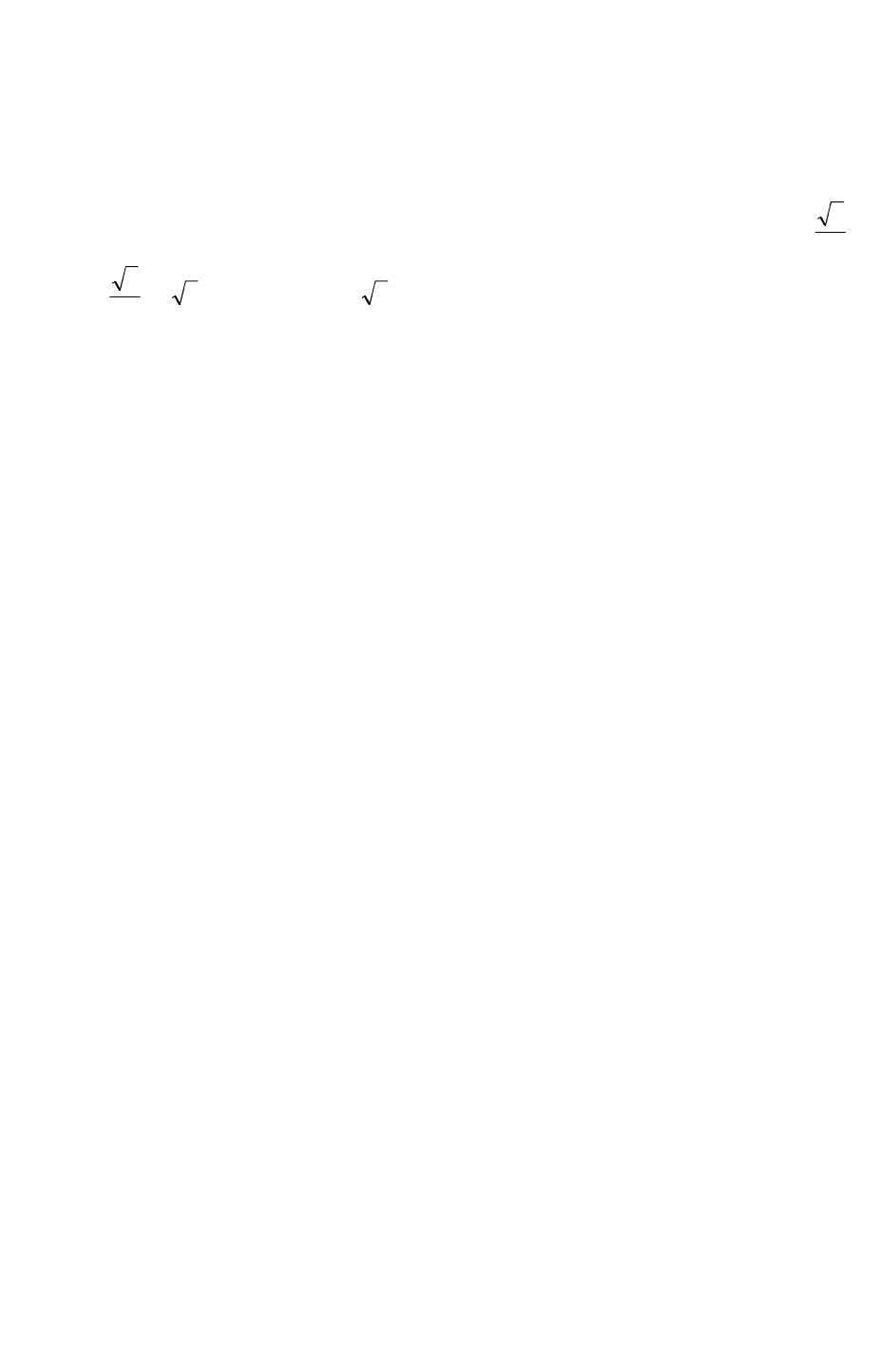
откуда

ACABA

III

•••

−= ,

т. е. линейный ток равен разности фазных токов. Так как

1200

••

CAAB

eIIeII

φφ

то

)120sin120(cos)0sin0(cos

1200

jIjIeIeIII

ЛA

+−+=−==

φφφφ

••

=−++

)

5,001( jjI

5,1(

eIjI

−

=−=

, или

= II 3.

Докажите это же для линейных токов

I и

I . Постройте векторную диаграмму

фазных и линейных токов, пользуясь правилами, указанными для напряжений.

2.2.7. Ненормальные режимы работы системы при соединении потребителей

треугольником

К данным режимам относятся:

1. Обрыв линейного провода. При равномерной нагрузке и обрыве линейного прово-

да на в два раза, так как фазах, присоединенных к этому проводу, напряжение уменьшится

эти фазы окажутся соединенными между собою последовательно, а по отношению к

третьей фазе – параллельно и включены под линейное напряжение. При ерной неравном

нагрузке напряжение на потребителях будет прямо пропорционально их сопротивлениям.

2. Короткое замыкание в потребителе означает короткое замыкание между линей-

ными проводами. В исправных потребителях не произойдет никаких изменений.

2.2.8. Соединение источников энергии звездой и треугольником

Соединять трехфазные источники энергии надо так, чтобы сумма ЭДС трех фаз

была равна нулю – это основное свойство трехфазной системы. Чтобы обеспечить ука-

занное правило при соединении звездой, надо объединить в одной точке О или все кон-

цы фаз (Х, У, Z) или их начала (А, B, С).

При ии треугольником к чке (вершине треуго при-соединен общей то льника) надо

соединить начало и конец соседних фаз. Ни в коем случае нельзя соединять в одной точ-

ке начала двух фаз или их концы. В этом случае произойдет опрокидывание одной из

фаз, что будет сопровождаться током короткого замыкания внутри генератора.

Чтобы убедиться в правильности указанных суждений, постройте векторную диа-

грамму ЭДС трех фаз. При этом считайте, что ЭДС имеет положительное направление

от конца фазы к ее началу.

2.2.9. Вращающееся магнитное поле трехфазного тока

Трехфазная система позволяет создать круговое вращающееся магнитное поле при

неподвижных обмотках магнитопровода. На неподвижном цилиндрическом магнито-

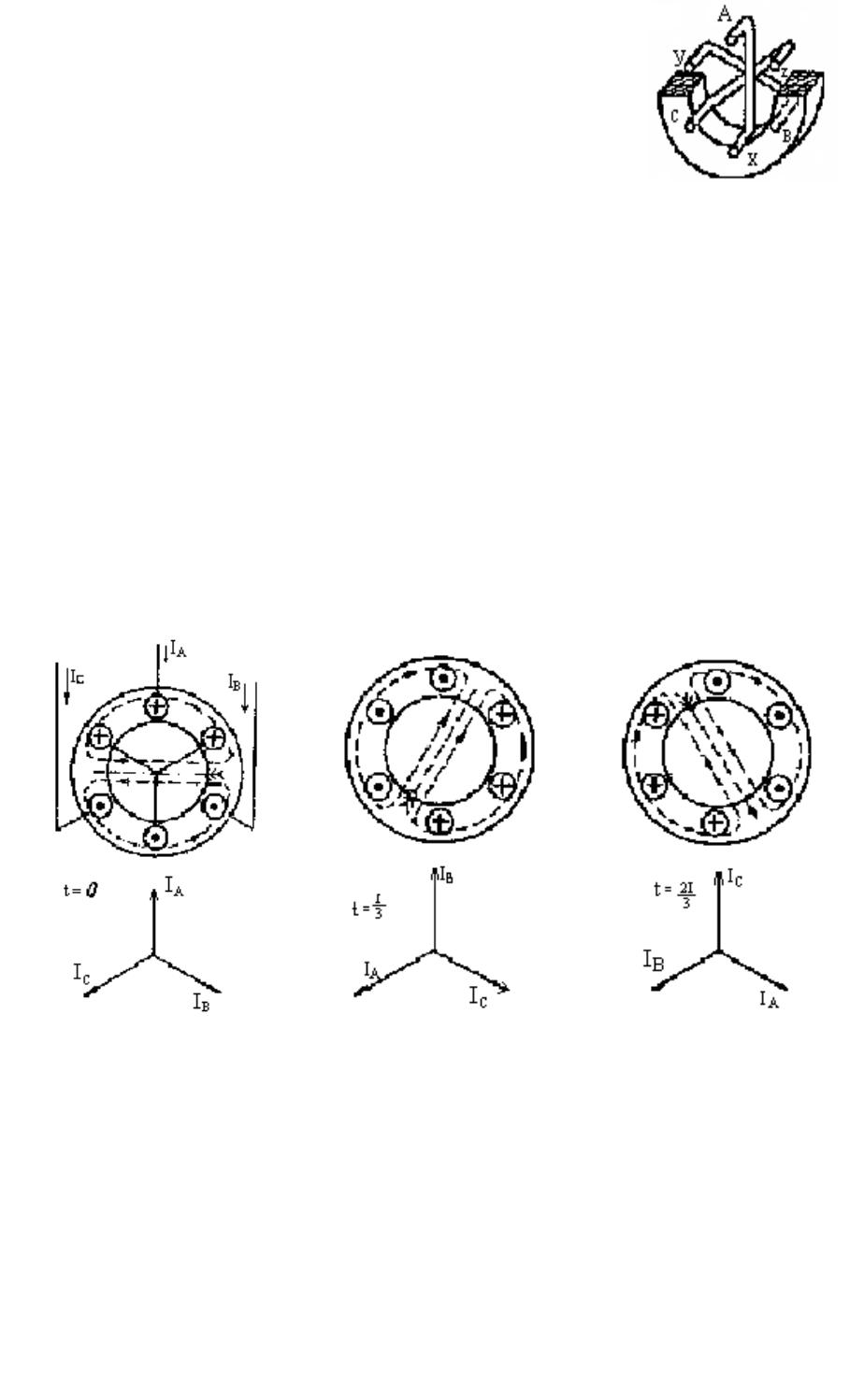
проводе в пазах с внутренней стороны размещают три

ки, р я про-асположенные в пространстве под углом 120°. Дл

стоты каждую обмотку можно представить как один разомк-

нутый виток (рис. 2.55). Обмотки соединены звездой (концы

соединены в одной точке, а начала присоединены к трехфаз-

ной сети).

Условимся считать ток положительным, если он течет от

начала обмотки к ее концу, а отрицательным – от конца к на-

чалу (можно взять и противоположное условие). Пусть при 0

t значение токов в фазах

соответствует векторной диаграмме (рис. 2.56, а). Согласно векторной диаграмме ток

.55

Рис. 2

первой фазе течет от начала к концу, а и третьей фазах – от конца к началу, во второй

что и отмечено крестиками и точками в соответствующих обмоток. Теперь, проводах

применив правило буравчика, изобразим картину магнитного поля (рис. 2.56, а), где ось

поля расположена горизонтально.

Через 1/3 периода токи в фазах будут соответствовать векторн дой иаграмме (рис.

2.56, б). Для этого же момента и по тем же правилам изображено магнитное поле над

векторной диаграммой. На рис. 2.56 видно, что ось магнитного поля повернулась за 1/3

периода на 120°.

На рис. 2.56, в показаны векторная диаграмма токов и магнитное поле через 2/3 пе-

ри сравнении картин магнитных полей (рис 2.56, а, б, в) видно, что магнитное риода. П .

поле вращается и в данном случае за один период делает один оборот. На этом принципе

и работа самых распространенных асинхронных двигателей. основана

а б в

Рис. 2.56

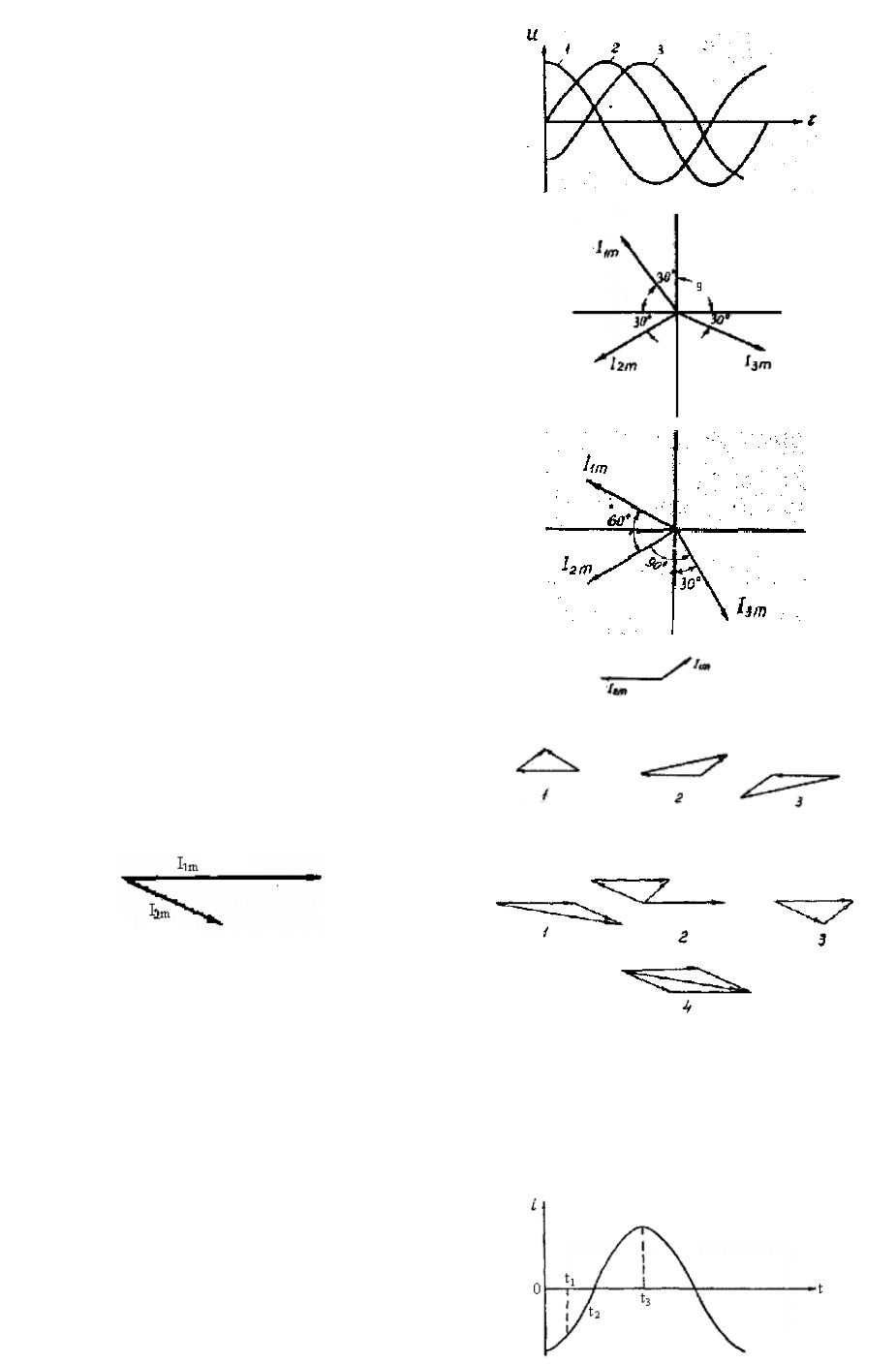
Практические задания

1. Какой график соответствует урав-

нению

)90sin(

+ω= tUu

2. Какому вектору тока соответствует

уравнение

)120sin(

+ω= tIi

соответствует

ур

3. Какому вектору тока

авнение

i = im sin( ωt – 150º)?

4. Два тока представлены вектора-

ми. На какой из трех приведенных век-

торных диаграмм дано решение уравне-

ния

321

iii =− ?

5. Два тока представлены векторами:

Напишите уравнения, показывающие,

какие действия произведены с токами со-

гласно нижеприведенным векторным диа-

граммам.

6. Что произойдет с величиною переменного тока в катушке, если ее фарфоровый

сердечник заменить латунным?

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

7. На рисунке приведен график тока

цепи какой , содержащей индуктивность. В

момент т наи- времени:

, tt или

t – буде

большая ЭДС самоиндукции?

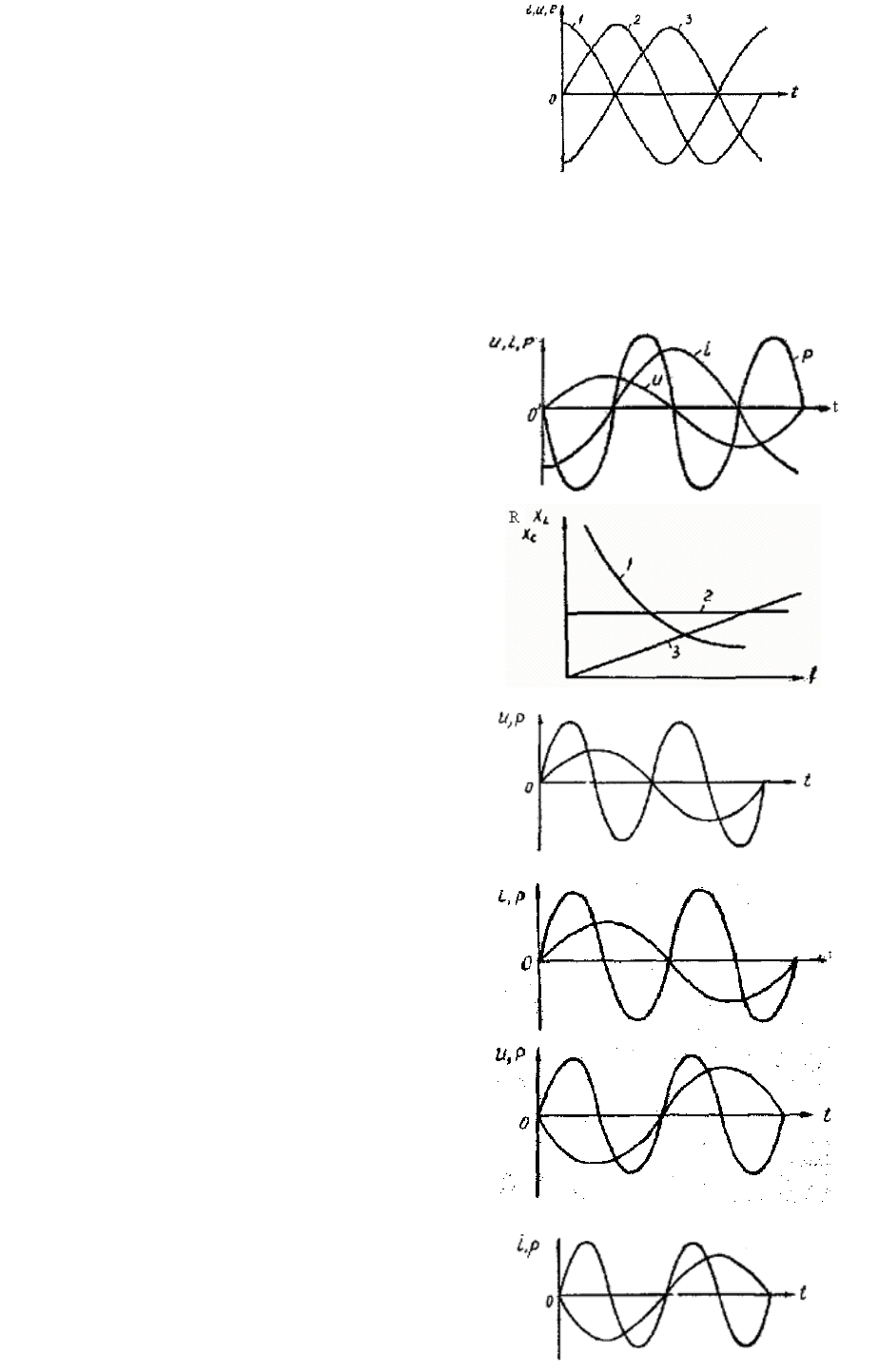
8. На рисунке показаны графики тока,

напряжения и электродвижущей силы са-

моиндукции для чисто индуктивной цепи.

Какой из этих графиков представляет ЭДС?

9. Что произойдет с величиной переменного тока, если в катушке ее фарфоровый

сердечник заменить на стальной?

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

10. На рисунке показаны графики на-

пряжения, тока и мощности для цепи пе-

ременного тока. Что включено в эту цепь?

Ответ: 1 тив ое сопротивление; ) ак н

2) индуктивность;

3) емкость.

11. На рисунке показаны графики из-

менения активного, индуктивного и емко-

стного сопротивлений как функции часто-

ты. Какой из этих графиков представляет

емкостное сопротивление?

12. На рисунке показаны графики на-

пряжения и мощности цепи переменного

тока. то включено в эту цепь? Ч

Ответ: 1) активное сопротивление;

2) индуктивность;

3) емкость.

13. На рисунке показаны графики то-

ка и мощности цепи переменного тока. Что

включено в эту цепь?

Ответ: 1) активное сопротивление;

2) индуктивность;

3) емкость.

14. На рисунке показаны на-графики

пряжения и мощности цепи переменного

тока. Что включено в эту цепь?

Ответ: 1) активное сопротивление;

2) индуктивность;

3) емкость.

15. На рисунке показаны графики то-

ка и мощности цепи переменного тока. Что

включено в эту цепь?

Ответ: 1) активное сопротивление;

2) индуктивность;

3) емкость.

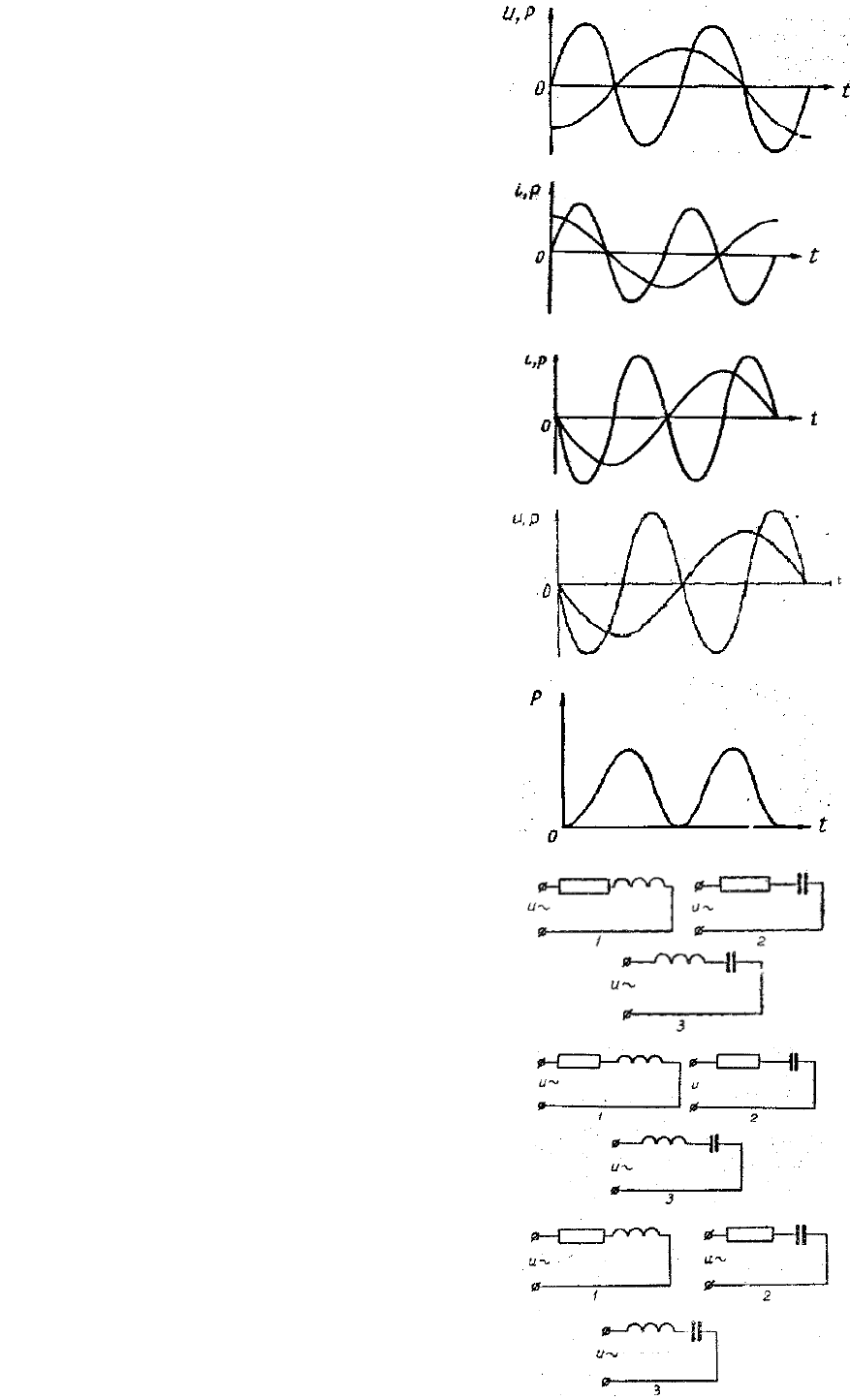
16. На рисунке показаны графики на-

пряжения и мощности цепи переменного

тока. Что вк элючено в ту цепь?

Ответ ление: 1) активное сопротив ;

2) индуктивность;

3) емкость.

17. На рисунке показаны графики то-

ка и мощности цепи переменного тока. Что

включено в эту цепь?

Ответ: 1) активное сопротивление;

2) индуктивность;

3 . ) емкость

18. На рисунке показаны графики то-

ка и тока. Что мощности цепи переменного

включено в эту цепь?

Ответ: 1) активное сопротивление;

2) индуктивность;

3) емкость.

19. На рисунке показаны графики на-

пряжения и мощности цепи переменного

тока. Что включено в эту цепь?

Ответ: 1) активное сопротивление;

2) индуктивность;

3) емкость.

20. На рисунке показан график мощ-

ности включе- цепи п . Что еременного тока

но в эту цепь?

Ответ: 1) активное сопротивление;

2) индуктивность;

3) емк . ость

21. Какой цепи могут соответствовать

следующие уравнения:

)120sin(

+ω= tUu

)30sin(

+ω= tIi

22. Какой цепи могут соответствовать

уравнения

)30sin(

+ω= tUu

)90sin(

+ω= tIi

23. Как ответсой цепи могут со твовать

уравнения

)60

−

sin(ω= tUu

)90

−t

sin(ω= Ii

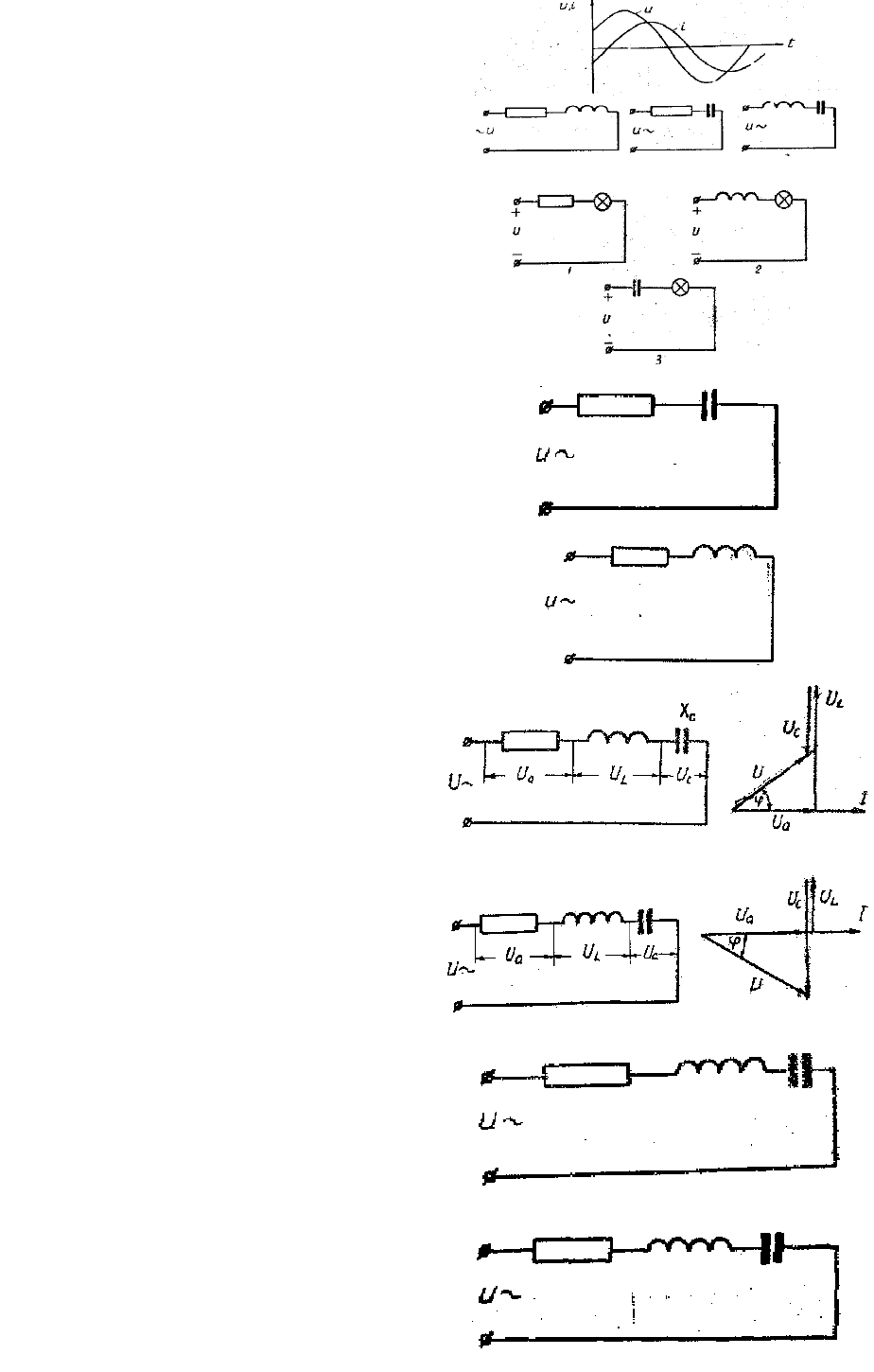
24. Для какой цепи возможны приве-

денные графики тока и напряжения?

1 2 3

25. В какой из трех схем лампочка

горит более ярко?

26. Что произойдет с активной мощ-

ностью цепи, если увеличить емкость кон-

денсатора?

Ответ: 1) увеличится;

2) уменьшится;

3) не измени

тся.

27. Что произойдет с

cos , если

уменьшить индуктивность?

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

28. На рисунке приведена электриче-

ская цепь и рядом дана векторная диа-

грамма напряжений при заданной частоте

сети. Что произойдет с напряжениями

и углом ϕ , если увеличить ча

UUa,

с-

тоту при неи ии цепи? зменном напряжен

а б

29. На рисунке приведены электриче-

ская цепь (а) и векторная диаграмма на-

пряжений (б). Что произойдет с напряже-

ниями

LCa

UUU ,, и углом

, если

умен а-ьшить емкость при неизменном н

пряжении сети?

30. Для изображенной на рисунке

схемы известно, что

XXr <<

. Нари-

суйте векторную диаграмму напряжений

для э я того случая. Как изменится векторна

диаграмма, стоту при если увеличить ча

прежнем нап и? ряжении сет

31. Что происходит с напряжением на

активном сопротивлении, если уменьшить

индуктивность при

Ответ: 1) увеличится;

2) уменьшится;

3) не измени

тся.

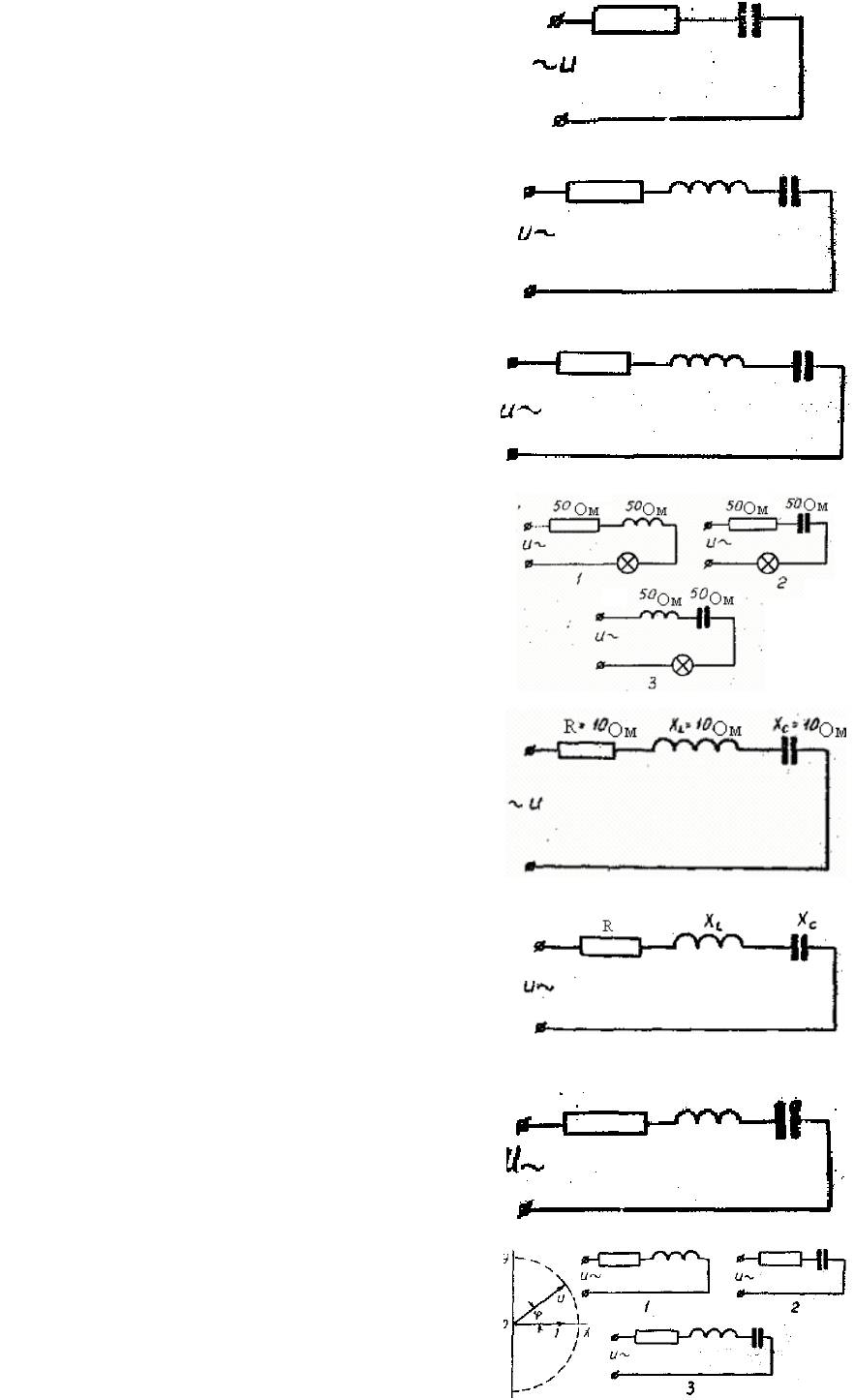
32. Что произойдет с

cos

, если

уменьшить емкость?

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

33. Чт ит с напряжениемо происход

на активном сопротивлении, если частота

увеличивается и Х > 0?

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

34. Что происходит с напряжением на

активном сопротивлении, если частота

увеличивается и

0<X

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

35. В к ех схем лампакой из тр очка

горит более ярко?

36. Что произойдет с

ϕcos

, если из-

менить индуктивное сопротивление?

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

37. Что произойдет с напряжением на

активном сопротивлении, если уменьшить

емкость при

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

38. Цепь настроена в резонанс. Что

происходит с напряжением на активном со-

противлении, если увеличить индуктивность?

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

39. Для какой из электрических схем

возможно изменение угла ϕ от –90° до

+90° при постоянной величине напряжения

и изменении частоты?

40. Что произойдет с током в емко-

сти, если увеличить индуктивность?

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

41. В какой лампочке яркость горения

увеличивается с увеличением частоты?

42. Для изображенной схемы (а) дана

векторная ди ). аграмма токов (б

Как изменятся токи, если увеличить

часто п и не нату при режней вел чи пряже-

ния? Нарисуйте векторную диаграмму.

а б

43. В какой лампочке яркость горения

уменьшается с увеличением частоты?

44. На рисунке показан график изме-

нения полного сопротивления цепи пере-

менного тока как функция частоты. Как

включены в этой цепи индуктивность и

емкость?

Ответ: 1) последовательно;

2) параллельно.

45. На рисунке показан график изме-

нения полного сопротивления цепи пере-

менног ф нкция час ы Как о тока как у тот .

включены в этой цепи индуктивность и

емкость?

Ответ: 1 последовательно; )

2) параллельно.

46. Что произойдет с ϕcos , если из-

менить индуктивное сопротивление?

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

47. В какой схеме лампочка горит ярче?

а б

48. Для цепи, изображен схеме, ной на

известно, что

1 LC

RXXR =>=

Нарису иагйте векторную д рамму ак-

тивных и реактивных токов ветвей и обще-

го тока. Как изменятся эти токи, если уве-

личить частоту? Покажите это на другой

векторной диаграмме.

49. Что пряже произойдет с на нием на

активном со ли противлении, ес увеличить

индуктивность?

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

50. В какой из трех схем наблюдается

наибольший од общий ток при инаковом

напряжении источника?

51. На приведенной здесь схеме необ-

повысить

cos

до 1, но ходимо напряжение

на прежним. потребителях должно остаться

Нарису конденсатора йте схему включения

для о овнябеспечения данного ур , а также

векторную диаграмму, на которой надо по-

казат енсатора. ь необходимый ток конд

52. Приведена векторная диаграмма

для остоящей из электрической цепи, с

дву ветвей. При этом из-х параллельных

вестно следующее:

Ом10Ом,8,,

21221

==== zRIIII

papa

Нарисуйте электрическую схему цепи

и определите

211

,, XRX .

53. Потребители рассчитаны на оди-

наковое напряжение и одинаковую мощ-

ность. Чему равен ток нулевого провода,

если ток A10

=I ?

Ответ: 1) 10 А;

2) 17,3 А;

3) 0.

54. Что произойдет с током

I , если

вторую лампу заменить на л мпу большей а

мощности того же напряжения?

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.