Курахтина Г.С. Общая электротехника: Учебное пособие

Подождите немного. Документ загружается.

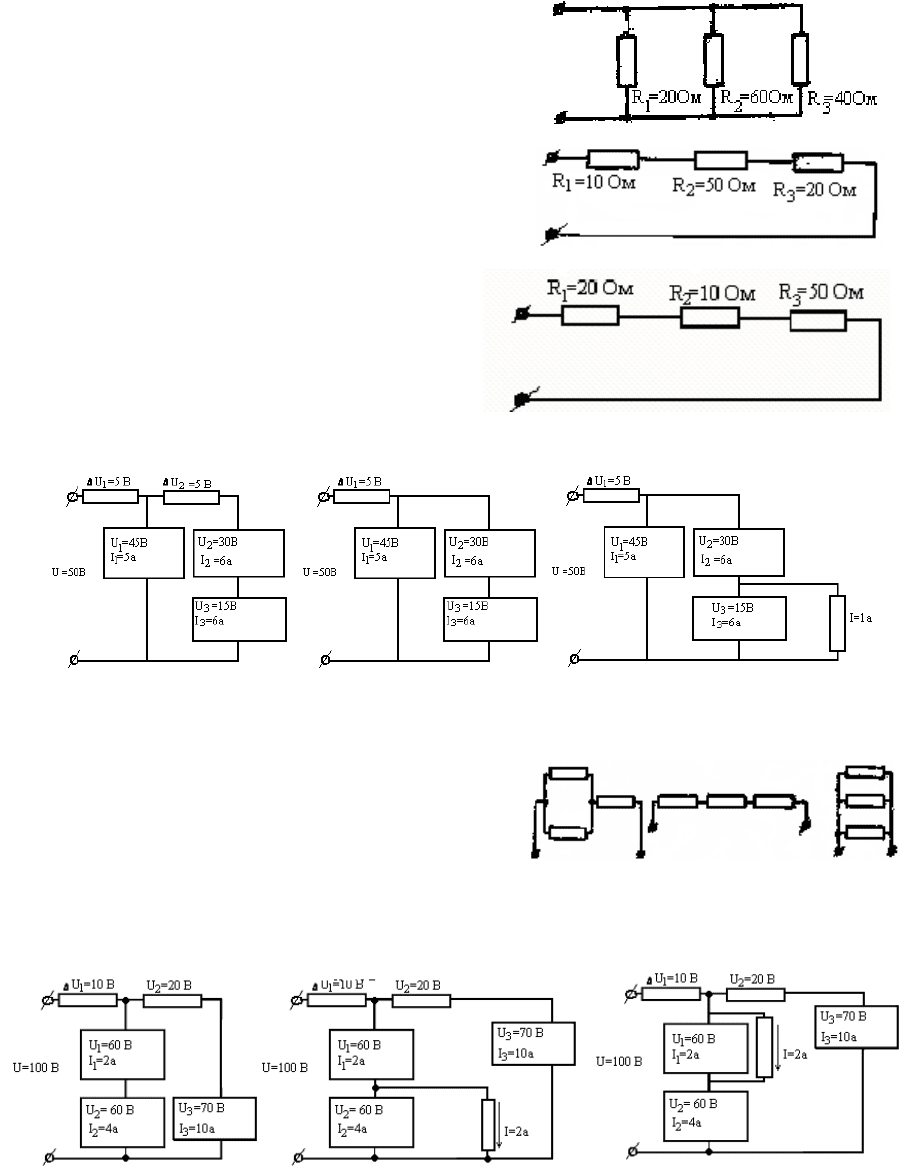
38. На каком участке цепи будет наи-

больший ток?

39. На каком из трех сопротивлений

будет наибольшее напряжение?

40. На каком из трех сопротивлений

выделяется н ергии?аибольшее количество эн

собрана правильно? 41. Какая из этих схем

общем то-

схемах

а б

42. В какой из трех схем мощность бу-

дет н овом

ке в цепи, ения в

одинаковые?

аибольшая при одинак

если сопротивл

Ответ: 1) схема

а;

2) схема

б;

3) схема

в.

а б в

собрана правильно? 43. Какая из этих схем

44. По мере горения электрической ла

б в

мпочки часть металла с поверхности нити

накал нить делается тоньше. Как изменяется вследствие этого

мощность ла

Ответ:

2) уменьшается;

3) не изменяется.

а лампы испаряется и

мпы?

1) увеличивается;

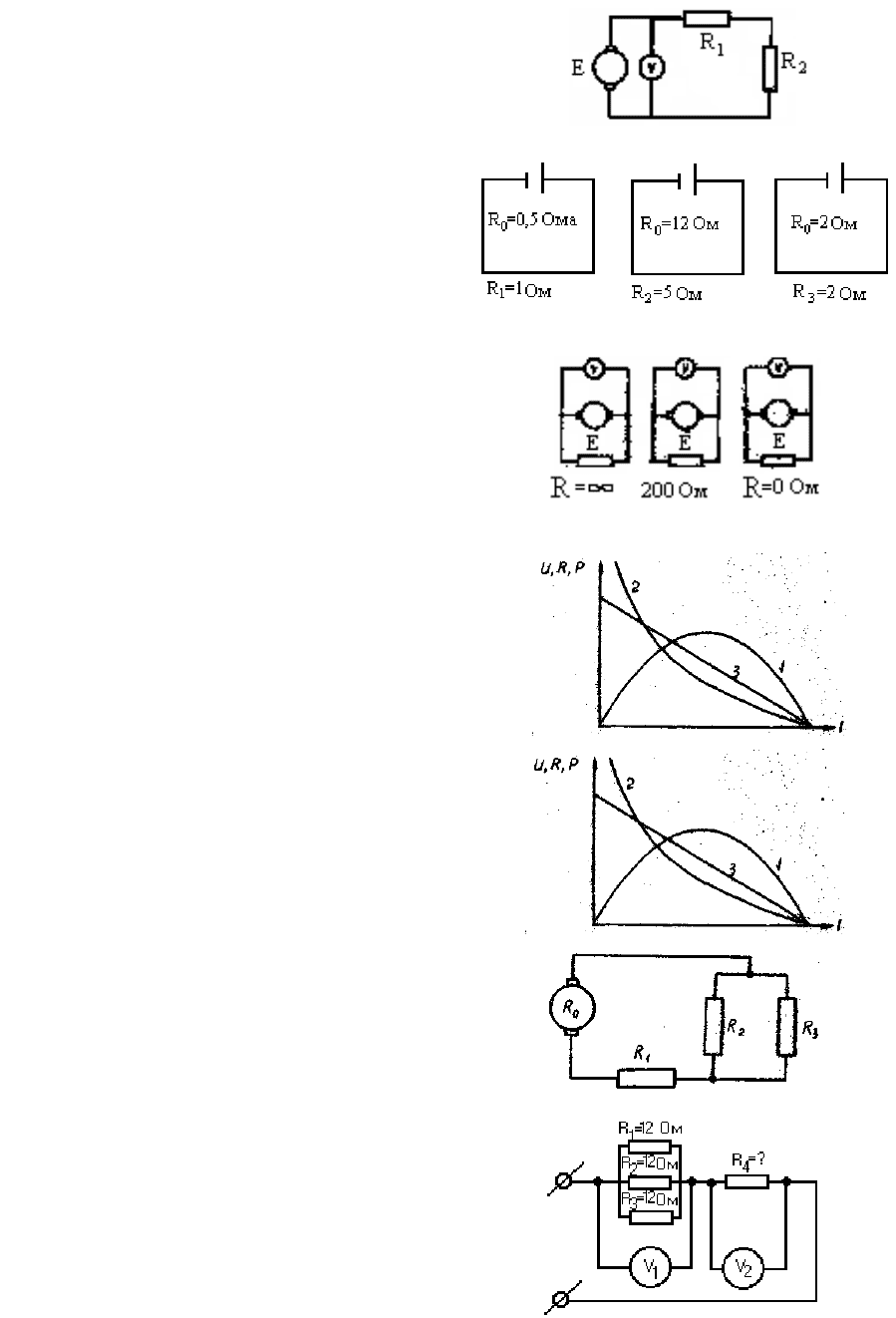
45. Что произойдет с напряжением ис-

точника, если сопротивление

E st.)

Ответ: 1) увеличится;

2) уменьшится;

увеличит-

ся? ( = con

3) не изменится.

46. Какой источник отдает максимум

мощности?

а б в

показы-

вает

47. В какой схеме вольтметр

электродвижущую силу источника?

а б в

графики из-

от холо-

стого . Какая

из э

ния

48. На чертеже показаны

менения напряжения, сопротивления

мощности при изменении нагрузки

хода до короткого замыкания

ти

х кривых изображает график измене-

апряжения?

49. На чертеже показаны графики из-

менения напряжения, сопротивления и

мощности при изменении нагрузки от холо-

стого

гра-

фик

хода д замыканияа короткого

Какая из ых изображает

этих кри

зменения мощности?

50. Что произойдет с током в сопро-

тивлении R

, если уменьшить сопротивле-

ние R

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

51. Какой величины будет сопротив-

, если оба вольтметра показываютление

одинаковое напряжение?

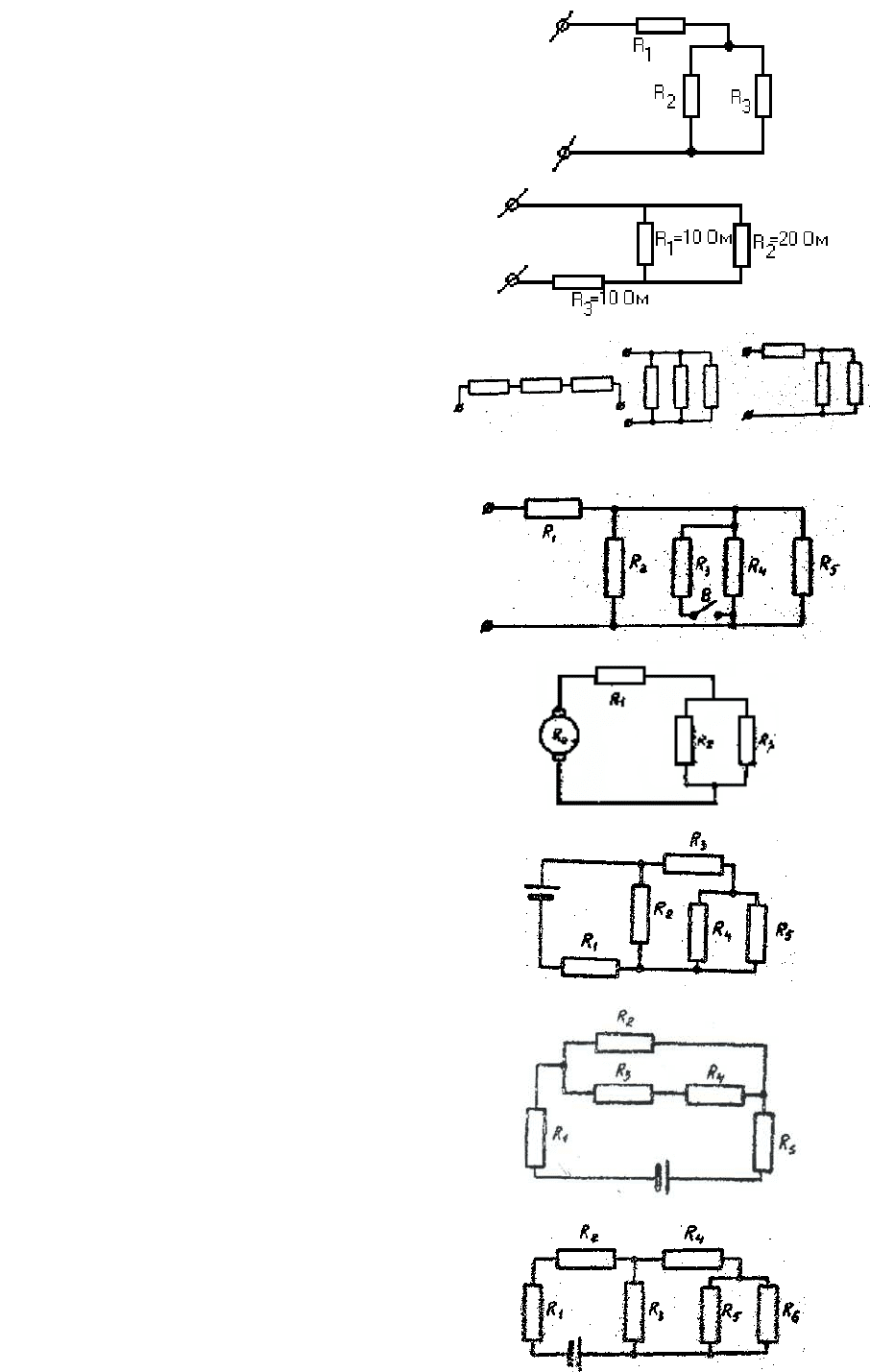
52. Сопротивления R

, R

имеют

одинаковую величину и соединены по схе-

ме, изображенной на рисунке. На сопротив-

лени ж тепла. Сколь-и R

выделилось 100 Д

ко выделил же время нось тепла за это

сопротивлении R

53. На каком из трех сопротивлений

выделяется наибольшее количество тепла?

54. Какая из трех схем выделяет наи-

большее количество энергии, если сопро-

тивления в схемах одинаковые?

а б в

55. Что произойдет с напряжением на

потребителе R

, если замкнуть выключа-

тель В?

Ответ: 1) увеличится;

2) уменьшит я;

3) не изменится.

56. Что произойдет с напряжением ис-

точника, если уменьшить сопротивление

? (E = const.)

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

57. Как соединены между собой со-

противления на схеме?

Как изменятся (увеличатся или

уменьшатся) токи в каждом сопротивлении,

если сопротивление R

уменьшить при не-

изменном напряжении источника?

у собой со-

личатся или

58. Как соединены межд

противления

Как

уменьшатся) токи в каждом

если

на схеме?

изменятся (уве

сопротивлении

сопротивление

увеличить при неиз-

менном напряжении источника?

собой со-

к изменятся

) токи в каж-

отивление

напряжении

59. Как соединены между

противления на схеме? Ка

(увеличатся или уменьшатся

дом сопротивлении, если сопр

уменьшить при неизменном

источника?

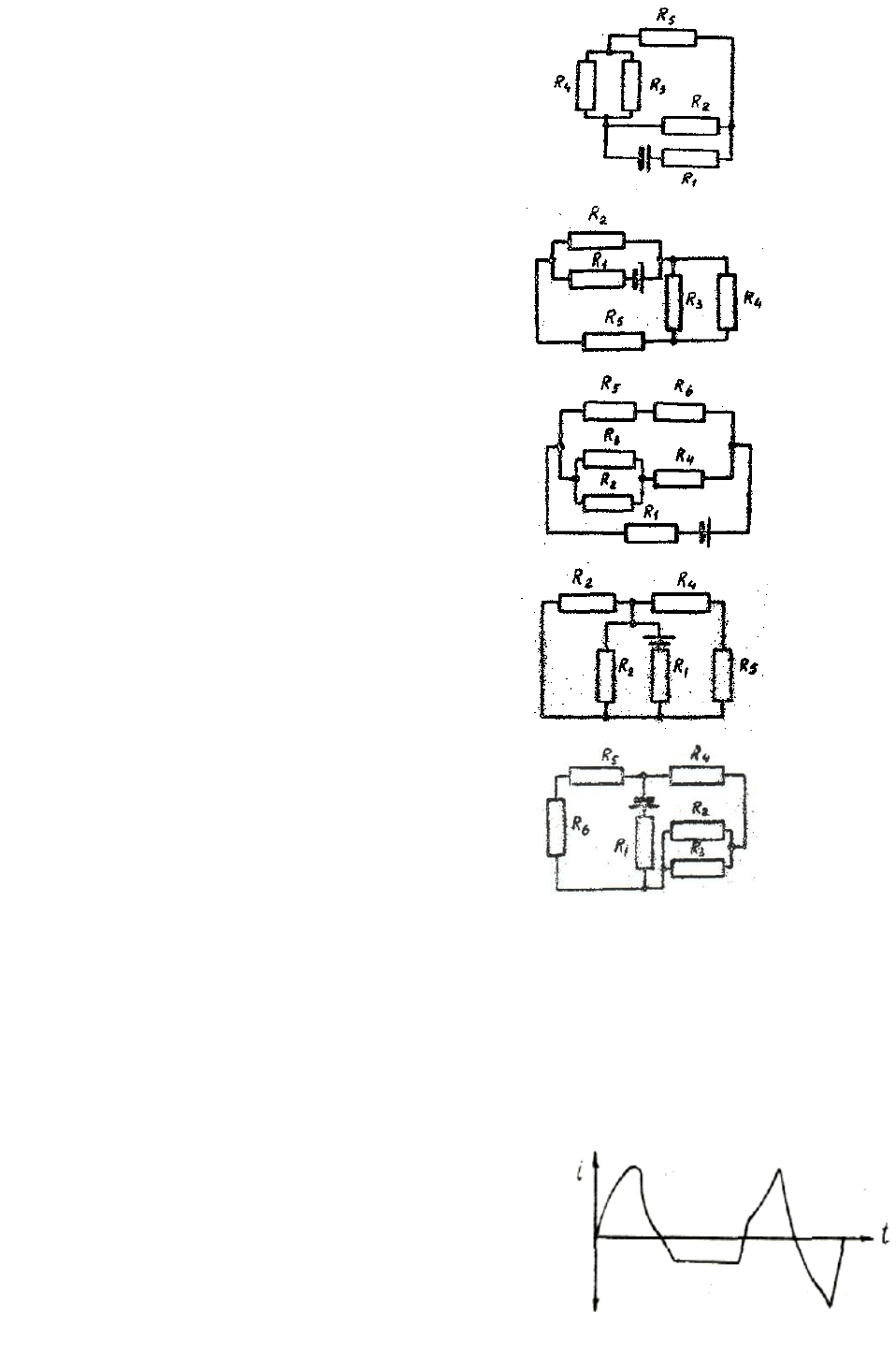
60. Как соединены между собой со-

противления на схеме? Как изменятся

(увеличатся или уменьшатся) токи в каж-

дом сопротивлении, если сопротивление R

увеличить при неизменном напряжении

источника?

против к изменятся

(ув ) токи в каж-

дом отивление

ув напряжении

ист

61. Как соединены между собой со

ления на схеме? Ка

еличатся или уменьшатся

сопротивлении, если сопр

еличить при неизменном

очника?

62. Как соединены между собой со-

против Как изменятсяления на схеме?

(ув ся) токи в каж-еличатся или уменьшат

дом о сопротивлении, если с противление R

уменьшить при неизменном напряжении

источника?

63. Как соединены между собой со-

противления з на схеме? Как и менятся (уве-

личатся или уменьшатся) токи в каждом со-

противлении, если сопротивление R

увеличить при неизменном напряжении ис-

точника?

64. Как соединены между собой со-

против ак изменятсяления на схеме? К

(увеличатся или уменьшатся) токи в каж-

дом сопротивлении, если опрот ение R с ивл

увеличить при неизменном напряжении

источника?

И ТЕХФАЗНЫЙ ТОКИ

ный ток

деления

Глава 2. ОДНОФАЗНЫЙ

2.1. Перемен

2.1.1. Общие понятия и опре

Переменный ток – это ток, изменяющийся с тече-

нием времени по величине и направлению.

В общем случае переменный ток – сложный ток,

изменения которого не подчиняются какой-либо зако-

номерности (рис. 2.1).

На практике чаще всего приходится иметь дело с

периодическ м током. Периодический ток – и это пере-

менный ток,

Рис. 2.1

изменения которого повторяются периоди-

чески азываемые периодом. Период обозначается через равные промежутки времени, н

буквой Т (рис. 2.2).

Периодический ток вообще – ток слож

мыми различными, но у него уже есть опред

дый новый ерио он изменяется точно так ж

ной формы. Его изменения могут быть са-

еленная закономерность изменения: в каж-

п д е, как и в предыдущий.

В технике обычно имеют дело с самым про-

стым периодическим током – синусоидальным,

которого совершаются по закону си-

Под термином «переменный ток» понимают

нусоидальный.

изменения

нуса.

ток си

Все токи, изменяющиеся по любому друго-

му закону (несинусоидальному), называют неси-

нусои

Рис. 2.2

дальными токами.

На рис. 2.3. показан график синусоидально-

го то ичины, характеризующие переменный ток. ка, на котором отмечены некоторые вел

Значения тока в данный момент времени (например, ), представленные на в

4321

,,, tttt

рис. 2.3 ординатами, которые заключены между графиками и осью абсцисс, назы- тока

ваются мгновенными значениями

4321

,,, iiii

. Мгновен ия тока, напряжения, ные значен

ЭДС обозначаются малыми буквами eui ,, . Среди значений наибольшее мгновенных

значение синусоидальной величины - называет

ся амплитудой. Амплитуды тока, напряжения

и ЭД н-С обозначаются большими буквами с и

дексом

),,(

mmm

EUIm

Период – это отрезок времени, по исте-

чении которого изменения периодических ве-

личин повторяются. Период измеряется в се-

кундах (с). Число периодов за 1 с называется

часто ся той, обозначается буквой

и измеряет

в герцах (

При вращении проводника в равномер

Рис. 2.3

ном магнитном поле с постоянной угловой

скоростью в проводнике индуктируется синусоидальная ЭДС e = tE

ωsin . ω

гнитное поле двухполюсное, то время одного оборота рамки равно ериоду Т. пЕсли ма

Если генератор имеет пар полюсов, то за один оборот совершается . периодов

Уравнение Э . Все зависит от ДС (тока или напряжения) может иметь и другой вид

того, как выражать угловую скорость

. Для двухполюсного генератора угловую ско-

рость можно определить так:

360

,2,

=ωπ=ω

=ω

тогда гой величины будут иметь следующий вид: уравнения синусоидальной ЭДС или дру

.2sin,

sin,sin ftEet

EetEe

mm m

π=

=ω=

Если вращать в магнитном поле не одну, а несколько рамок, жестко скрепленных

между собою под некоторыми углами ,,,

321

то ЭДС, индуктируемые в рамках, бу-

дут о удут достигать одноименных значетличаться друг от друга только тем, что они б -

ний (одинаковых по названию) не одновременно, а в различные моменты времени.

В этом случае говорят, что синусоидальные величины не совпада – между ют по фазе

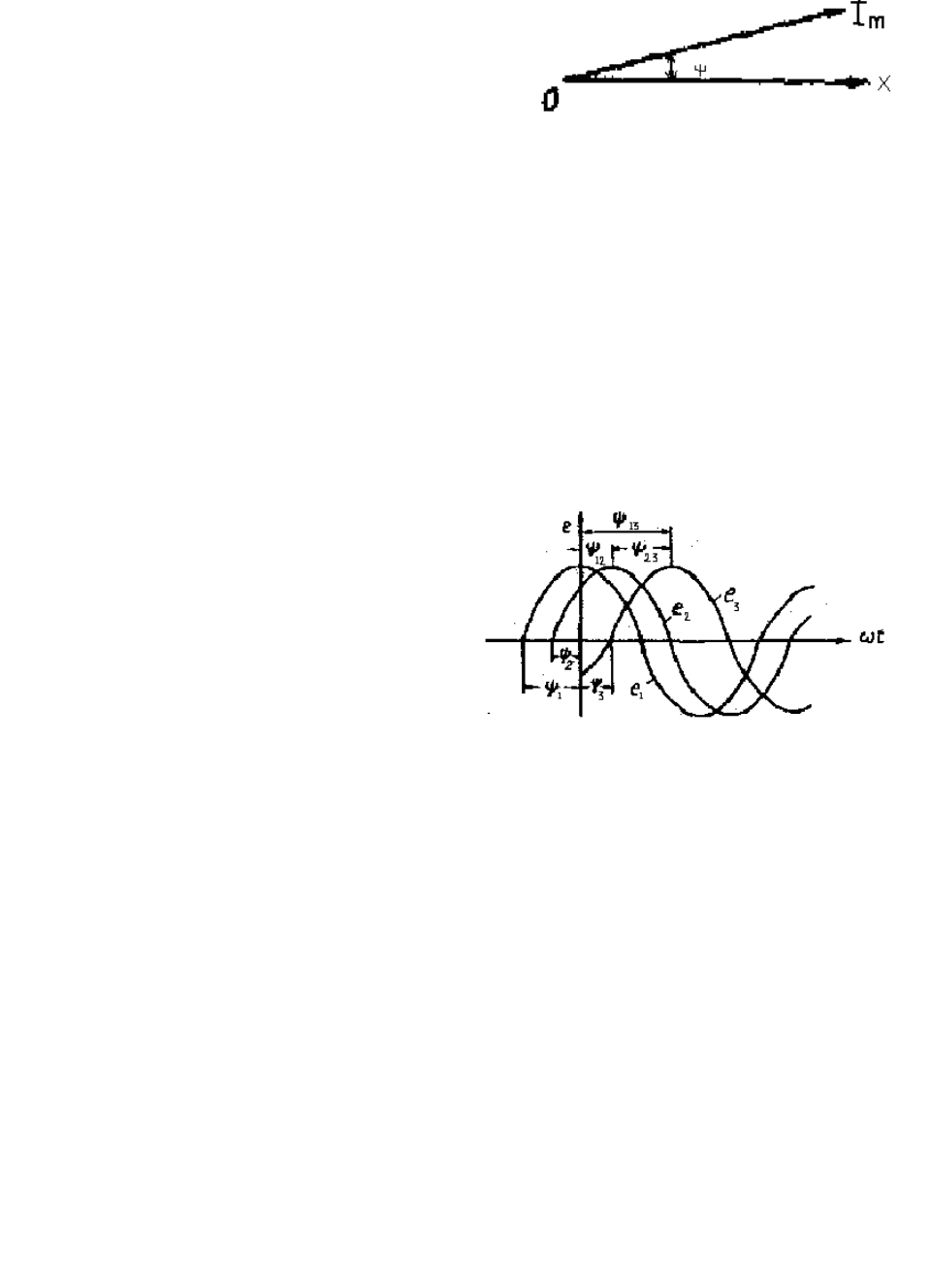
ними есть сдвиг фаз. Такие синусоидальные

чины в начальный момент време

ни ( 0

t ) будут

иметь разные значения.

Если синусоидальные величины имеют оди-

наковую частоту, но одноименных значений дос-

Рис. 2.5

тигают в различные моменты времени, то они не

совпадают по фазе – между ними есть сдвиг фаз.

Угол, определяющий значения синусоидальной величины в начальный момент

времени, называется начальной фазой.

Уравнения синусоидальных величин, сдвинутых по фазе, имеют следующий вид:

)sin(),n(

332

si),sin(

211

ψ+ω= EetEe

tEet

В этих уравнен ы иях угл

321

ψψ яв фаз ляются начальными фазами. Угол сдвига

равен разности начальных фаз:

322331132112

−

ψ−ψ=

Угол, определяющий значение синусоидальной величины в данный момент времени,

называется фазой. В приведенных выше уравне первой ЭДС (е

) фазой является ниях для

угол

ψ+ωt

, для второй ЭДС (е

) – угол

ψ+ωt

, для третьей ЭДС (е

) – угол

ωt

На рис. 2.4 приведены графики синусои-

дальных величин, сдвинутых по фазе, отмече-

ны углы на учальных фаз и глы сдвига фаз.

Любая периодическая величина полно-

стью может быть охарактеризована некото-

рыми постоянными величинами, которые в

этом случае называются ее параметрами. Так,

параметрами инусоидальных величин а, с (ток

напряжения, ДС и др.) являются амп а,

Рис. 2.4

Э литуд период или частота, начальная фаза или

сдвиг величины, то мы о ней все. фаз. Если мы знаем параметры синусоидальной

2.1.2. Векто

знаем

рное изображение синусоидальных величин

В основу векторного изображения синусоидальных величин положено следующее:

при вращении вектора длиною, равной амплитудному значению синусоидальной вели-

чины, против часовой стрелки со скоростью

проекция вектора на вертикальную ось

изменяется по закону синуса, т. е. по тому же закону, по какому изменяется мгновенное

значение синусоидальной величины. Для векторного изображения синусоидальной ве-

личины вектор, равный ее амплитудному значению, откладывают к горизонтальной оси

под углом, равным начальной фазе.

)sin(

tIi

, Ток, представленный уравнением векторно изображается так, как

это показано на рис. 2.5.

На рис. 2.6, б, в показано, как векторно находить сумму дв х синусоидных вели-у

чин, представленных векторами (рис. 2.6, а), применяя правило параллелограмма и тре-

угольника (многоугольника).

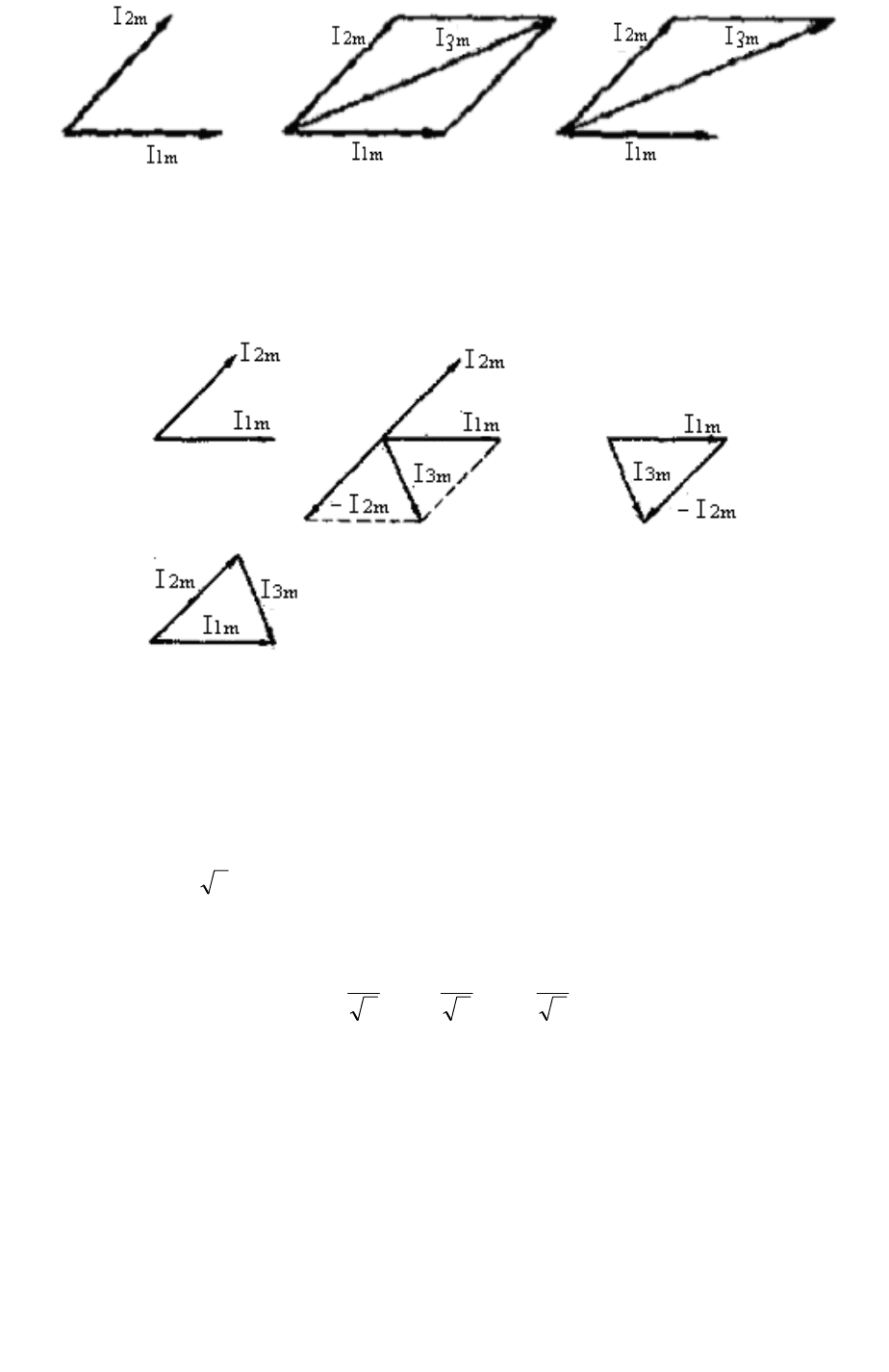
а б в

Рис. 2.6

На рис. 2.7, сину ве-соидальныхб, в, г показаны три способа нахождения разности

личин, представленных векторно на рис. 2.7, а.

Рис. 2.7

Эффективность действия переменного тока оценивае называемым дейст-тся так

вующим, или эффективным, его значением.

Действующее значение переменного тока равно такому значению постоянного тока,

которое вызывает такой же тепловой эффект, как и рассматриваемый переменный ток.

Для синусоидальных величин действующее значение равно амплитудному значе-

. нию, деленному на

Действующие значения тока, напряжения, ЭДС обозначаются такими же буквами,

как и для постоянного тока:

mmm

I ===

2.1.3. Электрическое сопротивление

Сопротивление понимается как некоторое препятствие прохождению электрическо-

го тока. Эти препятствия могут иметь различную физическую сущность, а следовательно,

и характер сопротивления бывает разли ким бы ни был характер сопро-чным. Однако ка

тивле ения истония, на нем всегда теряется часть напряж чника, что и является признаком

наличия сопротивления на данном участке цепи. Из этого следует, что если на участке це-

пи теряется часть напряжения источника, то этот участок обладает сопротивлением.

Напряжение на участке цепи может теряться по разным причинам. Одна из них со-

стоит в том, что на участке цепи электрическая энергия преобразуется в другую форму

энергии (тепловую, световую и т. д.). В данном случае говорят, что этот участок облада-

ет активным сопротивлением. Для постоянного тока сопротивление определяется нали-

чием физических носителей тока – электрических зарядов, способных перемещаться под

действием сил электрического поля. Если носителей тока (свободных электронов в твер-

дых телах, ионов в жидкостях и газах) в единице объема данного вещества много, то те-

ло обладает небольшим сопротивлением. Если же этих носителей тока мало, то тело об-

ладает большим сопротивлением (при прочих равных условиях), так как во втором

случае ток будет меньше, чем в первом.

Активное сопротивление проводника переменному току больше сопротивления по-

стоянному току из-за явления поверхностного эффекта – оттеснения тока из центра про-

водни верх ости. т у уменьшается пл перечного сечения ка к его по н Благодаря э ом ощадь по

проводника для переменного тока по сра с постоянным током. внению

Практически активное сопротивление подсчитывается по формуле

R =

где – мощность, потребляемая на данном участке цепи;

– действующее значение переменного тока.

Активное сопротивление обозначается буквой R, а на чертеже знаком .

2.1.4. Индуктивное сопротивление

Если на участке цепи теряется часть напряжения источника на уравновешивание

ЭДС самоиндукции, то говорят, что этот участок обладает индуктивным сопротивлением.

Электродвижущая сила самоиндукции согласно правилу Ленца противодействует

всякому изменению тока. Если по цепи течет переменный ток, то причиной возникнове-

ния ЭДС самоиндукции является именно изменение тока. ЭДС самоиндукции препятст-

вует прохождению переменного тока, а вне мы воспринимаем это как наличие неко-шне

торого сопротивления в данной цепи.

Конечно, не надо отождествлять величину ЭДС с величиной индуктивного сопротив-

ления, но несомненно, что это сопротивление и ЭДС прямо пропорциональны, так как ЭДС

прямо пропорциональна произведению величины тока и индуктивного сопротивления. Ин-

дуктивное же сопротивление для линейных элементов не зависит от величины тока.

Индуктивное сопротивление обозначается буквой

X , а на чертеже знаком

Емкостное сопро2.1.5. тивление

Емкость влияет также на величину тока в цепи, следовательно, она проявляет себя

как н ного тока (рассматриваем только установив-екоторое сопротивление. Для постоян

шийс о большим сопротивлением. Это означает я процесс) емкость обладает бесконечн

разрыв в цепи, так как тока в такой цепи не будет.

Емкость, включенная в цепь переменного тока, уменьшает величину тока (рас-

сматриваем случай, когда в цепи нет индуктивности). Когда напряжение сети растет, то

конденсатор заряжается, накапливаемые заряды на обкладках конденсатора противодей-

ствуют вновь подходящим зарядам (одноименные заряды отталкиваются) и ток в цепи

уменьшается. При уменьшении напряжения источника конденсатор разряжается – и

этим поддерживает ток в цепи. Следовательно, конденсатор противодействует измене-

нию тока, т. е. он противодействует прохождению переменного тока, а это мы и воспри-

нимаем как определенное сопротивление. Сопротивление конденсатора называется ем-

костным сопротивлением и обозначается буквой

X , а на схеме знаком --||--.

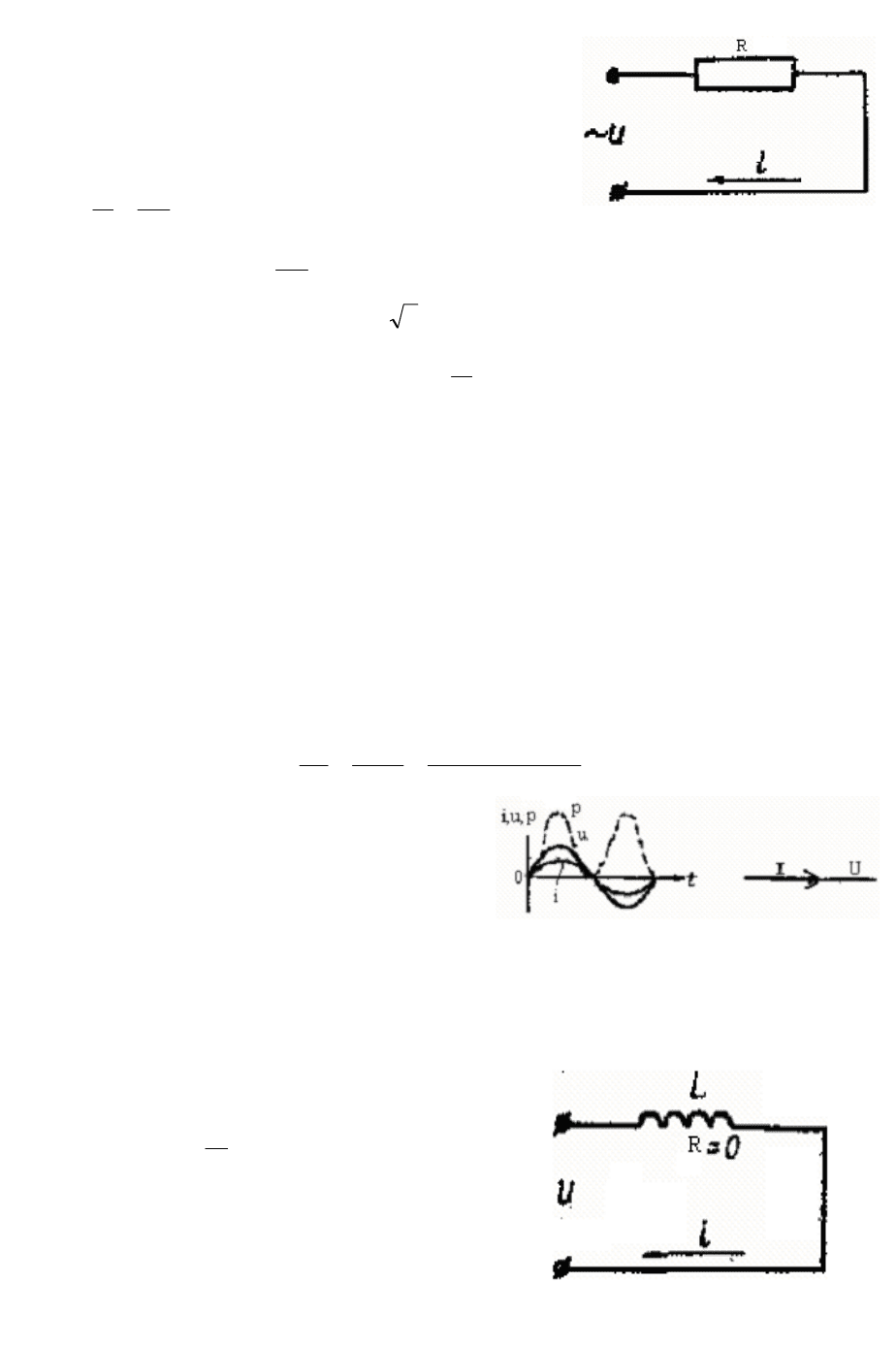
2.1.6. Цепь переменного тока только с активным сопротивлением

В данной цепи отсутствуют индуктивность и

емкос

ть, а имеется только активное сопротивление,

преобразующее электрическую энергию в другой вид

энергии (рис. 2.8).

При напряжении источника

tUu

sin

ток в

цепи

tIt

ω=ω== sinsin

совпадает по фазе с

Рис. 2.8

является амплитнапряжением. Здесь удой

тока а. Р зделив обе части равенства на 2 , получим

I =

т. е. ений тока и напряжения формула закона Ома для этой цепи и действующих знач

имее такой же вид, как и для постоянного тока. т

Мгновенная мощность в цепи только с активным сопротивлением всегда положительна:

tPtUItUtIP

mmmmm

ω=ω=ω⋅ω= sinsinsinsin .

Это означает, что электрическая энергия всегда направляется от источника к по-

требителю, где и преобразуется в другие виды энергии. Средняя мощность Р – отноше-

ние энергии, израсходованной за период (

A ), к продолжительности периода – равна

произведению действующего значения тока на действующее значение напряжения:

tdtIUpdt

===

∫∫

sin

TTT

На с. 2.9 показаны графики напряже-ри

ния, и мощности этой цепи, а также век-тока

торная диаграмма тока и напряжения.

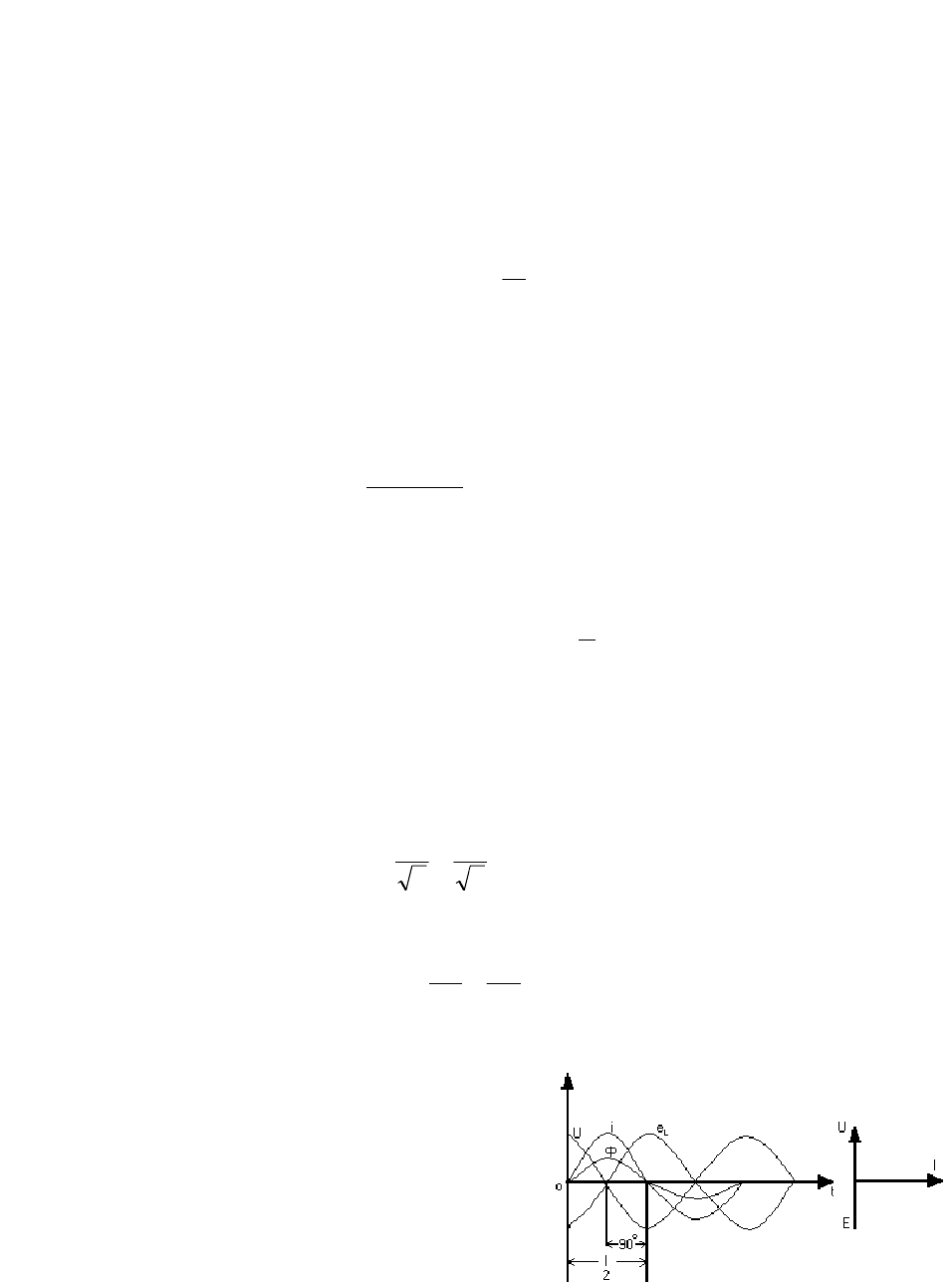
2.1.7. Цепь переменного тока только с индуктивностью

Рис. 2.9

При прохождении по такой цепи тока

tIi

ω= sin

(рис. 2.10) в цепи возникает ЭДС са-

моиндукции

Le −=

, прямо пропорциональная

скорости изменения тока.

При синусоидальном изменении тока (рис.

2.11) наибольшая скорость его будет в момент

прохождения тока через нулевые значения, и ЭДС

в эти моменты будет наибольшая. При наиболь-

шем значении тока скорость его изменения авна нулю, и ЭДС в эти моменты време-

Рис. 2.10

I р

ни тоже будет равна нулю. Согласно правилу ЭДС самоиндукции препятствует Ленца

всяко а всегда дейст-му изменению тока, благодаря чему в моменты нарастания тока он

вует австречу току (ток и ЭДС будут иметь разные знаки). В моменты убывания тока н

ЭДС ДС будут иметь одинаковые действует в том же направлении, что и ток (ток и Э

знаки). Согласно второму закону Кирхгофа для рассматриваемой цепи будем иметь

iReu

Тогда

Leu

=−= .

Поскольку

tIi

sin

то

tLI

ωω=

tdI

= cos

sin

При =ωt напряжение будет максимал1cos ьным, т. е.

LIUu

, и значение

напряжения в любой момент времени можно записать так:

sin(cos

+ω=ω= tUtUu

Другими словами, в чисто индуктивной цепи напряжение опережает ток на чет-

верть периода, а ЭДС будет противоположна по фазе напряжению и будет отставать по

фазе от тока на четверть периода. Так как

LIU

ω=

то

I =

fLLX

π=ω

2 при этом величина называется индуктивным сопротивлением.

Рис. 2.11