Курахтина Г.С. Общая электротехника: Учебное пособие

Подождите немного. Документ загружается.

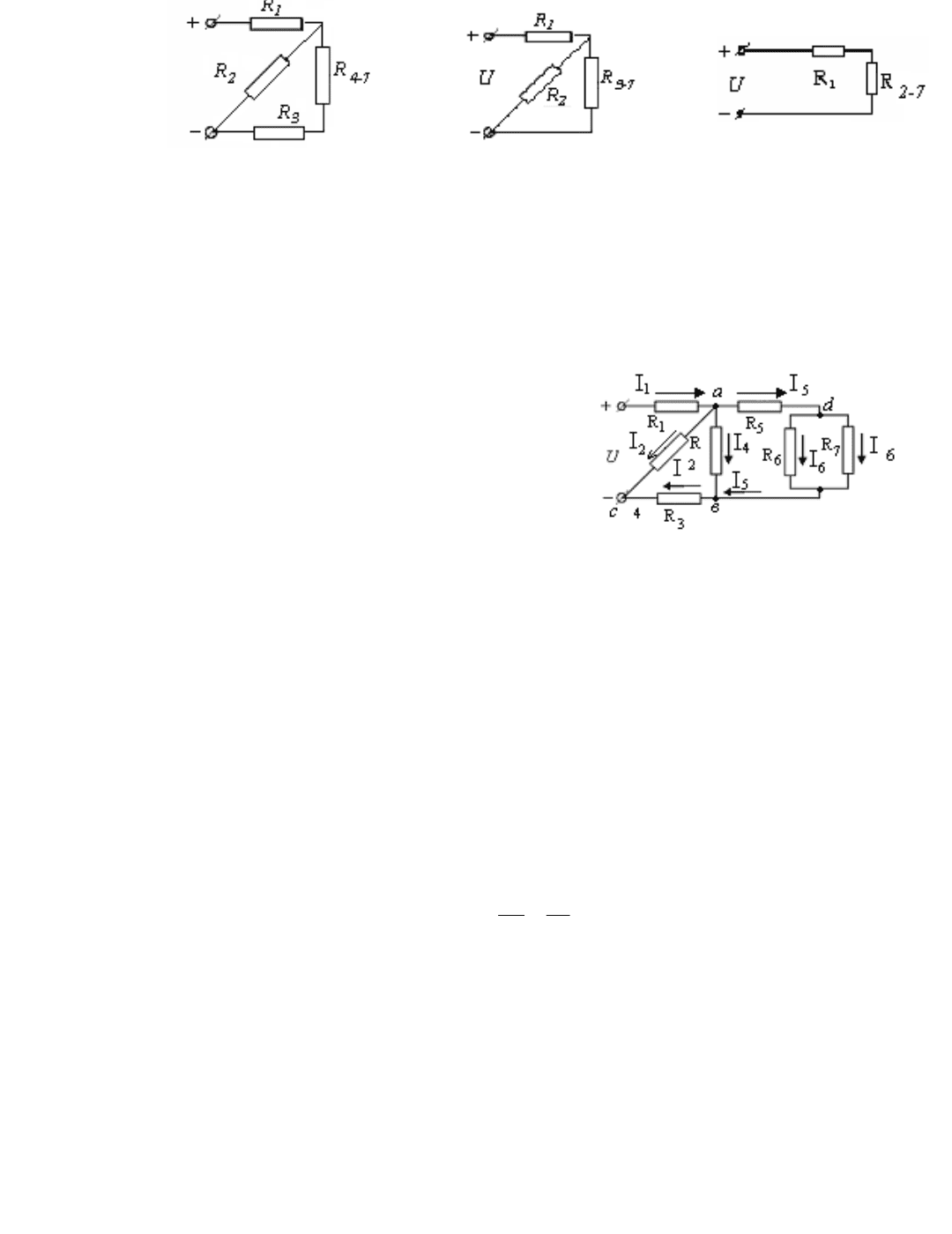
Рис. 1.35 Рис. 1.36 ис. 1.37 Р

На этом заканчивается первый этап решения задачи.

Второй этап

Вернемся к схеме (рис. 1.31) и для удобства вычертим ее еще раз (рис. 1.38). При

питании от одного источника энергии легко указать направления токов в каждом сопро-

тивлении (рис. 1.38).

Мы нашли общий ток, который является

током, проходящим через первое сопротив-

ление вл н я

. Зная величину этого сопроти е и ,

можно найти напряжение, теряемое на пер-

вом сопротивлении:

В.3666

111

= RIU =⋅=

Напряжение на втором сопротивлении

Рис. 1.3

меньше напряжения источника на величи-

ну падения напряжения на первом сопротив-

лении U

, так как напряжение источника всегда равно сумме падений напряжений на со-

противлениях внешнего участка цепи, по которым мы перемещаемся по ходу тока от од-

ной клеммы источника (плюс) до другой клеммы (минус), зависимо от того, по каким не

путям тока мы при этом перемещаемся. Это значит, что напряжение источника в нашем

случа ротивлении плюс напряжение на вто-е равно, во-первых, напряжению на первом соп

ром сопротивлении; во-вторых, сумме падений напряжений на первом, четвертом и треть-

ем сопротивлениях; в-третьих, сумме падений напряжений на первом, пятом, шестом

(или седьмом) и третьем сопротивлениях. На основании изложенного можно написать:

В8436120

−

UUU

Поскольку величина второго сопротивления задана и напря иложенное к жение, пр

нему, найдено, то по закону Ома можно найти ток во втором сопротивлении:

А2

===

Нам известен ток источника, а этот ток, в соответствии с первым законом К рхги о-

фа, для точки с равен сумме второго и третьего токов:

III

В этом равенстве неизвестен ток третьего сопротивления оторый определяется так: , к

А426

−

III

Величина третьего сопротивления задана, а ток в нем найден. Следовательно, на-

пряжение на этом сопротивлении легко подсчитать:

В3694

333

⋅

RIU

Напряжение на четвертом сопротивлении U

меньше напряжения второго сопро-

тивления на величину напряжения, приложенного к третьему сопротивлению. Следова-

тельно,

= U

– U

= 84 – 36 = 48 В.

Другими словами, напряжение четвертого сопротивления меньше напряжения ис-

точника н у напряжения первог его сопротивлений: а величин о и треть

В48)3636(120)(

314

−

+−= UUUU

По закону Ома находим ток четвертого сопротивления:

I 1

===

Применим первый закон Кирхгофа для точки а или в. Для точки а

5421

IIII

для точки в

543

III

В каждом из этих уравнений ам неизвестен ток пятого сопротивления, следова-н

тельно, найдем его следующим образом:

А314илиА,3)12(6)(

4115 435

−=+−= IIII

−

III

Используя закон Ома, найдем падение напряжения на пятом : сопротивлении

В.1863

555

⋅

RIU

Напряжение на шестом и седьмом сопротивлениях меньше напряжения на четвер-

том сопротивлении на величину падения напряжения на пятом сопротивлении согласно

свойствам параллельного и последовательного соединения сопротивлений. Тогда

В,301848

5476

−

== UUUU

или

В.30)1836(120)(

3516

−

+−

UUUUU

Решение задач первого типа не вызывает трудностей, какой бы сложной ни каза-

лась предложенная схема. Применяя рассмотренный прием решения, можно найти без

особых трудностей необходимые величины.

1.2.34. Второй тип задачи

Задачи второго типа, в которых неизвестно

или напряжение источника, или какое-либо сопро-

тивление внутри схемы, являются задачами более

трудными в том смысле, что нельзя заранее указать

путь их решения для любого условия, основываясь

только на тех приемах решения, которые рассмот-

рены выше.

Рассмотрим задачу второго типа.

Рис. 1.39

Для примера возьмем схему, приведенную на рис .39. . 1

Даны: R = 5 Ом; R = 159 Ом; R = 30 Ом; R = 24 Ома; R = 16 Ом; R = 12 Ом;

1 2 3 4 5 6

I = 2

А. Найти напряжение источника.

Зная ток четвертого сопротивления и величину этого сопротивления, найдем по за-

кону напряжение на четвОма ертом сопротивлении:

В48242

444

⋅

RIU

Сопротивления пятое и шестое по отношению к четвертому сопротивлению соеди-

нены параллельно. Следовательно, напряжение на каждом из ни ставит 48 В. х со

Это позволяет найти токи в пятом и шестом сопротивлениях:

.А3

4848

;А4

======

По первому закону Кирхгофа ток в третьем сопротивлении равен сумме токов чет-

вертого, пятого и шестого сопротивлений. Следовательно,

А9432

6543

= IIII

По закону Ома можно найти падение напряжения на третьем сопротивлении:

.В270309

333

⋅

RIU

Второе сопротивление по отношению к сопротивлениям третьему и четвертому,

пятому и шестому соединено параллельно. Следовательно, напряжение на втором со-

противлении равно сумме напряжении на третьем и четвертом сопротивлениях:

.В31848270

= UUU

Дальше найдем ток второго сопротивления:

.А2

159

318

===

По первому закону Кирхгофа ток первого сопротивления равен сумме токов второ-

го и третьего сопротивлений:

.А1192

321

III

Найдем напряжение на первом сопротивлении:

.В55511

111

⋅

RIU

Напряжение источника равно сумме напряжений на первом и втором сопротивле-

ниях или сумме напряжений на первом, втором и четвертом (пятом или шестом) сопро-

тивлениях. Следовательно,

,В37331855

= UUU

или

.В3734827055

431

+= UUUU

1.2.35. Анализ электрической схемы

Мы изучаем законы и свойства электрических цепей при ом соединении различн

потре изе процессов, происходя-бителей для того, чтобы эти знания применять при анал

щих в электрических цепях. Можно знать формулировку закона, можно перечислить

свойства цепи при том или ином способе соединения потребителей. Но если не пони-

мать процессов, происходящих в цепях при изменении каких-либо параметров, то мож-

но считать, что законы не усвоены и свойства схемы не поняты. Проверить, насколько

усвоены законы постоянного тока и свойства цепи при азличном соединении потреби- р

телей, очень легко.

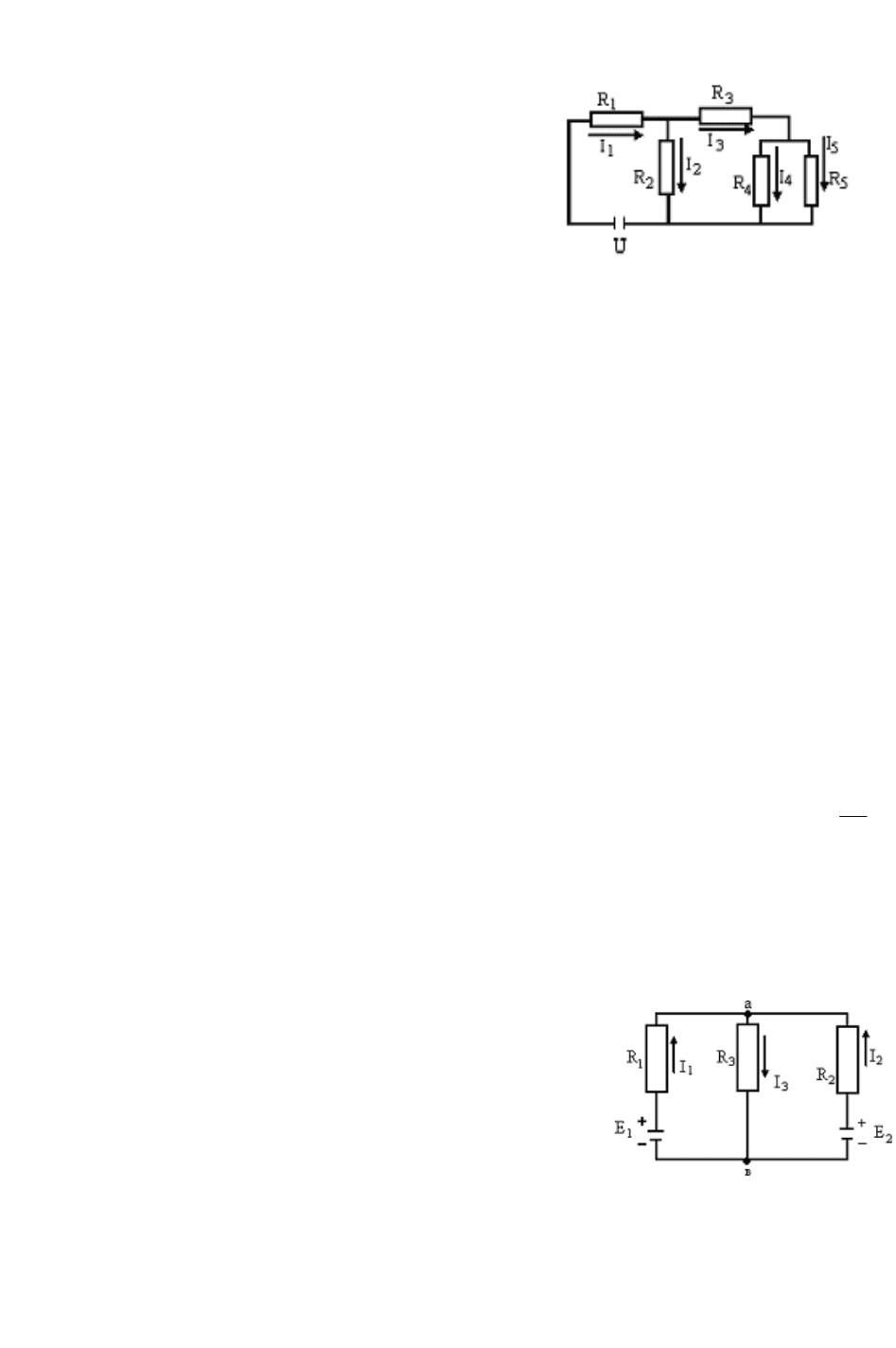
На рис. 1.40 изображена электрическая схема с

пятью сопротивлениями. Если студент (курсант)

правильно объясняет, что происходит с токами в ка-

ждом сопротивлении при уменьшении или увеличе-

нии одного (любого) из этих сопротивлений, не про-

изводя никаких расчетов, то можно смело считать,

что этот студент (курсант) хорошо знает законы по-

стоянного тока. Разумеется, это объяснение он дол-

жен давать для любой схемы, а не только для изобра-

Рис. 1.40

женной на рис. 1.40. На примере данной схемы

покажем, как целесообразнее всего проводить подобный анализ.

Требуется объяснить, как изменятся токи в каждом , если сопротив- сопротивлении

ление R

уменьшить, а напряжение источника U остается неизменным.

Если уменьшается одно из сопротивлений схемы, то и общее сопротивление в цепи

уменьшается. Соответственно при увеличении любого из сопротивлений схемы общее

сопротивление цепи увеличивается. В данном случае при уменьшении сопротивления R

общее сопротивление цепи уменьшается, в результате чег общий ток (это будет ток о

) увеличится. Увеличенпервого сопротивления ие тока вызывает увеличение на-

пряжения на первом сопротивлении (

111 2

RIU

) и и U

3,4,5

, уменьшение напряжений

так как U

= U – U

Уменьшение напряжения U

будет сопровождаться уменьшением тока

. Ток

увеличится, поскольку

213

III −=

. В результате увеличения тока I

напряжение U

= I

увеличится, а напряжение U

= U

уменьшится, так как U

= U

– U

. При этом U

уменьшилось, a U

возросло. Можно рассуждать и так:

= U – (U

+ U

U, по условию, осталось неизменным, a U

увеличились. В результате Но и

можно сделать такой вывод: напряжения U

и U

уменьшились, тем самым ток

I =

уменьшился, так как R

не изменилось. Ток

534

III

−

увеличился, поскольку I увели-

чился I

уменьшился.

1.2.36. Второй закон Кирхгофа

, a

Этот закон обычно применяется при расчете элек-

трических цепей с несколькими источниками питания.

Для цепи, изображенной на рис. 1.41, напряжение

межд точками а и в может быть выражено следующими у

уравнениями:

33222111

,, RIURIEURIEU

ававав

−=−=

Из этих уравнений видно, что правые части их рав-

ны между собою, т. е.

Рис. 1.41

222112111

RIERIERIE

−

(1)

откуда

221121

IRIEE R

−

Соответственно будем иметь:

33111

RIRIE

33111

E RIRI

(2)

233222

ERIRIE

3322

RIRI

−

(3)

Уравнения 1–3 выражают второй закон Кирхгофа, который читается так: во всяком

замкнутом контуре электрической цепи алгебраическая сумма алгебраиче- ЭДС равна

ской сумме падений напряжений на сопротивлениях, входящи контур. При со-х в этот

ставлении уравнений по второму закону Кирхгофа обходят выбранный контур в произ-

вольном направлении. ЭДС и падения напряжения считаются положительными

(ставятся в уравнение со знаком +), если направления ЭДС и соответствующих токов

совпадают с направлением обхода контура; ЭДС и падения напряжения считаются отри-

цательными, если направления ЭДС и токов в соответствующих сопротивлениях проти-

воположны направлению обхода контура. Любую сложную схему с каким угодно чис-

лом источников питания можно рассчитать, применяя законы Кирхгофа. При решении

подобных задач произвольно задают направления токов в ветвях и составляют столько

уравнений, сколько имеется неизвестных величин (токов, сопротивлений или ЭДС),

применяя первый закон Кирхгофа для отдельных точек разветвления и второй закон

Кирхгофа для отдельных внутренних ко . нтуров

Ветвь – это участок цепи, заключенный между двумя точками разветвления, вдоль

котор но е-ого ток имеет одно и то же значение. Ветвь может включать в себя од или н

сколько последовательно енных сопротивлений с источником энергии или без соедин

такового, а также может состоять только из источника энергии без сопротивлений.

Составленные уравнения должны быть независимыми друг от друга: одно из них

не должно быть следствием других. Поэтому если цепь имеет n точек разветвления, то

по первому закону Кирхгофа соста уравнений. вляется лишь (n – 1)

Недостающие уравнения составляются по второму закону Кирхгофа. При этом на-

до следить за тем, чтобы в контур, для которого составляется уравнение, входила хотя

бы одна новая ветвь, еще не входившая ни в один из ранее рассмотренных контуров.

Если при решении получается отрицательное значение тока в какой-либо ветви,

то это указывает на то, что ток в этой ветви правление, обратное тому, каким имеет на

мы задались.

В качестве примера рассмотрим схему на

рис. 1.42. В данном случае мы имеем две точки

разве з трех вет-твления: в и c. Схема состоит и

вей, ждая из которых заключена между точ-ка

ками c и в.

Первая ветвь включает в себя сопротивление

, источник E

и сопротивление R

, по которым

проходит один и тот же ток. Обозначим его как I

и будем считать, что ток идет по направлению ча-

совой стрелки.

Рис. 1.42

Вторая ветвь включает в себя одно сопро-

тивление R

. Ток, идущий по нему, обозна через I

чим

и будем считать, что он идет слева направо.

ретья ветвь включает сопротивление R и источник E . Будем считать, чтоТ

2 2

ток по

этой ветви идет справа налево, и обозначим его через I

В схеме имеются три ветви, следовательно, имеются три различных тока: I

, I

которые и надо определить.

Раз мы имеем две точки разветвления (п = 2), , по первому закону следовательно

Кирх уравнение (n – 1) для точек разветвления в или c. гофа мы можем написать одно

Напишем это уравнение для точки в:

231

III

По второму закону Кирхгофа мы можем написать три уравнения, так как имеем

три контура: первый – afвca , второй – afвkвca, третий – вkdcв.

Но нам требуется (и мы можем написать) только два независимых уравнения согласно

второму закону Кирхгофа. Напишем эти уравнения для первого и третьего контуров.

Обходя первый и третий контуры по часовой стрелке, приписывая токам и ЭДС

знаки плюс, когда их направления совпадают с направлением обхода, и знаки минус, ко-

гда их направления противоположны направлению обхода, получим два уравнения:

для первого контура:

;)(

113431

RIRRIE

−

для третьего контура:

22112

RIRIE

Решая совместно ранее полученное уравнение по первому закону Кирхгофа и эти

два уравнения, найдем токи

321

,, III

. Всегда следует проверять правильность решения

составленных уравнений подстановкой полученных значений

321

,, III

в каждое на-

чальное уравнение.

Практические задания

1. По какой формуле подсчитывается сила взаимодействия электрических зарядов:

)3;

)2;

RRR

ааа

πεπεπε

2. На одной из вершин равносторон-

него треугольника находится заряд Q. На-

пряженность электрического поля в цен-

тре треугольника вна 4 В м. Чему равна ра /

напряженность поля в центре треугольни-

ка, если:

а) на двух других вершинах треуголь-

ника будут находиться электрические заря-

ды того же знака и той же величины?

б) на двух других вершинах будут на-

ходиться заряды такой же величины, но

противоположного знака с зарядом

3. Какие величины вычисляются по этим формулам:

.)4;

)3;

)2;

ааа

πεπεπε

4. Электрическое поле заряда Q имее

в точке в потенциал, равный 4 В. Чему бу-

дет равен потенциал в точке в, если:

а) в точку с поместить заряд, равный

заряду Q и того жe знака;

б) в точку с поместить заряд, равный

заряду

Q, но противоположного знака.

5. В одной из вершин квадрата находит-

ся за

ряд Q, при этом потенциал электриче-

ского поля в центре квадрата равен 10 В. Че-

му равен потенциал в центре квадрата, если

во всех вершинах его будут находиться заря-

ды одного знака и одинаковой величины?

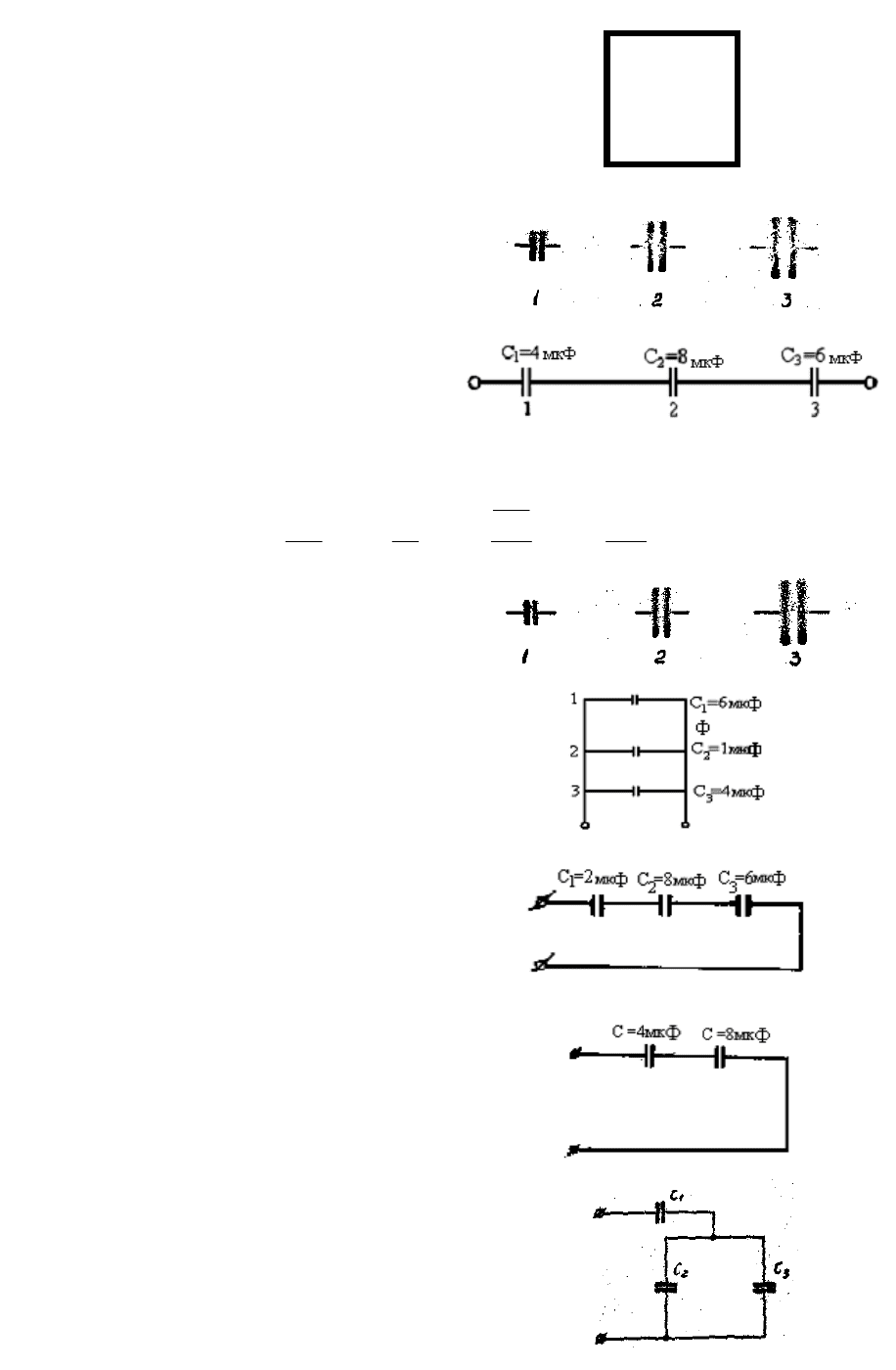
6. Какой конденсатор накопит наи-

больший заряд при одинаковом напряжении

на н ских размерах,их и при геометриче

пропорциональных чертежу?

7. На каком конденсаторе будет наи-

большее напряжение?

8. Какие величины вычисляются по этим формулам:

.)4;)3;)2;)1

аа

2dd l

9. Какой конденсатор имеет наиболь-

шую емкость, если геометрические размеры

пропорциональны чертежу?

10. На каком конденсаторе будет

больше накоплено энергии?

11. Напряжение на третьем конденса-

торе равно 40 В. Чему равны напряжения на

остальных конденсаторах и общее напря-

жение?

12. Электрическое поле второго кон-

денсатора

обладает энергией в 100 Дж.

Какой энергией обладает электрическое по-

е первого конденсатора

С ?

13. Конденсаторы, соединенные по

схеме, имеют одинаковую ем-

кость. Напряжение на вто

указанной

ром конденсаторе

составляет 60 В. Какое напряжение на пер-

вом конденсаторе?

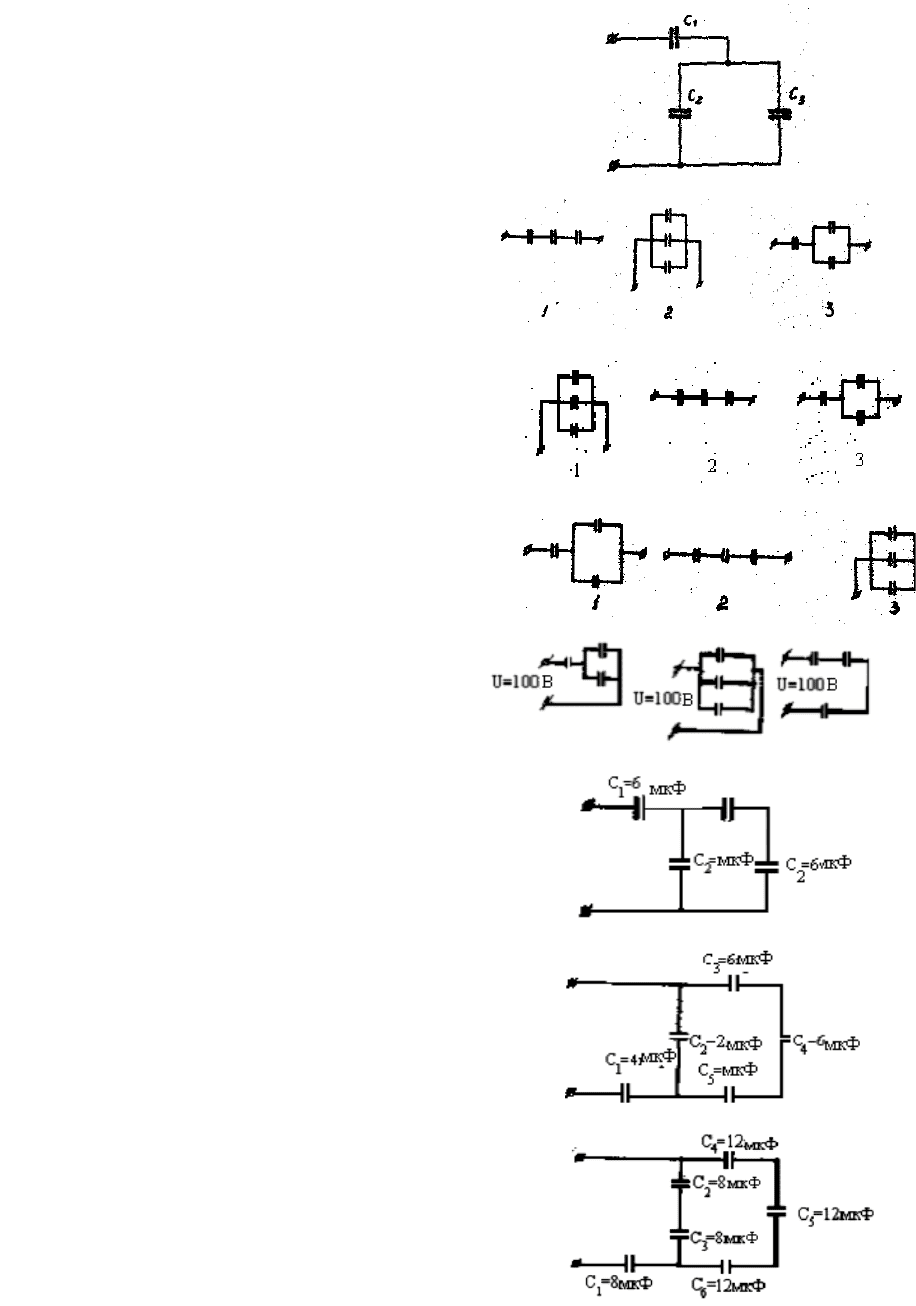
14. Конденсаторы, соединенные по

указанной схеме, имеют одинаковую ем-

кость. Заряд на первом конденсаторе

ра-

ен 12 мкК. Какой заряд на третьем кон-

денсаторе?

15. Батареи собраны на одинаковых

конденсаторах. Какая из них накопит наи-

больший заряд при одинаковом напряжении

на батареях?

16. Батареи собраны из одинаковых

конденсаторов. Какую из них можно под-

ключить

под наибольшее напряжение?

17. Батареи собраны из одинаковых

конденсаторов. Какая из них имеет наи-

большую емкость?

ско

наков

18. Какая из батарей конденсаторов

обладает наибольшим запасом электриче-

й энергии? (Конденсаторы имеют оди-

ую емкость.)

по ука-

зан

С = 6 мкФ,

19. Конденсаторы соединены

ной схеме, при этом

= С =

2 4

= 3 мкФ. Чему равна общая емкость

батареи?

20. Конденсаторы соединены по указан-

ной схеме. При этом С

= 4 мкФ, C

= 2 мкФ,

= 4 мкФ, С

= 6 мкФ, С

= 6 мкФ. Заряд

на пятом конденсаторе равен 5 мкК. Чему

авняется заряд всей батареи?

21. Конденсаторы с единены по ка-о у

занной схеме. Заряд на шестом конденсато-

е равен 20 мкК. Чему равно напряжение

источника?

22. Конденсаторы соединены по указан-

ной схеме. При этом C

= C

= 4 мкФ,

а С

= С

= 2 мкФ. Напряжение на пятом

конденсаторе (U

) равно 50 В. Чему равно

напряжение источника?

23. Известно, что С

= 4 кФ, С

= 8 мкФ,

= 8 мкФ. Что произойдет с величиной

заряда на втором конденсаторе, если кон-

денсаторы

и С местами?

Ответ: 1)

поменять

увеличится;

2) уменьшится;

3) не изменится.

мкФ,

= 6 мкФ.

Что произойдет с напряжением на чет-

вертом конденсаторе, если конденсаторы

и С

ьшится;

3) не изменится.

24. Известно, что

= 12 мкФ, С

= 12

поменять местами ?

Ответ: 1) увеличится;

2) умен

м формулам: 25. Какие величины вычисляются по эти

.)4;)3;

м формулам:

)2;)1

26. Какие величины вычисляются по эти

.)4;)3;)2;

It γ

27. Какие величины вычисляются по этим формулам:

PQU

.)4;

)(

)

сляются по этим формулам:

3;)2;)1

UQUI

28. Какие величины вычи

.)4;

)(

REU

γ+

;)2;)1

RtI

29. Лампы рассчитаны на одно на-

пряжение. Какая

из них будет давать

боль света?

ше

30. Что произойдет с общим током це-

пи, если увеличить сопротивление R

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

31. На каком из трех сопротивлений

выделяется наибольшее количество энергии?

Ответ: 1) на сопротивлении

;

2) на сопротивлении

;

ении

R . 3) на сопротивл

32. Лам на одинаковыепы рассчитаны

напряжения. будет даватьКакая из них

больше света?

Ответ: 1) лампа № 1;

2) лампа № 2;

3) лампа № 3.

33. Что произойдет с током

, если

в потреби-

теле

ебитель R

Ответ:

отключить потр

1) увеличится;

2) уменьшится;

3) не изменится.

34. Что произойдет с нагрузкой на ге-

нера

2) уменьшится;

3) не изменится.

торе, если увеличить сопротивление R

Ответ: 1) увеличится;

35. На изображенной на рисунке схеме

поменяли местами сопротивления R

и R

то с

2) уменьшится;

тало с током в цепи?

: 1) увеличится; Ответ

3) не изменится.

36. Что произойдет с напряжением н

сопротивлении R

, если уменьшить величи-

ну сопротивления R

Ответ: 1) увеличится;

2) уменьшится;

3) не изменится.

37. Чт произойдет с нагрузкой на ге-о

нератор, если сопротивление R

ум

твет: 1) увеличится;

2) уменьшится;

еньшить?

3) не изменится.