Куцый Н.Н. Теория оптимального управления
Подождите немного. Документ загружается.


Решение изопериметрической задачи методом множителей Лагранжа проиллю-
стрируем на следующем примере. Требуется найти кривую заданной длины
l
, кото-
рая соединяет точки
A
и
B
и которая ограничивает совместно с отрезком
AB
наи-
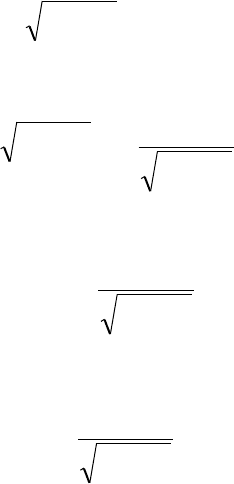
большую площадь (рис. 12.1). Выберем систему прямоугольных координат таким об-
разом, чтобы ось абсцисс проходила через точки
A
и
B
. Тогда площадь, ограничен-
ная искомой кривой
)(xy
, определяется функционалом
dxyI
b
a
∫
=
2512 ).(
.
Необходимо найти функцию
)(xy
, доставляющую максимум функционалу
(12.25) при условии
ldxyI
b
a
=
′
+=
∫
2
1
и
0
==
)()( byay
.
Будем считать, что
abl
−>
.
Введём множитель Лагранжа
λ
и составим новый функционал
(
)
dxyyI
b
a
∫
′
++=
2
1 2612
λ
*
).(
.
Первый интеграл уравнения Эйлера-Лагранжа для функционала (12.26) имеет
вид
1
2712 CFyF
y
=
′
−
′
).(
,
где
61
A
B
λ
x
y
0
Рис. 12.1
2
1 yyF
′
++=
λ
;
−
1
C
постоянная интегрирования.
Из (12.27) следует
1
2
2
2
1
1 C
y
y
yy
=
′
+
′
−
′
++
λλ
,
откуда
2
1
1
2812
y
Cy
′
+
−=
λ
).(
.
Уравнение (12.28) представим в виде
( )
2
2
2
1
1 y
Cy
′
+
=−
λ
.
Интегрирование последнего уравнения даёт в качестве решения уравнение
окружности радиуса
λ
( ) ( )
2
2
1
2
2
λ
=−+−
CyCx
.
Постоянные
21
CC ,
и множитель Лагранжа
λ
определяются из условий прохо-
ждения окружности через точки
BA,
и из условия равенства
l
длины окружности
между
A
и
B
. Наибольшая площадь ограничивается прямой
AB
и частью окружно-
сти радиуса
λ
, проходящей через точки
A
и
B
.
62

13.МЕТОДЫ РЕШЕНИЯ. ПРИНЦИП МАКСИМУМА
Принцип максимума применим к системам или объектам, поведение которых
можно описать системой дифференциальных уравнений
=
=
=
),,,,;,,,(
),,,,;,,,(
),,,,;,,,(
).(
rn
n
rn
rn
uuuxxxf
dt
dx
uuuxxxf
dt
dx
uuuxxxf
dt
dx
21211
21212
2
21211
1
113
где
−
i
x
координаты объекта;
−
j
u
управления.
Управление движением объекта характеризуется точками
),,,(
r
uuuu
21
=
не-
которой
−
r
мерной области управления
U
.
В физических системах или объектах управлением некоторые физические пара-
метры, например температура, количество топлива и т.д., на которые накладываются
ограничения вида
1 213
≤
j
u).(
.
Функции
i
f
непрерывны по совокупности всех аргументов и непрерывно диф-
ференцируемы по совокупности фазовых координат
n
xxx ,,,
21
.
Если выбрать ограниченные, кусочно-непрерывные, с разрывами первого рода
функции управления
)(,),(),( tututu
r
21
, то при заданных начальных условиях си-
стема дифференциальных уравнений (13.1) имеет единственное решение.
В фазовом пространстве
X
н
x
, образованном векторами
),,,(
n
xxx
21
, заданы
две точки
н
x
и
к
x
. Требуется среди допустимых управлений
)(tuu
=
, которые пере-
водят точку из начального положения
н
x
в конечное
к
x
, найти такое управление, для
которого функционал
∫
=
к
0
21210
313
t
t
rn
dttutututxtxtxfu I ))(,),(),();(,),(),(()().(
принимает наименьшее возможное значение. Можно показать, что в случае отсут-
ствия ограничений на управления вида (13.2) поставленная задача является частным
случаем задачи Майера.
Действительно, если ввести дополнительную функцию
)(tx
0
так, что

0 413
000
0
==
)(),,().( txuxf
dt
dx
,
и расширить систему дифференциальных уравнений (13.2) за счёт уравнения
(13.4), то получим векторное уравнение связи
),().( uxf
dt
dx
i
i
=
513
),,,,( ni
210
=
.
Функционал (13.3) с учётом (13.4) можно записать в виде
)(),()(
к00
к
0
txdtuxfuI
t
t
==
∫
.
Вариационная задача Майера формулируется как задача о нахождении управле-
ния
)(tu
, при котором решение системы уравнений связи (13.5) при условиях на кон-
цах
00
ii
xtx
=
)(
,
))(( ni 10
=
даёт наименьшее значение на правом конце
)(
к0
tx
.
Существенным отличием задачи оптимального управления от классических ва-
риационных задач является наличие ограничений вида (13.2), которые не позволяют
применять необходимые условия классического вариационного исчисления.
Принцип максимума Понтрягина, который рассматривается ниже, позволяет ре-
шать задачи оптимального управления также и в случае ограничений вида
1
≤
i
u
.
Этот принцип формулируется следующим образом.
Пусть
[ ]
)(),( txtu
,
к0
ttt
≤≤
- некоторый процесс, который переводит объект из
начального состояния
н
x
в конечное
к
x
.
Вводится в рассмотрение функция
H
, которая зависит от переменных
rn
uuuxxx ,,,,,,,
2121
и некоторых вспомогательных переменных
n
ψψψ
,,,
21
:
∑
=
=
n
i
ii
uxfux H
0
613 ),(),,().(
ψψ
.
С помощью функции
H
записывается система дифференциальных уравнений
для вспомогательных переменных
k
k
x
tutxH
dt
d
∂
∂
−=
))(),(,(
).(
ψ
ψ
713
))(( nk 10
=
.
Для оптимальности управления
)(tu
и траектории
)(tx
необходимо существова-
ние такой ненулевой непрерывной вектор-функции
))(,),(),(()( tttt
n
ψψψψ
10
=
,
64

соответствующей функциям
)(tu
и
)(tx
, что при любом
t
к0
ttt
≤≤
функция
( )
utxtH ),(),(
ψ
переменного
Uu
∈
достигает в точке
)(tuu
=
максимума и в конеч-
ный момент
к
t
выполняется условие
0 813
к0
≤
)().( t
ψ
,
( )
0
кк
=
)(),(),( tutxtH
к
ψ
.
С учётом соотношения (13.6) систему дифференциальных уравнений (13.7) мож-
но записать в виде
∑
=
∂
∂
−=
n
i
i
k
ik
x
tutxf
dt
d
0
913
ψ
ψ
))(),((
).(
))(( nk 10
=
,
которая имеет единственное решение
),,,(
n
ψψψψ
10
=
при любых начальных условиях для
k
ψ
, если выбрано управление
)(tu
и полу-
чена фазовая траектория
)(tx
с начальным условием
н0
xtx
=
)(
.
Если
)(),(),( tutxt
ψ
удовлетворяют системам (13.1) и (13.9), то функции
)(t
0
ψ
и
∑
=
=
n
i
ii
tutxftH
0
))(),(()(
ψ
переменного
t
являются постоянными и в условии (13.8) конечную точку
к
t
можно заменить любой другой.
В весьма важном для практики частном случае, когда в функционале (13.3)
1
0
=
),( uxf
, имеем задачу об оптимальном быстродействии. Согласно принципу мак-
симума для оптимальных по быстродействию процессов необходимо существование
такой ненулевой непрерывной вектор-функции
))(,)(),(()( tttt
n
ψψψψ
21
=
,
соответствующей функциям
)(tu
и
)(tx
, что для всех
t
)(
к0
ttt
≤≤
функции
∑
=
=
n
i
ii
uxfuxH
0
(13.10) ),(),,(
ψψ
переменного
Uu
∈
достигает максимума в точке
)(tuu
=
и в конечный момент
к
t
выполняется условие
0 (13.11)
ккк
≥
))(),(),(( tutxtH
ψ
.
Если величины
)(),(),( tutxt
ψ
удовлетворяют системе
65

i
i
H
dt
dx
ψ
∂
∂
=
,
i
i
x
H
dt
d
∂
∂
−=
ψ
))(( ni 11
=
и выполнено условие максимума, то функция
))(),(),(( tutxtH
ψ
переменного
t
постоянна и условие (13.11) можно проверять при любом значении
t
)(
к0
ttt
≤≤
.
В случаях, когда и функционалы, и уравнения связи линейны как относительно
управления, так и относительно фазовых координат или линейны только относитель-
но управления, например имеют вид
),,(),,
nini
i
xxuhxxg
dt
dx
11
( (13.12)
+=
,
ni )(11
=
,
где функции
i
g
и
i
h
могут быть нелинейными, принцип максимума позволяет
по одному функции
H
найти функции, на которых функция
H
достигает максиму-
ма.
Если уравнения движения объекта имеют вид (13.12) и ставится задача о макси-
мальном быстродействии, то согласно (13.10) функция
H
запишется в форме
∑
=
+=
n
i
iii
uhgH
1
)(
ψ
,
и при наличии ограничения вида
1
≤
u
можно сделать вывод, что максимум
функции
H
достигается на функции
∑
=
=
n
i
ii
hsignu
1
ψ
.
В этих случаях принцип максимума позволяет достаточно эффективно решать
задачи оптимального управления.
В общем случае, когда функционалы или уравнения связи нелинейны по управ-
лению, применение принципа максимума встречает определенные трудности, так как
принцип максимума позовляет установить, что экстремум функционала достигается
на кривой, составленной из отрезков экстремалей и отрезков границы области
1
±=
u
,
а условия в точках сопряжения этих отрезков более сложные. чем в вариационном ис-
числении.
К недостаткам принципа максимума можно отнести требование задания динами-
ки движения объекта или процесса в виде системы дифференциальных уравнений
(13.1), т.е.
66
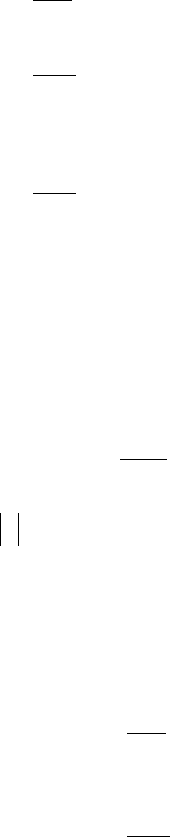
=
=
=
),,,,;,,,(
),,,,;,,,(
),,,,;,,,(
rn
n
rn
rn
uuuxxxf
dt
dx
uuuxxxf
dt
dx
uuuxxxf
dt
dx
21211
21212
2
21211
1
,
разрешенных относительно производных. В этом отношении методы классиче-
ского вариационного исчисления имеют преимущество, так как позволяют опериро-
вать с ситемами общего вида, неразрешенными относительно производных.
Рассмотрим применения приницпа максимума. пусть дивжение объекта управле-
ния описывается дифференциальным уравнением
u
dt
xd
=
2
2
(13.13)
,
где
1
≤
u
. Дифференциальным уравнением (13.13) может описываться, например,
процесс движения по горизонтальной прямой материальной точки единичной массы
под действием управляющей силы
u
без учёта сил сопротивления.
Уравнения движния (13.13) представим в виде системы дифференциальных
уравнений
=
=
.
,
).(
u
dt
dx
x
dt
dx
2
2
1
1413
С помощью принципа максимума решим задачу о быстрейшем попадании мате-
риальной точки в начало координат (0,0) из заданного начального состояния
),(
2010
xx
. Другими словами, необходимо найти такой закон упарвления
)(tu
, кото-
рый с максимальным быстродействием переводит материальную точку, имеющу, на-
чальную скорость
20
x
, из заданного начального положения
10
x
в начало отсчёта с ну-
левой скоростью.
Составим для системы уравнений (13.14) функцию
H
согласной соотношению
(13.6)
uxH
221
1513
ψψ
+=
).(
.
Система дифференциальных уравнений для вспомогательных переменных
1
ψ
и
2
ψ
согласно (13.7) имеет вид
67

.
,
1
2
1
0
ψ
ψ
ψ
−=
=
dt
d
dt
d
Решая систему для вспомогательных переменных, получаем
,
,
212
11
CtC
C
+−=
=
ψ
ψ
где
−
21
CC ,
постоянные интегрирования.
Рассматривая функцию
H
(13.15) согласно принципу максимума, находим, что
оптимальные управления, доставляющие максимум функции
H
, определяются соот-
ношениями
,)(,)( 0 если 1
2
>+=
ttu
ψ
).( 1613
.0)( если ,1)(
2
<−=
ttu
ψ
Это выражение для оптимального управления можно записать в виде
)()()(
212
CtCsigntsigntu
+−==
ψ
.
Следовательно, для данной задачи оптимальное управление является кусочно-
постоянной функцией, принимающей значения
1
±
и имеющей не более двух интер-
валов постоянства, так как функция
21
CtC
+−
не более одного раза меняет знак на
отрезке
к0
ttt
≤≤
.
Фазовый портрет семейства оптимальных траекторий изображён на рис. 13.1.
Если начальная точка
),(
2010
xx
расположена выше линий AOB, то фазовая точа дви-
гается под воздействием управления
1
+=
u
подуге параболы, проходящей через на-
68
2
x
1
x
A
B
0
Рис. 13.1
1
+=
u
1
−=
u
чальную точку
),(
2010
xx
, до тех пор пока она не попадёт на дугу BO. В момент попа-
дания фазовой точки на дугу BO значение управления переключается на значение
1
−=
u
и сохраняет свой значение до момента достижения начала координат.
69
14.МЕТОДЫ РЕШЕНИЯ. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Метод динамического программирования основан на принципе оптимальности,
который. Следуя Беллману, сформулируем на примере дискретного и детерминиро-
ванного процесса принятия решений.
Рассматривается некоторая физическая система, состояние которой в любой мо-
мент времени определяется вектором
p
. Комопоненты вектора
p
называются фазо-
выми переменными.
Введём в рассмотрение также семейство преобразования
{ }
qpT ,(
, где векторная
переменная
q
называется вектором решения.
На каждом шаге можно выбрать значение
i
q
из набора допустимых векторов
так, что изменяется состояние физической системы и определяющий её вектор:
),(
01
qpTp
=
,
),(
112
qpTp
=
,
. . . . . .
),(
nnn
qpTp
=
+
1
.
Процесс, состоящий из выбора
−
N
решений, называется
−
N
шаговым процес-
сом. Для оценки последовательности решений
N
qqqq ,,,,
210
и
N
pppp ,,,,
21
введём скалярную функцию
),,,,;,,,,(
NN
qqqqppppR
21021
, которая называет-
ся критерием или функцией дохода. Будем полагать, что после
K
шагов принятия ре-
шений влияние оставшихся
KN
−
шагов процесса на функцию критерия зависит
только от состояния системы в конце
−
K
го решения и от последующих решений
Nkk
qqq ,,,
21
++
.
Задача заключается в выборе такой последовательности решений, которая до-
ставляет максимальное значение функции критерия. Последовательность допустимых
решений называется стратегией (политикой). Стратегия, которая максимизирует
функцию критерия, называется оптимальной стратегией. Согласно принципу опти-
мальности Беллмана, оптимальная стратегия обладает тем свойством, что, каковы бы
ни были первоначальное состояние и первоначальное решение, последующее реше-
ние должно определять оптимальную стратегию относительно состояния, полученно-
го в результате первоначального решения.
Рассмотрим пример применения принципа оптимальности к задаче о максимиза-
ции функции дохода вида
∑
=
=
N
k
kk
qpgqqppR
0
101
),(),,,,,(
.
Максимальное значение функции дохода, которое зависит только от начального
состояния
p
и числа шагов
N
, обозначим через
)( pf
N
.
