Куцый Н.Н. Теория оптимального управления
Подождите немного. Документ загружается.


x
yy
y
ii
i
∆
−
=
+
1
,
а
)( 1
−
i
-й член
),,(
111
−−−
′
iii
yyxF
содержит
i
y
только в аргументе
x
yy
y
ii
i
∆
−
=
−
−
1
1
.
С учётом этих обстоятельств имеем
),,(),,(),,().(
111
511
−−−
′′
′
+
′
−∆
′
=
∂
∂
iiiyiiiyiiiy
i
n
yyxFyyxFxyyxF
y
I
.
Выражение (11.5) преобразуем в форму дискретного аналога уравнения Эйлера
x
x
yyxF
yyxF
y
I
iiiy
iiiy
i
n
∆
∆
′
∆
−
′
=
∂
∂
′
),,(
),,().( 611
,
где
),,(),,(
111
−−−
′′′
′
+
′
=∆
iiiyiiiyy
yyxFyyxFF
.
Принимая во внимание (11.4), т.е.
00 0
121
=
∂
∂
=
∂
∂
=
∂
∂
−
n
nnn
y
I
y
I
y
I
,,,
,
выражение (11.6) запишем в форме дискретного аналога уравнения Эйлера
0
=
∆
′
∆
−
′
′
x
yyxF
yyxF
iiiy
iiiy
),,(
),,(
.
Переходя к пределу при
∞→
n
, получаем уравнение Эйлера
0
=−
′
yy
F
dx
d
F
,
которому должна удовлетворять функция
)(xy
, доставляющая экстремум ис-
ходному функционалу (11.2). Впервые уравнение Эйлера было получено им именно
таким путём, хотя законность предельного перехода не была обоснована.
Недостаток метода Эйлера заключается в трудностях решения системы уравне-
ний (11.4), когда требуется выбрать достаточно большое количество ординат, чтобы
получить приемлемую точность вычисления. С целью демонстрации возможностей
метода Эйлера рассмотрим следующий пример.
Требуется минимизировать функционал
∫
′
++
1
0
22
2 dxyyxy )(
,
.)()( 010
==
yy
51
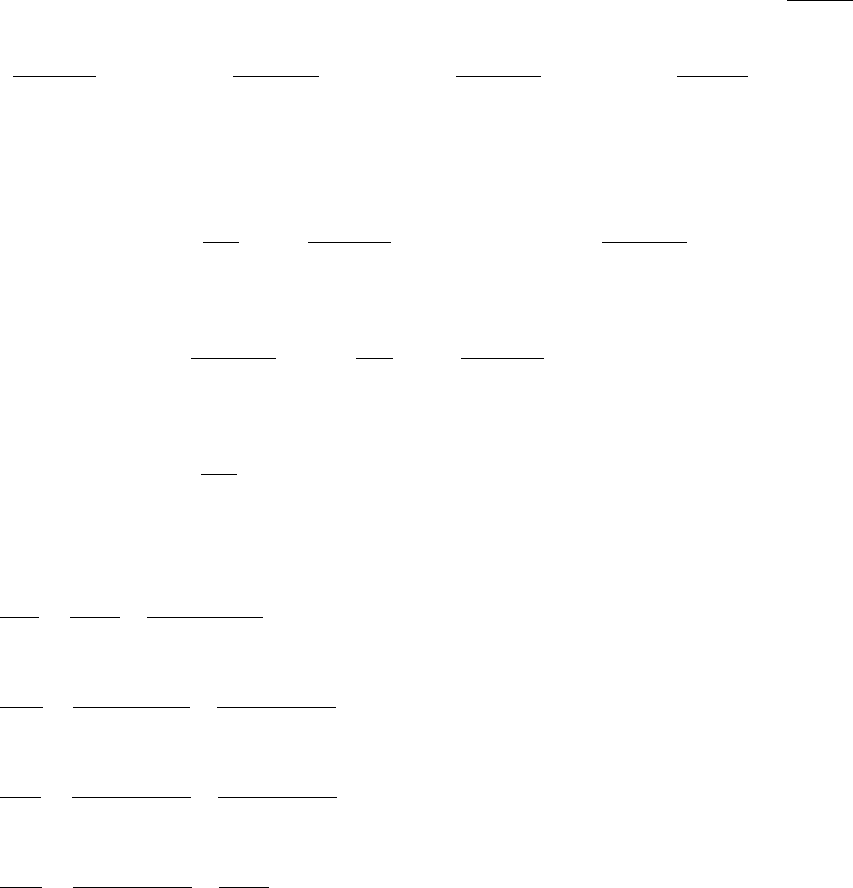
Выбираем дискретный шаг по оси абсцисс
20,
=∆
x
. Тогда имеем следующую
последовательность ординат:
00
=
)(y
,
),( 20
1
yy
=
,
),( 40
2
yy
=
,
),( 60
3
yy
=
,
),( 80
4
yy
=
,
01
5
==
)(yy
и приближённых значений производных:
20
0
0
1
,
)(
−
=
′
y
y
,
20
20
12
,
),(
yy
y
−
=
′
,
20
40
23
,
),(
yy
y
−
=
′
,
20
60
34
,
),(
yy
y
−
=
′
,
20
0
80
4
,
),(
y
y
−
=
′
. Заменяя
данный функционал суммой по формуле прямоугольников, получаем функцию
четырёх переменных
+
−
+++
−
+
=
2
23
1
2
1
2
12
2
1
4321
20
40
2020 ,
,
,,
),,,(
yy
yy
yyy
yyyyФ
+++
−
+
+
−
+++
2
2
3
2
12
2
1
2
34
2
2
2
21
202020
80 yy
yyy
yy
yy ,
,,,
,
2061
20
4
2
4
2
4
,,
,
++
+
yy
y
.
Определив частные производные и приравняв их к нулю, будем иметь
0402
040
2
040
2
1
121
1
=++
−
−=
∂
∂
,
,
)(
,
y
yyy
y
Ф
,
0802
040
2
040
2
2
23
12
2
=++
−
−
−
=
∂
∂
,
,
)(
,
)(
y
yy
yy
y
Ф
,
0212
040
2
040
2
3
3423
3
=++
−
−
−
=
∂
∂
,
,
)(
,
)(
y
yyyy
y
Ф
,
0612
040
2
040
2
4
4
34
4
=++−
−
=
∂
∂
,
,,
)(
y
y
yy
y
Ф
.
Решение данной системы линейных алгебраических уравнений с четырьмя неиз-
вестными даёт приближённые значения функции, минимизирущей функционал:
1
y
,
2
y
,
3
y
и
4
y
. С целью оценки погрешности решения приведём точные (до четвертого
десятичного знака) значения искомой функции
),( 20y
;
),( 40y
;
),( 60y
;
),( 80y
:
−=
−=
,,),(
,,
0287020
02860
1
y
y
−=
−=
,,),(
,,
0505040
05030
2
y
y
52

−=
−=
,,),(
,,
0583060
05800
3
y
y
−=
−=
.,),(
,,
0444080
04420
4
y
y
Сущность метода Ритца заключается в том, что значения функционала (11.2), т.е.
∫
′
=
2
1
x
x
dxyyxFI ),,(
axy
=
)(
1
,
bxy
=
)(
2
,
рассматриваются не на произвольных допустимых кривых вариационной задачи,
а на
−
n
параметрическом семействе функций
∑
=
+=
n
i
ii
xCxxny
1
0
711 )()(),().(
ϕϕ
,
где
−
i
C
постоянные коэффициенты;
ax
=
)(
10
ϕ
;
bx
=
)(
20
ϕ
;
0
21
==
)()( xx
ii
ϕϕ
−=
),,,,(
ni 10
последовательность линейно независимых
функций, называемых координатными функциями.
На семействе функций (11.7) исходный функционал (11.2) превращается в функ-
цию
n
переменных
),,,)),((
n
CCCxnyI
21
Ф(
=
.
Коэффициенты
n
CCC ,,,
21
выбираются из условия достижения экстремума
функции
),,,
n
CCC
21
Ф(
, т.е. определяются из системы уравнений
),,,().( ni
С
i
21 0
Ф
811
==
∂
∂
.
В случае существования предела функции (11.7) путём предельного перехода
при
∞→
n
можно получить точное решение исходной задачи. Если ограничиться
лишь
−
n
первыми членами функции (11.7), то получим приближенное решение вари-
ационной задачи.
Если методом Ритца определяется абсолютный минимуму функционала, то при-
ближенное значение функционала находится с избытком, а абсолютный максимум
функционала – с недостатком.
Решение системы уравнений (11.8) в общем случае является очень сложной зада-
чей. Выбор последовательности координатных функций
,,,,
n
ϕϕϕ
21
существен-
но влияет на степень сложности вычислений, и от удачного выбора координатной си-
стемы функций зависит эффективность применения метода Ритца.
Если граничные условия линейны и однородны, например вида
0
21
==
)()( xyxy
или
53

,)()(
,)()(
0
0
222212
121111
=
′
+
=
′
+
xyxy
xyxy
αα
αα
где
ij
α
−=
),( 21j
постоянные коэффициенты, то координатные функции следу-
ет выбирать так, чтобы они удовлетворяли этим граничным условиям. В этом случае
семейство
∑
=
=
n
i
i
xCxny
1
)(),(
ϕ
при любых
i
C
также удовлетворяет тем же граничным условиям.
Например, если граничные условия
0
21
==
)()( xyxy
, то в качестве координат-
ных функций можно выбрать семейство функций
)())(()( xxxxxx
ii
ψϕ
21
−−=
,
где
−
)(x
i
ψ
непрерывные функции, или
)(
)(
sin)(
2
1
xx
xxk
x
k
−
−
=
π
ϕ
),,(
21
=
k
.
Если граничные условия неоднородны, например
11
axy
=
)(
,
22
axy
=
)(
, где
хотя бы одно из чисел
1
a
и
2
a
отлично от нуля, то предпочтительнее выбирать систе-
му координатных функций в виде (11.7), т.е.
∑
=
+=
n
i
ii
xCxxny
1
0
)()(),(
ϕϕ
,
где
)(x
0
ϕ
удовлетворяет заданным граничным условиям
110
ax
=
)(
ϕ
,
220
ax
=
)(
ϕ
, а остальные функции
−
)(x
i
ϕ
однородным граничным условиям
0
21
==
)()( xx
ii
ϕϕ
. Такой выбор координатных функций обеспечивает при любых
i
C
выполнение заданных граничных условий функциями
),( xny
. В качестве приме-
ра выбора функции
)(x
0
ϕ
можно предложить линейную функцию вида
11
12
12
0
axx
xx
aa
x
+−
−
−
=
)()(
ϕ
.
Недостаток метода Ритца заключается в сложности решения в общем случае си-
стемы уравнений (11.8), т.е.
),,,( ni
С
i
21 0
Ф
==
∂
∂
.
В частном случае исследования экстремума квадратичного относительно неиз-
вестной функции и её производных функционала решение задачи методом Ритца зна-
54
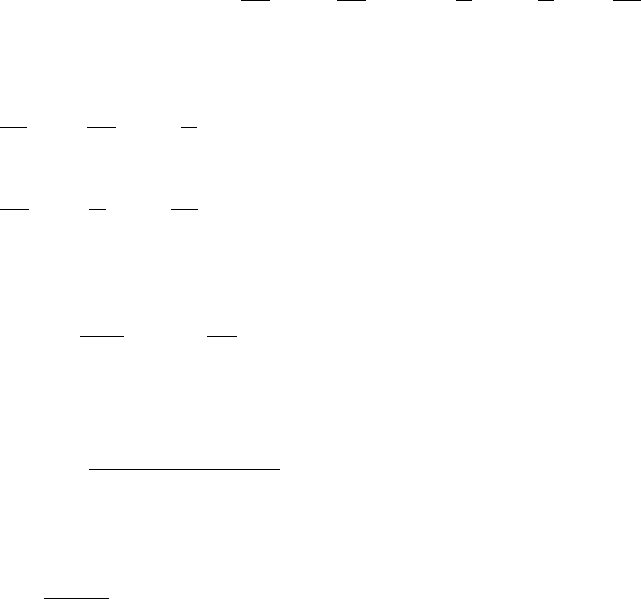
чительно упрощается, так как в этом случае уравнения (11.8) линейны относительно
i
С
.
Вычислительные аспекты метода Ритца можно продемонстрировать на следую-
щем примере.
Требуется минимизировать функционал
( )
∫
′
++
1
0
22
2 dxyxyy
,
010
==
)()( yy
.
Выбираем систему координатных функций в виде
0
0
=
)(x
ϕ
,
xxx
−=
2
1
)(
ϕ
,
,)(
23
2
xxx
−=
ϕ
,
,)(
nn
n
xxx
−=
+
1
ϕ
Примем
2
=
n
, тогда имеем
)()(),(
23
2
2
1
2 xxCxxCxy
−+−=
,
)()(),( xxCxCxy 23122
2
21
−+−=
′
,
21
2
221
2
121
10
1
6
1
7
1
30
11
30
11
Ф(2 CCCCCCCCxyI
−−++==
),)],([
.
Из условия (11.8) получим систему линейных алгебраических уравнений
6
1
30
11
15
11
21
=+
СС
,
10
1
7
2
30
11
21
=+
СС
,
решение которой даёт
43
7
473
69
21
==
CС ,
.
Следовательно, приближенное решение вариационной задачи запишем в виде
473
69877
2
23
xxx
xy
−−
=
),(
.
Для рассматриваемого примера известно точное решение вариационной задачи
( )
xy
xx
−−
−
=
−
1
2
.
Оценку точности приближенного решения можно получить сопоставлением с
точным решением из таблицы 11.1. По методу Ритца выбирается координатная систе-
ма функций
55
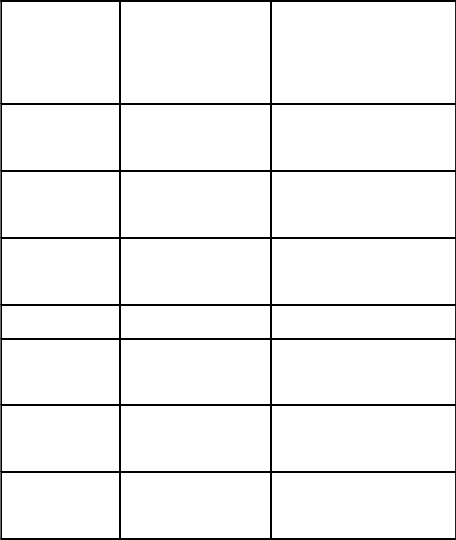
. ,,,( ,,,( ,,,( 911
21212211
),,),),).(
nmnn
xxxxxxxxx
ϕϕϕ
приближенное решение вариационной задачи ищется в виде
∑
=
=
m
k
nkkm
xxxCz
1
21
,,,( 1011 )).(
ϕ
,
где
−
k
C
постоянные коэффициенты.
По методу Канторовича также выбирается система координатных функций
(11.9), но приближенное решение ищется в виде
∑
=
=
m
k
nkikm
xxxxCz
1
21
,,,( )( 1111 )).(
ϕ
,
где коэффициенты
−
)(
ik
xC
неизвестные функции одной из независимых пере-
менных.
Исходный функционал в классе функций вида (11.11) превращается в функцио-
нал
))(,),(),((
~
imii
xCxCxCI
21
который зависит от
m
функций одной
независимой переменной. Функции
)(,),(),(
imii
xCxCxC
21
выбираются так,
чтобы функционал
I
~
достигал экстремума.
Если перейти к пределу при
∞→
m
, то при
выполнении некоторых условия можно по-
лучить точное решение. Если не выполнять
предельного перехода, то получаем при-
ближенное решение, более точное, чем при
применении метода Ритца с теми же коор-
динатными функциями и с тем же числом
членов.
Повышение точности при методе Кан-
торовича вызвано тем, что класс функций
(11.11) с переменными коэффициентами
)(
ik
xС
шире класса функций (11.10) с по-
стоянными коэффициентами
k
С
и среди
функций вида (11.11) с переменными коэф-
фициентами можно подобрать функции с большей точностью, аппроксимирующие
решение вариационной задачи, чем среди функций (11.10) с постоянными коэффици-
ентами.
56
Таблица 11.1
x
y
(точное зна-
чение)
),( xy 2
(приближен-
ное значение)
0.0 0.000
0
0.0000
0.2 -
0.0278
-0.0285
0.4 -
0.0505
-0.0506
0.5 -0.566 -0.0568
0.6 -
0.0583
-0.0585
0.8 -
0.0444
-0.0442
1.0 0.000
0
0.0000

12.МЕТОДЫ РЕШЕНИЯ. МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА
Вариационные задачи на условный экстремум можно решать с помощью метода
неопределенных множителей Лагранжа, применение которого сводит исходную зада-
чу к задаче на безусловный экстремум.
Пусть, например, требуется исследовать на экстремум функционал
∫
′′′
=
1
0
212121
1212
x
x
nnn
dxyyyyyyxFyyyI ),,,,,,,,(),,,().(
при наличии условий
).;,,,(
),,,,().(
nmmi
yyyx
ni
<=
=
21
0 1312
21
ϕ
Вместо исходной задачи (12.12), (12.13) составляют исходный функционал
∫
∑
+=
=
1
0
1
1412
x
x
m
i
ii
dxxFI
ϕλ
)().(
*
,
где
−
)(x
i
λ
множители Лагранжа, который исследуется на безусловный экстремум.
Обозначив
∑
=
+=
m
i
ii
xFF
1
ϕλ
)(
*
,
составляют систему уравнений Эйлера для нового функционала (12.14)
),,,().(
**
njF
dx
d
F
jj
yy
21 0 1512
==−
′
и дополняют систему (12.15) уравнениями связей (12.13).
Число уравнений (12.13) и (12.15), равное
nm
+
, достаточно для определения
nm
+
неизвестных функций
n
yyy ,,,
21
и
m
λλλ
,,,
21
, а граничные условия
0
0
jj
yxy
=
)(
и
1
1
jj
yxy
=
)(
),,,( nj
21
=
, которые не должны противоречить урав-
нениям связей, дают возможность определить
n2
произвольных постоянных в общем
решении системы уравнений Эйлера.
Метод множителей Лагранжа применим и в тех случаях, когда уравнения связей
являются дифференциальными уравнениями
0
2121
=
′′′
),,,,,,,,(
nni
yyyyyyx
ϕ
),,,( mi
21
=
.

Проиллюстрируем применение метода множителей Лагранжа в частном случае
минимизации функционала
∫
′′
=
2
2121
1612
x
x
dtyyyytFI ),,,,().(
при условии
tx
=
1712 ).(
,
.),,( 0
21
=
yyt
ϕ
Необходимое условие функционала (12.17) определяется равенством нулю его
первой вариации
0 1812
1
0
22
2
11
1
=
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
=
∫
dt
y
F
dt
d
y
F
y
y
F
dt
d
y
F
yI
x
x
δδδ
).(
.
Наличие условия (12.17) определяет зависимость между
1
y
и
2
y
. Найдём вариа-
цию (12.17), тогда
0 1912
2
2
1
1
=
∂
∂
+
∂
∂
=
y
y
y
y
δ
ϕ
δ
ϕ
δ ϕ
).(
.
Умножим (12.19) на множитель Лагранжа
)(t
λ
и проинтегрируем выражение
(12.19)
0 2012
1
0
2
2
1
1
=
∂
∂
+
∂
∂
∫
x
x
dty
y
y
y
t
δ
ϕ
δ
ϕ
λ
)().(
.
Сложим (12.18) и (12.20):
0 2112
1
0
222
2
111
1
=
∂
∂
+
∂
∂
−
∂
∂
+
∂
∂
+
∂
∂
−
∂
∂
∫
x
x
dt
yy
F
dt
d
y
F
y
yy
F
dt
d
y
F
y
ϕ
λδ
ϕ
λδ
).(
.
Выберем множитель Лагранжа
λ
таким образом, чтобы подынтегральное выра-
жение в первых скобках (12.21) было равно нулю. Из этого следует, что произвольной
вариации
2
y
δ
подынтегральное выражение во вторых (12.21) также должно равняться
нулю. Тогда имеем уравнения Эйлера – Лагранжа
0
11
=
∂
∂
∂
−
∂
∂
y
F
ty
F
**
,
0
22
=
∂
∂
−
∂
∂
y
F
dt
d
y
F
**
,
где
λ ϕ
+=
FF
*
, которые решаются совместно с условиями (12.17).
58

Рассмотрим пример применения метода множителей Лагранжа. Задано диффе-
ренциальное уравнение системы
)(tu
=
θ
, которое описывает поворот космического
аппарата в свободном пространстве под действием управления
)(tu
. Требуется мини-
мизировать функционал
∫
=
2
0
2
2
1
dtI )(
θ
так, чтобы
10
==
)(t
θ
,
02
==
)(t
θ
,
10
==
)(t
θ
,
02
==
)(t
θ
.
Введём обозначение
)()( tty
θ
=
1
. Тогда дифференциальное уравнение системы
примет вид
21
yy
=
,
uy
=
2
.
Если применить метод множителей Лагранжа, рассматривая
)(tu
в качестве
переменной
3
y
, то задача сводится к минимизации функционала
( ) ( )
∫
−+−+=
2
0
22121
2
2
1
dtytutytyttuI )()()()()(
λλ
.
Уравнения Эйлера-Лагранжа для данного примера имеют вид
0
1
=
λ
,
)(t
12
λλ
−=
,
)()( ttu
2
λ
−=
.
Решение уравнения Эйлера-Лагранжа совместно с дифференциальными уравне-
ниями системы и с учётом заданных граничных условий определяет оптимальное
управление и оптимальные траектории системы в форме
2
7
3
−=
tu
;
1
4
7
2
1
23
1
++−=
ttty
;
1
2
7
2
3
2
2
+−=
tty
.
Методом множителей Лагранжа решаются задачи на условный экстремум в фор-
ме Лагранжа, Майера, Больца и изопериметрические задачи. В качестве примера
рассмотрим применение метода множителей Лагранжа в изопериметрической задаче.
Требуется найти экстремум функционала
59
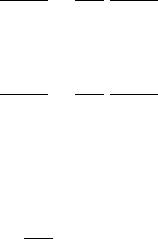
∫
′
=
1
0
11
2212
x
x
dxyyxFI ),,().(
при условии, что другой функционал
∫
′
=
1
0
22
x
x
dxyyxFI ),,(
сохраняет заданное значение
C
.
Сведём изопериметрическую задачу к общей задаче Лагранжа. Введя обозначе-
ние
∫
′
=
1
0
2
x
x
dxyyxFx ),,()(
ψ
,
получим
),,().( yyxF
′
=
′
2
2312
ψ
.
Теперь требуется найти функции
)(xy
и
)(x
ψ
, доставляющие экстремум функ-
ционалу (12.22) при условии (12.23). Составляем новый функционал
( )( )
dxFFI
x
x
∫
−
′
+=
1
0
21
2412
ψλ
*
).(
,
где
−
λ
множитель Лагранжа.
Уравнения Эйлера-Лагранжа для функционала (12.24) имеют вид
0
=
′
∂
∂
−
∂
∂
y
F
dx
d
y
F
**
,
0
=
′
∂
∂
−
∂
∂
ψψ
**
F
dx
dF
,
где
( )
21
FFF
−
′
+=
ψλ
*
. Из второго уравнения следует
0
=
λ
dx
d
или
const
=
λ
.
В изопериметрической задаче множитель Лагранжа является постоянным чис-
лом.
60
